(1 point) Suppose f(x,y) = xy(1 - 4x - 2y). f(x,y) has 4 critical points. List them in increasing lexographic order. By that we mean that (x,y) comes before (z, w) if x
Answers
Increasing lexicographic order: (0, 0), (0, 1/2), (1/4, 0), (1/4, 1/2)).Thus, the increasing lexicographic order of the critical points of the function f(x,y) = xy(1 - 4x - 2y) are (0, 0), (0, 1/2), (1/4, 0), and (1/4, 1/2).
lexicographic order: (0, 0), (0, 1/2), (1/4, 0), (1/4, 1/2)).Thus, the increasing lexicographic order of the critical points of the function f(x,y) = xy(1 - 4x - 2y) are (0, 0), (0, 1/2), (1/4, 0), and (1/4, 1/2).
Suppose that f(x,y) = xy(1 - 4x - 2y). f(x,y) has 4 critical points.
Let's discuss what are critical points and how we can determine them,A critical point is a point on the graph where the derivative changes its sign.
In other words, the derivative either changes from negative to positive or from positive to negative. A critical point is also known as a stationary point or a turning point
To determine the critical points, we need to find the derivative of the given function and set it equal to zero.The given function is\(f(x,y) = xy(1 - 4x - 2y).\)
Let's find the partial derivative of f with respect to \(x:f_x(x,y) = y(1 - 4x - 2y) - 4xy = (1-2y)(1-4x)y.\) (1)
Now, find the partial derivative of f with respect to y:f_y(x,y) = x(1 - 4x - 2y) - 2xy = (1-2x)(1-2y)x. (2)
To find the critical points, we need to set both partial derivatives (1) and (2) equal to zero.
(1-2y)(1-4x) = 0 and (1-2x)(1-2y) = 0.
Solving both equations separately, we have the following critical points:(1/4, 1/2), (1/4, 0), (0, 1/2), and (0, 0).
for such more questions on lexicographic order
https://brainly.com/question/22852607
#SPJ11
Related Questions
guys I need help
please help me

Answers
could yu solve this in the pic

Answers
The areas meet the Pythagorean's theorem, with that we conclude that the area of square 3 is 13 square centimeters.
What is the area of the square 3?If you look at the shape between the 3 squares, you can see that we have a right triangle.
Then, by Pythagorean's theorem we can conclude that the area of square 2 plus the area of square 3 must be equal to the area of the square 1.
Then we can write:
Area 2 + Area 3 = Area 1.
We know that:
area 1 = 25 cm²
area 2 = 12 cm²
area 3 = x
then we can write:
x + 12cm² = 25cm²
x = 25cm² - 12cm² = 13cm²
So the correct option is D.
Learn more about Pythagorean's theorem at:
https://brainly.com/question/343682
#SPJ1
Suppose you are going to conduct a two tail test concerning the population mean. Suppose that you do not know what the population standard deviation is and that you have a sample of 55 observations. If you are going to conduct this test at the. 01 level of significance what is the critical value? be sure to enter a positive number and answer to four decimal places.
Answers
The critical value for this two-tailed test is 2.6759.
To conduct a two-tailed test at the 0.01 level of significance with a sample of 55 observations, we use the t-distribution because the population standard deviation is unknown. The critical value is determined by dividing the significance level (0.01) by 2 to account for both tails of the distribution. This gives an alpha level of 0.005. Using the degrees of freedom for a sample of size 55 (54 degrees of freedom), we find the corresponding critical value from a t-distribution table or calculator. In this case, the critical value is approximately 2.6759 when rounded to four decimal places.Since the population standard deviation is unknown, we'll use the t-distribution instead of the standard normal distribution. The degrees of freedom for a sample of size 55 is 54. Using a t-distribution table or a statistical calculator, the critical value for an alpha level of 0.005 and 54 degrees of freedom is approximately 2.6759 (rounded to four decimal places).
learn more about two-tailed tests here:
https://brainly.com/question/8170655
#SPJ11
Find Mx, My, and (x, y) for the laminas of uniform density rho bounded by the graphs of the equations. y=8x, y = 0, x = 8 Mx = (x, y)
Answers
To find Mx, My, and (x, y) for the laminas of uniform density rho bounded by the graphs of the equations y = 8x, y = 0, and x = 8, we need to calculate the moments of the laminas.
Mx represents the moment about the y-axis, My represents the moment about the x-axis, and (x, y) represents the centroid of the laminas.
To calculate Mx, we integrate the product of the density rho, the y-coordinate squared, and the differential area element dA:
Mx = ∫∫ y^2 * rho * dA
Since the laminas have uniform density, rho is constant, and we can simplify the equation:
Mx = rho * ∫∫ y^2 * dA
To calculate My, we integrate the product of the density rho, the x-coordinate squared, and the differential area element dA:
My = ∫∫ x^2 * rho * dA
Again, since the laminas have uniform density, rho is constant, and we can simplify the equation:
My = rho * ∫∫ x^2 * dA
To find the centroid (x, y), we divide the moments Mx and My by the total mass (m) of the laminas:
x = Mx / m
y = My / m
To calculate these values, we need to set up the appropriate double integrals over the region bounded by the given equations.
Know more about integrate here;
https://brainly.com/question/31744185
#SPJ11
The functions f(x)=−34x+214 and g(x)=(12)x+1 are shown in the graph. What are the solutions to −34x+214=(12)x+1? Select each correct answer.

Answers
The graphs cross at x=-1 and x=1. Those are the solutions to to the equation
How to explain the graphWe know that, If two functions are equal then there solution is the intersection point of the curves.
When we determine the graph the intersection points are (0,2) and (1,1.25).
The values of x of the intersection points are the solutions of the system
Using a graphing tool, there are two intersection points and therefore the solutions are x = -1 and x [ 1.
Learn more about graph on
https://brainly.com/question/8658188
#SPJ1
can yall help me with this i am actually crying

Answers
Answer:
To find out, we need to subtract the distance Carmen has already gone from the total distance to her school:
5 2/3 - 1 1/5
We need to find a common denominator of 15:
5 10/15 - 1 3/15
Now we can subtract the whole numbers and the fractions separately:
4 - 7/15
To turn the fraction into a mixed number, we need to divide the numerator (7) by the denominator (15):
7 ÷ 15 = 0 remainder 7
Then we can write the mixed number:
4 7/15
Therefore, Carmen still has to jog 4 7/15 miles to get to school.
Step-by-step explanation:
DE D 5х - 12 Е Зх 3х - 4 4 F

Answers
EXPLANATION
We have an equilateral triangle because the 3 angles are congruent as shown in the picture and all legs are congruent:
So, 5x-12 = 3x - 4
Adding +12 to both sides:
5x - 12 + 12 = 3x - 4 + 12
Simplifying:
5x = 3x + 8
Subtracting both sides by -3x:
5x - 3x = 3x - 3x + 8
Simplifying:
2x = 8
Dividing both sides by 2:
x = 8/2
Simplifying:
x=4
Now, replacing in any equation, as 5x - 12:
5*(4) - 12= 8
In conclusion, all the legs are congruent and equal to 8.
Answer: DE= 8
By using sum or difference formulas, cos(-a) can be written as OA. - sin(x) B. - cos(x) Oc.cos(x) D. sin(x) OE. All of the above OF. None of the above By using sum or difference formulas, cos(-a) can be written as OA. - sin(x) B. - cos(x) Oc.cos(x) D. sin(x) OE. All of the above OF. None of the above By using sum or difference formulas, cos(-a) can be written as OA. - sin(x) B. - cos(x) Oc.cos(x) D. sin(x) OE. All of the above OF. None of the above
Answers
By using sum or difference formulas, cos(-a) can be written as - cos(a). Explanation: We know that cosine is an even function of x, therefore,\(cos(-x) = cos(x)\) .Then, by using the identity \(cos(a - b) = cos(a) cos(b) + sin(a) sin(b)\), we can say that:\(cos(a - a) = cos²(a) + sin²(a).\)
This simplifies to:\(cos(0) = cos²(a) + sin²(a)cos(0) = 1So, cos(a)² + sin(a)² = 1Or, cos²(a) = 1 - sin²\)(a)Similarly,\(cos(-a)² = 1 - sin²(-a)\) Since cosine is an even function, \(cos(-a) = cos(a)\) Therefore, \(cos(-a)² = cos²(a) = 1 - sin²(a)cos(-a) = ±sqrt(1 - sin²(a))'.\)
This is the general formula for cos(-a), which can be written as a combination of sine and cosine. Since cosine is an even function, the negative sign can be written inside the square root: \(cos(-a) = ±sqrt(1 - sin²(a)) = ±sqrt(sin²(a) - 1) = -cos\).
To know more about sum visit:
https://brainly.com/question/31538098
#SPJ11
could someone help with this

Answers
∠1 = 26°
∠2 = 154°
∠3 = 26°
∠4 = 26°
∠5 = 154°
∠6 = 154°
∠7 = 26°
Step-by-step explanation:
So, we have two parallel lines cut by a transversal (C).
Vertical angles are always equal.
∠2 = 154° (vertical angles)
Linear pair make up 180°.
∠1 = 180° - 154° = 26° (linear pair)
∠1 = ∠3 = 26° (vertical angles)
Corresponding angles are always equal.
∠5 = 154° (corresponding angles)
∠5 = ∠6 = 154° (vertical angles)
Alternate Interior angles are always equal.
∠3 = ∠4 = 26° (alternate interior angles)
∠4 = ∠7 = 26° (vertical angles)
Consider a line process with 3 processing stages. The production requires each unit to go through Stage A through Stage C in sequence. The characteristics of the Stages are given below: Stage A B C Unit processing time(minutes) 1 2 3 Number of machines 1 1 2 Machine availability 90% 100% 100% Process yield at stage 100% 100% 100% Determine the system capacity. Which stage is the bottleneck? What is the utilization of Stage 3.
Answers
The system capacity is 2 units per minute, the bottleneck stage is Stage A, and the utilization of Stage 3 is 100%.
A line process has three processing stages with the characteristics given below:
Stage A B C Unit processing time(minutes) 1 2 3 Number of machines 1 1 2 Machine availability 90% 100% 100% Process yield at stage 100% 100% 100%
To determine the system capacity and the bottleneck stage and utilization of Stage 3:
The system capacity is calculated by the product of the processing capacity of each stage:
1 x 1 x 2 = 2 units per minute
The bottleneck stage is the stage with the lowest capacity and it is Stage A. Therefore, Stage A has the lowest capacity and determines the system capacity.The utilization of Stage 3 can be calculated as the processing time per unit divided by the available time per unit:
Process time per unit = 1 + 2 + 3 = 6 minutes per unit
Available time per unit = 90% x 100% x 100% = 0.9 x 1 x 1 = 0.9 minutes per unit
The utilization of Stage 3 is, therefore, (6/0.9) x 100% = 666.67%.
However, utilization cannot be greater than 100%, so the actual utilization of Stage 3 is 100%.
Hence, the system capacity is 2 units per minute, the bottleneck stage is Stage A, and the utilization of Stage 3 is 100%.
Know more about bottleneck here,
https://brainly.com/question/32590341
#SPJ11
{c} Factorise: c² - 8c
Answers
Answer:
c (c - 8)
Step-by-step explanation:
c² - 8c
First, you have to find the GCF
The Greatest Common Factor is the factor that all have in common. Here the GCF is c
So, we factor c out and has left (c - 8)
So, our equation is
c (c - 8)
Solve: 6-x =4(5+x)-4

Answers
Answer:
option A , x=-2
Step-by-step explanation:
6-x =4(5+x)-4
6 - x = 4 × 5 + 4 × x - 4
6 - x = 20 + 4x - 4
6 - x = 4x + 16
-x - 4x = 16 - 6
-5x = 10
x = 10/-5
x = -2
therefore, option A is the correct option
hope it helps you
Answer:
First, finish the brackets
6-x=20+4x-4
Collect like terms
-x-4x=20-4-6
Solve
-3x=10
x=-10/3
x=-3.33333333333 Or x≅3.34
Step-by-step explanation:
Please give me brainliest
Out of 300 students in a class, 60 percent students study physics, 35 percent students study chemistry and 20 percent do not study both of the subjects. how many students study both subjects
Answers
22 students study both subjects.
What is Venn diagram in math ?
In a Venn diagram, sets are represented by shapes; usually circles or ovals. The elements of a set are labeled within the circle.N=55,n(M)=23,n(P)=24,n(C)=19,n(M∩P)=12,n(P∩C)=7,n(M∩C)=9,n(M∩P∩C)=4
Now, number of students who studying only Mathematics
n(M∩P)∩C =n(M)−n(M∩P)−n(M∩C)+n(M∩P∩C) (by Venn diagram) diagram=23−9−12+4=6
number of students who studying only Physics
n(P∩M )∩C =n(P)−n(P∩M)−n(P∩C)+n(P∩M∩C) (by Venn diagram)
=24−12−7+4=9
Now, number of students who studying only Chemistry
n(C∩M )∩P =n(C)−n(C∩M)−n(C∩P)+n(M∩P∩C) (by Venn diagram)
=19−9−7+4=7
So, how many students study only one of the three disciplines in detail 6+9+7=22
Learn more about venn diagram
brainly.com/question/14344003
#SPJ4
Write an equation in slope intercept form with the given information.
Goes through points (-2,-5) and (3,5)
Answers
Answer:
infinity 2 is the slope for these point .
Step-by-step explanation:
given points are
(-2,-5) and (3,5)
comparison to
(x1,y1) and (x2,y2)
here ,
\(slope = \frac{y2 - y1}{x2 - x1} \)
slope= 5-(-5)/3-(-2)
slope =10/5
slope=2
glad to help you this may help you :)
In the figure below, m4=96°. Find mZ1, mZ2, and mZ 3.

Answers
The answer is m∠1 = 84°
Step-by-step explanation:
m∠4 = m∠2 so m∠2 = 96°
m∠1 + m∠2 = 360 - m∠4 - m∠2
m∠1 + m∠2 = 360 - 96 - 96
m∠1 + m∠2 = 168
m∠1 = 168/2
m∠1 = 84°
What is 60% of 150? Please answer.
Answers
Answer:
90
Step-by-step explanation:
Answer:
Your answer is 90
Step-by-step explanation:
You take 150 and multiply it by .6 to get 90
What is BD? imported image attached
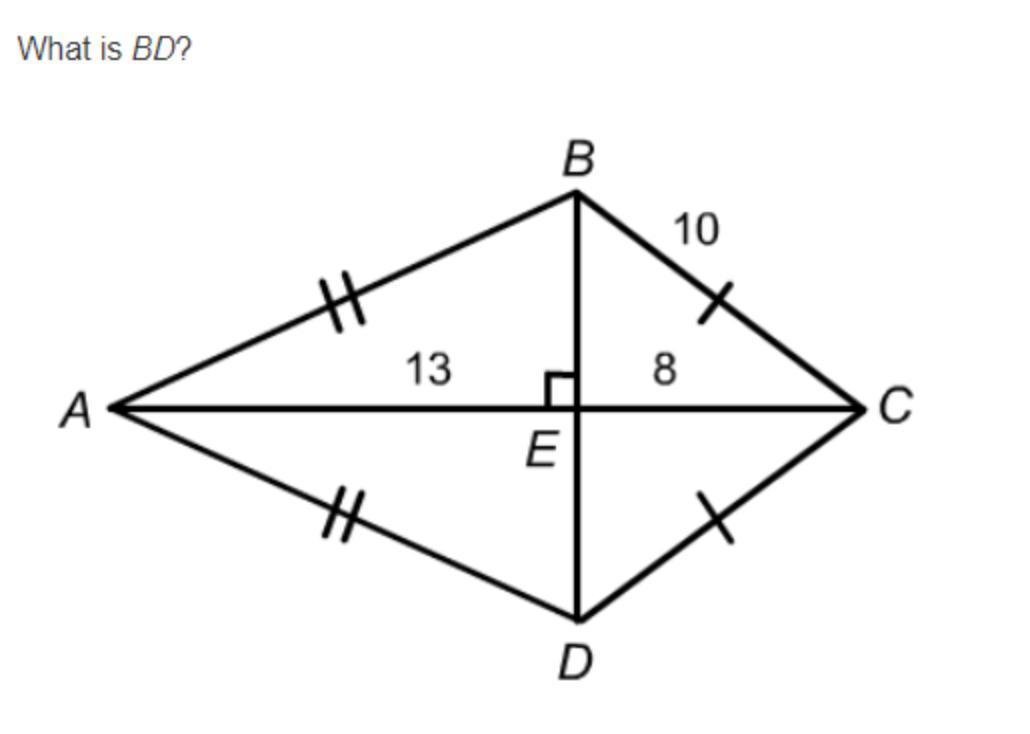
Answers
Answer:
12
Step-by-step explanation:
i know that
I did this so yeah
The dimension of the row space of a 3 x 3 matrix A is 2. (a) What is the dimension of the column space of A? (b) What is the rank of A? (c) What is the nullity of A? (d) What is the dimension of the solution space of the homogeneous system Ax = 0?
Answers
a) the dimension of its column space is also 2. b) the rank of A is 2. c) the nullity of matrix A is 1. d) the dimension of the solution space of the homogeneous system \(A_x = 0\) is also 1.
(a) The dimension of the row space of a matrix is equal to the dimension of its column space. So, if the dimension of the row space of matrix A is 2, then the dimension of its column space is also 2.
(b) The rank of a matrix is defined as the maximum number of linearly independent rows or columns in the matrix. Since the dimension of the row space of matrix A is 2, the rank of A is also 2.
(c) The nullity of a matrix is defined as the dimension of the null space, which is the set of all solutions to the homogeneous equation Ax = 0. In this case, the matrix A is a 3 x 3 matrix, so the nullity can be calculated using the formula:
nullity = number of columns - rank
nullity = 3 - 2 = 1
Therefore, the nullity of matrix A is 1.
(d) The dimension of the solution space of the homogeneous system Ax = 0 is equal to the nullity of the matrix A. In this case, we have already determined that the nullity of matrix A is 1. Therefore, the dimension of the solution space of the homogeneous system \(A_x = 0\) is also 1.
Know more about matrix here:
brainly.com/question/24079385
#SPJ4
9.60 how large a sample is needed if we wish to be 99onfident that our sample proportion in exercise 9.51 will be within 0.05 of the true proportion of homes in the city that are heated by oil?
Answers
The sample size needed to obtain a 99% confidence interval with a margin of error of 0.05 for the true proportion of homes in the city that are heated by oil is 666.
To calculate the required sample size, we need to use the formula n = \((z^2 * p * q) / e^2\), where z is the z-score for the desired confidence level (2.58 for 99% confidence), p is the estimated proportion of homes heated by oil, q is 1-p, and e is the desired margin of error (0.05).
Using the information given in the question, we can estimate p as 0.5 (assuming equal probability of homes being heated by oil or other means) and q as 0.5. Plugging these values into the formula, we get n = \((2.58^2 * 0.5 * 0.5) / 0.05^2\), which simplifies to n = 665.64. Therefore, we would need a sample size of at least 666 homes to obtain a 99% confidence interval with a margin of error of 0.05 for the true proportion of homes in the city that are heated by oil.
Thus, the answer is 666.
You can learn more about sample size at
https://brainly.com/question/28583871
#SPJ11
[8x(7 divided by 7)] ^2
Answers
Answer:
Step-by-step explanation:
[8 * (7÷7)]² = [8 * 1]²
= 8²
= 64
The operation in the inside parenthesis should be done first.
Fill in the missing pieces to solve for x:

Answers
Answer:
A: (x-4) squared
B: x+2
C: 9
D: 14
E: 7
F: 2
Step-by-step explanation:
A: This is because x^2 - 8x + 16 factored is (x-4) squared
B: Square root of something squared will remove the square root
C: Minus the variable x and 2 from the right side
D: Factor
E/F: These numbers make the right side become zero
Which graph represents the step function
f(x) = (x +1] ?
3
2
1
1
2
-2 -1
2
2
1
O 17
1
1
-3 -2 -1
3-2-11
2 3
20
-2
I need helppp
![Which graph represents the step functionf(x) = (x +1] ?32112-2 -1221O 1711-3 -2 -13-2-112 320-2I need](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/mJ0QKCrwhRqgiWqDWvbwvgTKIyVLCizU.png)
Answers
1. K(x) = (3x)2 -x + 2 -x + 1
k(x) = g(x) ∘ h(x)
2. K(x) = 2 ^3x + 2
k(x) = g(x) × h(x)
3. K(x) = 2^x - 3x - 2
k(x) = h(x) ÷ g(x))
4. K(x) = 3(2 x) + 2
k(x) = h(x) ∘ g(x)
5. K(x) = 2^x + 3x + 2
k(x) = g(x) - h(x)
6. K(x) = 2^x(3x + 2)
k(x) = g(x) + h(x)
Evan saved $30 on a new TV. If the percent of discount was 20%, how much money did the
TV originally cost?
Answers
Answer:
$150
Step-by-step explanation:
we can make a ratio
20/100=30/x
cross multiple
20x=30(100)
20x=3,000
/20 /20
x=150 hopes this helps
Need help ASAP! Please show work if you can,

Answers
12+7-(-2)=
12-7-2=
21
Rotate the shape 90 degreese clockwise about (3,1)

Answers
Its going to be on quadrants 1 and 4.
PLEASE HELP!!! AND HURRY, I HAVE 15 MIN TO FINISH!!!!!
Which best describes this inheritance pattern?
The diagram shows the results when two parents are
crossed. The letters represent alleles for a trait that is
controlled by three different genes.
o multiple allele because a trait is controlled by three
different genes
polygenic because the offspring have alleles from
both parents
multiple allele because the offspring have alleles
from both parents
polygenic because a trait is controlled by three
different genes
Answers
Answer:its b i think
Step-by-step explanation:
Answer: D, polygenis because a trait is controlled by three different genes.
Step-by-step explanation: I got 100 of the test ^^
HELPPP
Ray AT bisects ∠MAR. If m∠MAT = (4x − 5)° and m∠RAT = (2x + 7)°, what is the m∠MAR.
6°
15°
19°
38°
Answers
m∠MAR is 68°. Answer: 38°.
What is the angle bisectors?
In geometry, an angle bisector is a line or ray that divides an angle into two equal parts. More formally, given an angle ABC, an angle bisector is a line or ray AD such that it divides the angle ABC into two equal angles: ∠ABD ≅ ∠CBD.
Since ray AT bisects ∠MAR, we know that m∠MAT + m∠RAT = m∠MAR.
Substituting the given values, we get:
(4x - 5)° + (2x + 7)° = m∠MAR
Simplifying and solving for x, we get:
6x + 2° = m∠MAR
Now, we know that the sum of the angles in a triangle is 180°. So:
m∠MAT + m∠RAT + m∠MAR = 180°
Substituting the given values and the expression we found for m∠MAR, we get:
(4x - 5)° + (2x + 7)° + (6x + 2°) = 180°
Simplifying and solving for x, we get:
x = 11°
Finally, we can substitute x = 11° into the expression we found for m∠MAR:
6x + 2° = 6(11°) + 2° = 68°
Hence, m∠MAR is 68°. Answer: 38°.
To learn more about angle bisectors, Visit
https://brainly.com/question/24334771
#SPJ1
What is the missing reason in step 6? SSS congruency theorem CPCTC definition of a parallelogram opposite sides in a parallelogram are congruent.
Answers
For the two parallelogram to be congruent, their corresponding sides must be equal
Congruent figuresTwo figures are said to be congruent if they are of the same shape and their corresponding sides and angles are congruent to each other. The SSS congruency theorem states that two figures are congruent of all their sides are congruent.
For the two parallelogram to be congruent, their corresponding sides must be equal
Find out more on similar figures at: https://brainly.com/question/26173060
Answer: CPCTC
Step-by-step explanation:
edge 23
In the picture below and pls show steps or explain

Answers
So 5 times that is:
5(x+4)
Find the value of X and prove the following

Answers
The value of the variable x can be determined using the circle theorem to
determine the angle formed by x.
The correct responses are;
(1) x = 30°(2) x = 100°(3) x = 60°Reasons:
(1) From circle theorem, we have;
Equal chords subtends equal arcs and vice versaEqual chords subtend equal angles at the center of a circleTherefore;
Angle subtended by \(\displaystyle \widehat {AB}\) at center = Angle subtended by \(\widehat {BC}\) at the center;
Angle at the center = 2 × Angle at the circumferenceTherefore;
Angle subtended by \(\displaystyle \widehat {AB}\) at the circumference = Angle subtended by \(\mathbf{\widehat {BC}}\) at the circumference
Which gives;
x = 30°(2) \(\displaystyle \widehat {AB} = \mathbf{\widehat {CD}}\) given
Angle subtended by arc \(\widehat {CD}\) at the center = x
Equal arcs subtend equal angles at the center of a circle.
Therefore;
Angle subtended by arc \(\mathbf{\widehat {AB}}\) at the center = x
Angle at center = 2 × angle at circumference
Therefore;
x = 2 × 50° = 100°
x = 100°
(3) \(\displaystyle \widehat {AC} = \mathbf{ 3 \times \widehat {AB}}\) given
By definition, we have;
Angle subtended by \(\widehat {AC}\) at the center = 3 × Angle subtended by \(\widehat {AB}\) at the center
According to circle theorem, we have;
Angle at the center = 2 × Angle at the circumference
Let y represent the angle subtended at the circumference by \(\widehat {AB}\), we have;
y = 20°
\(\widehat {AB}\) = 2·y
\(\widehat {AC}\) = 3 × \(\widehat {AB}\) = 3 × 2·y = 6·y
Therefore;
\(\widehat {AC}\) = 6 × 20° = 120°
\(\widehat {AC}\) = 120°
\(\widehat {AC}\) = 2·x
Therefore;
2·x = 120°
\(\displaystyle x = \frac{120^{\circ}}{2} = \mathbf{ 60^{\circ}}\)
x = 60°
Learn more circle theorems here:
https://brainly.com/question/16879446