Answers
Answer:
D :3 -Your friend, Bill Cipher
Step-by-step explanation:
Answer:
sqrt of 65, bc 8 squared is 64
Related Questions
help me, please cause I'm stuck

Answers
Answer:4.03 x 10^4
Step-by-step explanation:
The table shows the amount of flour
used to make waffles. What is the unit
rate for the amount of flour per waffle?

Answers
Answer:
⅛ cups per waffle
Step-by-step explanation:
conduct the appropriate hypothesis test and compute the p-value. sunshine air has determined that their no-show rate for passengers booked on a flight is 6%. the airline has recently increased the cost of its travel insurance and and suspects the no-show rate for passengers will decrease. a random sample of 380 reservations resulted in 18 no-shows. at the 0.10 significance level, is there strong enough sample evidence to suggest that the no-show rate in less than 6%?
Answers
The p-value is 0.15 which is greater than the significance value 0.10 so null hypothesis cannot be rejected at 10% significance level , we do not have enough evidences to state that no- show rate is less than 6%.
As given in the question,
Null hypothesis : No show rate for passengers booked on given flight is 6%
Alternative hypothesis: No show rate for passengers booked on given flight is less than the 6%
P = 6%
= 0.06
1 - P = 1 - 0.06
= 0.94
random sample size 'n' = 380
no shows = 18
Sample proportion 'p' = 18/ 380
= 0.047
Now , z test statistic value :
z = (p - P)/ √P (1- P)/n
= (0.047 - 0.06)/√0.06( 0.94)/380
= -0.013 /0.012
= -1.083
p-value = 0.2788 ( using table)
0.2788 > 0.10
p-value is greater than significance value 0.10
Do not reject null hypothesis at 10% level of significance.
Therefore, as p-value is greater than significance value do not have enough evidences to state that no- show rate is less than 6%.
Learn more about p-value here
brainly.com/question/14790912
#SPJ4
WILL GIVE BRAINLIEST
Given the parent function g(x) = log2 x
What is the equation of the function shown
in the graph?

Answers
Answer:
To determine the equation of the function shown on the graph, we need to analyze its characteristics. From the graph, we can see that the function passes through the point (2, 0) and has a vertical asymptote at x = 1. This information allows us to conclude that the function is a transformation of the parent function g(x) = log2 x. Specifically, it appears to be a horizontal compression and a vertical translation.
To find the equation of the function, we can start by applying the horizontal compression. Let k be the compression factor, then the function can be written as f(x) = log2(kx). Next, we can apply the vertical translation by adding or subtracting a constant, let h be the vertical shift, then the equation becomes f(x) = log2(kx) + h.
To determine the values of k and h, we can use the point (2, 0) and the fact that the vertical asymptote is at x = 1. Setting k = 1/2 since 2k = 1 (corresponding to a horizontal compression by a factor of 1/2), we can find h by substituting the point (2,0) into the equation and solving for h:
0 = log2(1) + h
h = 0
Therefore, the equation of the function shown on the graph is f(x) = log2(1/2 x), which can also be written as f(x) = log2(x) - 1.
Answer:
log2 (x - 3) - 2
Step-by-step explanation:
When x = 4
log2 of (4 - 3) - 2
= log2 1 - 2
= 0 - 2
So we have the point
(4, -2)
and when x = 7
we have y = log2(7-3) - 2
= log2 4 - 2
= 2-2
= 0
- so we have the poin7 (7,0)
Solve −6x+6−7=2x+8 for x. How would I solve this?
Answers
Answer:
Step-by-step explanation:
−6x+6−7=2x+8
-1-8=2x+6x
8x=-9
x= -\(\frac{9}{8}\)
helppp me pleaseeeeeeeeeeeeeeeeeeeeee

Answers
Answer:
1
----
7
Step-by-step explanation:
1 2x3 4x + 7x²+7
x² + 2x-1
DIVIDE

Answers
Answer:I think its 2×-3
Step-by-step explanation:Hope it helps kiddo
standard form of y=6(x-2)^2-3
Answers
y = 6(x - 2)² - 3
y = 6(x - 2)(x - 2) - 3
y = 6(x² - 2x - 2x + 4) - 3
y = 6(x² - 4x + 4) - 3
y = 6x² - 24x + 24 - 3
y = 6x² - 24x + 21
The complement of an event A, denoted by AC, within the sample space S, is the event consisting of all outcomes of A that are not in S. (true/false)
Answers
False. The complement of an event A, denoted by A', is the event consisting of all outcomes in the sample space S that are not in A.
In probability theory, a sample space S represents the set of all possible outcomes of an experiment or random phenomenon. An event A is a subset of the sample space S, representing a specific outcome or a combination of outcomes of interest.
The complement of event A, denoted by A', includes all the outcomes in the sample space S that are not part of event A. In other words, A' consists of all outcomes that do not satisfy the conditions for event A to occur.
For example, let's consider rolling a fair six-sided die. The sample space S consists of the numbers {1, 2, 3, 4, 5, 6}. Now, let event A be the event of rolling an odd number. In this case, A = {1, 3, 5}, and the complement of A, denoted by A', would be A' = {2, 4, 6}. A' includes all the outcomes that are not odd numbers.
It's important to note that the complement of an event A and the event itself together cover the entire sample space S. In other words, A and A' are mutually exclusive and exhaustive, meaning that any outcome must either be in A or in A'.
So, in summary, the complement of an event A is the set of all outcomes in the sample space S that do not belong to A.
To know more about probability theory refer here:
https://brainly.com/question/31469353
#SPJ11
6 apples to 2 mangoes
Answers
Answer:
6:2
Step-by-step explanation:
Answer:6:2 I hope this is helpful
Step-by-step explanation:
6 apples to 2 mangos is 6:2
PLEASE HELP !! Which of the following is the midpoint of a line segment with endpoints (-2,-4) and (6,8)? (4,6) or (4,4) or (2,2) or (2,4)
Answers
Answer:
The answer is (2 , 2)Step-by-step explanation:
The midpoint M of a line segment with two endpoints can be found using the formula
\(M = ( \frac{x1 + x2}{2} , \: \frac{y1 + y2}{2} )\)
where
(x1 , y1) and (x2 , y2) are the points
From the question
The endpoints are (-2,-4) and (6,8)
The midpoint is
\(M = ( \frac{ - 2 + 6}{2} , \frac{ - 4 +8 }{2} ) \\ = ( \frac{4}{2} , \frac{ 4 }{2} )\)
We have the final answer as
M = ( 2 , 2)Hope this helps you
A sample of 225 elements from a population with a standard deviation of 75 is selected. The sample mean is 180. The 95% confidence interval for is a. 105.0 to 225.0 b. 175.0 to 185.0 c. 100.0 to 200.0 d. 170.2 to 189 .8
Answers
95% confidence interval for the population mean is 170.2 to 189.8, option d is correct.
Explain indetail about why the option d is correct?We are given the following information:
- Sample size (n) = 225
- Standard deviation (σ) = 75
- Sample mean (x) = 180
- Confidence level = 95%
We need to calculate the 95% confidence interval for the population mean (μ). To do this, we will use the formula:
Confidence interval = x ± (z × σ/√n)
First, we need to find the z-score that corresponds to a 95% confidence level. For a 95% confidence interval, the z-score is 1.96 (you can find this value in a standard z-score table).
Now, we can plug in the values we have:
Confidence interval = 180 ± (1.96 × 75/√225)
Calculate the standard error (σ/√n):
Standard error = 75/√225 = 5
Now, calculate the margin of error (z * standard error):
Margin of error = 1.96 × 5 = 9.8
Finally, calculate the confidence interval:
Confidence interval = 180 ± 9.8 = (170.2, 189.8)
So, the 95% confidence interval for the population mean is 170.2 to 189.8, which corresponds to option d.
Learn more about confidence interval.
brainly.com/question/24131141
#SPJ11
Question 18
A wholesale grocery supplier shipped x2-pound blocks of cheese and y3-pound blocks of cheese to a caterer. The total weight of the cheese in the shipment was 44 pounds, and
the shipment consisted of 18 blocks of cheese. Which of the following systems of linear equations best represents this situation?
z+y=18
A
3z +2y=44
z+y=18
2x + 3y = 44
z+y=44
3z + 2y = 18
z+y=44
2z+3y=18
B
C
D
Imported (1)
The G
Answers
The system of linear equations that best represents the situation are:
z+y=18
3z +2y=44
What are the linear equations?In order to determine the values of the two types of cheese, two set of linear equations can be formed from the question. The equations have to be solved together using either the elimination , substitution or graphical methods.
To learn more about simultaneous equations, please check: https://brainly.com/question/25875552
#SPJ1
if a decision maker wishes to reduce the margin of error associated with a confidence interval estimate for a population mean, she can:
Answers
If a decision maker wishes to reduce the margin of error associated with a confidence interval estimate for a population mean, she can increase the sample size.
The margin of error refers to the statistic measurement that expresses the level of random sampling error in the outcomes of a survey. If the margin of error of the result is high, the confidence level would be low that a result reflects the census of the entire population. It indicated the difference between the actual and estimated results in a random survey sample. The margin of error is generally used in non-survey contexts to show observational error in reporting measured quantities. In order to minimize the margin of error associated with a confidence interval estimate for a population mean, the researchers can increase the sample size to capture the actual trend of the population more accurately.
Learn more about Margin of error:
https://brainly.com/question/24289590
#SPJ4
Resolve ax/a+x into an infinite series. Write the first 5 terms. Consider x as the variable. Then, use summation notation to create a formula for the infinite series
Answers
The infinite series ax/a+x can be expressed as a geometric series with the sum being a/a-x.
The infinite series for ax/a+x can be represented as a geometric series. The first five terms can be expressed as:
\(Term 1: ax/(a+x)\\Term 2: (ax)^2/(a+x)^2\\Term 3: (ax)^3/(a+x)^3\\Term 4: (ax)^4/(a+x)^4\\Term 5: (ax)^5/(a+x)^5\)
The infinite series can be expressed using summation notation as:
\(∑_(n=1)^∞ (ax)^n / (a+x)^n\)
Using the formula for a geometric series, the sum of the infinite series can be calculated as:
\(S = ax/(a+x) * 1/(1-ax/(a+x)) \\ = ax/(a+x) * (a+x)/(a-ax) \\ = ax/(a-ax) \\ = a/a-x\)
Therefore, the infinite series ax/a+x can be expressed as a geometric series with the sum being a/a-x.
Learn more about geometric series here:
https://brainly.com/question/23602882
#SPJ4
consider the following sequence at 87;84;81 which term will be the first negative term in the sequence
Answers
Answer:
"31st in the sequence"
87/3 = 29 .. 29 subtractions needed to get to zero
the 30th position in the sequence will be zero
the 31st is the first negative term
1 87
2 84
3 81
4 78
5 75
6 72
7 69
8 66
9 63
10 60
11 57
12 54
13 51
14 48
15 45
16 42
17 39
18 36
19 33
20 30
21 27
22 24
23 21
24 18
25 15
26 12
27 9
28 6
29 3
30 0
31 -3
Step-by-step explanation:
Please help! Will give brainliest!

Answers
After 10 weeks, there would be approximately 246 cell phone cases left.
To find the number of cell phone cases left after 10 weeks, we can substitute x = 10 into the equation and solve for C.
The given equation is:
log C = 2.84 - 0.042x
Substituting x = 10:
log C = 2.84 - 0.042(10)
log C = 2.84 - 0.42
log C = 2.42
To isolate C, we need to convert the equation from logarithmic form to exponential form.
In exponential form, the base of the logarithm becomes the base of the exponent. So, rewriting the equation in exponential form, we have:
\(C = 10^{(2.42)\)
Using a calculator, we find that \(10^{2.42\) is approximately 246.153.
Rounding to the nearest whole number, we have:
C ≈ 246
Therefore, after 10 weeks, there would be approximately 246 cell phone cases left.
Learn more about logarithmic form click;
https://brainly.com/question/29291192
#SPJ1
A square sandbox has sides of length 9 ft and a depth of 1 ft. If sand costs $5 / cubic foot, how much will it cost to fill the sandbox with sand?
Answers
The cost spent on fill the box with sand is 405$.
According to the statement
we have given a square sandbox with length 9 ft and depth of 1 ft.
and the rupees of sand per cubic ft is $5
then
Now, we have to find the volume of sandbox with the given length and depth.
So, for this purpose we use Volume formula
V = (a)^3
V = 9*9*1
V = 81 cubic feet
And the cost of sand per cubic feet is $5.
then
The cost of sand for 81 cubic per feet is calculate by multiplication formula then
Total cost of sand = 81*5
Total cost of sand = 405$
So, The cost spent on fill the box with sand is 405$.
Learn more about VOLUME here https://brainly.com/question/11408596
#SPJ4
Find the average value of the function f(x) = (x + 2) on the interval [0, 3].
![Find the average value of the function f(x) = (x + 2) on the interval [0, 3].](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/P5zl0SIYRlJ5Lz5JinzKHjLeHoS5AWmn.png)
Answers
The average value of the function f(x) = (x + 2) on the interval [0, 3] is 7/2.
Calculate the definite integral of the function over the interval [a, b], then divide it by the interval's length (b - a), in order to determine the average value of a function f(x) over the interval.
Given that the interval is [0, 3] and the function f(x) = (x + 2), we have:
= (1/3) × [1/2 x² + 2x] evaluated from x=0 to x=3
= (1/3) × [(1/2 × 3² + 2×3) - (1/20² + 20)]
= (1/3) × [(9/2 + 6) - 0]
= (1/3) × (21/2)
= 7/2
Therefore, the average value of the function f(x) = (x + 2) on the interval [0, 3] is 7/2.
Learn more about definite integral click;
https://brainly.com/question/30760284
#SPJ1
Find the solution(s) to the system of equations. Select all that apply.y=x^2 - 4y=-2х - 5ОА. (-1, -3)ОВ. (2, 0)ООООС. (-2, 0)оD. (-5, 0)
Answers
Given the system of equations:
• y = x² - 4
,• y = -2x - 5
Let's find the solution(s) to the system.
To find the solution, eliminate the equivalent sides and equate the expressions.
We have:
\(x^2-4=-2x-5\)Move all terms to the left and equate to zero.
Add 2x and 5 to both sides:
\(\begin{gathered} x^2+2x-4+5=-2x+2x-5+5 \\ \\ x^2+2x+1=0 \end{gathered}\)Factor the left side of the equation using the perfect square rule:
\(\begin{gathered} x^2+2x+1^2=0 \\ \\ x^2+2\cdot x\cdot1+1^2=0 \\ \\ (x+1)^2=0 \end{gathered}\)Solving further:
\(x+1=0\)Subtract 1 from both sides:
\(\begin{gathered} x+1-1=0-1 \\ \\ x=-1 \end{gathered}\)Now, substitute -1 for x in either of the equations and solve for y.
Let's take the first equation:
\(\begin{gathered} y=x^2-4 \\ \\ y=-1^2-4 \\ \\ y=1-4 \\ \\ y=-3 \end{gathered}\)Therefore, we have the solutions:
x = -1, y = -3
In point form:
(x, y) ==> (-1, -3)
ANSWER:
A. (-1, -3)
- 4x + y = 6
-5.6 - y = 21
Answers
Answer:
1. 10
2. 26.6
Step-by-step explanation:
27x + 45y and 7(9x + 7y) are these equivalent?
Answers
Answer:
No
Step-by-step explanation:
If you want to know whether they are equivalent or no, we will first have to find the value of both.
\(27x+45y\)
Since there aren't any like terms here, your answer would be
\(27x+45y\)
Let's solve for next one.
\(7(9x+7y)\)
Let's add in parenthesis to 7.
\((7)(9x+7y)\)
Now we will separate everything. And also you will have to add.
\((7)(9x)+(7)(7y)\)
Now that we added we got our answer.
\(63x+49y\)
Both values were not the same, so therefore, your answer is no, they are not equivalent.
Hope this helps!
No
Step-by-step explanation:
If you want to know whether they are equivalent or no, we will first have to find the value of both.
Since there aren't any like terms here, your answer would be
Let's solve for next one.
Let's add in parenthesis to 7.
Now we will separate everything. And also you will have to add.
Now that we added we got our answer.
Both values were not the same, so therefore, your answer is no, they are not equivalent.
Hope this helps!
Read more on Brainly.com - https://brainly.com/question/17379473#readmore
Plz help fast only given 5 mins tell if they are similar or not
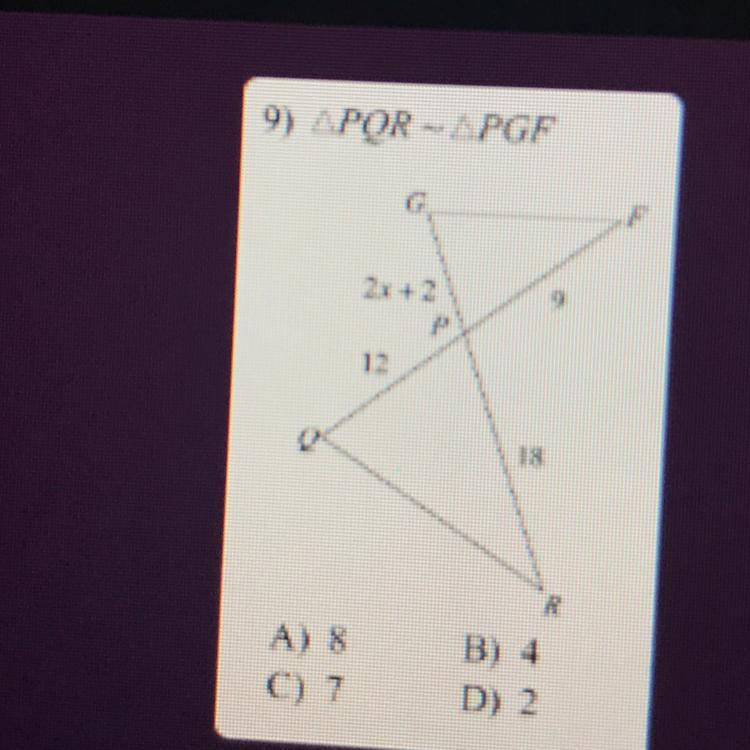
Answers
Answer:
They are not similar.
Step-by-step explanation:
QP would be equal to FP if they were equal but they aren't equal so....yeah
an inverted conical tank full of water has a height of 10 meters and a base radius of 7 meters. how much work is required to pump the water over the upper edge of the tank until the height of the water remaining in the tank is 4 meters? round to the nearest integer. note: the weight-density of water is 9800 nm3.
Answers
the amount of work required to pump the water over the upper edge of the tank until the height of the water remaining in the tank is 4 meters is 8984201 Joules.
To calculate the amount of work required to pump the water over the upper edge of the tank until the height of the water remaining in the tank is 4 meters, use the equation
Work = Force x Distance.
The force required is the weight of the water that needs to be lifted, which is calculated as follows:
Weight of Water = Volume of Water x Weight Density
Here, the Volume of Water = 1/3πr2h
Weight of Water = (1/3πr2) x (h x Weight Density) = (1/3π(7)2) x ((10 - 4) x 9800) = 1497033.52 N
Distance = Height of Water = 10 - 4 = 6 m
Work = Force x Distance = 1497033.52 x 6 = 8984201.12 Joules
Therefore, the amount of work required to pump the water is 8984201.12 Joules, rounded to the nearest integer is 8984201 Joules.
To know more about work refer here:
https://brainly.com/question/30003723
#SPJ11
Juan is organizing his sports cards and boxes he has 2 2/3 boxes of baseball cards 1 5/6 well cards, and two and 18 boxes of basketball cards which collection of cards would fit in for storage boxes about how many boxes does Juan need to store all of his cards?
Answers
Juan needs about 4.39 boxes to store all of his cards. However, since he cannot have a fraction of a box, he would need to round up to the nearest whole box, giving a final answer of 5 boxes.
What is meant by cards?
A "card" usually refers to an element or member of a set or deck of cards, often used in probability and statistics problems. It can also refer to rectangular pieces of paper or material used for sorting or organizing information.
What is meant by a fraction?
A fraction represents a part of a whole or a ratio between two quantities. It is expressed as a number or expression written in the form of "numerator/denominator", where the numerator is the top number and the denominator is the bottom number.
According to the given information
Juan has:
2 2/3 boxes of baseball cards, which can be written as 8/3 boxes
1 5/6 well cards, which can be written as 11/6 boxes
2 and 18 boxes of basketball cards, which can be written as 2.54 boxes (by adding the whole number part 2 to the fractional part 18/12 and simplifying)
To find the total number of boxes needed to store all of Juan's cards, we can add up the number of boxes for each collection:
8/3 + 11/6 + 2.54 = 4.39 (rounded to two decimal places)
To know more about fraction visit
brainly.com/question/10708469
#SPJ1
PLEASE HELPPPPPPPPP:(

Answers
Answer: The first one, y = 3x - 4
Hope this helps :)
Answer:
Option 1, which is y= 3x - 4
The United States five-dollar bill are 155.956 mm long and 66.294 wide. A stack of these bills fits inside a 156 x 66.3 x 66.3 mm box and uses up 258,473.68 cubic millimeters of volume.
Part A: How much money is in the box?
Part B: What percent of the box’s volume is taken up by the five-dollar bills?
Answers
Answer:
A) $5 × 25 = $75
B) 37.69%
Step-by-step explanation:
The dimension of five dollar bill:
Length = 155.956mm
Width = 66.294
Volume of box being occupied by 5 dollar bill = 258,473.68mm^3
Dimension of box :
156 x 66.3 x 66.3 mm
If volume of the 5—dollar bill is 258,473.68mm^3
Then, the Thickness of the five dollar stack equals :
Volume = Length × width × height
258,473.68mm^3 = 155.956mm × 66.294 × height
258,473.68 = 10338.947064 × h
h = (258473.68/10338.947064)
h = 25.000000003288 = 25
Therefore, the amount of money in the box is:
$5 × 25 = $75
Percentage of box volume taken up by $5 bill
Volume of the box:
156 x 66.3 x 66.3 mm = 685727.6399mm^3
Volume of box being occupied by 5 dollar bill = 258,473.68mm^3
(258,473.68 / 685727.6399) × 100
=37.69%
At the end of 1st Quarter of 2009 the median price of a single-family home in Charleston/No. Charleston was $184,990. Single-family home prices in Charleston/No. Charleston decreased from the 1st Qtr of 2008 by 8.15%. NOTE: Depreciation means a negative value for r. (a). Estimate the median price of a single-family home in the 1st Qtr of 2008.
(b). If the median price of a single-family home falls at the same rate for the next 2 years, estimate the median price of a single-family home in the 1st Qtr of 2011.
Answers
The estimated median price of a single-family home in Charleston/No. Charleston in the 1st Quarter of 2008 is $201,048. If the median price continues to decrease at the same rate for the next two years, the estimated median price of a single-family home in the 1st Quarter of 2011 would be $144,458.
(a) To estimate the median price of a single-family home in the 1st Quarter of 2008, we need to calculate the original price before the 8.15% decrease. Let's assume the original price was P. The price after the decrease can be calculated as P - 8.15% of P, which translates to P - (0.0815 * P) = P(1 - 0.0815). Given that the end of 1st Quarter of 2009 median price was $184,990, we can set up the equation as $184,990 = P(1 - 0.0815) and solve for P. This gives us P ≈ $201,048 as the estimated median price of a single-family home in the 1st Quarter of 2008.
(b) If the median price of a single-family home falls at the same rate for the next two years, we can calculate the price for the 1st Quarter of 2011 using the estimated median price from the 1st Quarter of 2009. Starting with the median price of $184,990, we need to apply an 8.15% decrease for two consecutive years. After the first year, the price would be $184,990 - (0.0815 * $184,990) = $169,805.95. Applying the same percentage decrease for the second year, the price would be $169,805.95 - (0.0815 * $169,805.95) = $156,012.32. Therefore, the estimated median price of a single-family home in the 1st Quarter of 2011 would be approximately $144,458.
To learn more about median click here: brainly.com/question/300591
#SPJ11
f(x)=4 divided by x-2, x is supposed to be in absolute value
Answers
Absolute value of x-2 is +(x-2) 4,2, 4/3
What is Absolute value?
Absolute value is an important math concept to understand. To represent the absolute value of a number, we use a vertical bar on either side of the number.
The function f(x) = 4/|x-2| has a vertical asymptote at x=2, meaning the function approaches infinity as x approaches 2 from both the left and the right. The function is also symmetric about the vertical line x=2.
To sketch the graph of this function, we can start by plotting some points. For x<2, the absolute value of x-2 is -(x-2), so we have:
f(1) = 4/|-1| = 4
f(0) = 4/|-2| = 2
f(-1) = 4/|-3| = 4/3
For x>2, the absolute value of x-2 is +(x-2), so we have:
f(3) = 4/|1| = 4
f(4) = 4/|2| = 2
f(5) = 4/|3| = 4/3
To know more about Absolute value visit,
https://brainly.com/question/12928519
#SPJ1
Consider the following acceleration d^2s/dt^2, initial velocity, and initial position of an object moving on a number line. Find the object's position
at time t.
a = 9.8, v(0) = - 15, s(0) =
Answers
s(t) = -15t + 4.9t^2 This equation represents the object's position at time t on the number line.
To find the object's position at time t, we need to use the equation for displacement:
s(t) = s(0) + v(0)t + 1/2at^2
Plugging in the given values, we get:
s(t) = s(0) + v(0)t + 1/2at^2
s(t) = -15(0) + 1/2(9.8)(t^2)
s(t) = 4.9t^2
Therefore, the object's position at time t is given by the equation s(t) = 4.9t^2.
To find the object's position at time t, we can use the following formula:
s(t) = s(0) + v(0)t + 0.5at^2
Given the values a = 9.8, v(0) = -15, and s(0) = 0, we can substitute them into the formula:
s(t) = 0 + (-15)t + 0.5(9.8)t^2
s(t) = -15t + 4.9t^2
To learn more about equation click here
brainly.com/question/29657983
#SPJ11
