-7w^2 + 2w if w = -4 Evaluate each expression given the variable replacement

A pipe whose diameter measures 1 1/4 inches should have less threads per inch than a pipe with a diameter of 11/2 inch. So, the correct answer is (D).

To determine the correct answer, we need to compare the diameters of the two pipes and understand the relationship between pipe diameter and threads per inch.

The number of threads per inch generally decreases as the pipe diameter increases. This means that a larger pipe diameter will have fewer threads per inch compared to a smaller pipe diameter.

Given that the first pipe has a diameter of 1 1/4 inches, we need to find the pipe diameter from the options that is larger than 1 1/4 inches.

The option that meets this requirement is D. 11/2. This represents a pipe diameter of 1 1/2 inches. Therefore, a pipe with a diameter of 1 1/2 inches should have fewer threads per inch than a pipe with a diameter of 1 1/4 inches. Therefore, the correct answer is D. 11/2.

For more questions on: diameter

https://brainly.com/question/30460318

#SPJ8  

The rate (in km/h) at which the distance from the plane to the radar station is increasing a minute later is 0 km/h (rounded to the nearest whole number).

To solve this problem, we can use the concepts of trigonometry and related rates.

Let's denote the distance from the plane to the radar station as D(t), where t represents time. We want to find the rate at which D is changing with respect to time (dD/dt) one minute later.

Given:

The plane is flying with a constant speed of 360 km/h.

The plane passes over the radar station at an altitude of 1 km.

The plane is climbing at an angle of 30°.

We can visualize the situation as a right triangle, with the ground radar station at one vertex, the plane at another vertex, and the distance between them (D) as the hypotenuse. The altitude of the plane forms a vertical side, and the horizontal distance between the plane and the radar station forms the other side.

We can use the trigonometric relationship of sine to relate the altitude, angle, and hypotenuse:

sin(30°) = 1/D.

To find dD/dt, we can differentiate both sides of this equation with respect to time:

cos(30°) * d(30°)/dt = -1/D^2 * dD/dt.

Since the plane is flying with a constant speed, the rate of change of the angle (d(30°)/dt) is zero. Thus, the equation simplifies to:

cos(30°) * 0 = -1/D^2 * dD/dt.

We can substitute the known values:

cos(30°) = √3/2,

D = 1 km.

Therefore, we have:

√3/2 * 0 = -1/(1^2) * dD/dt.

Simplifying further:

0 = -1 * dD/dt.

This implies that the rate at which the distance from the plane to the radar station is changing is zero. In other words, the distance remains constant.

for such more question on distance

https://brainly.com/question/7243416

#SPJ8

We have shown that C is the image of A by dilation with center B and ratio 3.

Now, To show that C is the image of A by dilation with center B and ratio 3, we need to follow these steps:

Firstly, Find the vector AB by subtracting the coordinates of B from the coordinates of A:

AB = A - B = (6 - 3, 4 - 7) = (3, -3)

Multiply the vector AB by the dilation ratio of 3:

3 AB = 3 (3, -3)  = (9, -9)

Add the resulting vector to the coordinates of the center B:

BC = B + 3 AB = (3, 7) + (9, -9)

BC = (12, -2)

Hence, Compare the resulting point BC to the coordinates of C to show that they are the same:

BC = (12, -2) = C

Therefore, we have shown that C is the image of A by dilation with center B and ratio 3.

Learn more about the coordinate visit:

https://brainly.com/question/24394007

#SPJ1

Answer:

42.39 ft²

Step-by-step explanation:

area of sector= 3/8 × 3.14 × 6²

= 42.39 ft²

The area of the sector is 42.39 ft²

Given that, a sector of a circle has a diameter of 12 feet and an angle of 3pi/4 radians, we need to find the area of the sector,

Area of the sector = θ/360° / π·radius²

area of sector= 3/8 × 3.14 × 6²

= 42.39 ft²

Hence, the  area of the sector is 42.39 ft²

Learn more about the sector of the circle, click;

https://brainly.com/question/15591260

#SPJ2

Answer:

w√6w

I think this is what u were needed if it was please please please mark me the brainliest if not please let me know so I can figure out what I'm missing :)

Answer:

4a + 3d + 15

Step-by-step explanation:

Remove parentheses.

3d + 9 + 4a + 6  

Add 9 and 6.

3d + 4a + 15  

Reorder 3d and 4a.  

4a + 3d + 15

Answer:

y = - 5

Step-by-step explanation:

y = 4 is a horizontal line parallel to the x- axis

A parallel line must therefore be a horizontal line with equation

y = c

where c is the value of the y- coordinates the line passes through.

The line passes through (1, - 5) with y- coordinate - 5, thus

y = - 5 ← equation of parallel line

By substitution; x = 4 and y = -31

An equation is a mathematical statement that shows that two mathematical expressions are equal. It shows the relationship of equality between the expression written on the left side with the expression written on the right side. Equations can be solved to find the value of an unknown variable representing an unknown quantity.

y=-6x-7 --- 1

7x+y=-3 --- 2

Substituting y as 6x - 7 in equation 2

7x + (-6x - 7) = -3

7x - 6x - 7 = -3

x - 7 = -3

x = -3 + 7

x = 4

Substitute x as 4 in equation 1

y = -6x - 7

y = -6(4) - 7

y = -24 - 7

y = -31

Learn more about equations here: https://brainly.com/question/22688504

#SPJ1

Answer: 283.3333333% (283.3%)

Step-by-step explanation:

First, lets turn 2 5/6 into and improper fraction. It becomes 17/6.

Now, we divide 17/6

17/6 = 2.833333333

Now, to turn it into a percent, we multiply it by 100, or move the decimal point 2 places to the right. That gives us 283.3333333% (283.3%)

Hope this helps!

Complete question is;

An advertising banner has four sections, as modeled in the attached image. Two sections are congruent trapezoids, and two sections are congruent right triangles. Which measurement is the best estimate of the area of the banner in square meters?

Answer:

6 m²

Step-by-step explanation:

Since we are told that there are two congruent trapezoid, it means that they will have same base of 1m.

This Means the total base of the entire triangle will be;

Base = 1 + 1¾ + 1 + 1¾ = 5.5 m

Height of main triangle = 2 m

Thus,

Area = ½ × 5.5 × 2 = 5.5 m²

We are looking for best estimate, so let's approximate to the nearest whole number to get 6 m²

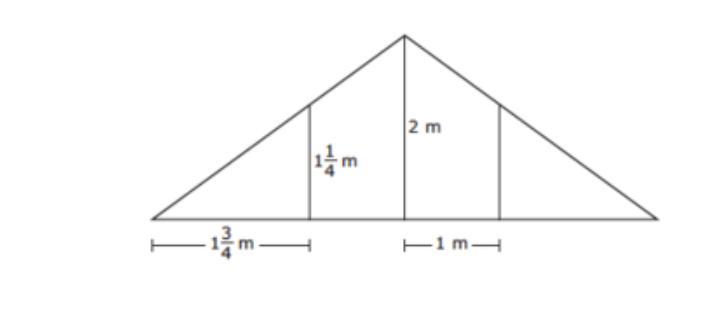
Answer:

6 m²

Step-by-step explanation:

Since we are told that there are two congruent trapezoid, it means that they will have same base of 1m.

his Means the total base of the entire triangle will be;

Base = 1 + 1¾ + 1 + 1¾ = 5.5 m

Height of main triangle = 2 m

Now you have

Area = ½ × 5.5 × 2 = 5.5 m²

We are looking for best estimate, so if you round 5.5 now remember 5 or more raise the score 4 or less let it rest leaving you with 6 m².

Answer:

Systematic Random Sampling

Step-by-step explanation:

Edge 2021

Answer:

Systematic Random Sampling

Step-by-step explanation:

Took the test.

Answer:

.31

Step-by-step explanation:

Answer:

0.31

Step-by-step explanation:

Answer:

a) 0.3174 = 31.74% probability of a defect. The number of defects for a 1,000-unit production run is 317.

b) 0.0026 = 0.26% probability of a defect. The expected number of defects for a 1,000-unit production run is 26.

c) Less variation means that the values are closer to the mean, and farther from the limits, which means that more pieces will be within specifications.

Step-by-step explanation:

Normal Probability Distribution:

Problems of normal distributions can be solved using the z-score formula.

In a set with mean \(\mu\) and standard deviation \(\sigma\), the zscore of a measure X is given by:

\(Z = \frac{X - \mu}{\sigma}\)

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.

Assume a production process produces items with a mean weight of 10 ounces.

This means that \(\mu = 10\).

Question a:

Process standard deviation of 0.15 means that \(\sigma = 0.15\)

Calculate the probability of a defect.

Less than 9.85 or more than 10.15. Since they are the same distance from the mean, these probabilities is the same, which means that we find 1 and multiply the result by 2.

Probability of less than 9.85.

pvalue of Z when X = 9.85. So

\(Z = \frac{X - \mu}{\sigma}\)

\(Z = \frac{9.85 - 10}{0.15}\)

\(Z = -1\)

\(Z = -1\) has a pvalue of 0.1587

2*0.1587 = 0.3174

0.3174 = 31.74% probability of a defect.

Calculate the expected number of defects for a 1,000-unit production run.

Multiplication of 1000 by the probability of a defect.

1000*0.3174 = 317.4

Rounding to the nearest integer,

The number of defects for a 1,000-unit production run is 317.

Question b:

Now we have that \(\sigma = 0.05\)

Probability of a defect:

Same logic as question a.

\(Z = \frac{X - \mu}{\sigma}\)

\(Z = \frac{9.85 - 10}{0.05}\)

\(Z = -3\)

\(Z = -3\) has a pvalue of 0.0013

2*0.0013 = 0.0026

0.0026 = 0.26% probability of a defect.

Expected number of defects:

1000*0.0026 = 26

The expected number of defects for a 1,000-unit production run is 26.

(c) What is the advantage of reducing process variation, thereby causing process control limits to be at a greater number of standard deviations from the mean?

Less variation means that the values are closer to the mean, and farther from the limits, which means that more pieces will be within specifications.

Answer:

0.0713 = 7.13% probability that the result is positive.

Step-by-step explanation:

Probability of a positive test:

91% of 1/650(has the disease).

7% of 1 - 1/650 = 649/650(does not have the disease). So

\(p = 0.91\frac{1}{650} + 0.07\frac{649}{650} = \frac{0.91 + 0.07*649}{650} = 0.0713\)

0.0713 = 7.13% probability that the result is positive.

Answer:

21

Step-by-step explanation:

Volume of a cuboid is given by

V = l*w*h

924 = 4 (x+1) (x+11)

FOIL

924 = 4(x^2 +11x+x+11)

924 = 4(x^2+12x+11)

Divide each side by 4

231 = (x^2+12x+11)

Subtract 231 from each side

0 = x^2 +12x +11-231

0 = x^2 +12x - 220

Factor

0 = (x+22) (x-10)

Using the zero product property

x+22 =0  x-10 =0

x=-22  x=10

We cannot have a negative length

x=10

The side lengths are 4, 10+1, 10+11

4,11,21

The longest is 21

Answer:759

Step-by-step explanation:

Answer:

The equation of a parabola that has a curvature 6 at the origin is \(f(x) = 3\cdot x^{2}\).

Step-by-step explanation:

All parabolas are represented by second-order polynomials, whose standard form is:

\(f(x) = a\cdot x^{2}+b\cdot x + c\) (Eq. 1)

Where:

\(x\) - Independent variable, dimensionless.

\(y\) - Dependent variable, dimensionless.

\(a\), \(b\), \(c\) - Coefficient of the parabola, dimensionless.

From Vectorial Calculus we know that curvature (\(K\)), dimensionless, is defined by the following expression:

\(K = \frac{\left|\frac{d^{2}y}{dx^{2}} \right|}{\left[1+\left(\frac{dy}{dx} \right)^{2}\right]^{\frac{3}{2} }}\) (Eq. 2)

Where \(\frac{dy}{dx}\) and \(\frac{d^{2}y}{dx^{2}}\) are the first and second derivatives of the function, respectively. Each expression is described below:

\(\frac{dy}{dx} = 2\cdot a\cdot x + b\)

\(\frac{d^{2}y}{dx^{2}} = 2\cdot a\)

If we know that \(a > 0\), \(b = c = 0\), \(x = 0\) and \(K = 6\), then the equation of curvature and polynomial are, respectively:

\(\frac{2\cdot a}{1^{\frac{3}{2} }} = 6\)

\(a = 3\)

The equation of a parabola that has a curvature 6 at the origin is \(f(x) = 3\cdot x^{2}\).

An equation of a parabola that has curvature 6 at the origin is \(\rm f(x) = 3x^2\).

We have to determine

An equation of a parabola that has curvature 6 at the origin.

The equation of a parabola that has a curvature a at the origin is;

\(\rm f(x) = ax^2\)

The value of a is given by k(0) = 8;

\(\rm k(0) = 2a\\\\6 = 2a\\\\a = \dfrac{6}{2}\\\\a=3\)

Therefore,

The equation of a parabola that has a curvature a at the origin is;

\(\rm f(x) = ax^2\)

\(\rm f(x) = 3x^2\)

Hence, an equation of a parabola that has curvature 6 at the origin is \(\rm f(x) = 3x^2\).

To know more about Parabola click the link given below.

https://brainly.com/question/5913342

Answer:the answer is 319.857 and round to 320

Step-by-step explanation:

Answer: Acute angle

Step-by-step explanation:

because it is at a 62 I think angle

Answer:

Step-by-step explanation:

A) To find the maximum weekly profit, we need to find the vertex of the quadratic function m(x)=-300x^2+978x-570. The x-coordinate of the vertex is -b/2a, where a=-300 and b=978. Therefore, x=-978/(-600) = 1.63. To find the corresponding y-coordinate, we substitute x=1.63 into the function m(x) and get m(1.63)=-300(1.63)^2+978(1.63)-570 = 346.62. So the maximum weekly profit is $346.62, and the price of a cup of coffee that produces that maximum profit is $1.63.

B) The function h(x) = m(x - 2.5) shifts the graph of m(x) 2.5 units to the right. This means that the vertex of h(x) is located at x = 1.63 + 2.5 = 4.13. The value of the vertex of h(x) is the same as the value of the vertex of m(x) since shifting the graph horizontally does not affect the maximum value of the function. Therefore, h(x) has the same maximum value as m(x).

C) To find the price per cup of coffee that Delish Coffee must charge to produce a maximum profit, we need to find the x-value that maximizes the function h(x) = m(x - 2.5). From part A, we know that the maximum value of m(x) occurs at x = 1.63. So the maximum value of h(x) occurs at x = 1.63 + 2.5 = 4.13. Therefore, Delish Coffee must charge $4.13 per cup of coffee to produce a maximum profit.

D) The function k(x) = m(x) - 115 is the profit function for a coffee house that charges $115 less per cup of coffee than the coffee house in part A. The maximum value of k(x) will occur at the same x-value as m(x), since the value of x that maximizes the profit is independent of the constant term (-115 in this case). However, the maximum value of k(x) will be 115 dollars less than the maximum value of m(x), since k(x) is the profit function for a coffee house that charges $115 less per cup of coffee.

When matched, the prompts on asymptotes would be:

The presence of a vertical asymptote at x=0 signifies that the cost of producing pills can never reach a value of 0, remaining persistently positive. Simultaneously, the horizontal asymptote at y=0 serves as a reassuring indication that the cost of producing pills cannot be negative, as it steadfastly remains at or above zero.

This crucial constraint ensures that the cost incurred in the pill production process is always a non-negative quantity. Consequently, the prompt related to the impossibility of negative costs aligns with this notion.

Find out more on horizontal asymptote at https://brainly.com/question/1851758

#SPJ9

They can buy 120 vans, 60 small trucks, and 80 large trucks.

The truck company plans to spend 10 million on 260 vehicles. Each commercial van cost 25,000 dollars. Each small truck 50,000 dollars and each large truck 50,000 dollars. They needed twice as many van as small truck

Therefore,

let

s = number of small truck

number of van = v

let

l = number of large truck

v + s + l = 260

25,000(v) + 50,000(s) + 50,000(l) = 10,000, 000

v + 2s + 2l = 400

Hence,

v = 2s

So,

2s + 2s + 2l = 400

4s + 2l = 400

2s + s + l = 260

3s + l = 260

2s + l = 200

s = 60

l = 200 - 2(60)

l = 200 - 120

l = 80

v = 2(600 = 120

Therefore, they can buy the following:

number of small truck = 60

number of van = 120

number of large truck = 80

learn more on cost here: brainly.com/question/27903912

#SPJ1

Answer:

14 weeks

Step-by-step explanation:

Simply divide 200 by 15, then round up because the answer should be a full week:

200 / 15 = 13.3333 ≈ 14 weeks

For an equation, let x be weeks passed and y be money left. Since the money is spent at a constant rate, the equation will have a constant slope, and the y intercept is 200, since at no money spent, Micah has $200:

y = -15x + 200

For a ratio table, it might look something like this:

weeks  :  money

0       :      $200

1        :      $185

2       :      $160

3       :      $145

Answer:

v= -15x + 200 x 213.33 weeks 6= 15x + 200 the answer is 13

Hey, do u want to g mail?

Answer:

There were 186 math textbooks sold and 62 physics textbooks sold.

Given:

- 248 books sold in total

- math textbooks and physics textbooks sold

- math is three times physics

Step-by-step explanation:

[] First, we can set up mathematical equations for this scenario;

       - Let m be math textbooks and p be physics textbooks

m = 3p

248 = p + (3p)

248 = 4p

62 = p

[] Now we can solve for the amount of each books sold;

p = 62 books

3 * p = m

3 * 62 = m

m = 186

[] Lastly, we can check to make sure this will work;

186 + 62 = 248 ✓

Have a nice day!

     I hope this is what you are looking for, but if not - comment! I will edit and update my answer accordingly.

- Heather

There can be multiple outputs (monthly charges) for a given input (number of credit cards), violating the definition of a function. hence, Situation 3 does not represent a function.

Situation 3: the total amount of money charged monthly on credit cards to the number of credit cards owned does not represent a function.

In a function, each input (or x-value) should have a unique output (or y-value). However, in this situation, the total amount of money charged monthly on credit cards depends on the number of credit cards owned. It is possible to have different credit card numbers but still have the same total amount of money charged monthly.

For example, two people could own different numbers of credit cards but have the same monthly charges.

As a result, the definition of a function can be violated by having many outputs (monthly charges) for a single input (number of credit cards).

Because of this, case 3 does not represent a function.

for such more question on function

https://brainly.com/question/16332322

#SPJ8

66) The number of feet of fencing that Ms. Hamilton needs to buy is 75 feet.

67) The distance around a rectangle is called a perimeter.

The use of Mathematics skills is all-encompassing. Every activity involves some mathematical calculations and the use of mathematical operations, like additions, subtractions, divisions, and multiplication.

When you visit a Merchandise Store, you undertake some mathematical activities by computing how much is needed and the balance you will get. Future projections depend on maths skills.

For instance, budgeting how much it costs you weekly to maintain your hairstyle also involves maths skills.

As you return to school after the summer breaks, you decide how much savings you must spend. It is maths.  Any time calculations are involved, it requires maths.

Length of the yard = 24.75 feet

Width of the yard = 12.75 feet

Perimeter of the yard = 75 feet (24.75 + 12.75)2

Charges for a yard of iron fencing = $50 per yard

3 feet = 1 yard

75 feet = 25 yards (75/3)

The cost of 25 yards = $1,250

Thus, Ms. Hamilton will need to spend $1,250 on this decorative iron fence project.

Learn more about mathematical skills at https://brainly.com/question/23945932

#SPJ1

The area of triangle EFG is given as follows:

A = 18.63 square units.

The area of a rectangle of base b and height h is given by half the multiplication of dimensions, according to the formula presented as follows:

A = 0.5bh

The base is given by segment EF as follows:

\(EF = \sqrt{(9 - 4)^2 + (-7 -(-9))^2}\)

EF = 5.4.

The midpoint of EF is given as follows:

M(6.5, -8).

The height is given by the segment MG as follows:

\(MG = \sqrt{(6.5 - 3)^2 + (-2 - (-8))^2}\)

MG = 6.9.

Hence the area is given as follows:

A = 0.5bh

A = 0.5 x 5.4 x 6.9

A = 18.63 square units.

More can be learned about the area of a triangle at brainly.com/question/21735282

#SPJ1

Answer:

C. -3/7

Step-by-step explanation:

parallel lines have the same slope.

If the slope of a line is - 3/7, then the line parallel to it also has a slope of -3/7

Therefore the answer is C

Answer:

\(\angle L = 73^o\)

Step-by-step explanation:

Given

\(\angle M = 107^o\)

Required

Find \(\angle L\)

From the question, we understand that: \(\angle M\) and \(\angle L\) form a linear pair;

This implies that:

\(\angle M + \angle L = 180^o\)

So, we have:

\(107^o + \angle L = 180^o\)

Collect like terms

\(\angle L = 180^o -107^o\)

\(\angle L = 73^o\)