A company sells widgets. The amount of profit, y, made by the company, is related to the selling price of each widget, x, by the given equation. Using this equation, find out the maximum amount of profit the company can make, to the nearest dollar. �
=
−
8
�
2
+
242
�
−
1056
y=−8x
2
+242x−1056
Answers
The maximum amount of profit the company can make is approximately $1832by using the given equation y = -8x² + 242x – 1056.
To find the maximum profit the company can make, we need to find the vertex of the quadratic equation y = -8x² + 242x - 1056.
The x-coordinate of the vertex is given by x = -b/2a, where a = -8 and b = 242. Substituting these values gives x = -242/(2*(-8)) = 15.125.
To find the corresponding y-coordinate, we substitute x = 15.125 into the equation y = -8x² + 242x - 1056, which gives y = 1832.
Therefore, the maximum amount of profit the company can make is $1832.
Learn more about the quadratic equations here: brainly.com/question/30098550
#SPJ4
Related Questions
How do you find ratios?
Answers
For example, if there are 5 blue balls and 7 red balls. the ration of the blue balls with the red balls is
\(5\colon7\)it can also be written as a fraction :
\(\frac{5}{7}\)It is important to put the one that was mentioned first in the numerator. in this case is blue ball, that's why 5 came first. If we are asked what is the ratio of the red balls with the blue balls , then we will have to indicate 7 first. The ratio will have to be
\(\begin{gathered} 7\colon5 \\ or \\ \frac{7}{5} \end{gathered}\)The sequence is important.
POSSIBLE POINTS: 10
length of a rectangle is 6 feet longer than the width. If the width of the rectangle is w feet long, which of the following expressions represents the
meter of the rectangle?

Answers
Answer:
4w + 12
Step-by-step explanation:
Perimeter of a rectangle = 2(length + width)
Let
Width of the rectangle = w feet
Length of the rectangle = (w + 6) feet
Perimeter of a rectangle = 2(length + width)
= 2{(w+6) + w}
= 2(w + 6 + w)
= 2(2w + 6)
= 4w + 12
Perimeter of a rectangle = (4w + 12) feet
the greatest common factor of the binomial 2 x − 4 is 2 . the greatest common factor of the binomial 4 x 8 is 4 . what is the greatest common factor of their product, ( 2 x − 4 ) ( 4 x 8 ) , when it has been multiplied out?
Answers
The greatest common factor of their product is 2
How to determine the greatest common factor of the productFrom the question, we have the following parameters that can be used in our computation:
GCF of 2x - 4 = 2
GCF of 4 * 8 = 4
Using the above as a guide, we have the following expressions
GCF of 2x - 4 = 2
GCF of 4 * 8 = 2 * 2
Write out the common factors
GCF = 2
This means that the GCF is 2
Read more about GCF at
https://brainly.com/question/17067741
#SPJ1
Please help!!
Answers:
A)Triangle HGF is congruent to triangle FEH.
B) Triangle GFH is congruent to EFH
C) Angle KHE is congruent to angle KHG
D)Angle GHK is congruent to angle EFK
E)Segment EH is congruent to segment GH
F)Segment HG is congruent to FE
G)Segment FH is congruent to segment HF
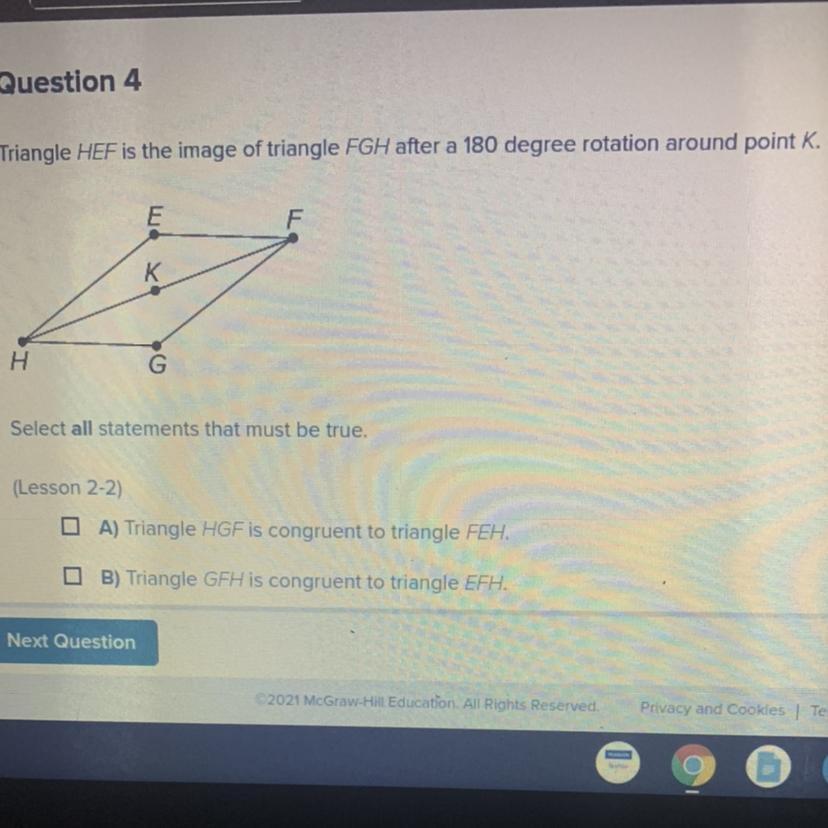
Answers
Answer:
I guess HEF is congruent to GFH
But it's just guess I'm not confirm
Answer:
A.
Step-by-step explanation:
the triangle HGF is congruent to traingle FEH
If u understand this May u help me please

Answers
Answer:
y=1/6x+2
Step-by-step explanation:
To start, you know what m is; it's just the slope, which you said was 1/6. So you can right away fill in the equation for a line somewhat to read:
y=1/6x+b.
Now, what about b, the y-intercept?
To find b, think about what your (x,y) point means:
(12,4). When x of the line is 12, y of the line must be 4.
Because you said the line passes through this point, right?
Now, look at our line's equation so far: . b is what we want, the 1/6 is already set and x and y are just two "free variables" sitting there. We can plug anything we want in for x and y here, but we want the equation for the line that specfically passes through the the point (12,4).
So, why not plug in for x the number 12 and for y the number 4? This will allow us to solve for b for the particular line that passes through the point you gave!.
(12,4). y=mx+b or 4=1/6 × 12+b, or solving for b: b=4-(1/6)(12). b=2.
Please help‼️ domain and range‼️

Answers
The domain and the range of the function are (-∝, ∝) and (0, ∝), respectively
Calculating the domain and range of the graph?From the question, we have the following parameters that can be used in our computation:
The graph
The above graph is an exponential function
The rule of an function is that
The domain is the set of all real values
In this case, the domain is (-∝, ∝)
For the range, we have
Range = (0, ∝)
Read more about domain and range at
brainly.com/question/27910766
#SPJ1
Can someone please help me with the graph above ?? please

Answers
Answer:
See image
Step-by-step explanation:
The third line of the directions that says
(x,y)->(x-5, y)
is telling you to look at each point and keep the y the same, but subtract 5 from the x. For example, point B which is given as the point (4,-1) will slide over 5 places to the left and keep the y the same to (-1,-1) see image
The whole shape will slide over to the left 5 places. (red)
Then, it says reflect over y=0. Which is a flip like a mirror image.(green) The final answer is the green figure.

Assume that the heights of men are normally distributed with a mean of 69.8 inches and a standard deviation of 2.4 inches. If 36 men are randomly selected, find the probability that they have a mean height greater than 70.8 inches.
Answers
The probability that 36 randomly selected men have a mean height greater than 70.8 inches is 0.0062 or 0.62%.
To solve this problem, we can use the central limit theorem and the formula for the z-score.
First, we need to calculate the standard error of the mean, which is the standard deviation divided by the square root of the sample size:
standard error of the mean = 2.4 / √(36) = 0.4
Next, we can calculate the z-score for a sample mean of 70.8 inches:
z = (70.8 - 69.8) / 0.4 = 2.5
We can use a standard normal distribution table or calculator to find the probability that the z-score is greater than 2.5. This probability is approximately 0.0062 or 0.62%.
Therefore, the probability that 36 randomly selected men have a mean height greater than 70.8 inches is 0.0062 or 0.62%.
To learn more about probability here:
brainly.com/question/30034780#
#SPJ11
Simplify each rational expression. State any restrictions on the variable. x² -2 x-24 / x² +7 x+12 . x² -1 / x-6
Answers
A rational expression is an algebraic expression that represents a ratio of two polynomials, where the denominator is not equal to zero.
To simplify the rational expression (\(x^2\) - 2x - 24) / (\(x^2\) + 7x + 12) * (\(x^2\) - 1) / (x - 6), we can follow these steps:
Step 1: Factorize the numerators and denominators.
The numerator (\(x^2\) - 2x - 24) can be factored as (x - 6)(x + 4), and the denominator (\(x^2\) + 7x + 12) can be factored as (x + 4)(x + 3).
The numerator (\(x^2\) - 1) can be factored as (x - 1)(x + 1), and the denominator (x - 6) cannot be factored any further.
Step 2: Cancel out any common factors between the numerators and denominators.
We can cancel out the (x - 6) and (x + 4) terms from both the numerator and the denominator.
Step 3: Simplify the expression.
After canceling out the common factors, we are left with the simplified expression:
(x + 4)(x - 1)(x + 1) / (x + 3)(x - 6)
Step 4: State any restrictions on the variable.
To find any restrictions on the variable, we need to look at the original expression. In this case, we have a denominator of (x - 6), so the variable x cannot be equal to 6.
Therefore, the simplified rational expression is:
(x + 4)(x - 1)(x + 1) / (x + 3)(x - 6), with a restriction on the variable x: x ≠ 6.
To know more about rational expression visit:
https://brainly.com/question/30488168
#SPJ11
determine the positions of the keys in a hash table of size n = 7 and insert them into the hash table. resolve collisions by linear probing. do not resize. keys: 34, 78, 93, 5, 74, 81
Answers
The positions of the keys in a hash table of size n = 7 has been determined and the collisions are resolved by linear probing.
To determine the positions of the keys in a hash table of size n=7 and insert them into the hash table while resolving collisions by linear probing, we need to first apply a hash function that maps the keys to a specific position in the table. Let's assume that we use the simple mod function as the hash function: h(key) = key % 7.
Using this hash function, the keys will be mapped to the following positions in the hash table:
- 34 -> h(34) = 6
- 78 -> h(78) = 1
- 93 -> h(93) = 2
- 5 -> h(5) = 5
- 74 -> h(74) = 4
- 81 -> h(81) = 4
We can see that two keys, 74 and 81, are mapped to the same position in the table (position 4). This is called a collision. To resolve collisions using linear probing, we simply look for the next available position in the table and insert the key there.
Starting from the position of the collision (position 4), we check the next positions in the table sequentially until we find an empty position. The keys will be inserted into the following positions:
- 34 -> position 6
- 78 -> position 1
- 93 -> position 2
- 5 -> position 5
- 74 -> position 4 (original position)
- 81 -> position 5 (next available position after collision)
Therefore, the final hash table with the keys inserted using linear probing will look like this:
0 | |
1 |78|
2 |93|
3 | |
4 |74|
5 |5|
6 |34|
Learn more about linear probing here:
https://brainly.com/question/31518767
#SPJ11
Taylor has a points card for a movie theater.
She receives 75 rewards points just for signing up.
She earns 6.5 points for each visit to the movie theater.
She needs at least 100 points for a free movie ticket.
Which inequality can be used to determine v, the minimum number of visits Taylor needs to earn her first free movie ticket?
Answers
The inequality used to determine v, the minimum number of visits Taylor needs to earn her first free movie ticket is 75 + 6.5v ≥ 100.
What are Linear Inequalities?Linear inequalities are defined as those expressions which are connected by inequality signs like >, <, ≤, ≥ and ≠ and the value of the exponent of the variable is 1.
Given,
Points for signing up = 75 points
Points for each visit to the movie theater = 6.5 points
Let v be the minimum number of visits Taylor needs to earn her first free movie ticket.
Points earned for v visits = 6.5v
She needs at least 100 points for a free movie ticket.
75 + 6.5v will be the points she earn for a free movie ticket.
This expression must be greater than 100, which is the required points for a free movie.
75 + 6.5v ≥ 100
Hence the inequality representing the situation is 75 + 6.5v ≥ 100.
Learn more about Inequalities here :
https://brainly.com/question/19516092
#SPJ1
Drag each tile to the correct location on the image. Each tile can be used more than once, but not all images will be used.
Consider function f.
f(z) = √8x + 4
Y
I
8
To determine the inverse of function f,
change f(x) to y, switch and y,
and solve for
The resulting function can be written as
f-¹(x) = (x - )³.

Answers
The inverse function of f(x) is f⁻¹(x) = (1/8) [(x-4)³]
And the order of tiles is x, y, (1/8), and 4.
The inverse of function:An inverse function is defined as a function, which is converted into another function. In simple words, if any function takes x to y then, the inverse of the function will take y to x, and If the function is denoted by ‘f(x)’, then the inverse function is denoted by f⁻¹(x)
Finding Inverse function:Step 1 => Replace f(x) with y
Step 2 => Switch x and y
Step 3 => Solve for the value of y in terms of x
Step 4 => Replace y with f⁻¹(x) then the resultant function will be the
the inverse of the function
Here we have
f(x) = ∛8x + 4
Step 1 => Replacing f(x) with y
To determine the inverse of the function change f(x) to y
=> y = ∛8x + 4
Step 2 => Switch x and y
=> x = ∛8y + 4
Step 3 => Solve for the value of y in terms of x
=> ∛8y = x - 4
=> y = (x - 4) /∛8
Cubing on both sides
=> y = [ (x - 4) /∛8 ]³
=> y = [ (x -4)³/8 ]
=> y = (1/8) [(x-4)³]
Step 4 => Replace y with f⁻¹(x)
=> f⁻¹(x) = (1/8) [(x-4)³]
Therefore,
The inverse function of f(x) is f⁻¹(x) = (1/8) [(x-4)³]
And the order of tiles is x, y, (1/8) and 4
Learn more about Functions at
https://brainly.com/question/28595513
#SPJ1
Bentley took a ride on Rudolph’s back. At 8:00 pm, he counted 68 stars. At 10:00 pm, he counted twice as many stars. At 12:00 am, he counted five times more stars than his first count.
A. How many stars did Bentley count at 10:00 pm?
B. How many stars did Bentley count at 12:00 am?
Answers
Answer:
A. 136 stars
B. 340 stars
Answer:
At 10 pm he counted 136 stars and at 12 pm he counted 340
Step-by-step explanation:
for 10 pm:
68 x 2
for 12 pm:
68 x 5
Find the distance between (1, -5) and (-6, 2).
**If necessary, round to the nearest tenth**
98 units
34 units
9.9 units
5.8 units
Answers
Answer:
d = 9.9 units
Step-by-step explanation:
Picture a right triangle with one acute vertex at (1, -5) and the other at (-6, 2). Going from one to the other, we see a change in x (run) of 7 and a change in y of 7. Applying the Pythagorean Theorem, we find the distance between the two points as follows:
d = √(7² + 7²) = 7√2, or approximately 9.9 units.
Which is the graph of the linear inequality 1/2x-2y>-6y
Answers
Answer: Are you high school because GOD that looks hard to do.
Step-by-step explanation:
A train to new york city leaves every 7 minutes. another train to boston leaves the station every 6 minutes. suppose it is 6:30 am right now. at what time will both trains leave the station together again if both of them left the station together at 6:30 am?
Answers
Both trains will leave the station together again at 7:12 am if both of them left the station together at 6:30 am.
What is LCM?The lowest integer that is a multiple of two or more numbers is known as the LCM. For instance, the LCM of 4 and 6 is 12, and the LCM of 10 and 15 is 30. There are numerous ways for determining the least common multiples, just as there are for computing the greatest common divisors. One approach is to divide both numbers by their primes.To find at what time will both trains leave the station together again if both of them left the station together at 6:30 am:
If a train to New York City departs every 7 minutes and another to Boston departs every 6 minutes,The two trains then depart together after a time equal to the LCM of their individual intervalsLCM (7,6) = 42As a result, if they begin at the same time, they will depart at the same time every 42 minutes.If both trains left the station at 6.30 a.m., they will leave together again 42 minutes later, at 7.12 am.
Therefore, both trains will leave the station together again at 7:12 am if both of them left the station together at 6:30 am.
Know more about LCM here:
https://brainly.com/question/233244
#SPJ4
CAN SOMEONE HELP ME WUICK IM STUCK IN THE WASHER STEP BRO
Answers
Answer:
where is the problem.....
Our world has always been faced with the problem of discrimination. It is one of the most discussed topics nowadays and throughout history. In all countries there is most likely at least one type of discrimination that affects different groups of people. The definition of discrimination is the denial of opportunity or equal rights for a specific group of people that may be differentiated by things such as their religion, color of skin, or gender. Discrimination can be confused with other terms such as prejudice and stereotype. The world we live in has been struggling with this sensitive subject for as long as we have recorded. Stereotypes are images held in our minds in regards to certain racial or cultural groups, without consideration of whether the images held are true or false. Stemming from stereotypes is prejudice. The prejudicial attitude occurs when we prejudge a person, good or bad, on the basis that the stereotypes associated with the person or group being prejudged are true. Discrimination is the combination of the terms mentioned above, but involves actually acting out with unfair treatment, directing the action towards the person or group. Prejudice and discrimination do not just occur racially, but it is found among gender, religion, culture, and geographical background. Remember that prejudice is a result of attitude and discrimination is a result of action.
Many people believe discrimination has made big steps forward, but has it really? If it has, why do people still get turned down, receive hate mail, or get ridiculed simply because they differ from each other. I guess these are questions we must ask ourselves. I guess you could also ask yourself if you have ever called anybody a name, looked at them different or judged them when you did not even know them or understand them. You may be thinking “That is not discrimination,” but, in fact, it is.
\(\huge\mathcal{\fbox{\fbox\red{Hello}}}\)
\(\large\underline{\mathbb{AnSwEr}:}\)
\(\pink{ \rule{80pt}{100000pt}}\)
Which set of ordered pairs does not represent a function?
O{(-2,5), (0, -9), (8,-2), (7,4)}
O{(-3,4), (-5,4), (7, -3), (2, -9)}
O {(2, -9), (-5, -1), (-6, -3), (-5,7)}
O {(1, -8), (-9,-2), (-4,0), (4, -8)}
Answers
Step-by-step explanation:
{(2, -9), (-5, -1), (-6, -3), (-5,7)}
-5 appears twice ( this is not allowed for the function)
Determine the minimum sample size required when you want to be 95% confident that the sample mean is within two units of the population mean. assume a population standard deviation of 3.8 in a normally distributed population.
Answers
Minimum sample size (n) = 15
To determine the minimum sample size required, we can use the formula:
n = (Zα/2 * σ / E)^2
Where:
- n is the minimum sample size
- Zα/2 is the z-score at the 95% confidence level, which is 1.96
- σ is the population standard deviation, which is given as 3.8
- E is the maximum error we can tolerate, which is 2 units in this case
Substituting the values, we get:
n = (1.96 * 3.8 / 2)^2
n = 27.44
Rounding up to the nearest whole number, we get a minimum sample size of 28.
Therefore, we need to sample at least 28 individuals from the normally distributed population to be 95% confident that the sample mean is within two units of the population mean, assuming a population standard deviation of 3.8.
To determine the minimum sample size required for a 95% confidence level, we'll need to use the following formula:
n = (Z * σ / E)^2
where:
- n is the minimum sample size
- Z is the Z-score corresponding to the desired confidence level (1.96 for a 95% confidence level)
- σ is the population standard deviation (3.8 in this case)
- E is the margin of error (2 units in this case)
Step 1: Identify the values
Z = 1.96 (from the 95% confidence level)
σ = 3.8
E = 2
Step 2: Plug the values into the formula
n = (1.96 * 3.8 / 2)^2
Step 3: Calculate the result
n = (7.528 / 2)^2
n = (3.764)^2
n ≈ 14.15
Since the sample size must be a whole number, round up to the nearest whole number to ensure the desired level of confidence is achieved.
Minimum sample size (n) = 15
Learn more about standard deviation at: brainly.com/question/23907081
#SPJ11
2ℓ + 2w for ℓ = 5.7 and w = 6.2
Answers
Step-by-step explanation:
2(5.7) + 2(6.2)
11.4 + 12.4
23.8
Answer:
23.8
Step-by-step explanation:
2p + 2w = 2 * 5.7 + 2 * 6.2
= 11.4 + 12.4
= 23.8
Find the absolute maximum and minimum values of the function, subject to the given constraints. k(x,y)=−x2−y2 4x 4y; 0≤x≤3, y≥0, and x y≤6
Answers
For function k(x, y) = -x² - y² + 4x + 4y,
the absolute minimum is 0 and the absolute maximum is 6
For given question,
We have been given a function k(x, y) = -x² - y² + 4x + 4y
We need to find the absolute maximum and minimum values of the function, subject to the constraints 0 ≤ x ≤ 3, y ≥ 0, and x + y ≤ 6
First we find the partial derivative of function k(x, y) with respect to x.
⇒ \(k_x=-2x+4\)
Now, we find the partial derivative of function k(x, y) with respect to y.
\(\Rightarrow k_y=-2y+4\)
To find the critical point:
consider \(k_x=0\) and \(k_y=0\)
⇒ -2x + 4 = 0 and -2y + 4 = 0
⇒ x = 2 and y = 2
This means, the critical point of function is (2, 2)
We have been given constraints 0 ≤ x ≤ 3, y ≥ 0, and x + y ≤ 6
Consider k(0, 0)
⇒ k(0, 0) = -0² - 0² + 4(0) + 4(0)
⇒ k(0, 0) = 0
Consider k(3, 3)
⇒ k(3, 3) = -3² - 3² + 4(3) + 4(3)
⇒ k(3, 3) = -9 - 9 + 12 + 12
⇒ k(3, 3) = -18 + 24
⇒ k(3, 3) = 6
Therefore, for function k(x, y) = -x² - y² + 4x + 4y,
the absolute minimum is 0 and the absolute maximum is 6
Learn more about the absolute maximum and absolute minimum values of the function here:
brainly.com/question/16270755
#SPJ4
QUESTION 18 If f(x) = |x|2, then f'(0) = 0. O True O False QUESTION 19 The discontinuity of f(x) = O True O False x²-1 x-1 کے at x= 1 is removable.
Answers
Thus, the statement "The discontinuity of f(x) = x²-1 / x-1 at x= 1 is removable" is True.
Answer:
The given functions are f(x) = |x|2 and f(x) = x²-1 / x-1 .
The questions to be answered are: If f(x) = |x|2, then f'(0) = 0. True or False?
The discontinuity of f(x) = x²-1 / x-1 at x= 1 is removable.
True or False?
Solutions:
Let us consider the function f(x) = |x|2
In order to calculate the value of f'(0), we first need to calculate the derivative of the given function.
Let us do that.
f(x) = |x|2
Now, |x| = x, when x ≥ 0 and |x| = -x, when x < 0
Therefore, f(x) = |x|2 = x2,
when x ≥ 0 and f(x) = |x|2 = (-x)2 = x2, when x < 0
The given function is defined for all values of x in the domain and it is differentiable for all x in the domain.
Now, f(x) = x2
Let us find
f'(x)f(x) = x2
Applying the power rule of differentiation, we have
f'(x) = 2xThus, f'(0) = 0×2 = 0
Therefore, f'(0) = 0 is True.
Let us consider the function f(x) = x²-1 / x-1
To check whether the discontinuity of f(x) at x=1 is removable or not, we can check the limit of the function at x=1.
If the limit exists and it is finite, then the discontinuity is removable.
If the limit does not exist or it is infinite, then the discontinuity is not removable.
Now, f(x) = x²-1 / x-1
We can factorize the denominator x-1 and simplify the function
f(x) = x²-1 / x-1 = (x+1)(x-1) / (x-1) = (x+1)
Now, let us find the limit of the function as x approaches 1 from the left-hand side(LHL)
limx→1- f(x) = limx→1- (x+1) = 1+1 = 2
Now, let us find the limit of the function as x approaches 1 from the right-hand side
(RHL)limx→1+ f(x) = limx→1+ (x+1) = 1+1 = 2
Since the LHL and RHL of the function are equal and finite, the limit of the function exists and it is finite.
Therefore, the discontinuity of f(x) at x=1 is removable.
to know more about function discontinuity visit:
https://brainly.com/question/28914808
#SPJ11
The net of a solid figure is shown below.
Which calculation will give the total surface area of the solid figure?
06-4-4 square inches
04-6-6 square inches
06-4-4-4 square inches
04-6-6-6 square inches

Answers
Suppose each license plate in a certain state has three digits followed by three letters. The digits 4 and 5 are not used. So, there are 26 letters and 8 digits that are used. Assume that the letters and digits can be repeated. How many license plates can be generated using this format?
Answers
The required, there are 8998912 possible license plates that can be generated using this format.
Here, we have,
There are 8 digits that can be used for each of the three digits on the license plate, with two digits (4 and 5) that cannot be used.
Therefore, there are 8 choices for each of the three digits,
giving us 8 x 8 x 8 = 512 possible combinations for the digits.
Similarly, there are 26 letters that can be used for each of the three letters on the license plate.
Therefore, there are 26 choices for each of the three letters, giving us 26 x 26 x 26 = 17576 possible combinations for the letters.
Total number of license plates = number of choices for the digits x number of choices for the letters
= 512 x 17576
= 8998912
Therefore, there are 8998912 possible license plates that can be generated using this format.
Learn more about combination here:
brainly.com/question/13387529
#SPJ1
1) Ed invests $1,000 into a money market account that earns 8% annual interest compounded quarterly. How much money will
he have earned after 8 years?
Answers
The money market account earns 8/4 = 2% interest per quarter.
In one year, there are 4 quarters.
so, the formula to calculate the balance after 8 years is:
A = P (1 + r/n)^(nt)
where A is the final balance, P is the principal (initial investment), r is the annual interest rate, n is the number of times interest is compounded per year, and t is the number of years the money is invested for.
Substituting in the given values,
A = 1000 (1 + .02)^(4*8)
A = 1000 (1.02)^32
A = 1000 (1.8587)
A = 1858.7
So after 8 years, Ed will have earned $1858.7.
PLEASE HELP ME I ONLY HAVE TODAY TO COMPLETE THIS ),:
What is the radical form of each of the given expressions?

Answers
Answer:
1. 7\(\frac{1}{2}\) = \(\sqrt{7}\)
2. 4\(\frac{7}{2}\) = \(\sqrt{4} x^{7}\)
3. 7\(\frac{1}{4}\) = \(\sqrt[4]{7}\)
4. 4\(\frac{1}{7}\) = \(\sqrt[7]{4}\)
Step-by-step explanation:
Can you explain how to solve this problem?
(Please write in neat text to read clearly)
7.21 The number of customers, K, that shop at the neighborhood store in a day has the PMF Pk (k) ke k=0,1,2,... k! Independently of K, the number of items N that each customer purchases has the PMF n=
Answers
Once I have the PMF for N, I can explain how to use these PMFs to calculate various probabilities or expected values related to the number of customers and items purchased at the neighborhood store.
Let's break down the problem step by step.
The problem states that the number of customers, K, that shop at the neighborhood store in a day follows a probability mass function (PMF) given by Pk(k) = ke^(-k!) for k = 0, 1, 2, ...
We are also given that the number of items, N, that each customer purchases has its own PMF, which is not specified in your question. To solve the problem completely, we need the PMF for N as well. Please provide the PMF for N so that I can proceed with the solution.
Once I have the PMF for N, I can explain how to use these PMFs to calculate various probabilities or expected values related to the number of customers and items purchased at the neighborhood store.
Learn more about probabilities here
https://brainly.com/question/25839839
#SPJ11
PLEASE HURRY TIME LIMIT 30 POINTS
If ∆is a right triangle AB is 27, BC is 36, and AC is 45, which of the following can be used to find the measure of ∠? Select all that apply.
a.=3645
b.=2745
c.=3645
d.=2745
e.=3627
f.=2736
Answers
Answer:
see the answersStep-by-step explanation:
to understand thisyou need to know abouttrigonometrytips and formulas:sin=opp/hypoCos=adj/hypotan=opp/adjlet's solve:according to the question
\( b)\sin( \theta) = \frac{27}{45} \)
according to the question
\( c)\cos( \theta) = \frac{36}{45} \)
according to the question
\( f)\tan( \theta) = \frac{27}{36} \)

MODELING WITH MATHEMATICS A discounted amusement park ticket costs $12.95 less than the original price p.
Write and solve an equation to find the original price.
It's crazy fun at
COASTER MADNESS
Discounted Price $443
ADMIT ONE GUEST
Equation:
= 44
The original price of the ticket is $
Answers
we conclude that the original price of the ticket is $57.25
How to find the original price of the ticket?We know that the discounted price is $12.95 less than the original price P, and the discounted price is $44.30.
Then the original price is $12.95 more than the discounted price, this means that we just need to solve the addition problem:
P = $44.30 + $12.95 = $57.25
In this way, we conclude that the original price of the ticket is $57.25
If you want to learn more about addition:
https://brainly.com/question/25421984
#SPJ1
The population of a village 1000 one year ago. The present population is 1021. find the population growth rate
Answers
Answer:
21 is increase in population