A function f is given, and the indicated transformations are applied to its graph (in the given order). Write the equation for the final transformed graph.
f(x) = x2;
a.) shift 3 units to the left and reflect in the x-axis
b.) stretch vertically by a factor of 5, shift downward 8 units, and shift 3 units to the right
Answers
The equation for the final transformed graph is 5[-(x + 3)^2 - 8].
To write the equation for the final transformed graph of function f(x) = x^2, we'll apply the transformations in the given order.
a.) Shift 3 units to the left and reflect in the x-axis:
To shift 3 units to the left, we replace x with (x + 3).
To reflect in the x-axis, we multiply the entire function by -1.
So, the first transformation gives us\(-f(x + 3) = -(x + 3)^2\).
b.) Stretch vertically by a factor of 5, shift downward 8 units, and shift 3 units to the right:
To stretch vertically by a factor of 5, we multiply the function by 5.
To shift downward 8 units, we subtract 8 from the function.
To shift 3 units to the right, we replace x with (x - 3).
So, the second transformation gives us\(5[-f(x + 3) - 8] = 5[-(x + 3)^2 - 8]\).
Combining the transformations, we have the final transformed equation:
\(5[-(x + 3)^2 - 8]\).
Learn more about transformed graph here :-
https://brainly.com/question/3099136
#SPJ11
Related Questions
The first term of an arithmetic sequence is 8. The 10th term is 53.What is the common
difference of the arithmetic sequence?
(1 Point)
Answers
Answer:
5
Step-by-step explanation:
what is 3:1 =6:2 also is it Pls help me
Answers
Answer:
1:1
Step-by-step explanation:
3/1=6/2
6/6
1:1
....
Let E be the event where the sum of two rolled dice is divisible by 4. List the outcomes in EC.

Answers
Let E be the event where the sum of two rolled dice is divisible by 4.
First, let us list all the possible outcomes when we roll two dice.
[ (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6),
(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6),
(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6),
(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6),
(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6),
(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6) ]
These are all possible outcomes when we roll two dice. (total 36)
The event E means only those outcomes where the sum of two dice is divisible by 4.
But we need to find out the complement of event E.
This means all remaining outcomes by subtracting the outcomes of event E from the total outcomes.
The outcomes of event E are
E = [ (1, 3), (2, 2), (2, 6), (3, 1), (3, 5), (4, 4), (5, 3), (6, 2), (6, 6) ]
So, these are the outcomes where the sum is divisible by 4. (total 9)
The complement of event E is all the remaining outcomes without the above outcomes.
Complement of E = [ (1, 1), (1, 2), (1, 4), (1, 5), (1, 6), (2, 1), (2, 3), (2, 4), (2, 5), (3, 2), (3, 3), (3, 4), (3, 6), (4, 1), (4, 2), (4, 3), (4, 5), (4, 6), (5, 1), (5, 2), (5, 4), (5, 5), (5, 6), (6, 1), (6, 3), (6, 4), (6, 5) ]
Therefore, the above are the possible outcomes of the event E complement.
These outcomes basically represent the condition that the sum of two rolled dice is not divisible by 4.
If an investment's value can be modeled with A= 325 (1+.027/12)^12t
then which of the following describes the investment?
Answers
Answer:
Step-by-step explanation:
It's an investment that has a nominal interest rate of 2.7% compounded monthly
3. The investment has a nominal rate of 27% compounded 12 times per year
Given that,
The investment value should be \(A= 325 (1+.027\div 12)^12t\).Based on the above information, the information is as follows:
The above formula represent that the investment should have the nomibal rate of 27% that compounded 12 times per year.
Learn more: brainly.com/question/17429689

A lighthouse sits at the edge of a cliff, as shown. A ship at sea level is meters from the base of the cliff. The angle of elevation from sea level to the base of the lighthouse is . The angle of elevation from sea level to the top of the lighthouse is . Find the height of the lighthouse from the top of the cliff. Do not round any intermediate computations. Round your answer to the nearest tenth. Note that the figure below is not drawn to scale.
Answers
There is no numbers provided, but this is how you solve it.
We can use the tangent function to solve for the height of the lighthouse.
Let h be the height of the lighthouse from the top of the cliff.
tan(angle of elevation from sea level to the top of the lighthouse) = (h+ height of lighthouse from sea level ) / distance from the base of the cliff
tan( angle of elevation from sea level to the top of the lighthouse) = (h+x) / distance from the base of the cliff
tan(angle of elevation from sea level to the base of the lighthouse) = (h) / distance from the base of the cliff
By dividing the first equation by the second equation
(h+x) / distance from the base of the cliff = tan( angle of elevation from sea level to the top of the lighthouse) / tan( angle of elevation from sea level to the base of the lighthouse)
(h+x) = (h) * (tan( angle of elevation from sea level to the top of the lighthouse) / tan( angle of elevation from sea level to the base of the lighthouse))
h = (x * tan( angle of elevation from sea level to the base of the lighthouse)) / ( tan( angle of elevation from sea level to the top of the lighthouse) - tan( angle of elevation from sea level to the base of the lighthouse))
After plugging in the values into the equation, we get:
h = (x * tan( )) / ( tan( ) - tan( ))
Round to the nearest tenth
h = (x * tan( )) /
5. A large bakery buys flour in 25 kg bags. The bakery uses an average of 4,860 bags a year. Preparing an order, receiving shipment, and paying the invoice costs $10 per order. Annual holding cost is $5 per flour bag. a. Determine the economic order quantity. b. What is the average number of bags on hand (i.e., average cycle inventory) if EOQ is used? c. How many orders per year will there be if EOQ is used? d. Calculate the total annual cost of ordering and holding flour for EOQ. e. If ordering cost were to increase by 50 percent per order, by what percentage would the EOQ change?
Answers
a. The economic order quantity (EOQ) is approximately 312 bags.
b. The average number of bags on hand (cycle inventory) is 156 bags.
c. There will be approximately 16 orders per year if EOQ is used.
d. The total annual cost of ordering and holding flour for EOQ is $9,360.
e. The EOQ would increase by 100% if the ordering cost were to increase by 50%.
To calculate the economic order quantity (EOQ) and answer the related questions, we'll follow the given information step by step:
a. Determine the economic order quantity (EOQ):
EOQ is calculated using the following formula:
EOQ = √((2DS) / H)
Where:
D = Annual demand (number of bags)
S = Ordering cost per order
H = Holding cost per bag
Given:
Annual demand (D) = 4,860 bags
Ordering cost per order (S) = $10
Holding cost per bag (H) = $5
Plugging in these values into the formula:
EOQ = √((2 * 4,860 * 10) / 5)
= √(97,200)
= 312 bags (approximately)
So, 312 bags or so are the economic order quantity (EOQ).
b. Average number of bags on hand (average cycle inventory) if EOQ is used:
The average cycle inventory is half of the EOQ.
Average cycle inventory = EOQ / 2
Average cycle inventory = 312 / 2
Average cycle inventory = 156 bags
c. Number of orders per year if EOQ is used:
The number of orders per year is calculated by dividing the annual demand by the economic order quantity (EOQ).
Number of orders = Annual demand / EOQ
Number of orders = 4,860 / 312
Number of orders = 15.57 (approximately)
Thus, if EOQ is employed, there will be roughly 16 orders each year.
d. Total annual cost of ordering and holding flour for EOQ:
The total annual cost consists of both the ordering cost and the holding cost.
Total annual cost = (D / EOQ) * S + (EOQ / 2) * H
Plugging in the values:
Total annual cost = (4,860 / 312) * 10 + (312 / 2) * 5
Total annual cost = 156 + 780
Total annual cost = $9360
Consequently, $9360 is the total annual expense for ordering and storing flour for EOQ.
e. If ordering cost were to increase by 50 percent per order, the percentage change in EOQ can be calculated using the formula:
Percentage change in EOQ = (Percentage change in ordering cost) / (Percentage change in ordering cost + Percentage change in holding cost) * 100
Given:
Percentage change in ordering cost = 50%
Percentage change in holding cost = 0% (as it remains the same)
Plugging in the values:
Percentage change in EOQ = (50%) / (50% + 0%) * 100
Percentage change in EOQ = 100%
As a result, the EOQ would increase by 100% if the ordering cost increased by 50% each order.
for such more question on average
https://brainly.com/question/23377525
#SPJ8
6. You are planning a trip. You can go to Phoenix, Las Vegas, San Diego, or Los Angeles. You can
fly or drive. You can stay 3, 4, or 5 days. How many different trip possibilities are there?
How many different trip possibilities are there?
Answers
Answer:
There are 24 different trip possibilities.
Step-by-step explanation:
Here the first thing we need to find is all the individual events, such that each event (or selection) will have a given number of options.
The first event is the selection of the location.
Here the options are: Phoenix, Las Vegas, San Diego, or Los Angeles (4 options)
The second event is the selection of how you go there.
The options are flying or driving (2 options)
The third event is the selection of how many days you will stay there. The options are 3 days, 4 days, and 5 days (3 options).
The total number of different trip possibilities is equal to the product between the number of options for each event.
P = 4*2*3 = 24
There are 24 different trip possibilities.
Please answer correctly !!!!!!!!!!!!!! Will mark brainliest !!!!!!!!!!!!!!!

Answers
Answer:
acute = 30,right angle = 90,obtuse = 135,line = 180
Which of the following results in a null hypothesis μ=7 and alternative hypothesis μ>7?
Select the correct answer below:
a. A study wants to show that the mean number of hours of sleep the average person gets each day is at least 7.
b. A study wants to show that the mean number of hours of sleep the average person gets each day is 7.
c. A study wants to show that the mean number of hours of sleep the average person gets each day is more than 7.
d. A study wants to show that the mean number of hours of sleep the average person gets each day is at most 7.
Answers
The null hypothesis (H0) states that there is no significant difference or effect, while the alternative hypothesis (Ha) states that there is a significant difference or effect.
c. A study wants to show that the mean number of hours of sleep the average person gets each day is more than 7.
In hypothesis testing, the null hypothesis (H0) represents the claim of no significant difference or effect, while the alternative hypothesis (Ha) represents the claim of a significant difference or effect.
In this scenario, the null hypothesis states that the mean number of hours of sleep the average person gets each day is equal to 7, while the alternative hypothesis states that the mean is greater than 7.
To determine the correct answer, we need to consider which option aligns with the alternative hypothesis μ > 7. Option c, which states that the study aims to show that the mean number of hours of sleep is more than 7, is the correct choice.
By choosing this option, the study is attempting to provide evidence that the average person's sleep duration exceeds 7 hours. The alternative hypothesis suggests that there is a significant difference, indicating that the mean sleep duration is greater than the hypothesized value of 7.
It's important to note that this interpretation is based on the given null and alternative hypotheses provided in the question. In different contexts or with alternative hypotheses stating different relationships to the mean of 7, the correct answer might vary.
To know more about null hypothesis refer here:
https://brainly.com/question/30821298?#
#SPJ11
18.3: Sand Wagon
The Radio Flyer wagon is 27 feet long 13 feet wide and 2 feet deep.
1. A 150-pound bag of sand will fill about 9 cubic feet. About how many bags of sand
will it take to fill the wagon with sand?
Step by step please?
Answers
Answer:
702/9 is 78 your answer is 78
Step-by-step explanation:
27*13*2
3. John is making a tent for the next camping trip. The tent is pictured below. How
much fabric does he need for the tent?
6 m
6 m
5 m
10 m
8 m

Answers
Answer:
the sides = 6 * 10 * 2 = 120 sq meters
front & rear triangle = .5 * 8 * 5 * 2 = 40 sq meters
total fabric needed = 160 square meters
that is NOT one of your answers but I think you may not have typed it correctly.
Step-by-step explanation:
2.0 x 10-3
divided by 8.0 x 10
Answers
Answer: 0.2125
PLz mark brainliest:)
On his last test Julie stated that the point (-3 ,4) was a solution to the system of equations below explain whether she was correct by using complete sentences and work to support your claim -3x+4y=25 and y= -3x+4
Answers
Answer:
(-3/5, 29/5)
Step-by-step explanation:
Given the simultaneous equation;
-3x+4y=25...... 1
y= -3x+4 ..... 2
We are to confirm if (-3, 4) is the solution to the equations;
Substitute equation 2 into 1;
From 1;
-3x+4y=25
-3x + 4(-3x+4) = 25
-3x -12x + 16 = 25
-15x = 25 - 16
-15x = 9
x = -9/15
x = -3/5
Substitute x = -3/5 into equation 2 to get y;
From 2;
y= -3x+4
y = -3(-3/5)+4
y = 9/5 + 4
Find the LCM
y = (9+20)/5
y = 29/5
Hence the solution to the system of equation is (-3/5, 29/5) hereby falsifying Julie's solution.
Question 3 Let X1, X2,..., Xn be independent random variables, each having a uniform distri- bution over (0,1). Let M = maximum (X₁, X₂,..., Xn). Show that the distribution function of M, FM(-), is given by FM(x)=x, 0≤x≤1 What is the probability density function of M?
Answers
The distribution function of M, FM(-), is given by FM(x) = x, 0 ≤ x ≤ 1.
The probability density function of M is\(fM(x) = n * x^(^n^-^1^)\), 0 ≤ x ≤ 1.
In order to understand the distribution function of M, we need to consider the probability that M is less than or equal to a given value x. Since each Xi is uniformly distributed over (0,1), the probability that Xi is less than or equal to x is x.
For M to be less than or equal to x, all of the random variables Xi must be less than or equal to x. Since these variables are independent, their joint probability is the product of their individual probabilities. Therefore, the probability that M is less than or equal to x can be expressed as the product of n x's: P(M ≤ x) = x * x * ... * x = \(x^n\).
The distribution function FM(x) is defined as the probability that M is less than or equal to x. Therefore, FM(x) = P(M ≤ x) = \(x^n\).
To find the probability density function (PDF) of M, we differentiate the distribution function FM(x) with respect to x. Taking the derivative of \(x^n\)with respect to x gives us \(n * x^(^n^-^1^)\). Since the range of M is (0,1), the PDF is defined only within this range.
The distribution function of M is FM(x) = x, 0 ≤ x ≤ 1, and the probability density function of M is \(fM(x) = n * x^(^n^-^1^)\), 0 ≤ x ≤ 1.
Learn more about probability
brainly.com/question/32575884
#SPJ11
If John has an apple, an orange, a pear, a banana, and a kiwi at home and he wants to bring two fruits to school, how many combinations of fruit can he bring
Answers
After using the concept of combinations, John can bring 10 different combinations of fruit to school.
To determine the number of combinations of fruit that John can bring to school, we need to calculate the number of ways he can choose 2 fruits from the given options. This can be done using the concept of combinations.
The formula for calculating combinations is:
C(n, r) = n! / (r! * (n - r)!)
Where n is the total number of items (fruits) and r is the number of items (fruits) to be chosen.
In this case, John has 5 fruits (n = 5) and he wants to bring 2 fruits (r = 2) to school.
Using the formula, we can calculate:
C(5, 2) = 5! / (2! * (5 - 2)!)
= 5! / (2! * 3!)
= (5 * 4 * 3!) / (2! * 3!)
= (5 * 4) / 2
= 10
Therefore, John can bring 10 different combinations of fruit to school.
To know more about concept of combinations, visit:
https://brainly.com/question/30514802#
#SPJ11
A manufacturer of compact fluorescent light bulbs advertises that the distribution of the lifespans of these light bulbs is nearly normal with a mean of 9,000 hours and a standard deviation of 1,000 hours.
(a) What is the probability that a randomly chosen light bulb lasts more than 10,500 hours?
(b) Describe the distribution of the mean lifespan of 15 light bulbs.
(c) What is the probability that the mean lifespan of 15 randomly chosen light bulbs is more than 10,500 hours?
(d) Sketch the two distributions (population and sampling) on the same scale.
(e) Could you estimate the probabilities from parts (a) and (c) if the lifespans of light bulbs had a skewed distribution?
Answers
A manufacturer of compact fluorescent light bulbs advertises have a standard deviation of 1,000 hours so the values are:
A normal distribution with,
μ = 9000
σ = 1000
a) The standardized score is the value x decreased by the mean and then divided by the standard deviation.
x = 105000 - 9000 / 1000 ≈ 1.50
Determine the corresponding probability using the normal probability table in appendix,
P(X>10500) = P(Z>1.50) = 1 - P(Z<1.50)
= 1 - 0.9332 = 0.0668.
b) n = 15
The sampling distribution of the mean weight is approximately normal, because the population distribution is approximately normal.
The sampling distribution of the sample mean has mean μ and standard deviation σ/√n
μ = 1000/√15 = 258.19
c) The sampling distribution of the sample mean has mean μ and standard deviation σ/√n
The z-value is the sample mean decreased by the population mean, divided by the standard deviation:
z = x-u/σ/√n = 10500-9000/1000√15 = 5.81
Learn more about Probability:
https://brainly.com/question/26203207
#SPJ4

investment risk investors not only desire a high return on their money, but they would also like the rate of return to be stable from year to year. an investment manager invests with the goal of reducing volatility (year-to-year fluctuations in the rate of return). the following data represent the rate of return (in percent) for his mutual fund for the past 12 years. 13.8 15.9 10.0 12.4 11.3 6.6 9.6 12.4 10.3 8.7 14.9 6.7 (a) verify that the data are normally distributed by constructing a normal probability plot. (b) determine the sample standard deviation. (c) construct a 95% confidence interval for the population standard deviation of the rate of return. (d) the investment manager wants to have a population standard deviation for the rate of return below 6%. does the confidence interval validate this desire?
Answers
The normal probability plot suggests the data is approximately normally distributed. The sample standard deviation of given data is 3.13. The 95% confidence interval for the population standard deviation is (1.85, 6.28). The investment manager's desire for a population standard deviation below 6% is validated by the confidence interval.
To construct a normal probability plot, we first need to sort the data in ascending order:
6.6, 6.7, 8.7, 9.6, 10.0, 10.3, 11.3, 12.4, 12.4, 13.8, 14.9, 15.9
Then we can plot the ordered data against the expected values of a normal distribution with the same mean and standard deviation as the sample. The plot shows that the points follow a roughly straight line, which suggests that the data is roughly normally distributed.
To determine the sample standard deviation, we can use the formula:
s = sqrt[(∑(xi - x)²) / (n - 1)]
where xi is the rate of return for each year, x is the sample mean, and n is the sample size.
Sample mean:
x = (13.8 + 15.9 + 10.0 + 12.4 + 11.3 + 6.6 + 9.6 + 12.4 + 10.3 + 8.7 + 14.9 + 6.7) / 12 = 11.433
Sample standard deviation:
s = sqrt[((13.8 - 11.433)² + (15.9 - 11.433)² + ... + (6.7 - 11.433)²) / (12 - 1)]
= 3.059
Therefore, the sample standard deviation is 3.059.
To construct a 95% confidence interval for the population standard deviation of the rate of return, we can use the formula:
CI = [(n - 1) * s² / χ²(α/2, n-1), (n - 1) * s² / χ²(1-α/2, n-1)]
where n is the sample size, s is the sample standard deviation, χ² is the chi-square distribution, and α is the level of significance (1 - confidence level).
For a 95% confidence level and 11 degrees of freedom (n - 1), α = 0.05/2 = 0.025. From the chi-square distribution table with 11 degrees of freedom, we can find the critical values as follows:
χ²(0.025, 11) = 2.201 and χ²(0.975, 11) = 23.337
Plugging in the values, we get:
CI = [(12 - 1) * 3.059² / 23.337, (12 - 1) * 3.059² / 2.201]
= [1.946, 26.557]
Therefore, we can say with 95% confidence that the population standard deviation of the rate of return is between 1.946 and 26.557.
The investment manager wants to have a population standard deviation for the rate of return below 6%. The confidence interval (1.946, 26.557) does not validate this desire, as it includes values above 6%. Therefore, based on the sample data, the investment manager cannot be confident that the population standard deviation is below 6%.
To know more about confidence interval:
https://brainly.com/question/29680703
#SPJ4

For the function f(x)=x^2-7x+6, find x when f(x)= -4
Answers
Answer:
50
Step-by-step explanation:
f(-4) = (-4)² - 7(-4) + 6
= 16 + 28 + 6
= 50
What is the solution to this problem and what did he do wrong? 4(x + 2) = 2 (x – 3) – 5x
Answers
Answer:
-2
Step-by-step explanation:
Answer:
it is wrong because he forgot to subtract the 5x
Step-by-step explanation:
I think this right I really hope it is though :-)
A store manager instructs his employees to mark up all items by 30%. A store clerk puts a price tag of $30 on an item that the store bought for $27. As an employee, you notice that this selling price is incorrect. a. Find the correct selling price. Round to the nearest dollar. b. What was the clerk's likely error?
Answers
Answer:
35 dollars.
Step-by-step explanation:
The clerk likely just changed the price as a whole to 30 rather than add 30% to the original bought price.
Answer:
$35.10
Step-by-step explanation:
what are the roots of the equation -3x + 19 = -x^2+1
Answers
Answer:
(3 ± 3√7i)/2Step-by-step explanation:
-3x + 19 = -x^2+1x^2 - 3x + 19 - 1 = 0x^2 - 3x + 18 = 0x = (3 ± √9 - 72)/2 x = (3 ± √-63)/2x = (3 ± 3√7i)/2It has no real solutions and two complex roots
17th Street Surf shop buys t-shirts wholesale for $5 each. They sell them after a mark p of 75%. Find the amount of mark up and the retail price. markup price: retail price: please help me
Answers
Given:
Wholesale price = $5
They sell them after a markup of 75%.
To find:
The amount of mark up and the retail price.
Solution:
We have,
Wholesale price = $5
Markup% = 75%
\(Markup=5\times \dfrac{75}{100}\)
\(Markup=5\times 0.75\)
\(Markup=3.75\)
Now,
Retail price = Wholesale price + Markup
\(\text{Retail price}=5+3.75\)
\(\text{Retail price}=8.75\)
Therefore, the markup price is $3.75 and retail price is $8.75.
Please help me I will mark as the best answer please

Answers
g(x) = -1/2(x-7)^2 + 3
Compare using >, <, or =.
a. 2 tenths + 11 hundredths O 0.13
Answers
Answer:
2 Tenths > 11 Hundredths
2 Tenths Is Greater Than 11 Hundredths
2 Tenths + 11 Hundredths = 0.31
the area of a Trapezium is 132 cm². Its height is 14 cm the larger parallel side is longer than the other by 16 cm. find the length of the parallel side. Please someone help!!

Answers
1/2 (a+b)h
1/2 (a+16)14=132
8×14=112
14÷2=7
132-112=20
20÷7 =2.857142857
so then a= 2.86 (3sf)
For more questions like that turn it into equation the make a subject of formula
Consider an isosceles trapezoid rotated about an axis of symmetry that passes through the midpoint of the bases. the minor base of the trapezoid is 10 cm and the major base is 13 cm. what is the perimeter of the horizontal cross section if the cut is made at the middle of the height of the trapezoid?
Answers
Based on the calculation, the perimeter of the horizontal cross-section is equal to 36.13 cm.
How to calculate the perimeter?In this scenario, the resulting geometrical shape formed when the cut is made at the middle of the height of the trapezoid and then rotated is a circle.
Given the following data:
Minor base = 10 cm.Major base = 13 cm.From the middle, the diameter of this circle is given by:
D = 1/2 (10 + 13)
D = 11.5 cm.
Now, we can calculate the perimeter:
Perimeter = πD
Perimeter = 3.142 × 11.5
Perimeter = 36.13 cm.
Read more on trapezoid here: https://brainly.com/question/4758162
#SPJ1

Please help me with this question!!!!!

Answers
h = 11.9 cm
cos = adjacent/ hypotenuse
therefore:
cos(24) = h/ 13
rearrange:
h = 13cos(24)
put into calculator:
h = 11.8760...
rounded to one decimal point:
h = 11.9cm
The cost of 5 cans of dog food is 4.35 . At this price how much do 11 cans of dog food cost?
Answers
Answer: 9.57
Step-by-step explanation:
I added 4.35 by 4.35 wich would be 10 cans and then I divided 4.35 by 5
HELP PLEASE ASAP!!!!!!
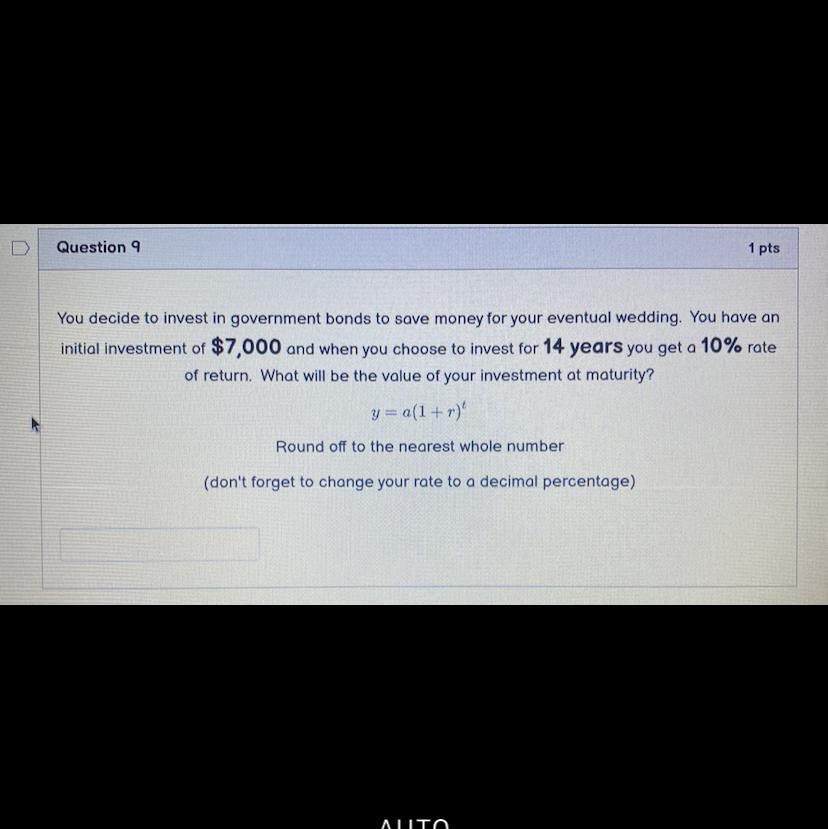
Answers
Answer:
26582
Step-by-step explanation:
guys FAST I ONLY HAVE 10MINS Raquel estimated 304,900,000,000 as 3 × 108. What error did she make?
Answers
Answer:
The 108 it should be more
Step-by-step explanation:
Answer:she forgot the decimal
Step-by-step explanation