A pie is split into 3 equally sized
pieces.
Each piece has an area of 79 in?
What is the total area of the pie?
Answers
the total area of the pie is 237
Related Questions
Georgia needs to buy some cheese. An 8-ounce package of
cheddar cheese costs $3.50. A 12-ounce package of cheddar
cheese costs $5.25. Which is the better buy? How many cents
per ounce cheaper is the better buy?
Answers
Answer:
neither buy is better, both buys are $2.28571428/ounce
f(x)=x² what is g(x)

Answers
Answer:
C) \(g(x) = -x^2 - 3\)
Step-by-step explanation:
The function has been reflected in the x-axis, so -f(x)
then translated by 3 units down, so -f(x) - 3
Therefore, \(g(x) = -x^2 - 3\)
4 divided by the sum of h and 7 using fraction
Answers
Answer:
4/5+7
or
4
_____
h+7
Two chicken coops are to be built adjacent to one another from 120 ft of fencing.
(a) What dimensions should be used to maximize the area of an individual coop?
The dimensions that would maximize the area of an individual coop are __ ft by __ ft.
(b) What is the maximum area of an individual coop?
The maximum area of an individual coop is __ ft^2.

Answers
The dimensions that would maximize the area of an individual coop are Xft by Y ft.
The maximum area of an individual coop is xy ft^2.
How to find the area of a rectangular shapeTo find the area of a rectangular shape, you simply need to multiply its length by its width. Here's the formula:
Area = Length × Width
Length (L) and Width (W) are the two perpendicular sides of the rectangle.
In the coop, we have the length of an individual area to be x, and the width = y
Hence area = x * y
Read more on area of a shape here:https://brainly.com/question/16501078
#SPJ1
i will give Brainiest if you are right

Answers
Answer:
H is the answer because 15/32 is the largest so it is in the back
Answer:
J. \(\frac{9}{32}, \frac{5}{16},\frac{3}{8},\frac{7}{16},\frac{15}{32},\frac{1}{2}\)
Step-by-step explanation:
7/16 = .4375
1/2 = .5
3/8 = .375
9/32 = .28125
5/16 = .3125
15/32 = .46875
let s(t) be the position of a particle in meters after t seconds. give the best approximate for the instantaneous velocity at 8 seconds. use this to approximate the position of the particle aftter 10 seconds.
Answers
The instantaneous velocity of the particle at 8 seconds is approximately the change in position over the change in time, or\(s(8+Δt) - s(8) / Δt\). If we use Δt = 0.1, then the instantaneous velocity is approximately s(8.1) - s(8) / 0.1. The approximate position of the particle after 10 seconds is then s(8) + (10-8) * (s(8.1) - s(8) / 0.1).
The instantaneous velocity of a particle is defined as the change in position over the change in time. This can be represented by the equation \(s(t+Δt) - s(t) / Δt\). Here, s(t) is the position of the particle at time t, and t is a small change in time. To approximate the instantaneous velocity at 8 seconds, we can use Δt = 0.1. This gives us an equation of s(8+0.1) - s(8) / 0.1. This equation gives us the velocity at 8 seconds. To approximate the position of the particle after 10 seconds, we can use the equation s(8) + (10-8) * (s(8.1) - s(8) / 0.1). This equation gives us an approximate position of the particle after 10 seconds, using the change in position over the change in time. This equation gives us a good approximation of the position of the particle after 10 seconds, given the information about the particle's position at 8 seconds.
Learn more about time here
https://brainly.com/question/28050940
#SPJ4
ered
Perform the following calculation. Report your answer using the correct number of significant
figures.
(6.45) (4.89)+8.1
OA. 39.64
OB. 39.6
OC. 40
OD. 39.641
Answers
The result of the calculation of the expression is 39.6, to three significant figures.
option B.
What is the simplification of expression?Simplification of an algebraic expression or any mathematical expression can be defined as the process of writing an expression in the most efficient and compact form without changing the actual meaning of the expression.
The given expression is;
(6.45) (4.89) + 8.1
The given expression is simplified as follows;
(6.45) (4.89) + 8.1
solve the bracket first;
= ( 6.45 x 4.89) + 8.1
= 31.54 + 8.1
now, do the addition operation;
= 31.54 + 8.1
= 39.64
The original numbers were given in three significant figures, so our final answer must be in 3 significant figures as well.
= 39.6 ( 3 s.g.f)
Learn more about significant figures here: https://brainly.com/question/24491627
#SPJ1
Given m∠14+m∠3=180° . Which lines are parallel, if any must be parallel, based on the given information? a∥b by the converse of the alternate interior angles theorem. c∥d by the converse of the corresponding angles theorem. a∥b by the converse of the same-side interior angles theorem. Not enough information to make a conclusion.
Answers
Answer:
c∥d by the converse of the corresponding angles theorem.
Step-by-step explanation:
The ratio of the heights of two similar pryramids is 2:5 and the volume of the smaller pyramid is 100 cubic feet. Find the volume of the larger pyramid.
Answers
The ratio of the heights of two similar pryramids is 2:5 and the volume of the smaller pyramid is 100 cubic feet. Find the volume of the larger pyramid.
Remember that
If two figures are similar the ratio of correspondig sides is proportional, and this ratio is called the scale factor
and
the ratio of their volumes is equal to the scale factor elevated to the cubic
so
In this problem
the scale factor is 2.5
therefore
Let
V -----> volume of the larger pyramid
so
V/100=(2.5)^3
V=100*(2.5^3)
V=1,562.5 ft3a right triangle is shownwhich angle measure is closet to x

Answers
We know that
\(\cos (x)=\frac{20}{24}\)Solving for x,
\(\begin{gathered} x=\cos ^{-1}(\frac{20}{24}) \\ \Rightarrow x=33.56 \end{gathered}\)x is aproximately 33.56
When the correlation between x and y is zero, what is the best prediction of a y score that can be made from a given x score?
Answers
Answer:
The mean of y
Step-by-step explanation:
In statistics, correlation is the degree of the linear relationship between two variables. The correlation coefficient is the numerical measure of the linear relationship of two variables, It is measured in the range -1 to 1. When the coefficient is negative, the variables are said to have a negative correlation, while it is a positive correlation or have a strong linear relationship if the correlation coefficient is positive.
When the correlation coefficient is zero, both variables have no linear relationship and the best predictions of each variable would be the mean.
evaluate the following 10+4(3+2)+5+(12÷6)
Answers
Answer:
37
Step-by-step explanation:
easy! plz help me tho
In a survey, the wording of the questions can introduce
Validity
Randomness
Bias
Uniformity
Answers
Answer:
bias
Step-by-step explanation:
the wording of the question may be misleading. the way the question is phrased influences the way the person who is being surveyed answers.
The wording of the questions can introduce (C) Bias.
What are bias questions?A question that is worded or expressed in a way that affects the respondent's opinion is considered biased. Such inquiries could offer details that influence a respondent's perspective on the topic.What are the types of bias?Bias in selection- When a sample is used in research that does not accurately reflect the larger population, selection bias arises. Aversion to Loss - People with loss aversion, which is a widespread human tendency, dislike losing more than they enjoy winning.Anchoring Bias. Framing Bias.Learn more about Bias brainly.com/question/3749477 here
#SPJ2
which expression is equivalent to the given polynomial expression? (9mn-19m^4n)-(8m^2+12m^4n+9mn)
A. -31m^4n+18mn-8m^2
B. -7m^4n+8m^2
C. -7m^4n+18mn-8m^2
D. -31m^4n-8m^2
Answers
9514 1404 393
Answer:
D. -31m^4n-8m^2
Step-by-step explanation:
Eliminate parentheses by distributing the minus sign. Then collect terms:
(9mn-19m^4n)-(8m^2+12m^4n+9mn) = 9mn -19m^4n -8m^2 -12m^4n -9mn
= m^4n(-19 -12) +mn(9 -9) +m^2(-8)
= -31m^4n -8m^2 . . . . . matches choice D
Answer this please its about finding volumes

Answers
Answer:
Step-by-step explanation:
volume = 696.56 in3
volume = 22,824.77 ft3
volume = 60,074.09 yd3
its all in order hope this helps :)
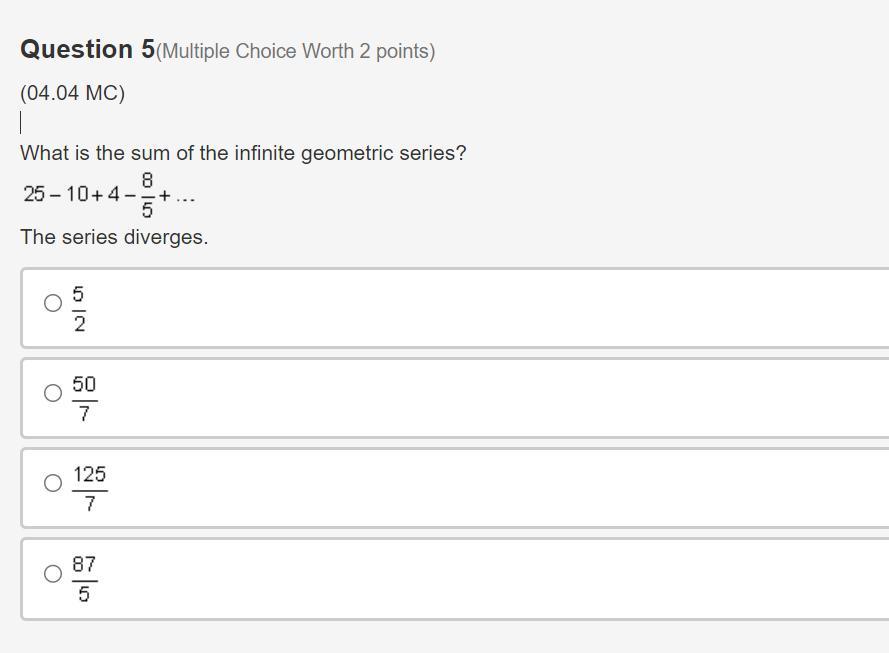
URGENT 50 POINTS + BRAINLY
What is the sum of the infinite geometric series?
25 minus 10 plus 4 minus eight fifths plus continuing
The series diverges.
five halves
fifty sevenths
one hundred twenty-five sevenths
eighty-seven fifths
Answers
Answer: \(C. \frac{125}{7}\)
Step-by-step explanation:
1. Find the sum of the infinite geometric sequence:
\(S = \frac{125}{7}\)
2. Find the correct option:
C
Molly deposits $1685 in an account that earns 3.5% interest
compounded annually. Write a function represent the situation where t is the time in years.
Answers
Answer:
1685 x 1.035^t
Step-by-step explanation:
compound interest formula:
initial x 1 ± percentage multiplier ^years. (time)
Solve the inequality:
8+4≥12
Answers
Answer:
I think it would be x<5
Step-by-step explanation:
hope this helps if not let me know have a blessed day
Simplify express your answer as a single term without a denominator cd3•c-5d-2
Answers
The simplified expression is d/ c⁴.
To simplify the expression cd³ c⁻⁵ x d⁻², we can combine the variables with the same base (c and d) by adding their exponents:
Using the property of exponents as
Product Rule:When multiplying two exponential expressions with the same base, you can add the exponents. This can be expressed as follows:
aᵇ x aⁿ= aᵇ⁺ⁿ
Quotient Rule:When dividing two exponential expressions with the same base, you can subtract the exponents. This can be expressed as follows:
aᵇ / aⁿ= aᵇ⁻ⁿ
So, cd³ c⁻⁵ x d⁻²
= c¹⁻⁵ x d³⁻²
= c⁻⁴ x d¹
= dc⁻⁴
Again from the property of exponents
a⁻ᵇ = 1/aᵇ
So, dc⁻⁴
= d/ c⁴
Therefore, the simplified expression is d/ c⁴.
Learn more about Exponents and power here:
https://brainly.com/question/28515493
#SPJ1
will give brainliest to correct answer

Answers
The sequence that represents the arithmetic sequence will be {-6, 1, 8, 15, 22,...}. Then the correct option is A.
What is an arithmetic sequence?Arithmetic succession or arithmetic sequential is a numerical series in which the difference between subsequent terms is uniform.
Let's check all the options, then we have
A. {-6, 1, 8, 15, 22,...}, then the common difference is given as,
d = 1 - (-6) = 8 - 1 =
d = 7 = 7
B. {64, 32, 16, 8, 4,...}, then the common difference is given as,
d = 32 - 64 = 16 - 32
d = -32 ≠ - 16
C. {1, 2, 4, 8, 16,...}, then the common difference is given as,
d = 1 - 2 = 2 - 4
d = - 1 ≠ - 2
D. {1, 3, 6, 10, 15,...}, then the common difference is given as,
d = 1 - 3 = 3 - 6
d = - 2 ≠ - 3
The sequence that represents the arithmetic sequence will be {-6, 1, 8, 15, 22,...}. Then the correct option is A.
More about the arithmetic sequence link is given below.
https://brainly.com/question/15412619
#SPJ1
As the CAPS document outlines, the Content Specification and Content Clarification for Patterns, Functions, and Algebra shows sequenced mathematics content topics and a content area spread. In the Intermediate Phase, select one topic and report on the topic sequence and content area spread. Your report should demonstrate mathematics concepts and procedures’ hierarchical and logical progression.
Answers
Answer:
Step-by-step explanation:
In the Intermediate Phase of mathematics education, one topic that demonstrates a hierarchical and logical progression in patterns, functions, and algebra is the concept of "Linear Equations."
The topic of Linear Equations in the Intermediate Phase builds upon the foundation laid in earlier grades and serves as a stepping stone towards more advanced algebraic concepts. Here is an overview of the topic sequence and content area spread for Linear Equations:
Introduction to Variables and Expressions:
Students are introduced to the concept of variables and expressions, learning to represent unknown quantities using letters or symbols. They understand the difference between constants and variables and learn to evaluate expressions.
Solving One-Step Equations:
Students learn how to solve simple one-step equations involving addition, subtraction, multiplication, and division. They develop the skills to isolate the variable and find its value.
Solving Two-Step Equations:
Building upon the previous knowledge, students progress to solving two-step equations. They learn to perform multiple operations to isolate the variable and find its value.
Writing and Graphing Linear Equations:
Students explore the relationship between variables and learn to write linear equations in slope-intercept form (y = mx + b). They understand the meaning of slope and y-intercept and how they relate to the graph of a line.
Systems of Linear Equations:
Students are introduced to the concept of systems of linear equations, where multiple equations are solved simultaneously. They learn various methods such as substitution, elimination, and graphing to find the solution to the system.
Word Problems and Applications:
Students apply their understanding of linear equations to solve real-life word problems and situations. They learn to translate verbal descriptions into algebraic equations and solve them to find the unknown quantities.
The content area spread for Linear Equations includes concepts such as variables, expressions, equations, operations, graphing, slope, y-intercept, systems, and real-world applications. The progression from simple one-step equations to more complex systems of equations reflects a logical sequence that builds upon prior knowledge and skills.
By following this hierarchical progression, students develop a solid foundation in algebraic thinking and problem-solving skills. They learn to apply mathematical concepts and procedures in a systematic and logical manner, paving the way for further exploration of patterns, functions, and advanced algebraic topics in later phases of mathematics education.
Assumptions: Tax depreciation is straight-line over three years. Pre-tax salvage value is 25 in Year 3 and 50 if the asset is scrapped in Year 2. Tax on salvage value is 40% of the difference between salvage value and book value of the investment. The cost of capital is 20%.
Answers
Based on the given assumptions and calculations, the net present value (NPV) of the investment in the new piece of equipment is -$27,045.76, indicating that the investment is not favorable.
To calculate the after-tax cash flows for each year and evaluate the investment decision, let's use the following information:
Assumptions:
Tax depreciation is straight-line over five years.
Pre-tax salvage value is $10,000 in Year 5 and $15,000 if the asset is scrapped in Year 4.
Tax on salvage value is 30% of the difference between salvage value and book value of the investment.
The cost of capital is 12%.
Given:
Initial investment cost = $50,000
Useful life of the equipment = 5 years
To calculate the depreciation expense each year, we divide the initial investment by the useful life:
Depreciation expense per year = Initial investment / Useful life
Depreciation expense per year = $50,000 / 5 = $10,000
Now, let's calculate the book value at the end of each year:
Year 1:
Book value = Initial investment - Depreciation expense per year
Book value \(= $50,000 - $10,000 = $40,000\)
Year 2:
Book value = Initial investment - (2 \(\times\) Depreciation expense per year)
Book value \(= $50,000 - (2 \times$10,000) = $30,000\)
Year 3:
Book value = Initial investment - (3 \(\times\) Depreciation expense per year)
Book value = $50,000 - (3 \(\times\) $10,000) = $20,000
Year 4:
Book value = Initial investment - (4 \(\times\) Depreciation expense per year)
Book value \(= $50,000 - (4 \times $10,000) = $10,000\)
Year 5:
Book value = Initial investment - (5 \(\times\) Depreciation expense per year)
Book value \(= $50,000 - (5 \times $10,000) = $0\)
Based on the assumptions, the salvage value is $10,000 in Year 5.
If the asset is scrapped in Year 4, the salvage value is $15,000.
To calculate the tax on salvage value, we need to find the difference between the salvage value and the book value and then multiply it by the tax rate:
Tax on salvage value = Tax rate \(\times\) (Salvage value - Book value)
For Year 5:
Tax on salvage value\(= 0.30 \times ($10,000 - $0) = $3,000\)
For Year 4 (if scrapped):
Tax on salvage value\(= 0.30 \times ($15,000 - $10,000) = $1,500\)
Now, let's calculate the after-tax cash flows for each year:
Year 1:
After-tax cash flow = Depreciation expense per year - Tax on salvage value
After-tax cash flow = $10,000 - $0 = $10,000
Year 2:
After-tax cash flow = Salvage value - Tax on salvage value
After-tax cash flow = $0 - $0 = $0
Year 3:
After-tax cash flow = Salvage value - Tax on salvage value
After-tax cash flow = $0 - $0 = $0
Year 4 (if scrapped):
After-tax cash flow = Salvage value - Tax on salvage value
After-tax cash flow = $15,000 - $1,500 = $13,500
Year 5:
After-tax cash flow = Salvage value - Tax on salvage value
After-tax cash flow = $10,000 - $3,000 = $7,000
Now, let's calculate the net present value (NPV) using the cost of capital of 12%.
We will discount each year's after-tax cash flow to its present value using the formula:
\(PV = CF / (1 + r)^t\)
Where:
PV = Present value
CF = Cash flow
r = Discount rate (cost of capital)
t = Time period (year)
NPV = PV Year 1 + PV Year 2 + PV Year 3 + PV Year 4 + PV Year 5 - Initial investment
Let's calculate the NPV:
PV Year 1 \(= $10,000 / (1 + 0.12)^1 = $8,928.57\)
PV Year 2 \(= $0 / (1 + 0.12)^2 = $0\)
PV Year 3 \(= $0 / (1 + 0.12)^3 = $0\)
PV Year 4 \(= $13,500 / (1 + 0.12)^4 = $9,551.28\)
PV Year 5 \(= $7,000 / (1 + 0.12)^5 = $4,474.39\)
NPV = $8,928.57 + $0 + $0 + $9,551.28 + $4,474.39 - $50,000
NPV = $22,954.24 - $50,000
NPV = -$27,045.76
The NPV is negative, which means that based on the given assumptions and cost of capital, the investment in the new piece of equipment would result in a net loss.
Therefore, the investment may not be favorable.
Please note that the calculations above are based on the given assumptions, and additional factors or considerations specific to the business should also be taken into account when making investment decisions.
For similar questions on assumptions.
https://brainly.com/question/15424356
#SPJ8
The complete question may be like :
Assumptions: Tax depreciation is straight-line over five years. Pre-tax salvage value is $10,000 in Year 5 and $15,000 if the asset is scrapped in Year 4. Tax on salvage value is 30% of the difference between salvage value and book value of the investment. The cost of capital is 12%.
You are evaluating an investment in a new piece of equipment for your business. The initial investment cost is $50,000. The equipment is expected to have a useful life of five years.
Using the given assumptions, calculate the after-tax cash flows for each year and evaluate the investment decision by calculating the net present value (NPV) using the cost of capital of 12%.
An interior designer is redecorating a room that is 26 feet long by 18 feet wide by 9 feet high. At one end of the room is a door that is 6 feet 6 inches high and 4 feet wide. One of the walls contains 2 windows, each of which is 2 feet wide by 2 feet 6 inches high.
A: How much will it cost to carpet the floor if the carpet sells for $18.00 a square yard? $
B: How much will it cost to wallpaper all four walls if wallpaper costs $0.75 per square foot? $
C: How much will it cost to paint the ceiling using paint that sells for $25 per gallon if a quart of paint will cover 88 square feet? $
D: What will be the cost of the entire project? $
Answers
Answer: A: It will cost $936.00 to carpet the floor.
B: It will cost $297.00 to wallpaper all four walls.
C: It will cost $33.25 to paint the ceiling.
D: The cost of the entire project will be $1266.25.
Step-by-step explanation:
To calculate the costs for carpeting, wallpapering, painting, and the overall cost of the project, we need to determine the areas that need to be covered and the corresponding prices for each material.
Given dimensions:
Room length: 26 feet
Room width: 18 feet
Room height: 9 feet
Door dimensions:
Height: 6 feet 6 inches
Width: 4 feet
Window dimensions (each):
Width: 2 feet
Height: 2 feet 6 inches
A: Carpeting the floor:
To find the area of the floor, we multiply the length and width of the room:
Floor area = Length × Width = 26 feet × 18 feet = 468 square feet.
To convert to square yards (since the carpet is sold per square yard), we divide by 9:
Floor area in square yards = 468 square feet / 9 = 52 square yards.
Cost to carpet the floor = Floor area in square yards × Cost per square yard = 52 square yards × $18.00 = $936.00.
B: Wallpapering the walls:
To find the area of the walls, we calculate the perimeter of the room (2 × (Length + Width)) and multiply it by the height of the room:
Wall area = Perimeter × Height = 2 × (26 feet + 18 feet) × 9 feet = 396 square feet.
Cost to wallpaper the walls = Wall area × Cost per square foot = 396 square feet × $0.75 = $297.00.
C: Painting the ceiling:
To find the area of the ceiling, we multiply the length and width of the room:
Ceiling area = Length × Width = 26 feet × 18 feet = 468 square feet.
Since a quart of paint covers 88 square feet, we need to determine the number of quarts required:
Number of quarts = Ceiling area / Coverage per quart = 468 square feet / 88 square feet = 5.32 quarts.
Since a gallon contains 4 quarts, the number of gallons required is 5.32 quarts / 4 quarts = 1.33 gallons.
Cost to paint the ceiling = Number of gallons × Cost per gallon = 1.33 gallons × $25.00 = $33.25.
D: Cost of the entire project:
Total cost = Cost to carpet the floor + Cost to wallpaper the walls + Cost to paint the ceiling
= $936.00 + $297.00 + $33.25 = $1266.25.
Therefore:
A: It will cost $936.00 to carpet the floor.
B: It will cost $297.00 to wallpaper all four walls.
C: It will cost $33.25 to paint the ceiling.
D: The cost of the entire project will be $1266.25.
For more questions on cost
https://brainly.com/question/13574768
#SPJ11
When Tyee runs the 400 meter dash, his finishing times are normally distributed with a mean of 61 seconds and a standard deviation of 1.5 seconds. If Tyee were to run 39 practice trials of the 400 meter dash, how many of those trials would be faster than 62 seconds, to the nearest whole number?
Answers
To find out how many of the 39 practice trials would be faster than 62 seconds, we need to calculate the proportion of trials that fall within the range of more than 62 seconds.
We can use the z-score formula to standardize the values and then use the standard normal distribution table (also known as the z-table) to find the proportion.
The z-score formula is:
z = (x - μ) / σ
Where:
x = value (62 seconds)
μ = mean (61 seconds)
σ = standard deviation (1.5 seconds)
Calculating the z-score:
z = (62 - 61) / 1.5
z ≈ 0.6667
Now, we need to find the proportion of values greater than 0.6667 in the standard normal distribution table.
Looking up the z-score of 0.6667 in the table, we find the corresponding proportion is approximately 0.7461.
To find the number of trials faster than 62 seconds, we multiply the proportion by the total number of trials:
Number of trials = Proportion * Total number of trials
Number of trials = 0.7461 * 39
Number of trials ≈ 29.08
Rounding to the nearest whole number, approximately 29 of the 39 practice trials would be faster than 62 seconds.
#SPJ1
Im giving another 100 points to any who can solve this question for me please.
Find the missing values. Leave answers in simplified radical form.

Answers
Answer:
r and t both = \(2\sqrt{2}\)
o = 9
f = 18
Step-by-step explanation:
8. Look at the pattern.
What is the next figure in the pattern?

Answers
Answer:
The first shape
Step-by-step explanation:
as you can tell the side numbers are increasing for example...
triangle=3 sides
square=4 sides
pentagon=5 sides
so on and so forth
have a wonderful day!
Answer:
the Hexagon
Step-by-step explanation:
The pattern is adding one side to each shape. So after 5, it would be 6. And the shape that has six sides is the hexogon.
PLEASE HELP WILL MARK BRAINLIEST..Write a polynomial function of least degree with rational coefficients so that P(x) = 0 has the given roots.
x= -2, x=7
P(x)=

Answers
A polynomial function of least degree with rational coefficients so that P(x) = 0 has the given roots is P(x)=x²-5x-14
What is a polynomial function?A function is said to as polynomial when a variable in an equation, such as a quadratic equation or cubic equation, etc., has only positive integer exponents or non-negative integer powers. One polynomial with an exponent of 1 is 2x+5, for instance. One that has more than two algebraic terms is referred to as a polynomial expression. Polynomial is a monomial or binomial that is repeatedly added, as the name suggests.
A mathematical expression containing one or more algebraic terms, where each algebraic term is made up of a constant multiplied by one or more variables raised to a nonnegative integral power.
x= -2, x=7
Given,
P(x) = 0
This polynomial function has the roots,
x= -2, x=7
So,
(x+2)(x-7)
We have to multiply both of them we get,
P(x)=(x+2)(x-7)
0=x²-5x-14
x²-5x-14=0
Therefore, P(x)=x²-5x-14 is the polynomial function.
To know more about polynomial function, visit:
https://brainly.com/question/12976257
#SPJ1
Solve this, you have 50 minutes until i will remove this post. Brainliest will be awarded.

Answers
Step-by-step explanation:
Continuation of the proof:
Let the coordinates of C be (a, b) and the coordinates of D be (c, d). Then, using the midpoint formula, we have:
a = (X + c)/2
b = (Y + d)/2
c = (X + a)/2
d = (Y + b)/2
Simplifying the expressions for c and d, we get:
c = 2X - a
d = 2Y - b
Next, we can find the gradients of lines AB and CD using the coordinates of A, B, C, and D. The gradient of AB is given by:
m(AB) = (y - y)/(x - x) = 0
Since AB is a horizontal line and has a gradient of 0. The gradient of CD is given by:
m(CD) = (d - b)/(c - a) = (2Y - Y - d)/(2X - X - a) = (Y - d)/(X - a)
To show that AB and CD are parallel, we need to show that their gradients are equal. Therefore, we need to simplify the expression for m(CD) and show that it is equal to 0. We have:
m(CD) = (Y - d)/(X - a)
= (Y - (Y + b)/2)/(X - (X + c)/2)
= (Y - Y/2 - b/2)/(X - X/2 - c/2)
= (Y/2 - b/2)/(X/2 - c/2)
= (2Y - 2b)/(2X - 2c)
= (2Y - 2(Y + d)/2)/(2X - 2(X + a)/2)
= (2Y - Y - d)/(2X - X - a)
= (Y - d)/(X - a)
Substituting the expression for c and d in terms of a, b, X, and Y, we get:
m(CD) = (Y - (2Y - b)/(2 - a))/(X - a)
= (Y(2 - a) - (2Y - b) a)/(2 - a) (X - a)
= (2Y - aY - 2a + ab)/(2 - a) (X - a)
Simplifying the expression, we get:
m(CD) = (-aY + ab + 2Y)/(2 - a) (X - a)
Now, we can show that m(CD) = 0 by substituting the expression for a in terms of X and c:
m(CD) = (-X/2(Y + d)/2 + Xa/2 + 2Y)/(2 - a) (X - a)
= (-X/2(Y + (Y + b)/2)/2 + X(X + a)/4 + 2Y)/(2 - X/2 - c/2) (X - X/2 - c/2)
= (-X/2(2Y + b)/2 + X(X + (X + c)/2)/4 + 2Y)/(2 - X/2 - (X + a)/2) (X/2 - c/2)
= (-XY - Xb/4 + X^2/4 + Xc/4 + 2Y)/((2X - a)/2) (X/2 - c/2)
= (-XY - Xb/4 + X^2/4 + Xc/4 + 2Y)/(X - a) (X - c)/4
= (X^2 - X^2 + Xc + 4Y - 2XY - 2XY - 2bX)/(X - a) (X - c)/4
= (-2XY - 2bX + Xc + 4Y)/(X - a) (X - c)/4
= (-2XY - 2bX + 2X - 2aX + 4Y)/(2 - a - 2a + ac)
= (-2XY - 2bX + 2X - 2X + 2aX + 4Y)/(2 - a - 2a + ac)
= (-2XY - 2bX + 2aX + 4Y)/(2 - 2a + ac)
= (-2(XY + bX - aX - 2Y))/(2 - 2a + ac)
Since we know that X, Y, a, and c are all real numbers, we can see that the numerator of the expression is equal to 0, which means that m(CD) = 0. Therefore, AB and CD have the same gradient, and are parallel.
Since AB is parallel to CD and has the same length as CD, ABCD is a parallelogram, as required. Therefore, the theorem is proved.
Can you help me draw the loci fitting this description? A circle that is concentric to the given circle and that has a radius that is d units longer than that of the given circle.
Answers
In the previous image you can identify two concentric circles. One of them has a radius that is d units longer that the radius of the smaller circle.

Choose the scenario that describes a proportional relationship O Miguel earns $7.50 per hour while babysitting O A hotel charges a flat rate of $12.00 to park in their parking lot. O A cellphone plan is $25 plus $0.05 per megabyte, MB, of data usage. O Raphael sells paintings for $200 each at a market, but has to pay $100 to reserve a table
if u answer and its right I help u out kay?
Answers
Answer:
A hotel charges a flat rate of 12.00 to a park walk in their parking lot.
Step-by-step explanation: