A triangle drawn on a map has sides that measure 7 cm, 14 cm, and 12 cm. the shortest of the corresponding real-life distances is 120 km. find the longest of the real-life distances.
Answers
The longest real-life distance is approximately 205.71 km.
To find the longest real-life distance, we need to determine which side of the triangle corresponds to the longest real-life distance.
Given that the shortest real-life distance is 120 km, we can use this information to set up a proportion between the lengths on the map and the real-life distances.
Let's assume that the longest side of the triangle corresponds to the longest real-life distance, which we'll call "x" km.
Using the proportion:
7 cm / 120 km = 12 cm / x km
We can cross multiply and solve for x:
7x = 120 * 12
7x = 1440
x = 1440 / 7
x ≈ 205.71 km
Therefore, the longest real-life distance is approximately 205.71 km.
Know more about longest real-life distance here:
https://brainly.com/question/31136574
#SPJ11
Related Questions
what does the highest point on a bell-shaped curve represent?
Answers
The highest point on a bell-shaped curve represents the peak or maximum value of the distribution. This point is known as the mode of the distribution.
In a bell-shaped curve, also known as a normal distribution or Gaussian distribution, the data is symmetrically distributed around the mean. The curve is characterized by a central peak, and the highest point on this peak corresponds to the mode.
The mode represents the most frequently occurring value or the value that has the highest frequency in the dataset. It is the point of highest density in the distribution.
The bell-shaped curve is often used to model naturally occurring phenomena and is widely applied in statistics and probability theory. The mode provides information about the most common or typical value in the dataset and is useful for understanding the central tendency of the distribution.
While the mean and median also have significance in a normal distribution, the highest point on the bell-shaped curve specifically represents the mode, indicating the value with the highest occurrence in the dataset.
Learn more about Gaussian distribution at: brainly.com/question/29734279
#SPJ11
find the distance between the points (3, 7) and (2, 6)
Answers
Answer:
1.414214
Step-by-step explanation:
I think this is right lol.
6x + 5y = 4 5. and 6x – 7y = –20 what does x and y equal?
Answers
Answer:
x=-1 y=2
Step-by-step explanation:
Use Elimination or Substitution (Elimination shown below)
6x+5y=4
6x-7y =-20 <- Multiply by -1
-6x+7y=20
12y = 24
y=2
Plug back into either of the equations and solve for x.
6x + 10= 4
6x = -6
x = -1
Double check work:
-6+10 = 4
a total of 35% of americans smoke cigarettes, 15% smoke cigars and 7% smoke both cigarettes and cigars. a. what percentage smoke something (cigars, cigarettes or both)? b. what percentage smoke neither cigars nor cigarettes? c. what percentage smoke cigars but not cigarettes? d. what is the conditional probability that a randomly selected person smokes cigarettes given that he smokes cigars? g
Answers
The solution of each part of the question is given below:
a. Let C be the event that a person smokes cigars, and let S be the event that a person smokes cigarettes. The percentage of Americans who smoke either cigars, cigarettes, or both can be calculated as P(C U S), where U represents the union of two events. From the given information, P(C) = 15% and P(S) = 35%. The probability that a person smokes both cigars and cigarettes is 7%, so P(C ∩ S) = 7%.
P(C U S) = P(C) + P(S) - P(C ∩ S)
P(C U S) = 15% + 35% - 7% = 43%
So, 43% of Americans smoke either cigars, cigarettes, or both.
b. The percentage of Americans who smoke neither cigars nor cigarettes can be calculated as P(C' ∩ S'), where C' represents the complement of event C (not smoking cigars) and S' represents the complement of event S (not smoking cigarettes).
P(C' ∩ S') = 100% - P(C U S)
P(C' ∩ S') = 100% - 43% = 57%
So, 57% of Americans smoke neither cigars nor cigarettes.
c. The percentage of Americans who smoke cigars but not cigarettes can be calculated as P(C ∩ S').
P(C ∩ S') = P(C) - P(C ∩ S)
P(C ∩ S') = 15% - 7% = 8%
So, 8% of Americans smoke cigars but not cigarettes.
d. The conditional probability that a person smokes cigarettes given that he smokes cigars can be calculated as P(S | C), where S represents the event that a person smokes cigarettes and C represents the event that a person smokes cigars.
P(S | C) = P(S ∩ C) / P(C)
P(S | C) = 7% / 15% = 0.47
So, the conditional probability that a randomly selected person smokes cigarettes given that he smokes cigars is 0.47, or 47%.
You can learn more about conditional probability at
https://brainly.com/question/23382435
#SPJ4
Subtract 4x + 2y - 16z from ( -12x + 2y - 4z ).
Answers
Answer:
Step-by-step explanation:
4x + 2y - 16z - (-12x + 2y - 4z)
4x + 2y - 16z + 12x - 2y + 4z
16x - 12z
show that a limit of a convergent sequence of complex numbers is unique by appealing to the corresponding result for a sequence of real numbers.
Answers
The limit of a convergent sequence of complex numbers is unique.
To show that the limit of a convergent sequence of complex numbers is unique by appealing to the corresponding result for a sequence of real numbers,
we use the fact that a sequence of complex numbers can be represented as a sequence of ordered pairs of real numbers.
Let {z_n} be a sequence of complex numbers with two distinct limits, say a and b.
Then we can writez_n = (x_n, y_n) where x_n and y_n are the real and imaginary parts of z_n, respectively.
Since {z_n} converges to a,
we have both x_n -> Re(a) and y_n -> Im(a) as n -> infinity.
Similarly, since {z_n} converges to b,
we have both x_n -> Re(b) and y_n -> Im(b) as n -> infinity.
Using the corresponding result for a sequence of real numbers,
we can conclude that {x_n} converges to Re(a) and to Re(b), while {y_n} converges to Im(a) and to Im(b).
However, the limit of a product of two sequences is the product of their limits if both limits exist.
Therefore, we havez_n = (x_n, y_n) -> (Re(a), Im(a)) andz_n = (x_n, y_n) -> (Re(b), Im(b))as n -> infinity, which implies that (Re(a), Im(a)) = (Re(b), Im(b)).
Hence, a = b, and the limit of a convergent sequence of complex numbers is unique.
To know more about complex numbers,visit:
https://brainly.com/question/20566728
#SPJ11
Solve the differential equation by variation of parameters.
y'' − y = cosh x
Answers
The general solution is \($$y=c_3 e^x+c_4 e^{-x}+\frac{1}{2} x \sinh x \text {. }$$\)
Consider the following differential equation: y'' − y = cosh x
The given differential equation in the operator form will be: (D^2-1)y=coshx
The auxiliary equation of the corresponding homogeneous equation will be:
m^2-1 = 0
=>m^2=1
=>m=+1,-1
So, the complementary function will be \(y_c=c_1 e^x+c_2 e^{-x}.\alpha\)
Now, let \(y_1=e^x, y_2=e^{-x}.\)
Compute the Wronskian determinant:
\($$\begin{aligned}W\left(y_1, y_2\right) & =\left|\begin{array}{ll}y_1 & y_2 \\y_1^{\prime} & y_2^{\prime}\end{array}\right| \\& =\left|\begin{array}{ll}e^x & e^{-x} \\e^x & -e^{-x}\end{array}\right| \\& =-e^x e^{-x}-e^x e^{-x} \\& =-2\end{aligned}$$\)
Since the given differential equation is already in the form \($y^{\prime \prime}+P(x) y^{\prime}+Q(x) y=f(x)$\) (that is, the coefficient of y'' is 1 ),
So identify:
f(x)=cosh x
Then, calculate the values of u_1' and u_2', using formulas as follows:
\($$\begin{aligned}u_1^{\prime} & =-\frac{y_2 f(x)}{W} & u_2^{\prime} & =\frac{y_1 f(x)}{W} \\& =-\frac{e^{-x} \cdot \cosh x}{-2} & & =\frac{e^x \cdot \cosh x}{-2} \\& =\frac{e^{-x} \cdot\left(\frac{e^x+e^{-x}}{2}\right)}{2} & \text { and } & =-\frac{e^x \cdot\left(\frac{e^x+e^{-x}}{2}\right)}{2} \\& =\frac{1}{4}\left(1+e^{-2 x}\right) & & =-\frac{1}{4}\left(e^{2 x}+1\right)\end{aligned}$$\)
Integrate on both sides of u_1' and u_2' with respect to ' x', to get:
\($$u_1=\frac{x}{4}-\frac{e^{-2 x}}{8} \text { and } u_2=-\frac{x}{4}-\frac{e^{2 x}}{8} .$$\)
So, the particular solution is,
\($$\begin{aligned}y_p & =u_1 y_1+u_2 y_2 \\& =\left(\frac{x}{4}-\frac{e^{-2 x}}{8}\right) e^x+\left(-\frac{x}{4}-\frac{e^{2 x}}{8}\right) e^{-x} \\& =\frac{1}{4} x\left(e^x-e^{-x}\right)-\frac{1}{8}\left(e^{-x}+e^x\right) \\& =\frac{1}{2} x \sinh x-\frac{1}{8}\left(e^{-x}+e^x\right)\end{aligned}$$\)
Thus, the general solution of the given differential equation is,
\($$\begin{aligned}y & =y_c+y_p \\& =c_1 e^x+c_2 e^{-x}+\frac{1}{2} x \sinh x-\frac{1}{8} e^{-x}-\frac{1}{8} e^x \\& =\left(c_1-\frac{1}{8}\right) e^x+\left(c_2-\frac{1}{8}\right) e^{-x}+\frac{1}{2} x \sinh x \\& =c_3 e^x+c_4 e^{-x}+\frac{1}{2} x \sinh x\end{aligned}$$\)
For more questions on Differential Equation
https://brainly.com/question/19130837
#SPJ4
Solve for x plz and thank you smmmm

Answers
Answer:
12x-4=80
12x=80+4
=84
x=84÷12
=7
x^2 + 5x + 6
enter your next step here:
Answers
then you can turn this into (x+2)(x+3)
What is the missing side length in this right triangle? Round the answer to the nearest tenth.
A: 4.7 units
B: 6.6 units
C: 15.6 units

Answers
Answer:
The answer is B. i.e. 6.6units.
i might give the crown

Answers
Answer:
Area=88in squared
Step-by-step explanation:
Answer 128 to the second power
explanation:
its 128 to the second power because if you multiply 16*8 and you will get 128to the second power
URGENT!!!!! LAST QUESTIONS!!!!!!! WILL GIVE BRANLIEST!!!AT LEAST TAKE A LOOK!!!!!! PLS HELP!!!URGENT!!!!!
16. Which piece of information below will not help you prove that triangles ABC and DEF are congruent using ASA?
IF YOU REALLY LOOK YOU CAN SEE THE LETTERS BUT IN CASE HERE:
PIC BELOW ON THE LEFT TRIANGLE: A IS ON THE BOTTOM LEFT. B IS AT THE TOP, POINTY PART, C IS ON THE BOTTOM RIGHT
ON THE RIGHT TRIANGLE: D IS ON THE BOTTOM LEFT. E IS AT THE TOP, POINTY PART, F IS ON THE BOTTOM RIGHT
A) AC=DF
B) AB=DE
C) B=E
D) A=D

Answers
Answer: A) AC=DF
Step-by-step explanation:
Angle-Side-Angle (ASA) Postulate: If 2 angles and the included side of one triangle are congruent to 2 angles and the included side of another triangle, then the triangles are congruent.
Answer A is the only one that wouldn’t help you prove that these triangles are congruent.
Answer this question plz

Answers
The measure of angle EDF from the given figure is 23°.
From the given figure, ∠EGF=23°.
What is and angles in the same segment theorem?The angles at the circumference subtended by the same arc are equal. More simply, angles in the same segment are equal.
By using angles in the same segment theorem, we get
∠EGF = ∠EDF = 23°
Therefore, the measure of angle EDF from the given figure is 23°.
To learn more about the circle theorems visit:
https://brainly.com/question/19906313.
#SPJ2
Plz help it’s due tonight!!!

Answers
Explanation: Since the original SVP ≈ MTQ statement is ordered from which angles are equivalent to each other, I assumed that Q ≈ P and M ≈ S, which is why PS ≈ QM might be the answer.
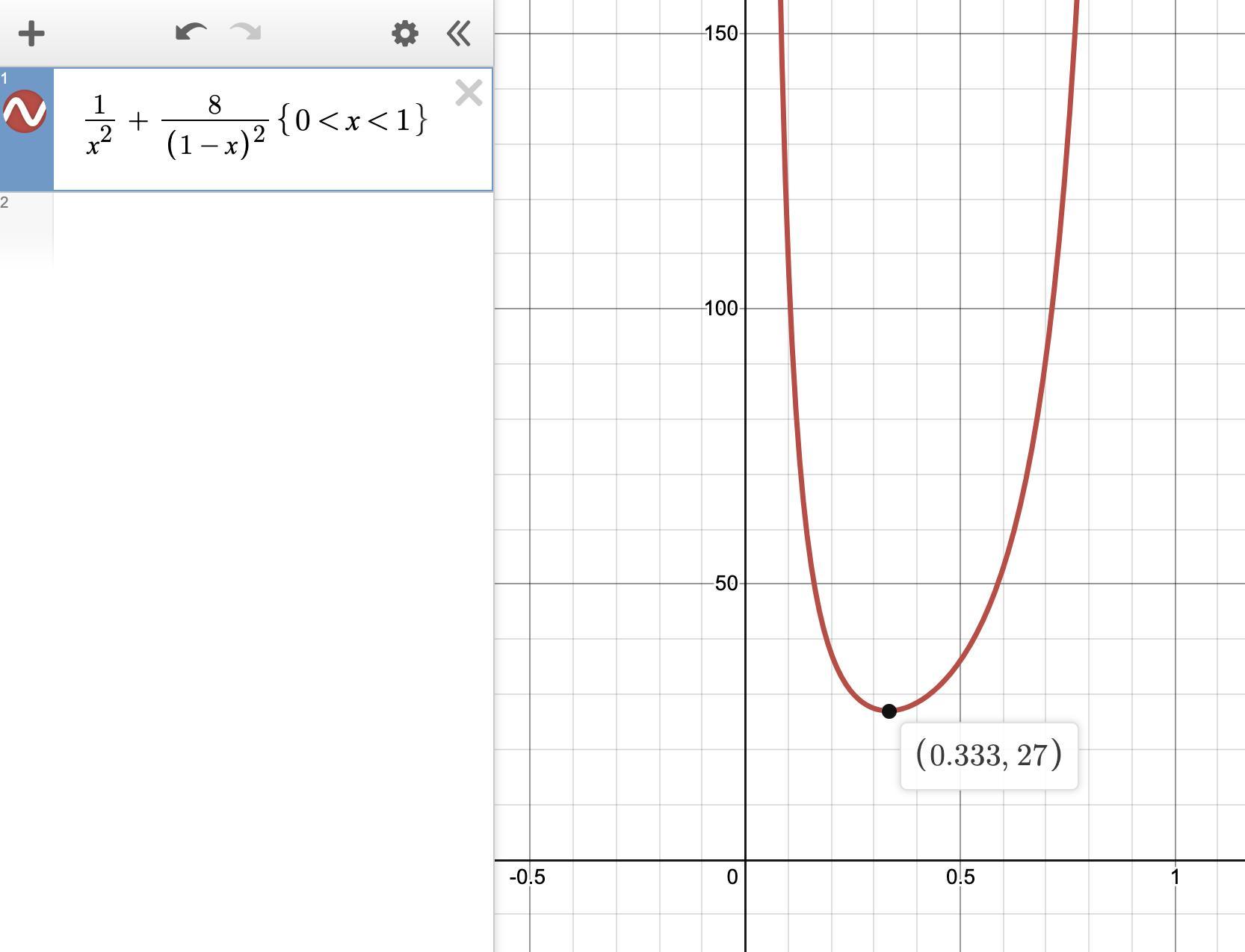
A smokestack deposits soot on the ground with a concentration inversely proportional to the square of the distance from the stack. With two smokestacks d miles apart, the concentration of the combined deposits on the line joining them, at a distance x from one stack, is given by:
\(S=\frac{c}{x^2} +\frac{k}{(d-x)^2}\)
where c and k are positive constants which depend on the quantity of smoke each stack is emitting. If k=8c, find the point on the line joining the stacks where the concentration of the deposit is a minimum. xmin= ? miles
Answers
Answer:
d/3
Step-by-step explanation:
For k = 8c, the concentration is ...
S = c/x^2 + 8c/(d -x)^2
The minimum of the function will be found where its derivative is zero. The derivative with respect to x is ...
S' = -2c/x^3 +(-2)(8c)(-x)/(d -x)^3
We are interested in the value of x that makes this zero.
0 = -2c/x^3 +16c/(d -x)^3 . . . . . simplify slightly, set S'=0
0 = (-2(d -x)^3 +16x^3)/(x(d -x))^3 . . . . . combine terms, divide by c
0 = d^3 -3d^2x +3dx^2 -x^3 -8x^3 . . . . multiply by (x(d-x))^3/(-2)
9x^3 -3dx^2 +3d^2x -d^3 = 0 . . . . . simplified cubic
Factoring by grouping, we have ...
(9x^3 -3dx^2) +(3d^2x -d^3) = 0
3x^2(3x -d) +d^2(3x -d) = 0
(3x^2 +d^2)(3x -d) = 0
The solution will be found where the second of these factors is zero:
3x -d = 0
x = d/3
The concentration of the deposit is a minimum at x = d/3 miles.
_____
The graph shows the minimum is x = 1/3 when d = 1.
Write an equation in slope-intercept form for the line that has the given slope and
contains the point. m=3;(-1,-2)
Answers
Answer:
P(1,2) m = 3 Since you are given a point and a slope, use the point-slope form for the equation of a line: y - y1 = m(x - x1)
y - 2 = 3(x - 1)
y - 2 = 3x - 3
y = 3x - 1 hope this helps
Step-by-step explanation:
Answer
y=3x+1
put in point slope form y-yone=m(x-x one)
y+2=3(x+1)
y+2=3x+3
y=3x+1
find the general solution of the given higher-order differential equation. d 4y dx4 − 2 d 2y dx2 − 8y = 0
Answers
he required solution is \(y=c_1e^{2x}+c_2e^{-2x}+c_3\sqrt2\cos(\sqrt2x)+c_4\sqrt2\sin(\sqrt2x)\)
where \(c_1,c_2,c_3\) and \(c_4\) are constants.
Let’s assume the general solution of the given differential equation is,
y=e^{mx}
By taking the derivative of this equation, we get
\(\frac{dy}{dx} = me^{mx}\\\frac{d^2y}{dx^2} = m^2e^{mx}\\\frac{d^3y}{dx^3} = m^3e^{mx}\\\frac{d^4y}{dx^4} = m^4e^{mx}\\\)
Now substitute these values in the given differential equation.
\(\frac{d^4y}{dx^4}-2\frac{d^2y}{dx^2}-8y\\=0m^4e^{mx}-2m^2e^{mx}-8e^{mx}\\=0e^{mx}(m^4-2m^2-8)=0\)
Therefore, \(m^4-2m^2-8=0\)
\((m^2-4)(m^2+2)=0\)
Therefore, the roots are, \(m = ±\sqrt{2} and m=±2\)
By applying the formula for the general solution of a differential equation, we get
General solution is, \(y=c_1e^{2x}+c_2e^{-2x}+c_3\sqrt2\cos(\sqrt2x)+c_4\sqrt2\sin(\sqrt2x)\)
Hence, the required solution is \(y=c_1e^{2x}+c_2e^{-2x}+c_3\sqrt2\cos(\sqrt2x)+c_4\sqrt2\sin(\sqrt2x)\)
where \(c_1,c_2,c_3\) and \(c_4\) are constants.
Know more about constants here:
https://brainly.com/question/27983400
#SPJ11
The double-reciprocal transformation of the Michaelis-Menten equation, also called the Lineweaver- Burk plot, is given by
1/V_0 = K_m /(V_max[S]) + 1/V_max
To determine Km from a double-reciprocal plot, you would:
A) multiply the reciprocal of the x-axis intercept by -1.
B) multiply the reciprocal of the y-axis intercept by -1.
C) take the reciprocal of the x-axis intercept.
D) take the reciprocal of the y-axis intercept.
E) take the x-axis intercept, where V_0 = 1/2 V_max.
Answers
To determine Km from a double-reciprocal plot, you would choose option (A) which is to multiply the reciprocal of the x-axis intercept by -1.
In the double-reciprocal plot equation, the x-axis intercept is -1/Km, and the y-axis intercept is 1/Vmax. Therefore, if you take the reciprocal of the x-axis intercept, you get -Km, and multiplying it by -1 gives you Km.
This method is preferred because it is more accurate than estimating Km based on the position of the curve on the plot or by taking the x-axis intercept where V0 = 1/2 Vmax, which can be influenced by experimental error.
To learn more about reciprocal here:
https://brainly.com/question/30519664
#SPJ4
Alex painted 178 ft2 of his apartment’s walls with 13 1 3 gallon of paint. He has 2 gallons of paint in all. If he wants to cover 1,000 ft2 of his apartment, does he have enough paint? Complete a true statement
Answers
From multiplcation operation, Alex has enough paint to cover 1,000 ft² of his apartment. The true statement is 2 gallons of paint will cover 1068 ft², Alex have enough paint of quantity 2 gallons.
We have Mr. Alex painted his apartment. Area of his apartment'walls = 178 ft²
Quantity of paint used by him to paint his apartment'walls with area 178 ft² =\( \frac{1}{3} \: \: gallons\)
Total quantity of paint used in all
= 2 gallons
We have to check the provide paint is enough or not to cover 1,000 ft² of his apartment. Let the required paint for 1000 ft² be x gallons. Using multiplcation, 1/3 gallons quantity of paint will cover the area of apartment = 178 ft², so, 1 gallons quantity of paint will cover the area of apartment = 178 ×3 ft²= 534 ft²
Now, 2 gallons quantity of paint will cover the area of apartment = 2× 534 ft² = 1068 ft²> 1000 ft²
But he wants to paint 1000 ft² of his apartment in 2 gallons quantity (x=1.9 gal ). So, he has enough paint to paint his apartment.
For more information about multiplcation, visit:
https://brainly.com/question/28773316
#SPJ4
Complete question:
The above figure complete the question.
Alex painted 178 ft2 of his apartment’s walls with 1/3 gallon of paint. He has 2 gallons of paint in all. If he wants to cover 1,000 ft2 of his apartment, does he have enough paint? Complete a true statement

A survey was carried out among 120 school children looked at which type of meat they preferred. 55%said they preferred lamb,20% said they preferred chicken, 15% preferred duck and 10% turkey . calculate the number of children in each category
Answers
No. of children in lamb, chicken, duck, and turkey category is 66, 24, 18 and 12 respectively.
What is percentage ?Percentage is the value per hundredth.
According to the given question a survey was carried out among 120 school children looked at which type of meat they preferred. 55% said they preferred lamb,20% said they preferred chicken, 15% preferred duck and 10% turkey and we have to calculate no. of children in each category.
55% said they preferred lamb, So the no. of students i this category is
= (55/100)×120
= 66 children.
20% said they preferred chicken, So the no. of children in this category is
= (20/100)×120
= 24 children.
15% said they preferred duck, So the no. of children in this category is
= (15/100)×120
= 18 children.
10% said they preferred turkey, So the no. of children in this category is
= (10/100)×120
= 12 children.
learn more about percentage here :
https://brainly.com/question/19670755
#SPJ4
Write the equation of the line that passes through the points (-5, 9) and (8,-9).
Put your answer in fully simplified point-slope form, unless it is a vertical or
horizontal line.
Answers
Answer:
y - 9 = -18/13(x + 5)
Step-by-step explanation:
A pole that is 3.2 m tall casts a shadow that is 1.32 m long. At the same , a nearby tower casts a shadow that is 46.75 m long. How tall is the tower? Round your answer to the nearest meter.
Answers
Answer:
The tower is 113 meters.
Step-by-step explanation:
We are given a pole and a tower that both create a shadow.
Hence, the figures made are triangles.
If you draw the figure (attached to this response), you can see the two triangles are similar triangles.
⭐What are similar triangles?
two triangles whose corresponding side lengths are proportional and have the same shapeStrategycreate a proportion of the ratios of the corresponding side lengthssolve for the length of the towerCreate a ratio for the corresponding side lengthsThe length of the height of the pole (3.2) corresponds to the length of the height of the tower (x).
The length of the shadow of the pole (1.32) corresponds to the length of the shadow of the tower (46.75).
Therefore, our two ratios are:
\(\frac{3.2}{x}\) and \(\frac{1.32}{46.75}\)
Create a proportion for the corresponding side lengthsA proportion is when you set two ratios equal to each other:
\(\frac{3.2}{x} = \frac{1.32}{46.75}\)
Solve for the length of the tower (x)To solve for x, cross multiply by multiplying the opposite parts of the fraction together.
\(\frac{3.2}{x} = \frac{1.32}{46.75}\\46.75(3.2) = 1.32x\\149.6 = 1.32x\\\\113 = x\)
∴ The tower is 113 meters tall!
if this response helped you, please mark it the "brainliest" :)
solve this inequality 4.2x+5.6<7.2-8.3x
Answers

Find the product of (3x − 4)(2x2 + 2x − 1).
a
6x3 + 2x2 − 5x + 4
b
6x3 + 14x2 − 11x + 4
c
6x3 − 14x2 − 5x + 4
d
6x3 − 2x2 − 11x + 4
Answers
Answer:
Answer is D.)
6x3 - 2x2 - 11x + 4
decide if the statement is true or false. (a) the shape of a sampling distribution of sample means that follows the requirements of the central limit theorem will be approximately bell-shaped.
(b) A sampling distribution of sample means has a mean, μ /√n 1to
Answers
The statement ''the shape of a sampling distribution of sample means that follows the requirements of the central limit theorem will be approximately bell-shaped.'' is true. The statement ''A sampling distribution of sample means has a mean, μ /√n 1to.'' is false.
(a) According to the central limit theorem, when the sample size is sufficiently large, the sampling distribution of sample means will approximate a bell-shaped distribution, regardless of the shape of the population from which the samples are drawn. This is one of the key properties of the central limit theorem.
(b) The correct formula for the mean of a sampling distribution of sample means is μ, not μ/√n. The mean of the sampling distribution of sample means is equal to the population mean (μ). The formula μ/√n is used to calculate the standard deviation (σ) of the sampling distribution, not the mean.
To know more about sampling distribution refer here:
https://brainly.com/question/31465269#
#SPJ11
A chocolate chip cookies recipe calls for 4 and 1/4 cups of chocolate chips to make 10 dozen cookies Based on this recipe, how many cups of chocolate are needed to make 25 dozen cookies?
Answers
Answer:
The answer is 10 5/8
Step-by-step explanation:
Answer:
10 and5/8 cups
Step-by-step explanation:
4 and 4/1 cups for 10x12 cookies
17/4 cups for 120 cookies
34/8 cups for 120 cookies
17/8 cups for 60 cookies
we need to find 25 x 12 cookies = 300 = 120+120+60
17/8 + 34/8 +34/8 =85/8 =10and 5/8 cups
The density of copper is 8.94 g/cm^3. What is the mass of a rectangular sheet of copper: 10 cm wide, 45 cm long, and 0.2 cm thick?
Answers
Let mass=x
8.94= x/(10*45*.2)
X=8.94*90
Mass=804.6 g
Hope this helped :)
ANSWER ASAP!! TY :)
Lyme disease is an infection caused by bacteria. A test for Lyme disease may be affected by other medications and medical conditions. The testing results are summarized in the table.
Tested positive Tested negative Row Totals
Has Lyme disease 53% 17% 70%
Does not have Lyme disease 12% 18% 30%
Column Totals 65% 35% 100%
What percentage of all patients who took the test had a false positive result?
12%
17%
18%
35%
Answers
The percentage of all patients who took the test and had a false positive result will be 35%. Then the correct option is D.
What is the percentage?The amount of any product is given as though it was a proportion of a hundred. The ratio can be expressed as a quarter of 100. The phrase % translates to one hundred percent. It is symbolized by the character '%'.
Lyme illness is a disease brought about by microscopic organisms. A test for Lyme infection might be impacted by different prescriptions and ailments. The testing results are summed up in the table.
Tested positive Tested negative Row Totals
Has Lyme disease 53% 17% 70%
Doesnt have Lyme disease 12% 18% 30%
Column Totals 65% 35% 100%
The level of all patients who stepped through the examination and had a misleading positive outcome will be 35%. Then, at that point, the right choice is D.
More about the percentage link is given below.
https://brainly.com/question/8011401
#SPJ1
slope of (-5,1) and (0,9)
Answers
Answer:
8/5
Step-by-step explanation:
When we have two points , we can use the slope formula
m = ( y2-y1)/ ( x2-x1)
= ( 9-1)/(0--5)
(9-1)/(0+5)
8/5
Answer:
The answer is
\( \frac{8}{5} \\ \)Step-by-step explanation:
The slope of a line given two points can be found by using the formula
\(m = \frac{ y_2 - y _ 1}{x_ 2 - x_ 1} \\ \)
where
(x1 , y1) and (x2 , y2) are the points
From the question the points are
(-5,1) and (0,9)
The slope is
\(m = \frac{9 - 1}{0 + 5} = \frac{8}{5} \\ \)
We have the final answer as
\( \frac{8}{5} \\ \)
Hope this helps you
The numbers of trading cards owned by 7 middle-school students are given below.
(Note that these are already ordered from least to greatest.)
360, 386, 483, 526, 527, 560, 791
Suppose that the number 791 from this list changes to 574. Answer the following.
(a) What happens to the mean?
(b) What happens to the median?
○ It decreases by
O It increases by
O It stays the same.
O It decreases by
O It increases by
O It stays the same.
Answers
By answering the presented question, we may conclude that As a result, the median remains unchanged.
What is mean?The mean of a dataset is the sum of all values divided by the total number of values; this is also known as the arithmetic mean (as opposed to the geometric mean). This is the most often used measure of central tendency, sometimes known as the "mean." Merely dividing the entire number of values in the dataset by the sum of those values provides this result. Calculations may be performed using both raw data and data that has been compiled into frequency tables. The average of a number is referred to as its average. It is simple to calculate: Divide the total number of digits by the number of digits. the sum divided by the count.
(a) To get the mean of the original data set, add all of the values and divide by the total number of values:
Mean = (360 + 386 + 483 + 526 + 527 + 560 + 791) / 7 = 514
When we alter the value of 791 to 574, the new total is:
360 + 386 + 483 + 526 + 527 + 560 + 574 = 3416
As a result, the new mean is:
Mean = 3416 / 7 = 488
As a result, the mean falls by 26.
(b)
If we change 791 to 574, the resulting data set is as follows:
360, 386, 483, 526, 527, 560, 574
As we sort this data set from least to greatest, the median remains the fourth number (526).
As a result, the median remains unchanged.
To know more about mean visit:
https://brainly.com/question/30094057
#SPJ1