A U.S. Coast Guard Response Boat leaves Charleston, South Carolina at 1:30 p.m. heading due east at an average speed of 20 knots (nautical miles per hour). At 4:30 p.m., the boat changes course to N 18°18°E. At 8:00 p.m. what is the boat's bearing and distance from Charleston, South Carolina? Round all units to the nearest hundredth.
Bearing from Charleston, South Carolina:
Distance from Charleston, South Carolina:
Answers
Answer:
bearing: 50.8°distance: 105.3 nmiStep-by-step explanation:
You want the bearing and distance from Charleston, SC, of a boat after it travels at 20 knots from Charleston from 1:30 pm to 4:30 pm due east, then N 18° E until 8:00 pm.
Sum of vectorsIt is helpful if you are familiar with determining hours from clock times, and with the relation between time, speed, and distance. The first leg lasted 3 hours from 1:30 to 4:30. In that time, the boat traveled (20 nmi/h)·(3 h) = 60 nmi. The second leg lasted 3.5 hours from 4:30 to 8:00, so the distance traveled was (20 nmi/h)·(3.5 h) = 70 nmi.
There are several ways you can find the sum of the vectors representing the distance and bearing.
Geometry appThe first attachment shows the solution offered by a geometry app.
The boat is on a bearing of 50.8° from Charleston, at a distance of 105.3 nautical miles.
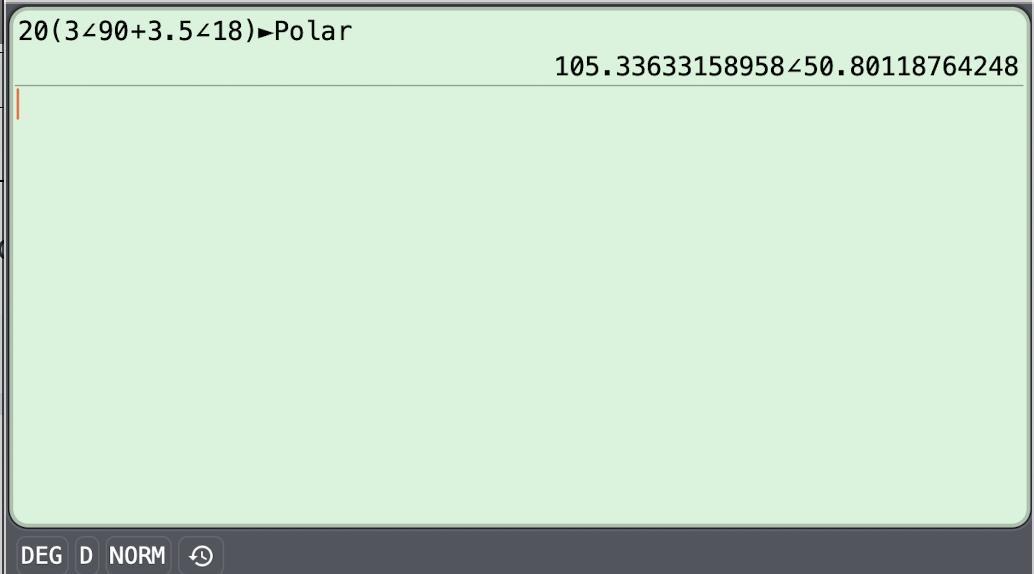
Vector calculatorThe second attachment shows the result of using a calculator to find the vector sum. For this, we factored out the speed and used hours for the magnitude of the vectors.
The boat is 105.3 nautical miles on a bearing of 50.8° from Charleston.
Law of cosinesYou can also find the magnitude of the distance using the law of cosines. The angle between the directions of travel is 90+18 = 108°, so the distance will be ...
c² = a² +b² -2ab·cos(C)
c² = 60² +70² -2·60·70·cos(108°) = 11095.74
c = √11095.74 = 105.3 . . . . nautical miles
The bearing north of east can now be found using the law of sines:
α = arcsin(sin(108°)·70/105.3) ≈ 39.2°
The bearing clockwise from north is then 90° -39.2° = 50.8°.
X-Y Coordinates60 nmi due east puts the boat at (60, 0) on an x-y plane. Traveling 70 nmi on a bearing 62° counterclockwise from east adds 70(cos(72°), sin(72°)) ≈ (21.63, 66.57) to the coordinates, so the final position is (81.63, 66.57) relative to the origin at Charleston. This is converted to distance and angle by ...
d = √(x² +y²) = √(81.63² +66.57²) = √11095.74 = 105.3 . . . nautical miles
α = arctan(66.57/81.63) = 39.2°
The bearing is 90° -α = 50.8°.
__
Additional comment
You may notice that our x-y coordinate solution measured the angles counterclockwise from the +x axis, the way angles are conventionally measured on an x-y plane. This requires we subtract the resulting angle from 90° in order to find the bearing.
On the other hand, our calculator solution (attachment 2) used bearing angles directly. If we were to convert these distance∠angle coordinates to rectangular coordinates, they would correspond to (north, east) coordinates, rather than the (east, north) coordinates of an (x, y) plane.
<95141404393>

Related Questions
Please answer ASAP !!!!!!!!!! Will mark brainliest !!!!!!!!!!!!!!

Answers
PLEASEEEE HELPPP I’m BEGGINGGG
When solving the following equation by completing the square, what would be your
first step?
x^2 - 6x – 40 = 0

Answers
Answer: Add 40 to both sides to collect like terms on each side of the equation
Step-by-step explanation: That's the first step
if fis a differentiable function of rand g(x,y) = f(xy), show that
Answers
g(x, y) = f(xy) is a differentiable function.
We'll show that g(x, y) = f(xy) is a differentiable function by finding its partial derivatives with respect to x and y.
Given that f is a differentiable function of r, we know that f'(r) exists for all values of r. Now, let's find the partial derivatives of g(x, y) with respect to x and y:
1. ∂g/∂x:
Using the chain rule, we get ∂g/∂x = (∂f/∂r) * (∂r/∂x). Since r = xy, ∂r/∂x = y. Thus, ∂g/∂x = f'(xy) * y.
2. ∂g/∂y:
Similarly, we get ∂g/∂y = (∂f/∂r) * (∂r/∂y). Since r = xy, ∂r/∂y = x. Thus, ∂g/∂y = f'(xy) * x.
Since both partial derivatives ∂g/∂x and ∂g/∂y exist, we can conclude that g(x, y) = f(xy) is a differentiable function.
For more such questions on Differentiable function.
https://brainly.com/question/30079101#
#SPJ11
what makes 3+7+2= +2true?
Answers
The equation 3+7+2=+2 is actually not true, but false.
Is the 3+7+2= +2true?The equation 3+7+2=+2 is actually not true, but false. This is because the sum of 3, 7, and 2 is 12, not 2.
In general, an equation is considered true if the expressions on both sides of the equal sign are equivalent in value. In this case, the expressions on the left-hand side (3+7+2) and the right-hand side (+2) are not equivalent, and therefore the equation is false.
Learn more about equation at https://brainly.com/question/14107099
#SPJ1
The ratio 5:11 can also be used to describe a relationship between the beads on each necklace. What relationship could this ratio describe? Show or explain how you got your answer.
Answers
The given ratio 5:11 can be used to describe a relationship between the beads on each necklace. The relationship that this ratio can describe is the relative number of beads of different colors.
Let’s see how this relationship was obtained:
We know that the ratio of 5:11 can be expressed in fraction form as 5/11.
Since there are two different colors of beads, let’s assume that there are 5 beads of one color (let’s call it color A) and 11 beads of another color (let’s call it color B).
Hence, the ratio of 5:11 can describe the relationship between the number of beads of color, A to the number of beads of color B on each necklace.
In other words, the ratio of 5:11 tells us that for every 5 beads of color A, there are 11 beads of color B.
This ratio can be used to describe the relative number of beads of different colors on the necklace.
To know more about ratio, visit ;
https://brainly.com/question/12024093
#SPJ11
Select the correct answer.What is the range of the function graphed below?у86-2-4HX- 224624-6OA - < y < -2

Answers
According to the graph, the range, which is the set of values that y can take, comes from negative infinite and stops at approximately 2. It means that y will always be greater than negative infinite but less than 2, this represented as inequation is:
\(-\inftyThe correct answer is B.Please explain how to do this and one answer.

Answers
Answer:
In counting to a base, when we get to the point where the base integer comes up, we replace by 10, on the first time and by 10 at every other time the integer is about to come up
We now this in base 10 as when we get to 10 we input 10 and so and so till we get to 99 where since we are in base 10 the next number is 100 because that is the highest we can go while in base 11 100 in base is equivalent to 91
So we have for base 5
1 , 2, 3, 4, 10, 11, 12, 13, 14, 20, 21, 22, 23, 24, 30, 31, 32, 33, 34, 40, 41, 42, 43, 44, 100, 101, 102, 103, 104, 110, 111, 112, 113, 114, 120, 121, 122, 123, 124, 130, 131, 132, 133, 134, 140, 141, 142, 143, 144, 200
We see that on getting to 4 instead of the next digit to be 5 we replace it with 10 because 5 cannot be displayed in base 5
Similarly after 14 is 20 because 5 cannot be displayed at 24 the next number is 30 because 5 cannot be displayed
at 34 the next 40, while at 44 the next is (we could have written 50 but 5 is 10 in base 5 so we write 100) 100
At 144, we note that 44 = 100 + 44, therefore, the next number will be 100 + 44+ 1 = 100 + (45 but 45 = 100 in base 5) 100 so that the next number is 200
Base 2
In base 2 we have;
1, 10, 11, 100, 101, 110, 111, 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111, 10000, 10001, 10010, 10011, 10100, 10101, 10110, 10111, 11000, 11001, 11010, 11011, 11100, 11101, 11110, 11111, 100000, 100001, 100010, 100011, 100100, 100101, 100110, 100111, 101000, 101001, 101010, 101011, 101100, 101101, 101110, 101111, 110000, 110001, 110010
We see that there are no 2s and after 11 we get 100 just like after 99 we get 100 in base 10 and after 44 we get 100 in base 5
So we need to still have an idea of the number system just as we did for base 10
Step-by-step explanation:
Solve the equation using the Quadratic Formula. x^{2}-11x-5=0
Answers
Solution of the equation x² -11x -5 =0 using quadratic formula is equal to x = (11 ±√141)/ 2 .
As given in the question,
Given equation is equal to
x² -11x -5 =0
Solving the given equation using quadratic formula we get,
Standard quadratic equation is
ax² + bx + c =0
D = √b² -4ac
D >0 two distinct roots.
Roots given by:
x = ( -b ± √b² -4ac) /2a
Here a = 1 , b= -11, c= -5
D = √ (-11)² -4(1)(-5)
= √121+20
=√141 >0
Two distinct roots.
x = (-(-11) ± √141) /2(1)
= (11 ±√141) /2
Therefore, Solution of the equation x² -11x -5 =0 using quadratic formula is equal to x = (11 ±√141)/ 2 .
Learn more about quadratic formula here
brainly.com/question/9300679
#SPJ1
Each histogram represents a set of data with a median of 29.5. Which set of data most likely has a mean that is closest to 29.5?
A graph shows the horizontal axis numbered 9 to 48. The vertical axis is numbered 1 to 5. The graph shows an upward trend from 1 to 33 then a downward trend from 33 to 45.
A graph shows the horizontal axis numbered 15 to 48. The vertical axis is numbered 1 to 5. The graph shows an upward trend from 1 to 30 then a downward trend from 30 to 45.
A graph shows the horizontal axis numbered 12 to 56. The vertical axis is numbered 2 to 8. The graph shows an upward trend from 1 to 32 then a downward trend from 32 to 56.
A graph shows the horizontal axis numbered 15 to 54. The vertical axis is numbered 1 to 5. The graph shows an upward trend from 1 to 24, a downward trend from 24 to 27, an upward trend from 27 to 30, a downward trend from 30 to 39, an upward trend from 39 to 45, a downward trend from 45 to 48, then an upward trend from 48 to 51.
Answers
To determine which set of data most likely has a mean closest to 29.5, we need to analyze the shape and position of the histograms in relation to the value 29.5.
Looking at the histograms described:
The first histogram ranges from 9 to 48, and the upward trend starts from 1 and ends at 33, followed by a downward trend. This histogram suggests that there may be values lower than 29.5, which would bring the mean below 29.5.
The second histogram ranges from 15 to 48, with an upward trend from 1 to 30 and then a downward trend. Similar to the first histogram, it suggests the possibility of values lower than 29.5, indicating a mean below 29.5.
The third histogram ranges from 12 to 56, and the upward trend starts from 1 and ends at 32, followed by a downward trend. This histogram covers a wider range but still suggests the possibility of values below 29.5, indicating a mean below 29.5.
The fourth histogram ranges from 15 to 54 and exhibits multiple trends. While it has fluctuations, it covers a wider range and includes both upward and downward trends. This histogram suggests the possibility of values above and below 29.5, potentially resulting in a mean closer to 29.5.
Based on the descriptions, the fourth histogram, with its more varied trends and wider range, is most likely to have a mean closest to 29.5.
For such more question on histograms
https://brainly.com/question/2962546
#SPJ8
33% part (c) if she drove back home using the same path she took out to the university and arrives 7.6 h after she first left home, what was her average speed for the entire trip, in kilometers per hour?
Answers
A student drove from her home to the university and get back to her home. The distance of her home and the university is 12 km. Her average speed for the entire trip is: 3.16 km/hours
The relation between speed, distance, and time is given by:
d = v x t
Where:
d = distance
v = speed
t = travelled time
In this problem, the distance of round trip, from her home to university and back home is:
d = 2 x 12 km = 24 km
The time needs to make this round trip = t = 7.6 hours
Hence, the average speed is:
average speed = distance/time
average speed = 24 / 7.6
average speed = 3.16 km/hours
Your question is incomplete. Most likely it was:
A student drove to the university from her home and noted that the odometer reading of her car increased by 12.0 km.
(c) if she drove back home using the same path she took out to the university and arrives 7.6 h after she first left home, what was her average speed for the entire trip, in kilometers per hour?
Learn more about average speed here:
https://brainly.com/question/4931057
#SPJ4
Help me please due in 5 minutes

Answers
Answer:
Step-by-step explanation:
(x - 8)/2 = -5
x - 8 = -10
x = -2
(y + 6)/2 = 10
y + 6 = 20
y = 14
(-2, 14)
습
John spends $94 to buy packages of cleaning supplies for a camp. He buys t packages of
towels, each package is $6 and contains 8 towels. He also buys s packages of soap; each
package is $4 and contains 10 bars of soap. John buys 20 packages of cleaning supplies
altogether. Write a system of equations to represent the packages of cleaning supplies John
buys
Answers
Answer:
B
Step-by-step explanation:
step
Pls help and SHOW WORKINGS....due ASAP

Answers
Answer:
(B). 50°
Step-by-step explanation:
(5x + 55)° = (2x + 100)°
5x + 55 = 2x + 100
5x - 2x = 100 - 55
3x = 45
x = 15
5(15) + 55 = 130°
m∠2 = 180° - 130° = 50°

Find the coordinates of the points of intersection of the parabola y=x^2+3x-4 and the line y=2x+2
Answers
x^2+3x-4=2x+2
x^2+x-6=0
(x+3)(x-2)=0
x=-3,2
So, these are the x values of the intersection. To get the y values, you can just plug them back into either formula:
y=2(-3)+2
y=-4
y2(2)+2
y=6
So the coordinates are (-3,-4) and 2,6).
On a number line, point A is at coordinate -2. Point B is at coordinate 0. Fine the coordinate that is the midpoint from A to B.
Answers
Answer:
The midpoint of the line segment AB
is at (−1, 0).
Step-by-step explanation:
Midpoint Formula:In a general sense the midpoint formula for a line segment whose endpoints are
\( \sf ( x_1 + x_2) (y_1 + y_2)\)
would be the mean of the abscissa and the ordinate as seen in the formula below:
\( \sf \: (x_m, \: y_m) = ( \frac{x_1 + x_2}{2} , \frac{y_1 + y_2}{2} )\)
When the line segment lies on one axis, then the there would be only one non-zero value in the ordered pair.
Assuming that the line segment AB
is in the x-axis, then the coordinates of the points would be:
\( \sf \: A(−2, 0)B(0,0)\)
To get the midpoint, substitute the points above in the formula for the midpoint:
\( \sf \: (x_m, \: y_m) = ( \frac{x_1 + x_2}{2} , \frac{y_1 + y_2}{2} ) \\ \sf \: = ( \frac{ - 2 + 0}{2} ),0 \\ \sf \: = ( \frac{ - 2}{2} ), 0 \: \: \: \: \: \: \: \: \\ \sf \: ( - 1, 0)\)
The midpoint of the line segment AB
is at (−1, 0).
Insert < >, or= to make the following sentence true.

Answers
Answer:
it would be “>”, 100% guaranteed.
Answer:
answer is >
Step-by-step explanation:
hope this is helpful
A car originally sold for $25,900. it depreciates exponentially at a rate of 8.2% per year. nina put $10,000 down and pays $550 per month to pay off the balance. after how
what will that value be?
many years will her car value equal the amount she paid for the car to that point?
Answers
After 1.8 years, the value equals the amount she paid for the car.
The value will be $ 22,131.10.
To solve the problem, find both the expense equation and depreciation equation.
The exponential depreciation equation will be:
\(y=25,900(1-0.082)^x\)
Where x represents time in years.
The expense equation will be: y=550 x+10,000
Where x represents the number of months that have passed
If x represents time in years in the expense equation, then it determines the yearly payment rather than the monthly payment.
Over the course of the year, Nina will have paid 550(12) or $ 6,600 in car payments.
The new yearly expense equation will be: y=6,600 x+10,000
Where x is time in years.
Use the two equations to find the point of intersection which will give the time she paid for the car and the value paid by her.
For more questions on Exponential depreciation equation
https://brainly.com/question/15261812
#SPJ4
Simplify problem: ∛-27n^27

Answers
Answer:
-3n⁹
Step-by-step explanation:
= \(\sqrt[3]{-27n^(27)}\)
= \(\sqrt[3]{-27} * \sqrt[3]{n^{27}}\)
= (-3) × n⁹
= -3n⁹
Question 1: Identify the number that does not belong with the other three. Explain your reasoning.
50. 1 , -50/2 , -50.1 , √50
Answers
Answer:
√50 is the odd one out.
Step-by-step explanation:
√50 is irrational while the others are rational.
Jutin chooe a function o that when he ue the number 7 a an input, the output i 20. Which function could he ue?
A. F(x)=2x5
B. G(x)=x^2-19
C. H(x)=13-x
D. J(x)=3x-1
HELP PLEASE!!!
Answers
Jutin chooses a function J(x) = 3x - 1 that when he uses the number 7 as an input, then the output is 20.
As per the given data, Jutin chooses a function in which he uses the number 7 as an input, then the output is 20.
Here we have to determine which function Jutin has to use.
Now we have to substitute the value that x = 7 in all the given functions.
First function:
F(x) = 2\(x^{5}\)
F(7) = 2 \((7)^{5}\)
F(7) = 2 (16807)
F(7) = 33614 which is not equal to 20.
Second function:
G(x) = \(x^{2}\) - 19
F(7) = \((7)^{2}\) - 19
F(7) = 49 - 19
F(7) = 30 which is not equal to 20.
Third function:
H(x) = 13 - x
H(7) = 13 - 7
H(7) = 6 which is not equal to 20.
Fourth function:
J(x) = 3x - 1
J(7) = 3(7) - 1
J(7) = 21 - 1
J(7) = 20
The correct function is J(x) = 3x - 1
For more questions on substitution method
https://brainly.com/question/28663522
#SPJ4
Ethan and Bob are having a skateboard race. Ethan began at the starting line
and rode at a constant rate of two feet per second. Bob had a fourteen-foot
head start and rode three feet every five seconds.
What's is the linear equation
Answers
Answer:
aa
Step-by-step explanation:
aa
Which set of measures could represent the lengths of the sides of a right triangle?
a
b
c
d

Answers
The expression (x - 6)2 is equivalent to
A. x2 - 36
B. x2 + 36
C. x2 - 12x + 36
D. x2 + 12x + 36
Answers
Answer:
x^2 -12x+36
Step-by-step explanation:
(x - 6)^2
(x-6)(x-6)
FOIL
x^2 - 6x-6x+36
Combine like terms
x^2 -12x+36
Multiplying a measure
by a scale to produce a
reduced or enlarged
measure
Answers
Answer:
we conclude that:
If the scale factor > 1, the image is stretchedIf the scale factor < 1, the image is reducedIf the scale factor = 1, the image and object will be congruentStep-by-step explanation:
A dilation is a transformation which generates an image that is the same shape as the original object but in a different size.
The image can be obtained by multiplying the measure of the original object by a scale factor.
If the scale factor > 1, the image is stretched
If the scale factor < 1, the image is reduced
If the scale factor = 1, the image and object will be congruent
For example, if we multiply the measure of the coordinates of the vertex A(2, 2) of a triangle by a scale factor of 2, the image A' is stretched as the scale factor > 1.
Dilation with scale factor 2, multiply by 2.
(x, y) → (2x, 2y)A(2, 2) → (2(2), 2(2)) = A'(4, 4)
So, the image point A'(4, 4) is enlarged.
Dilation with scale factor ½, multiply by ½.
(x, y) → (½x, ½y )A(2, 2) → (2(1/2), 2(1/2)) = A'(1, 1)
So, the image point A'(1, 1) is reduced.
Therefore, we conclude that:
If the scale factor > 1, the image is stretchedIf the scale factor < 1, the image is reducedIf the scale factor = 1, the image and object will be congruentJack's bill at a restaurant came to $51.31 he wants to leave a 15% tip how much will the new total be including tip
Answers
The new total bill including the tip of 15% is $59.01.
Calculating the new bill including the tipTo find the amount of the tip, we can multiply the total bill by the percentage as a decimal:
tip = 0.15 * $51.31 = $7.70
To find the new total including the tip, we can add the tip to the original bill:
new total = $51.31 + $7.70 = $59.01
So the new total, including a 15% tip, will be $59.01.
Read more about sales tax at
https://brainly.com/question/9437038
#SPJ1
please, please help me with this!! it’s very important.

Answers
The parabola's vertex is located at (-2, 8). The parabola's graph is then depicted below.
Let a be the leading coefficient and the parabola's vertex be the point (h, k). The parabola's equation will therefore be stated as,
y = a(x - h)² + k
The parabola's equation is stated as,
y = -(x + 2)² + 8
The downward-pointing parabola is represented by the negative sign.
The vertex of the parabola is at (-2, 8), according to the equation above. The parabola's graph is then depicted below.
More about the equation of the parabola link is given below.
https://brainly.com/question/20333425
#SPJ1

If mWP= 56° and mKA= 162°, find m E.

Answers
Answer:
m<E = 1/2 ( WP - KA )
m<E = 1/2 ( 162 -56 )
m<E = 1/2 (106)
m<E = 53
PLEASE HELP!!!!!!!!!!!

Answers
Answer:
1: The ladder
2:
3:
Step-by-step explanation:
How many seconds does it take a bike traveling at 20km/hour to travel 100 meters?
Answers
It takes approximately 18.001 seconds (or approximately 18 seconds) for the bike traveling at 20 km/h to cover a distance of 100 meters.
To determine how many seconds, it takes for a bike traveling at 20 km/h to cover a distance of 100 meters, we need to convert the speed from kilometers per hour to meters per second and then calculate the time.
First, let's convert the speed from kilometers per hour to meters per second.
1 kilometer is equal to 1000 meters, and 1 hour is equal to 3600 seconds.
Speed in meters per second = (20 km/h) * (1000 m/km) / (3600 s/h)
Calculating:
Speed in meters per second = (20 * 1000) / 3600 ≈ 5.556 m/s
Now that we have the speed in meters per second, we can calculate the time it takes to travel 100 meters using the formula:
Time = Distance / Speed
Time = 100 m / 5.556 m/s
Calculating:
Time ≈ 18.001 seconds
Therefore, it takes approximately 18.001 seconds (or approximately 18 seconds) for the bike traveling at 20 km/h to cover a distance of 100 meters.
Learn more about distance from the given link
https://brainly.com/question/26550516
#SPJ11
Instructions: For the given discriminant, state the number and type of solutions.

Answers
If the discriminant is negative, then neither of the solutions is a real number.
Since the discriminant is a negative number 7, then there is/are no real solutions to the quadratic equation.