Answers
The measurements of <a is 105^o, and <b is 75^o.
What are supplementary angles?Two or more angles are said to be supplementary if their measures add up to 180^o.
In the given diagram, we have;
a. To find the measure of <a;
m<a + 40 + 35 = 180
m<a + 75 = 180
m<a = 180 - 75
= 105
m<a = 105^o
b. To find the measure of <b;
m<b + m<a = 180
m<b + 105 = 180
m<b = 180 - 105
= 75
m<b = 75^o
Learn more about supplementary angles at https://brainly.com/question/26760105
#SPJ1
Related Questions
PLEASE HELP
which mapping diagram does NOT represent function from x-y

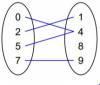


Answers
Answer:
Diagram 1
Step-by-step explanation:
This diagram does not represent a function because the x value 6 is outputting 2 different y values, 4 and 6. This goes directly against the rules of a function.
Daily high temperatures in St. Louis for the last week were as follows: 92, 92, 93, 95, 95, 86, 95 (yesterday). a) The high temperature for today using a 3-day moving average =____ degrees (round your response to one decimal place).
Answers
The high temperature for today using a 3-day moving average is 92 degrees.
To calculate the high temperature for today using a 3-day moving average, we take the average of the temperatures from the past three days, including today.
Given the daily high temperatures in St. Louis for the last week:
92, 92, 93, 95, 95, 86, 95 (yesterday)
To find the 3-day moving average for today's high temperature, we consider the temperatures from yesterday, the day before yesterday, and three days ago.
(95 + 86 + 95) / 3 = 92
Therefore, the high temperature for today, calculated using a 3-day moving average, is approximately 92 degrees Fahrenheit, rounded to one decimal place.
Learn more about high temperature here:-
https://brainly.com/question/28708675
#SPJ11
Last year, Amy opened an investment account with $6800. At the end of the year, the amount in the account had increased by 23.5%. How much is this increase in dollars? How much money was in her account at the end of last year?
Answers
Answer:
-The increase in dollars is $1598
-The amount in her account at the end of last year was $8398.
Step-by-step explanation:
To find the increase, you have to multiply the initial amount for the percentage increase:
6800*23.5%=1598
Now, to find the amount in her account at the end of last year, you have to add the initial amount plus the increase in dollars:
6800+1598=8398
According to this, the amount in her account at the end of last year was $8398.
48:PLEASE HELP Find the x-intercept of -x+2y=22
Answers
Answer:
-22
Step-by-step explanation:
set y equal to zero and solve like a regular singular variable equation
926 divided by 38 is equal to 10+10+2+2 with a remainder
Answers
In a free-throw contest, three players take the same number of shots. Player A makes 47 of 55 shots. Player B makes 0.84 of his shots. Player
makes 87% of her shots. Who wins?
O Player A
O Player B
O Player
O A and C tie.
Answers
Answer:
Player C
Step-by-step explanation:
Player A:
He made 47 of his 55 shots.
In percentage, this translates to;
47/55 × 100% = 85.45%
Player B: conversion ratio = 0.84
In percentage, this translates to 84%
Player C:
She made 87% of her shots
Player C had the highest conversion percentage and is thus the winner
if 2x – 1 is a factor of 16x4
24x3 + 2x + f, find f.
Answers
Answer:
f = -5
Step-by-step explanation:
If 2x – 1 is a factor of 16x4 + 24x3 + 2x + f, find f.
If 2x - 1 = 16x⁴ + 24x³ + 2x + f, find f.
2x - 1 = 0
2x = 1
x = 1/2
Hence
f(1/2) = 16(1/2)⁴ + 24(1/2)³ + 2(1/2) + f
= 16(1/16) + 24(1/8) + 1 + f
= 1 + 3 + 1 + f
= 5+ f
f = -5
\( \sqrt{28} \)simplest radical form
Answers
Recall following property of radicals:
\(\sqrt[]{a\cdot b}=\sqrt[]{a}\cdot\sqrt[]{b}\)Since 28 can be factorized as:
\(2^2\cdot7\)Use the property previoulsy mentioned to rewrite the square root of 28:
\(\begin{gathered} \sqrt[]{28}=\sqrt[]{2^2\cdot7} \\ =\sqrt[]{2^2}\cdot\sqrt[]{7} \\ =2\cdot\sqrt[]{7} \end{gathered}\)Therefore, the simplest radical form of the square root of 28, is:
\(2\cdot\sqrt[]{7}\)the mean of a distribution is defined as the data value where 50% of the data is above and 50% is below. group of answer choices true false
Answers
FALSE, it is not the mean but the median of a distribution which is defined as the data value where 50% of the data is above and 50% is below.
The median denotes the point at which 50% of data values are higher and 50% are lower. As a result, it is the data's midpoint. In a symmetrical distribution, the median is always the midpoint, resulting in a mirror image with the median in the center.
The median is the number in the middle of a sorted, ascending or descending list of numbers, and it might be more descriptive of the data set than the average.
To know more about median refer to:
brainly.com/question/28060453
#SPJ4
What is the vertex of the quadratic function below?
y=x² +12%-7
O A. (-6,-43)
OB. (-6,-29)
O C. (6,3)
OD. (6,29)
Answers
Answer:
A
Step-by-step explanation:
assuming you meant y = x² + 12x - 7 , then
given a quadratic in standard form
y = ax² + bx + c (a ≠ 0 )
the x- coordinate of the vertex is
x = - \(\frac{b}{2a}\)
y = x² + 12x - 7 ← is in standard form
with a = 1 , b = 12 , then x- coordinate of vertex is
x = - \(\frac{12}{2}\) = - 6
substitute x = - 6 into the equation for corresponding y- coordinate
y = (- 6)² + 12(- 6) - 7
= 36 - 72 - 7
= - 43
vertex = (- 6, - 43 )
Help i dont get this one ASAP

Answers
The number of ways is 1 billion.
We are asked to determine the possible number of ways of the social security number that is 9 digits if the numbers can be repeated.
In this case, using fundamental counting, there are 10 possible numbers in each digit that is from zero to nine.
Thus, the number of ways is 10*10*10*10*10*10*10*10*10 equal to 1 billion ways.
Hence the number of ways is 1 billion.
Learn more about fundamental counting click;
https://brainly.com/question/28384306
#SPJ1
please help!! giving brainliest!!

Answers
Answer:
neither
Step-by-step explanation:
it is actually geometric sequence
What is the perimeterABC is shown on the grid.9 +27 unitsB11490 9+27 units9+ I units9+VT units
Answers
We have three points that represent the vertices of the triangle
- A( -1, 5 )
- B( 4, 5 )
- C( -1, 1 )
We need to calculate the distances between the points to calculate the perimeter
To calculate the distances we must use the next equation
\(d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}\)Distance for AB:
\(\begin{gathered} d_1=\sqrt[]{(4-(-1))^2+(5-5)^2} \\ d_1=\sqrt[]{5^2+0^2}=\sqrt[]{5^2}=5 \end{gathered}\)Distance for BC:
\(\begin{gathered} d_2=\sqrt[]{(-1-4)^2+(1-5)^2} \\ d_2=\sqrt[]{(-5)^2+(-4)^2}=\sqrt[]{41} \end{gathered}\)Distance for AC:
\(\begin{gathered} d_3=\sqrt[]{(-1-(-1))^2+(1-5)^2} \\ d_3=\sqrt[]{0^2+(-4)^2}=\sqrt[]{16}=4 \end{gathered}\)Finally, the perimeter is
\(\begin{gathered} S=d_1+d_2+d_3 \\ S=5+\sqrt[]{41}+4 \\ S=9+\sqrt[]{41} \end{gathered}\)So, the answer is
\(9+\sqrt[]{41}\text{ units}\)Explain the difference between the z-test for mu using rejection region(s) and the z-test for p using a P-value.
Choose the correct answer below.
a. The z-test using rejection region(s) is used when the population is normal. The z-test using a P-value is used when the population is not normal.
b. In the z-test using rejection region(s), the test statistic is compared with the level of significance alpha. The z-test using a P-value compares the P-value with the critical values.
c. The z-test using rejection region(s) is used when the population is not normal. The z-test using a P-value is used when the population is normal.
d. In the z-test using rejection region(s), the test statistic is compared with critical values. The z-test using a P-value compares the P-value with the level of significance a.
Answers
The difference lies in the comparison made: critical values in the z-test using rejection region(s) and the P-value in the z-test using a P-value. The choice between the two approaches depends on the nature of the population and the specific hypothesis being tested.
The correct answer is (d): In the z-test using rejection region(s), the test statistic is compared with critical values. The z-test using a P-value compares the P-value with the level of significance alpha.
The z-test is a statistical test used to assess whether a sample mean or proportion significantly differs from a hypothesized population mean or proportion. The difference between the z-test for mu (population mean) using rejection region(s) and the z-test for p (population proportion) using a P-value lies in the approach used to make the inference.
In the z-test using rejection region(s), the test statistic (calculated from the sample) is compared with critical values based on the chosen level of significance alpha. The critical values are determined from the standard normal distribution or a z-table, and if the test statistic falls within the rejection region (beyond the critical values), the null hypothesis is rejected.
On the other hand, in the z-test for p using a P-value, the test statistic is compared with the P-value. The P-value represents the probability of observing a test statistic as extreme or more extreme than the one obtained, assuming the null hypothesis is true. If the P-value is smaller than the chosen level of significance alpha, the null hypothesis is rejected.
Therefore, the difference lies in the comparison made: critical values in the z-test using rejection region(s) and the P-value in the z-test using a P-value. The choice between the two approaches depends on the nature of the population and the specific hypothesis being tested.
Learn more about critical values
https://brainly.com/question/14040224
#SPJ11
1c - 20 = 4 - 3c pls help fast in school rn
Answers
Answer:
4c-20= 4
+20 +20
4c= 24
/4 /4
c= 6
Answer:
c = 1 btw can i be brainiest...
Step-by-step explanation:
First, rewrite the left side of the equation and group and combine like terms:
c + (4 − 3c) − 2 = 0
c + 4 − 3c − 2 = 0
−3c + c + 4 − 2 = 0
−3c + 1c + 4 − 2 = 0
(−3 + 1) c + (4 - 2) = 0
−2c + 2 = 0
Next, subtract
2
from each side of the equation to isolate the
c
term while keeping the equation balanced:
−2c + 2 − 2 = 0
−2 − 2c + 0 = −2
−2c = −2
Now, divide each side of the equation by
−2
to solve for
c
while keeping the equation balanced:
−2c - 2 = −2 − 2
−2c − 2 = 1
c = 1
Let abcdef be a convex hexagon. let a', b', c', d', e', f' be the centroids of triangles fab, abc, bcd, cde, def, efa, respectively.
(a) show that every pair of opposite sides in hexagon a'b'c'd'e'f' (namely a'b' and d'e', b'c' and e'f', and c'd' and f'a') are parallel and equal in length.
(b) show that triangles a'c'e' and b'd'f' have equal areas.
Answers
(a) shows that every pair of opposite sides in the hexagon a′b′c′d′e′f′ are parallel and equal in length. On the other hand, (b) demonstrates that the triangles a′c′e′ and b′d′f′ have equal areas.
(a) To show that every pair of opposite sides in hexagon a'b'c'd'e'f' are parallel and equal in length, we can use the fact that the centroids of triangles divide the medians into segments of equal length.
Let's consider a'b' and d'e'. The centroid of triangle fab, a', divides the median fb into two segments, a'f and a'b', such that a'f = 2/3 * fb. Similarly, the centroid of triangle def, e', divides the median de into two segments, e'd and e'f', such that e'd = 2/3 * de.
Since fb = de (opposite sides of hexagon abcdef), we have a'f = e'd. Now, we can consider the triangles a'f'd' and e'df'. By the properties of triangles, we know that if two sides of a triangle are equal, and the included angles are equal, then the triangles are congruent.
In this case, a'f' = e'd' (as shown above) and angle a'f'd' = angle e'df' (corresponding angles). Therefore, triangle a'f'd' is congruent to triangle e'df'.
By congruence, the corresponding sides a'd' and e'f' are equal in length.
By similar reasoning, we can show that b'c' and e'f', as well as c'd' and f'a', are parallel and equal in length.
(b) To show that triangles a'c'e' and b'd'f' have equal areas, we can use the fact that the area of a triangle is one-half the product of its base and height.
In triangle a'c'e', the base is c'e' and the height is the perpendicular distance from a' to c'e'. Similarly, in triangle b'd'f', the base is d'f' and the height is the perpendicular distance from b' to d'f'.
Since opposite sides in hexagon a'b'c'd'e'f' are parallel (as shown in part (a)), the perpendicular distance from a' to c'e' is equal to the perpendicular distance from b' to d'f'.
Therefore, the heights of triangles a'c'e' and b'd'f' are equal. Additionally, the bases c'e' and d'f' are equal (as shown in part (a)).
Using the area formula, area = 1/2 * base * height, we can see that the areas of triangles a'c'e' and b'd'f' are equal.
Hence, we have shown that triangles a'c'e' and b'd'f' have equal areas.
Learn more about centroid here https://brainly.com/question/29148732
#SPJ11
Help me out and show me the full solution on how you solved it, please!

Answers
The value of each trigonometric identity is:
3/2
5/6
14/3
We have,
We will use the trigonometric formula and substitute the given values.
So,
Cosec θ
This can be written as,
= 1/ sin θ
= 1/(2/3)
= 3/2
And,
Sin θ
This can be written as,
= 1/ cosec θ
= 1/(6/5)
= 5/6
And,
Sec θ
This can be written as,
= 1/cosθ
= 1/(3/14)
= 14/3
Thus,
The value of each trigonometric identity is:
3/2
5/6
14/3
Learn more about trigonometric identities here:
https://brainly.com/question/14746686
#SPJ1
A cylindrical gasoline tank 4 feet in diameter and 5 feet long is carried on the back of a truck and used to fuel tractors. The axis of the tank is horizontal. The opening on the tractor tank is 5 feet above the top of the tank in the truck. Find the work done in pumping the entire contents of the fuel tank into the tractor
Answers
To find the work done in pumping the entire contents of the fuel tank into the tractor, we need to calculate the potential energy difference between the initial position of the gasoline in the truck's tank and its final position in the tractor's tank.
Given:
- Diameter of the cylindrical gasoline tank: 4 feet
- Length of the cylindrical gasoline tank: 5 feet
- Opening on the tractor tank is 5 feet above the top of the tank in the truck
First, let's calculate the volume of the cylindrical gasoline tank using the formula for the volume of a cylinder:
Volume = π * (radius^2) * height
The radius of the tank is half the diameter, so the radius is 4 feet / 2 = 2 feet.
Volume = π * (2^2) * 5 = 20π cubic feet
Since the entire contents of the fuel tank need to be pumped, the volume of gasoline to be pumped is 20π cubic feet.
To calculate the work done in pumping the gasoline, we need to find the vertical height through which the gasoline is lifted. This height is the sum of the height of the tank and the distance between the top of the tank and the opening on the tractor tank.
Height = 5 feet + 5 feet = 10 feet
The work done in pumping the gasoline can be calculated using the formula:
Work = Force × Distance
In this case, the force is the weight of the gasoline, and the distance is the height through which it is lifted. To calculate the weight of the gasoline, we need to know the density of gasoline. The density of gasoline can vary, but an average value is around 6.3 pounds per gallon.
Let's convert the volume of gasoline from cubic feet to gallons:
1 cubic foot = 7.48052 gallons (approximately)
Volume in gallons = 20π * 7.48052 ≈ 149.61π gallons
Weight of gasoline = Volume in gallons * Density of gasoline
Assuming the density of gasoline as 6.3 pounds per gallon:
Weight of gasoline = 149.61π * 6.3 ≈ 940.06π pounds
Finally, we can calculate the work done:
Work = Weight of gasoline * Height
Work = 940.06π * 10 ≈ 9400.6π foot-pounds
Therefore, the work done in pumping the entire contents of the fuel tank into the tractor is approximately 9400.6π foot-pounds.
Learn more about Work here:
https://brainly.com/question/29050812
#SPJ11
use a venn diagram to illustrate the relationship a ⊆ b and b ⊆ c.
Answers
Here is a Venn diagram illustrating the relationship between the sets a, b, and c, where a is a subset of b and b is a subset of c:
_______________
| c |
| |
| _________
| | |
| | b |
| | |
| |______ |
| | |
| a |__|
|_______________|
In this diagram, the set c is represented by the outer rectangle, the set b is the area inside the rectangle but outside the inner circle, and the set a is the area inside both the rectangle and the inner circle.
Since a is a subset of b, every element in a is also in b, and therefore the inner circle is entirely contained within the area representing b.
Similarly, since b is a subset of c, every element in b is also in c, and therefore the area representing b is entirely contained within the outer rectangle representing c.
This diagram shows that if a is a subset of b and b is a subset of c, then a is also a subset of c.
To know more about Venn diagram refer here:
https://brainly.com/question/20795347#
#SPJ11
Express 1.32 bar on 32 + 0.35 bar on 35
Answers
1.32 (bar on 32) + 0.35 (bar on 35) is equal to 166/99 in the simplest form.
To express 1.32 (bar on 32) + 0.35 (bar on 35) in fractional form, we can use the following steps:
Step 1: Let x = 1.32 (bar on 32)
So, x = 1.323232... (since the bar notation indicates that the digits after the bar repeat infinitely).
This means that 100x = 132.323232...
Step 2: Subtract x from 100x to eliminate the repeating decimal:
100x - x = 132.323232... - 1.323232...
99x = 131
x = 131/99
Step 3: Let y = 0.35 (bar on 35)
So, y = 0.353535...(since the bar notation indicates that the digits after the bar repeat infinitely).
This means that 10y = 3.5
Step 4: Subtract y from 100y to eliminate the repeating decimal:
100y = 35.353535...
100y - y = 35.3535... - 0.3535..
99y = 35
y = 35/99
Step 5: Add x and y to get the sum in the fractional form:
1.32 + 0.35 = (131/99) + (35/99)
Step 6: Simplify the sum by finding a common denominator and adding the numerators:
1.32 + 0.35 = (131/99) + (35/99)
1.32 + 0.35 = 166/99
Therefore, 1.32 (bar on 32) + 0.35 (bar on 35) is equal to 166/99 in the simplest form.
The question was Incomplete, Find the full content below :
Express 1.32 (bar on 32) + 0.35 (bar on 35) as a fraction in the simplest form
Know more about Simplest form here :
https://brainly.com/question/564834
#SPJ11
Expand and simplify 3(x + 4 ) +2 (x + 5) quickly please
Answers
Answer : 5x + 32
Step-by-step explanation:
3(x + 4 ) +2 (x + 5)
3x + 12 + 2x + 10
5x + 32
5x +32
An object of mass 480 kg is in free fall in a vacuum where there is no air resistance. Determine the acceleration of the object.
Answers
Since the object is in free fall the acceleration of the object is approximately
\(_{}9.81ms^{-2}\)What is 3 percent of 98
Answers
Answer:
2.94
Step-by-step explanation:
I just found 1%
Which is 0.98
then times that by 3 which is 2.94
hope that helps!
What is (1.8d − 3)(1.4) ???
Answers
The solution to the expression given as (1.8d − 3)(1.4) is 2.52d − 4.2
What are expressions?Expressions are mathematical statements that are represented by variables, coefficients and operators
How to evaluate the expression?From the question, we have the following expression that can be used in our computation:
(1.8d − 3)(1.4)
Remove the brackets in the above expression
So, we have the following representation
(1.8d − 3)(1.4) = 1.8d * 1.4 − 3 * 1.4
Evaluate the products
This gives
(1.8d − 3)(1.4) = 2.52d − 4.2
The above expression cannot be further simplified
Hence, the solution is 2.52d − 4.2
Read more about expressions at
https://brainly.com/question/15775046
#SPJ1
What is the area of this triangle

Answers
Answer:
17.5 units
Step-by-step explanation:
im not good at explaining sorry
graph it pleaseeeeeeeeeeeeeeeeeeeeeeeeeeee

Answers
Answer:
Step-by-step explanation:
5c + 4f ≥ 200
c + f ≤ 60
c > 0
f > 0

someone please help.


Answers
The completed table with regards to terms of an expression are presented as follows;
Condition \({}\) (6·x + 3) + (5·x - 4) (-4·y - 16) - 8·y + 10 + 2·y
Exactly 3 terms N/A \({}\) N/A
Exactly 5 terms N/A \({}\) N/A
Includes a zero pair No \({}\) No
Uses distributive property No No
Includes a negative factor No
Has no like terms False False
Condition \(8 - \dfrac{1}{2} \cdot \left(4 \cdot x - \dfrac{1}{2} + 12\cdot x -\dfrac{1}{4} \right)\) 0.25·(8·m - 12) - 0.5·(-4·m + 2)
Exactly 3 terms No \({}\) No
Exactly 5 terms Yes \({}\) \({}\) No
Includes a zero pair No \({}\) \({}\) Yes
Uses the distributive property Yes \({}\) Yes
Includes a negative factor Yes \({}\) Yes
Has no like terms No \({}\) No
What is a mathematical expression?A mathematical expression is a collection of variables and numbers along with mathematical operators which are all properly arranged.
The details of the conditions in the question are as follows;
Terms of an expression
A term is a subunit of an algebraic expression which are joined together by operators such as addition or subtraction
Zero pair
A zero pair are two numbers that when added together have a zero result
Distributive property
The distributive property of multiplication states that the multiplication of a number or variable by an addend is equivalent to the sum of the multiplication of the number or variable and each member of the addend
Negative factor
A negative factor is a factor that has a negative sign prefix
Like terms
Like terms are terms consisting of identical variables with the same powers of the variable
Learn more about expressions here:
https://brainly.com/question/1859113
#SPJ1
Giving brainlist
Solve for x: x ÷ 7 = 16
Answers
Answer:
x=112
Step-by-step explanation:
\(\frac{x}{7} =16\)
x=16*7
x=112
Answer: x = 112
Step-by-step explanation: To solve this equation for x,
I would first change x ÷ 7 to x/7 to make it easier to visualize.
So we have \(\frac{x}{7} = 16\).
Since x is being divided by 7, we multiply both sides by 7.
On the left, hat gives us x and on the right, 16 x 7 is 112.
So we have x = 112.
please help me you guys can do some but please help
Question 1(Multiple Choice Worth 2 points)
(Appropriate Measures MC)
A charity needs to report its typical donations received. The following is a list of the donations from one week. A histogram is provided to display the data.
1, 1, 6, 10, 10, 11, 12, 14, 15, 18, 20, 20, 20, 20, 20
A graph titled Donations to Charity in Dollars. The x-axis is labeled 1 to 5, 6 to 10, 11 to 15, and 16 to 20. The y-axis is labeled Frequency. There is a shaded bar up to 2 above 1 to 5, up to 3 above 6 to 10, up to 4 above 11 to 15, and up to 6 above 16 to 20.
Which measure of center should the charity use to accurately represent the data? Explain your answer.
The median of 14 is the most accurate to use, since the data is skewed.
The mean of 13.2 is the most accurate to use, since the data is skewed.
The median of 13.2 is the most accurate to use to show that they need more money.
The mean of 14 is the most accurate to use to show that they have plenty of money.
Question 2(Multiple Choice Worth 2 points)
(Appropriate Measures MC)
The box plot represents the number of tickets sold for a school dance.
A horizontal line labeled Number of Tickets sold that starts at 11, with tick marks every one unit up to 25. The graph is titled Tickets Sold for A Dance. The box extends from 17 to 20 on the number line. A line in the box is at 19. The lines outside the box end at 12 and 24.
Which of the following is the appropriate measure of variability for the data, and what is its value?
The IQR is the best measure of variability, and it equals 3.
The range is the best measure of variability, and it equals 12.
The IQR is the best measure of variability, and it equals 12.
The range is the best measure of variability, and it equals 3.
Question 3(Multiple Choice Worth 2 points)
(Appropriate Measures MC)
The table shows the length, in inches, of fish in a pond.
15 18 9 22
7 15 10 18
Determine if the data contains any outliers. If so, list the outliers.
There is an outlier at 22.
There is an outlier at 7.
There are outliers at 7 and 22.
There are no outliers.
Question 4(Multiple Choice Worth 2 points)
(Appropriate Measures MC)
The scores earned in a flower-growing competition are represented in the stem-and-leaf plot.
0 5
1 0, 3, 7
2 4, 6, 8
3 2
4
5 8
Key: 5|8 means 58
What is the appropriate measure of variability for the data shown, and what is its value?
The range is the best measure of variability, and it equals 18.5.
The IQR is the best measure of variability, and it equals 45.
The range is the best measure of variability, and it equals 45.
The IQR is the best measure of variability, and it equals 18.5.
Question 5(Multiple Choice Worth 2 points)
(Appropriate Measures MC)
The table shows the number of goals made by two hockey players.
Player A Player B
2, 3, 1, 3, 2, 2, 1, 3, 6 1, 4, 5, 1, 2, 4, 5, 5, 11
Find the best measure of variability for the data and determine which player was more consistent.
Player B is the most consistent, with an IQR of 3.5.
Player B is the most consistent, with a range of 10.
Player A is the most consistent, with an IQR of 1.5.
Player A is the most consistent, with a range of 5.
Question 7(Multiple Choice Worth 2 points)
(Appropriate Measures MC)
The line plot displays the number of roses purchased per day at a grocery store.
A horizontal line starting at 1 with tick marks every one unit up to 10. The line is labeled Number of Rose Bouquets, and the graph is titled Roses Purchased Per Day. There is one dot above 1 and 10. There are two dots above 6, 7, and 9. There are three dots above 8.
Which of the following is the best measure of center for the data, and what is its value?
The mean is the best measure of center, and it equals 8.
The median is the best measure of center, and it equals 7.3.
The mean is the best measure of center, and it equals 7.3.
The median is the best measure of center, and it equals 8.
Answers
Answer:
Step-by-step explanation:
The correct answer is: The median of 14 is the most accurate to use, since the data is skewed.
Explanation: Since the data is skewed to the right, meaning there are some larger donations that pull the mean up, the median is a more accurate measure of center. It represents the middle value of the data when it is ordered from smallest to largest, and is not affected by extreme values.
The correct answer is: The IQR is the best measure of variability, and it equals 3.
Explanation: The IQR (interquartile range) is the best measure of variability for this data because it shows the range of the middle 50% of the data. The range, which is the difference between the minimum and maximum values, is affected by outliers and extreme values. In this case, the IQR is equal to 20-17=3.
The correct answer is: There is an outlier at 22.
Explanation: To determine if there are outliers in the data, we can use the rule: an outlier is any value more than 1.5 times the IQR below the first quartile or above the third quartile. The first quartile is 9.5 and the third quartile is 18, so the IQR is 18-9.5=8.5. Therefore, any value less than 9.5-1.5(8.5)= -4.25 or greater than 18+1.5(8.5)=30.25 would be considered an outlier. The value of 22 is greater than 30.25, so it is an outlier.
The correct answer is: The IQR is the best measure of variability, and it equals 18.5.
Explanation: The IQR (interquartile range) is the best measure of variability for this data because it shows the range of the middle 50% of the data. The range, which is the difference between the minimum and maximum values, is affected by outliers and extreme values. In this case, the IQR is equal to the difference between the third quartile (25) and the first quartile (6.5), which is 18.5.
The correct answer is: Player A is the most consistent, with an IQR of 1.5.
Explanation: The IQR (interquartile range) is the best measure of variability for this data because it shows the range of the middle 50% of the data. To find the IQR, we first need to find the first and third quartiles. For Player A, the first quartile is 2 and the third quartile is 3, so the IQR is 3-2=1. For Player B, the first quartile is 2 and the third quartile is 5, so the IQR is 5-2=3.
The correct answer is: The median is the best measure of center, and it equals 7.3.
Explanation: Since the data is not strongly skewed, either the mean or the median could be used as a measure of center. However, the median is often preferred because it is less affected by extreme values. The median for this data is the value that is in the middle when the data is ordered from smallest to largest. In this case, we have 10 data points, so the median is the average of the 5th and 6th values, which are both equal to 7. Therefore, the median is 7, and not 7.3. The mean is also 7.3, but it is affected by the extreme values.
Answer:
See below, please.
Step-by-step explanation:
Question 1
The median of 14 is the most accurate to use, since the data is skewed.
Question 2
The IQR is the best measure of variability, and it equals 3.
Question 3
There is an outlier at 22.
Question 4
The IQR is the best measure of variability, and it equals 18.5.
Question 5
Player A is the most consistent, with an IQR of 1.5.
Question 7: The median is the best measure of center, and it equals 7.3.
Y=400(.99)^x is this growth or decay
Answers
Answer:
its decreasing. .........
The given function of the growth decay is decreasing.
We have given that,
Y=400(.99)^x
When does growth decay increase or decrease?
Exponential growth is a process that increases quantity over time. decreases over time, and is said to be undergoing exponential decay instead.
Therefore, The given function of the growth decay is decreasing.
To learn more about the decay visit:
https://brainly.com/question/7920039
#SPJ2
