Death Valley, California, has an elevation of -282 feet. What does this mean?
Answers
Answer:
Step-by-step explanation:
It is below groung level
Answer: that if sombody falls you know where it leads... there DEATH
Step-by-step explanation:
Related Questions
An underwater observation tower is being built with circular viewing portholes enabling visitors to see underwater life. Each vertically oriented porthole is to have a 3 ft diameter whose center is to be located 50 ft underwater. Find the total fluid force exerted on each porthole. Also, compute the fluid force on a horizontally oriented porthole that is under 50 ft of water.
Answers
The total fluid force exerted on each vertically oriented porthole with a 3 ft diameter and a center located 50 ft underwater is approximately 28,274 pounds. The fluid force on a horizontally oriented porthole under 50 ft of water is also approximately 28,274 pounds.
The pressure at a given depth in a fluid is given by the equation P = ρgh, where P is the pressure, ρ is the density of the fluid, g is the acceleration due to gravity, and h is the depth.
In this case, the depth of the vertically oriented porthole is 50 ft. We assume the density of water to be approximately 62.4 pounds per cubic foot, and the acceleration due to gravity is approximately 32.2 ft/s². Plugging these values into the equation, we can calculate the pressure at the depth of the porthole:
P = (62.4 lb/ft³) * (32.2 ft/s²) * (50 ft) = 100,080 lb/ft²
To find the fluid force exerted on the porthole, we need to multiply the pressure by the area of the porthole. The area of circle is given by the formula A = πr², where r is the radius of the circle. In this case, the radius is half the diameter, which is 1.5 ft. Thus, the area of the porthole is:
A = π * (1.5 ft)² = 7.07 ft²
Now, we can calculate the fluid force:
Fluid Force = Pressure * Area = 100,080 lb/ft² * 7.07 ft² ≈ 28,274 lb
Therefore, the total fluid force exerted on each vertically oriented porthole is approximately 28,274 pounds.
For the horizontally oriented porthole under 50 ft of water, the fluid force would be the same as the vertically oriented porthole. Hence, the fluid force on the horizontally oriented porthole is also approximately 28,274 pounds.
Learn more about area of circle here:
https://brainly.com/question/28642423
#SPJ11
km of 2km,1km,2km,3km,3km,6km
Answers
An office building worth $1 million when completed in 1997 was depreciated linearly over 50 years; that is, the book value of the building decreases at a constant rate, so that at the end of 50 years the book value is zero.
What was the book value, in dollars, of the building in 2013?
$
What will be the book value, in dollars, in 2017?
$
What will be the book value, in dollars, in 2025?
$
Answers
The book value of the office building in 2013 is $320,000; the book value of the office building in 2017 is $400,000, and the book value of the office building in 2025 is $560,000.
Given that an office building worth $1 million when completed in 1997 was depreciated linearly over 50 years; that is, the book value of the building decreases at a constant rate, so that at the end of 50 years the book value is zero.
The yearly depreciation will be
1,000,000/50=20,000 dollars.
Using this depreciation, the book value of the office building in dollars for different years can be calculated as follows:
Book value of the office building in 2013 can be calculated as,
16 x 20,000 = 320,000.
Book value of the office building in 2017 can be calculated as,
20 x 20,000 = 400,000.
Book value of the office building in 2025 can be calculated as,
28 x 20,000 = 560,000
.Thus, the book value of the office building in 2013 is $320,000; the book value of the office building in 2017 is $400,000, and the book value of the office building in 2025 is $560,000.
To know more about book value visit:
https://brainly.com/question/32128743
#SPJ11
Select the correct answer. What is 42% of 75? A. 315 B. 105 C. 31.5 D. 10.5
Answers
1% = 0,01
42% = 42 * 0,01 = 0,42
42% of 75 = 0,42 * 75 = 31,5
Answer: C)
Alligator 1 initial weight is 4 lbs. the rate of growth is 2 lbs. per month. Alligator 2 initial weight is 8 lbs. the rate of growth is 1 lb per month. After how many months will both alligators weigh the same amount?
Answers
Answer:
4 monthsStep-by-step explanation:
Let the number of months be x
Alligator 1 weight = 4 + 2x
Alligator 2 weight = 8 + x
4 + 2x = 8 + x2x - x = 8 - 4x = 4The answer is 4 months
You need a 25% alcohol solution. On hand; you have a 225 mL of a 20% alcohot mixture. You also haver 70 sh alcohol mixture. How much of the 70% mixture will you nered to add to obtain the desired solution? You wilt need mL. of the 70% solution
Answers
25 ml alcohol will need to add to obtain desired solution.
To obtain a 25% alcohol solution, we need to calculate the amount of a 70% alcohol mixture that should be added to a given 20% alcohol mixture.
We have 225 mL of the 20% mixture available and the amount of the 70% mixture needed will be calculated.
Let's assume the amount of the 70% alcohol mixture needed is x mL. To calculate the amount, we can set up an equation based on the alcohol content in the mixture. The total amount of alcohol in the resulting mixture should be equal to the sum of the alcohol in the 20% mixture and the alcohol in the 70% mixture.
The equation can be written as:
\(0.20*225*+0.70*x=0.25*(225+x)\)
Simplifying the equation will allow us to solve for x, which represents the amount of the 70% alcohol mixture needed to obtain the desired 25% solution.
To solve the equation 0.20 * 225 + 0.70 * x = 0.25 * (225 + x), we can follow these steps:
Distribute the 0.25 on the right side of the equation:
0.20 * 225 + 0.70 * x = 0.25 * 225 + 0.25 * x
Multiply the values:
45 + 0.70 * x = 56.25 + 0.25 * x
Rearrange the equation to isolate the x term on one side:
0.70 * x - 0.25 * x = 56.25 - 45
Simplify:
0.45 * x = 11.25
Divide both sides of the equation by 0.45 to solve for x:
x = 11.25 / 0.45
Calculate:
x ≈ 25
Therefore, the solution to the equation is x ≈ 25.
To learn more about equation click here:
brainly.com/question/29657983
#SPJ11
Which of the following equations have infinitely many solutions?
Choose all answers that apply:
A
- 10x - 10 = -10x + 10
B
10x - 10 = -10x - 10
C
- 10x - 10 = -10x - 10
D
10x – 10 = -10x + 10
Answers
Answer:
10
Step-by-step explanation:
that is the answer because its her choice
How do you calculate cubic meter volume?
Answers
Cubic meters are calculated by multiplying the length, width, and height of a space.
1. Measure the length of the space in meters.
2. Measure the width of the space in meters.
3. Measure the height of the space in meters.
4. Multiply the length, width, and height of the space together.
5. The result is the volume in cubic meters.
For example, if a room is 6 meters long, 5 meters wide, and 3 meters high, the volume would be calculated by multiplying 6 x 5 x 3, which equals 90 cubic meters.
Cubic meters measure the volume of a space, and can be calculated by multiplying the length, width, and height of a space. To calculate the cubic meter volume, first measure the length of the space in meters. Then measure the width of the space in meters. Next, measure the height of the space in meters. Finally, multiply the length, width, and height of the space together to get the volume in cubic meters. For example, if a room is 6 meters long, 5 meters wide, and 3 meters high, the volume would be calculated by multiplying 6 x 5 x 3, which equals 90 cubic meters. Cubic meters are a useful tool for determining the capacity of a space, and can be used for a variety of calculations, such as estimating the amount of materials required for construction projects.
Learn more about Cubic meters here
https://brainly.com/question/4771864
#SPJ4
This one is hard can some body help me

Answers
Please Help Me I Don’t Understand

Answers
For a complete triangle to form it needs to be 180°. So all you do is subtract 180° by the sum of 32° and 81°.
180°-113°=67°
The answer is 67°
Convert 150 grains to milligrams
Answers
Answer:
9179.84
Step-by-step explanation:
150 grams to milligrams is 9179.84
How do you use the distributive property to rewrite and evaluate 15(2 1/3)?
Answers
The value of the equation after the evaluation is 35
The operation on numbers that are available in brackets can be distributed for each number outside the bracket, according to the distributive property. It is one of the mathematical properties that is used the most. Commutative and associative qualities are the other two important features.
The distributive property is straightforward to recall. Numerous mathematical features allow us to make algebraic expressions as well as arithmetic calculations simpler.
Using the distributive property we can rewrite this expression as:
\(15(2\frac{1}{3} )= (15*2)+(15*\frac{1}{3} )\)→\(30\)→\(\frac{15}{3}\)→\(30+5\)→\(35\)
Evaluating the equation:
\(15(2\frac{1}{3} )=15*(\frac{7}{3} )=35\)
To learn more about the distributive property visit: brainly.com/question/5637942
#SPJ4
give the appropriate form of the partial fraction decomposition for the following function 4x/(x-7)^2(x^2 2)
Answers
The appropriate form of the partial fraction decomposition for the function 4x/((x-7)^2(x^2 + 2)) is A/(x-7) + B/(x-7)^2 + (Cx + D)/(x^2 + 2).
To find the appropriate form of the partial fraction decomposition for the function 4x/((x-7)^2(x^2 + 2)), we follow a systematic approach. First, we factorize the denominator to identify the distinct linear and irreducible quadratic factors:
Denominator: (x-7)^2(x^2 + 2)
The denominator consists of two linear factors: (x-7) and (x^2 + 2). Since the quadratic factor, x^2 + 2, cannot be factored further over real numbers, we treat it as an irreducible quadratic.
Now, we proceed to the partial fraction decomposition by assuming the numerator of the original function as:
4x = A/(x-7) + B/(x-7)^2 + (Cx + D)/(x^2 + 2)
To determine the unknown coefficients A, B, C, and D, we perform the common denominator operation:
4x = A(x-7)(x^2 + 2) + B(x^2 + 2) + (Cx + D)(x-7)^2
Next, we simplify this equation by expanding and collecting like terms:
4x = A(x^3 - 5x^2 - 14x + 14) + B(x^2 + 2) + (Cx^3 - 7Cx^2 - 14Cx + Dx^2 - 14Dx + 49C - 49D)
Now, we group the terms with the same powers of x:
4x = (A + C)x^3 + (-5A - 7C + D)x^2 + (-14A - 14C - 14D)x + (14A + 2B + 49C - 49D)
By comparing the coefficients of x^3, x^2, x, and the constant term on both sides of the equation, we can form a system of equations to solve for the unknown coefficients A, B, C, and D.
The resulting system of equations is:
A + C = 0 (coefficients of x^3)
-5A - 7C + D = 0 (coefficients of x^2)
-14A - 14C - 14D = 4 (coefficients of x)
14A + 2B + 49C - 49D = 0 (constant term)
By solving this system of equations, you can find the appropriate values for A, B, C, and D, which will complete the partial fraction decomposition of the given function.
Learn more about decomposition here
https://brainly.com/question/30763777
#SPJ11
what is the expression in factored form 4x^2+11x+6
Answers
Answer:
4x² + 11x + 6 = (x + 2)(4x + 3)
Help!!!!
Describe the transformation from the graph of f(x) = x to the graph of g(x) = 3/4x
Answers
A function f(x) is vertically compressed by a factor of 3/4 to form a function g(x)
In this question, we have been given two functions f(x) = x and g(x) = 3/4x
We need to describe the transformation from the graph of f(x) = x to the graph of g(x) = 3/4x
Here, the parent function is f(x) = x
and the transformed function is g(x) = 3/4x
That is, the parent function was multiplied by 3/4, which means that it was vertically compressed by a factor of 3/4, as when a function f(x) is multiplied by a value of a such that |a| < 1, it is vertically compressed by a factor of a.
Therefore, function f(x) is vertically compressed by a factor of 3/4 to form a function g(x)
Learn more about the transformation here:
brainly.com/question/16965753
#SPJ1
I knew y= 2x + 1 was a positive slope because...
Answers
Answer:
because the coefficient is positive
Step-by-step explanation:
hope it helps
This extreme value problem has a solution with both a maximum value and a minimum value. Use Lagrange multipliers to find the extreme values of the function subject to the given constraint. f(x, y) = x2 − y2; x2 + y2 = 9
Answers
The maximum value of the function is 9, and the minimum value of the function is −9.
We have function is f(x,y)=x²−y² and constraint is x²+y²=9,
For getting the extreme values of the function subject to the given constraint using Lagrange multipliers
Firstly we will form the Lagrangian function L (x,y,λ) as follows:
L (x,y,λ)=f(x,y)+λ(g(x,y))
Where f(x,y) = x²−y²and g(x,y) = x²+y² = 9
Thus, L (x,y,λ) = x²−y² + λ(x²+y² = 9)
Now we have to find the partial derivatives of L (x,y,λ) with respect to x,y and λ and equate them to 0 for finding the critical points.
\(L_x= 2x+2 \lambda x = 0\) .......(1)
\(L_y= -2y+2 \lambda y = 0\) ........(2)
\(L_{\lambda}= x^2+y^2-9 = 0\) (3)
From the above equations (1) and (2),we get
2x+2λx = 0 ⇒ x(1+λ) = 0
Thus, x = 0 and λ = -1
Similarly, y = 0 and λ = 1
From equations (1) and (2), we have
2λx = -2x ⇒ λ = -1
Therefore, x = 0 is not acceptable
From equations (1) and (2), we have
2λy = 2y ⇒ λ = 1
Therefore, y = 0 is not acceptable
Now using equation (3),we have
x²+y²-9 = 0
⇒ x²+0-9 = 0
⇒ x = ±3
Substituting x = 3 in equation (1), we get λ = -1
Hence, the first solution is (x,y) = (3,0)
Similarly, substituting x = -3 in equation (1), we get λ = -1
Hence, the second solution is (x,y) = (-3,0)
Now we will classify the obtained critical points as maxima or minima or saddle points
For finding the nature of critical points, we will form a Hessian matrix H of second partial derivatives of the Lagrangian function L at the critical point (x,y) as follows:
\($$ H = \left[\begin{array}{ccc} L_{xx}&L_{xy}\\L_{yx}&L_{yy}\\\end{array}\right] \\\)
On evaluating the Hessian matrix H at the critical point (x,y) = (3,0), we get the Hessian matrix as
\($$ H =\left[\begin{array}{ccc}4&0\\0&-2\\\end{array}\right]\)
Here, the determinant of the Hessian matrix,
\($$ D(H) = \left[\begin{array}{ccc} L_{xx}&L_{xy}\\L_{yx}&L_{yy}\\\end{array}\right] \\\)
= (4)(-2)-(0)(0)
= -8 < 0
Hence, Hessian matrix H is negative definite at the critical point (3,0)
Therefore, the function has a local maximum at (3,0)
On evaluating the Hessian matrix H at the critical point (x,y) = (-3,0), we get Hessian matrix as
\($$ H =\left[\begin{array}{ccc}4&0\\0&-2\\\end{array}\right]\)
Here, the determinant of the Hessian matrix,
\($$ D(H) = \left[\begin{array}{ccc} L_{xx}&L_{xy}\\L_{yx}&L_{yy}\\\end{array}\right] \\\)
= (4)(-2)-(0)(0)
= -8 < 0
Hence, Hessian matrix H is negative definite at the critical point (-3,0)Therefore, the function has a local maximum at (-3,0)Hence, the extreme values of the function are as follows:
The maximum value of the function f(x,y) = x² - y², subject to the given constraint x²+ y² = 9, is 9 at (3,0) and (-3,0)
Hence, the solution is -9.
To know more about the "Lagrange multipliers": https://brainly.com/question/4609414
#SPJ11
I will give brainlist! I promise!
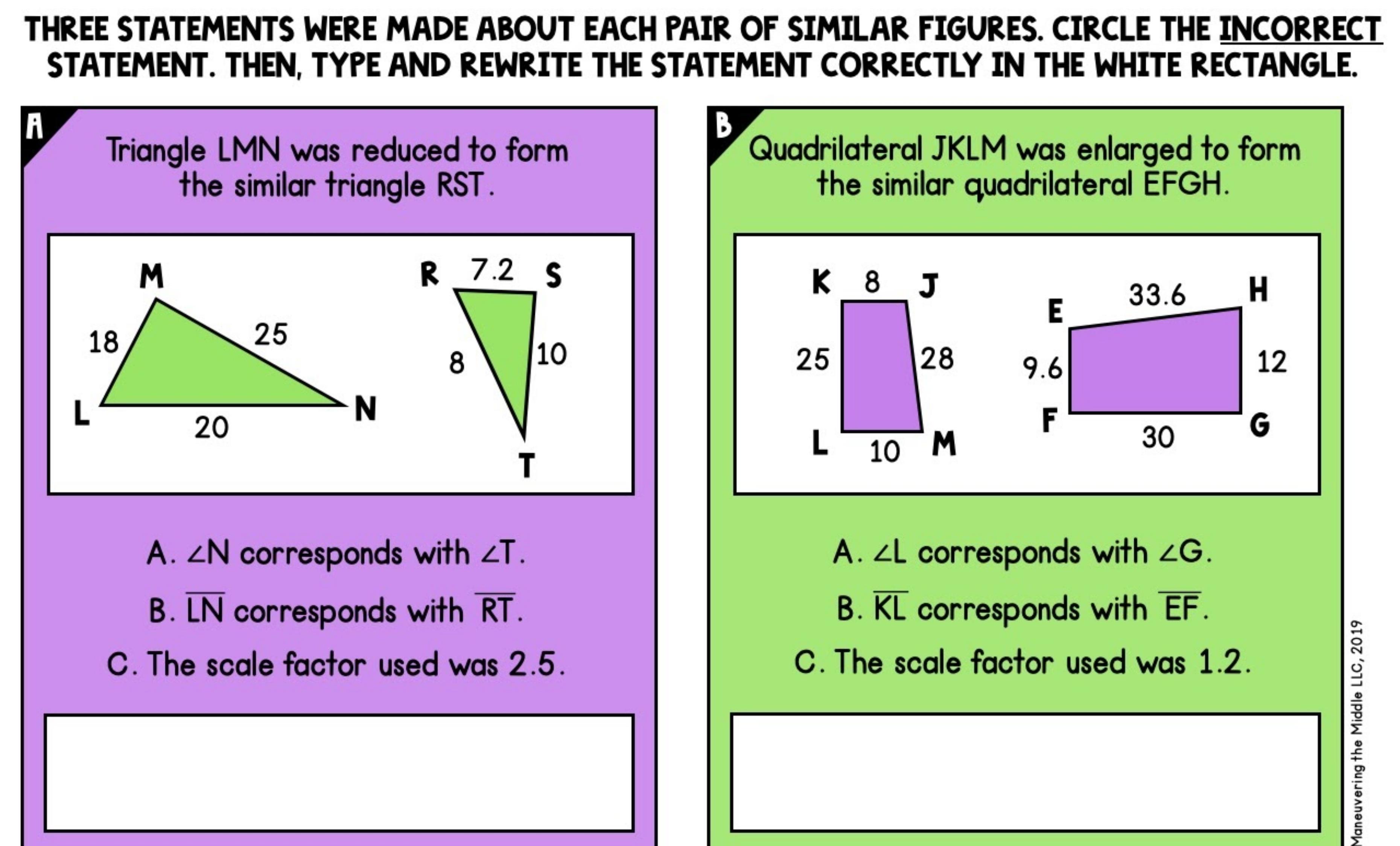

Answers
Answer:
Picture A: statement c is incorrect. It should be: The scale factor used was 0.4.
Picture B: statement B is incorrect. It should be: Line KL corresponds with line FG.
Second pic:
Amos was correct
Tash was correct
Both were correct
Step-by-step explanation:
HELP ME PLEASEEEEEEE

Answers
Answer:
x = 6
Step-by-step explanation:
Using the exterior angle theorem
The exterior angle of a triangle is equal to the sum of the 2 opposite interior angles.
79° is an exterior angle of the triangle , then
8x - 13 + 9x - 10 = 79
17x - 23 = 79 ( add 23 to both sides )
17x = 102 ( divide both sides by 17 )
x = 6
in a shooting match, eight clay targets are arranged in two hanging columns of three targets each and one column of two targets. a marksman is to break all the targets according to the following rules: 1) the marksman first chooses a column from which a target is to be broken. 2) the marksman must then break the lowest remaining target in the chosen column. if the rules are followed, in how many dierent orders can the eight targets be broken?
Answers
Therefore, there are 72 different orders in which the eight targets can be broken according to the given rules.
To find the number of different orders in which the eight targets can be broken, we can consider the arrangement of the columns and the targets within each column. Since there are three targets in each of the first two columns and two targets in the third column, we can focus on the relative order of breaking the targets within each column. Let's represent the columns as follows:
Column 1: T T T
Column 2: T T T
Column 3: T T
To calculate the number of different orders, we can count the permutations of breaking the targets within each column and then multiply them together.
For Column 1, there are 3 targets, so there are 3! = 3 × 2 × 1 = 6 possible orders.
For Column 2, there are also 3 targets, so there are 3! = 6 possible orders.
For Column 3, there are 2 targets, so there are 2! = 2 possible orders.
To find the total number of different orders, we multiply the number of orders for each column:
Total number of orders = 6 × 6 × 2
= 72
To know more about orders,
https://brainly.com/question/31859840
#SPJ11
An exam consists of 40 multiple-choice questions. Each question has a choice of five answers, only one of which is correct. For each correct answer, a candidate gets 1 mark, and no penalty is applied for getting an incorrect answer. A particular candidate answers each question purely by guess-work. Using Normal approximation to Binomial distribution with continuity correction, what is the estimated probability this student obtains a score greater than or equal to 10? Please use R to obtain probabilities and keep at least 6 decimal places in intermediate steps.
A. 0.7234 B. 0.2766 C. 0.5927 D. 0.1615 E. 0.3773
Answers
The estimated probability that the candidate obtains a score greater than or equal to 10 is 0.7234, rounded to four decimal places, so the answer is (A).
The number of correct answers that the candidate gets is a binomial random variable with parameters n = 40 (number of trials) and p = 1/5 (probability of success). We want to find the probability that the candidate gets a score greater than or equal to 10, which is equivalent to getting 10 or more questions correct.
Using the normal approximation to the binomial distribution with continuity correction, we can approximate the distribution of the number of correct answers by a normal distribution with mean μ = np = 40 * 1/5 = 8 and variance σ^2 = np(1-p) = 40 * 1/5 * 4/5 = 6.4.
To find the probability that the candidate gets 10 or more questions correct, we can standardize the normal distribution and use the standard normal distribution table or R to find the probability.
Let X be the number of correct answers. Then, we have:
P(X >= 10) = P((X - μ) / σ >= (10 - μ) / σ)
= P(Z >= (10 - 8) / sqrt(6.4)), where Z is a standard normal random variable.
For more similar questions on probability:
brainly.com/question/13604758
#SPJ11
Which equation shows y=3x−15 in standard form?
15x+y=-1
15x-5=1
5x-15y=1
5x-15y=-1
Answers
Answer:
the correct answer would be I think 5x-15y=1
Step-by-step explanation:
I have already learned that
Answer:
it's 5x - 15y = 1
Step-by-step explanation:
Hope this helped have a wonderful day!!! :)
Find the Mean given Normal Curve Values (please help and explain your answer)

Answers
Answer:
mean = 22
Step-by-step explanation:
34 = mean + 2sd
4 = mean - 3sd ==> mean = 4 + 3sd
34 = 4 + 3sd + 2sd
30 = 5sd
sd = 6
mean = 4 + 3*6 = 4 + 18 = 22
6x-3=5x-5
can someone help me
Answers
Answer:
x=-2
Step-by-step explanation:
To find the value of x you will have to isolate the x.
6x-3=5x-5 ------> Add 3 to both sides to get rid of the 3
6x=5x-2 ------> Subtract 5x to both sides to get rid of the 5x
1x=-2
1x is the same as x so
x=-2
How many paths are there from $A$ to $B,$ if you travel along the edges? You can travel along each edge at most once, but you can pass through the same point more than once. (You can pass through $B,$ as long as you end up at the point $B.$) [asy] unitsize(1.5 cm); draw((0,0)--dir(60)--(1,0)); draw((0,0)--(1,0)); draw((0,0)--dir(-60)--(1,0)); label("$A$", (0,0), W); label("$B$", (1,0), E); [/asy]
Answers
Answer:
There are $\boxed{3}$ paths from $A$ to $B.$
a trade magazine routinely checks the drive through service times of fast food restaurants. a 90% confidence interval that results from examining 653 customers in one fast food chains drive through has a lower bound of 178.2 secinds and an upper bound of 181.6 seconds. what does this mean?
Answers
The 90% confidence interval obtained from examining 653 customers in one fast food chain's drive-through has a lower bound of 178.2 seconds and an upper bound of 181.6 seconds. This means that based on the sample data collected from the 653 customers, we can be 90% confident that the true average drive-through service time for this fast food chain falls within the range of 178.2 seconds to 181.6 seconds.
In other words, if we were to repeatedly sample 653 customers from the same fast food chain's drive-through and calculate confidence intervals, approximately 90% of those intervals would contain the true average service time of the entire population of customers.
The range between the lower and upper bounds of the confidence interval provides an estimate of the precision or uncertainty associated with our sample mean.
The narrower the interval, the more precise our estimate of the true population mean becomes. In this case, the interval is relatively narrow, indicating a relatively precise estimate of the average drive-through service time for this fast food chain based on the sample data.
To know more about confidence interval refer here:
https://brainly.com/question/32278466#
#SPJ11
Select the correct answer from each drop-down menu.
onsider this equation.
-1-5 = I-8
The equation has
and
A valid solution for x is
Answers
The equation √(x – 1) – 5 = x – 8 has the solution 2 and 5. But the valid solution for x will be 5.
The complete question is attached below.
What is the solution of the equation?The solution of the equation means the value of the unknown or variable.
The equation is given below.
√(x – 1) – 5 = x – 8
Add 5 on both sides, then we have
√(x – 1) = x – 3
Square on both sides, then
x – 1 = (x – 3)²
x – 1 = x² – 6x + 9
x² – 7x + 10 = 0
Then the factor of the equation will be
x² – 7x + 10 = 0
x² – 5x – 2x + 10 = 0
(x – 5)(x – 2) = 0
x = 5, 2
Then the valid solution will be 5.
More about the solution of the equation link is given below.
https://brainly.com/question/545403
#SPJ1

pls help Pls no links

Answers
Hey there!
3^15/ 3^3
3^15
= 3*3*3*3*3*3*3*3*3*3*3*3*3*3*3
= 9*9*9*9*9*9*9*3
= 81*81*81*27
= 6,561 * 2,187
= 14,348,907
= 14,348,907/3^3
3^3
= 3*3*3
= 9*3
= 27
14,348,907/27
= 531,441
15 - 3 = 12
= 3^12
Because
3^12
= 3*3*3*3*3*3*3*3*3*3*3*3
= 9*9*9*9*9*9
= 81*81*81
= 6,561*81
= 531,441
531,441 ≈ 3^12
Therefore, your answer should be: 3^12
Good luck on your assignment and enjoy your day!
~Amphitrite1040:)
Hello! Guys I need some you to help me to solve this Areas of triangles homework. Shown down below. can you also give me the equation to solve it aswell.
I also need help on theses trapezium area questions can you give me the equation.
thanks!
( Do Not Delete This Question, Anybody!)**




Answers
Answer:
sorry I didn't this answer
Answer:
see explanation
Step-by-step explanation:
The area (A) of a triangle is calculated as
A = \(\frac{1}{2}\) bh ( b is the base and h the perpendicular height )
(1)
b = 6 and h = 9 , then
A = \(\frac{1}{2}\) × 6 × 9 = 3 × 9 = 27 cm²
(2)
b = 3 and h = 5 , then
A = ×\(\frac{1}{2}\) × 3 × 5 = 1.5 × 5 = 7.5 cm²
(3)
b = 6 and h = 10 , then
A = \(\frac{1}{2}\) × 6 × 10 = 3 × 10 = 30 cm²
(4)
b = 8 and h = 14 , then
A = \(\frac{1}{2}\) × 8 × 14 = 4 × 14 = 56 cm²
(5)
b = 7 and h = 9 , then
A = \(\frac{1}{2}\) × 7 × 9 = 3.5 × 9 = 31.5 cm²
--------------------------------------------------------------------
The figures are composed of a rectangle and a triangle
The area is the sum of the areas of the rectangle and the triangle
A = (5 × 4) + \(\frac{1}{2}\) × 5 × 4
= 20 + 10
= 30 cm²
(2)
A = (7 × 5) + \(\frac{1}{2}\) × 7 × 2
= 35 + 7
= 42 cm²
--------------------------------------------------------------------
The area (A) of a trapezium is calculated as
A = \(\frac{1}{2}\) h (a + b)
where h is the perpendicular height and a, b the parallel bases
(1)
A = \(\frac{1}{2}\) × 5 × (7 + 11) = 2.5 × 18 = 45 cm²
(2)
A = \(\frac{1}{2}\) × 6 × (6.6 + 8.4) = 3 × 15 = 45 cm²
(3)
A = \(\frac{1}{2}\) × 4.3 × (9.1 + 7.1) = 2.15 × 16.2 = 34.83 cm²
------------------------------------------------------------------------
The figure consists of a rectangle in the middle and 2 trapezium at the ends
A = \(\frac{1}{2}\) × 6 × (10 + 12) + (12 × 15) + \(\frac{1}{2}\) × 11 × (12 + 9)
= 3 × 22 + 180 + 5.5 × 21
= 66 + 180 + 115.5
= 361.5 m²
Divide by 20 to find number of cans required
361.5 ÷ 20 = 18.075
Only whole tins can be bought , so 19 tins required
cost = 19 × £6 = £114
Pentru o petrecere s-au folosit 1243 baloane albe,cu 7559 mai multe baloane galbene, albastre cu 1138 mai multe decat albe,iar rosii cat galbene si albastre la un loc.cate baloane s-au folosit in total
Answers
To find the total number of balloons used, we need to add the quantities of white, yellow, blue, and red balloons together.
Let's break down the given information:
- The number of white balloons used is 1243.
- There are 7559 more yellow balloons than white balloons.
- The number of blue balloons is 1138 more than the number of white balloons.
- The number of red balloons is equal to the combined quantity of yellow and blue balloons.
First, let's determine the number of yellow balloons. Since there are 7559 more yellow balloons than white balloons, we add 7559 to the quantity of white balloons:
1243 + 7559 = 8802 yellow balloons.
Next, let's determine the number of blue balloons. As there are 1138 more blue balloons than white balloons, we add 1138 to the quantity of white balloons:
1243 + 1138 = 2381 blue balloons.
Now, let's calculate the number of red balloons. The number of red balloons is equal to the sum of yellow and blue balloons:
8802 + 2381 = 11183 red balloons.
Finally, to find the total number of balloons used, we add the quantities of white, yellow, blue, and red balloons:
1243 + 8802 + 2381 + 11183 = 23609 balloons in total.
In total, 23609 balloons were used for the party. For the party, a total of 23609 balloons were used. The breakdown of balloon colors is as follows: 1243 white balloons, 8802 yellow balloons, 2381 blue balloons, and 11183 red balloons. To arrive at these numbers, we followed the given information step by step. First, we determined the quantity of yellow balloons by adding 7559 (the number of yellow balloons that exceeded the white balloons) to the initial quantity of white balloons (1243). This gave us a total of 8802 yellow balloons. Then, we calculated the quantity of blue balloons by adding 1138 (the number of blue balloons that exceeded the white balloons) to the initial quantity of white balloons (1243). This resulted in 2381 blue balloons. Finally, we found the quantity of red balloons by adding the number of yellow balloons (8802) and the number of blue balloons (2381), resulting in 11183 red balloons. Adding up the quantities of white, yellow, blue, and red balloons, we obtained a total of 23609 balloons for the party.
In conclusion, the total number of balloons used for the party was 23609, consisting of 1243 white balloons, 8802 yellow balloons, 2381 blue balloons, and 11183 red balloons.
To learn more about initial quantity visit:
brainly.com/question/1578659
#SPJ11