Entered Answer Preview Result -[tan(7*t)] - (tan(7t)) correct 7*([sec(7*t)]^2) 7 sec (7t) incorrect At least one of the answers above is NOT correct. (1 point) Given x = sin 7t and y cos 7t, find the following derivatives as functions of t dy/dx = -tan(7) dºg/d2 = 7sec^(2) 7t)
Answers
derivatives as functions dy/dx = -tan(7t)
d²y/dx² = -7sec^2(7t)
Given x = sin(7t) and y = cos(7t), we need to find dy/dx and d²y/dx².
First, let's find dy/dx:
dy/dx = (dy/dt) / (dx/dt)
Taking the derivatives:
dx/dt = 7cos(7t)
dy/dt = -7sin(7t)
Now we can find dy/dx:
dy/dx = (dy/dt) / (dx/dt) = (-7sin(7t)) / (7cos(7t)) = -tan(7t)
Next, let's find d²y/dx²:
d(dy/dx)/dt = d(-tan(7t))/dt
Taking the derivative:
d(dy/dx)/dt = -7sec^2(7t)
Learn more about derivatives here :-
https://brainly.com/question/29144258
#SPJ11
Related Questions
John is entering retirement on a decreased income. at his retirement party, he was gifted a small amount of money that he'd like to invest. in the coming years, he wants to see a positive return on his investment but cannot afford to lose it. which is the best investment choice for john? (2 points)
us treasury bond
common stock
preferred stock
corporate bond
Answers
US Treasury bond is the best investment choice for John in his retirement.
What investment option provides a positive return without risking loss for John's retirement?In order to secure a positive return without jeopardizing his investment, John should consider investing in a US Treasury bond.
As he enters retirement with a decreased income, it is crucial for him to prioritize capital preservation and minimize the risk of losing his investment.
US Treasury bonds are backed by the US government and are regarded as low-risk investments.
They offer a fixed interest rate and are considered safer compared to other options such as common stocks or corporate bonds, which involve a higher level of risk.
Preferred stocks, while relatively less risky than common stocks, may not provide the stability and security that John requires during his retirement.
Therefore, opting for a US Treasury bond aligns with his investment goals and risk tolerance.
Learn more about US Treasury bonds
brainly.com/question/30837260
#SPJ11
Graph the function
4-X, for x 2
1 - 3x for x>2
OA.
OB.
10
10-
n
x
ETT
ZAH
LILLE
LIETTE
- 10
10
Answers
magsagot ka kasi wagpuro brainly
Whahahaha
Slope = 2; y-intercept = -1
Answers
Answer: y=2x-1
Step-by-step explanation:
In slope intercept form y=Mx+b
Mx=slope and b=intercept
Y=2x-1
The equation of line with slope m = 2 and y-intercept is -1 is given by
y = 2x - 1
What is an Equation of a line?The equation of a line is expressed as y = mx + b where m is the slope and b is the y-intercept
And y - y₁ = m ( x - x₁ )
y = y-coordinate of second point
y₁ = y-coordinate of point one
m = slope
x = x-coordinate of second point
x₁ = x-coordinate of point one
The slope m = ( y₂ - y₁ ) / ( x₂ - x₁ )
Given data ,
Let the equation of line be represented as A
Now , the value of A is
Let the slope of the line m = 2
Let the y intercept of the line b = -1
Now , equation of a line is expressed as y = mx + b where m is the slope and b is the y-intercept
Substituting the values in the equation , we get
y = 2x - 1 be equation (1)
Therefore , the value of A is y = 2x - 1
Hence , the equation of line is y = 2x - 1
To learn more about equation of line click :
https://brainly.com/question/14200719
#SPJ5
Determine which is the better investment: 3.38% compounded semiannually or 3.51% compounded quarterly. Round your answers to 2 decimal places.
The 3.38% semiannual investment gives an effective rate of ____ %.
The 3.51% quarterly investment gives an effective rate of ____ %.
Therefore, the _______ investment is a better investment.
Answers
The 3.51% compounded quarterly investment is the better investment in terms of higher returns.
We need to compare the effective rates of return for both options in order to determine which investment is superior.
A) For the 3.38% accumulated semiannually, we can work out the successful rate utilizing the equation:
The effective rate is as follows: Effective Rate = (1 + (Annual Interest Rate / Number of Compounding Periods)) Number of Compounding Periods - 1 Annual Interest Rate = 3.38 percent Number of Compounding Periods = 2 (since it is compounded semiannually) Effective Rate = (1 + (0.0338 / 2)) 2 - 1
The 3.38% compounded semiannual investment has an effective rate of approximately 3.59%, which is calculated as follows: Effective Rate = (1 + 0.0169)2 - 1 Effective Rate 0.0359385 or 3.59% (rounded to two decimal places).
B) We can use the same formula to determine the effective rate for the quarterly compound interest rate of 3.51 percent:
Since it is compounded quarterly, there are four compounding periods, and the annual interest rate is 3.51 percent. The effective rate is equal to (1 + (0.0351 / 4))4 - 1.
The compounded quarterly investment at 3.51% has an effective rate of approximately 3.53%, which is calculated as follows: Effective Rate = (1 + 0.008775)4 - 1 Effective Rate 0.0353157 or 3.53% (rounded to two decimal places).
When we look at the effective rates, we can see that the compounded quarterly investment with a rate of 3.51 percent has a slightly higher effective rate (3.53%) than the compounded semiannual investment with a rate of 3.38 percent (3.59%). Consequently, the higher-return investment at 3.51 percent compounded quarterly is superior.
To know more about Investment, visit
brainly.com/question/24703884
#SPJ11
Perimeter of a Square What is the maximum perimeter of a square that can fit inside a circle of radius 5 cm?
A. 20
B. 20 â2
C. 10/ â12
D. 40
E. 20/ â12
Answers
The answer to this question is none of the given options (A, B, C, D, or E).To find the maximum perimeter of a square that can fit inside a circle of radius 5 cm, we need to consider that the diameter of the circle is equal to the diagonal of the square.
This means that the side of the square will be equal to the radius of the circle multiplied by the square root of 2 (since the diagonal of a square is the side length times the square root of 2).
So, the side length of the square will be 5 cm x √2 = 7.07 cm. And since a square has four sides of equal length, the perimeter of the square will be 4 x 7.07 cm = 28.28 cm.
However, this perimeter is greater than the circumference of the circle with radius 5 cm, which is 2 x π x 5 cm = 31.42 cm. This means that the square cannot fit entirely inside the circle.
Therefore, the answer to this question is none of the given options (A, B, C, D, or E).
learn more about diagonal here: brainly.com/question/9752237
#SPJ11
Can somebody help me with this?

Answers
R = (-6, 7) ➡️ R’ = (6, -7)
S = ( -3, 5) ➡️ S’ = (3, -5)
T = ( -2, 0) ➡️ T’ = ( 2, 0)
U = ( -8, 4) ➡️ U’ = (8, -4)
Step by step
The rule for a rotation by 180° is (x,y)→(−x,−y)
So we plot the pre image coordinates, then we change the sign on our x and y coordinates and re-plot them on the graph
What is the solution set for this system of equations?
4x + y = -12
x − 5y = -3
help, please
Answers
Answer:
x = -3
y = 0
Step-by-step explanation:
4x + y = -12
x − 5y = -3
Times the second equation by -4
4x + y = -12
-4x + 20y = 12
21y = 0
y = 0
Now put 0 back in for y and solve for x
4x + 0 = -12
4x = -12
x = -3
Let's check
4(-3) + 0 = -12
-12 + 0 = -12
-12 = -12
So, x = -3 and y = 0 is the correct answer.
Answer:
(-3,0)
x = -3
y = 0
Step-by-step explanation:
4x + y = -12
x − 5y = -3
Enter the second equation by -4
4x + y = -12
-4x + 20y = 12
21y = 0
y = 0
Now enter 0 for y
4x + 0 = -12
4x = -12
x = -3
Plug that info in
4(-3) + 0 = -12
-12 + 0 = -12
-12 = -12
Therefore x = -3 and y = 0
a chili recipe calls for ground beef, beans, green pepper, onion, chili powder, crushed tomatoes, salt, and pepper. you have lost the directions about the order in which to add the ingredients, so you decide to add them in a random order. what is the probability that the first ingredient you add is either ground beef or onion?
Answers
The probability of adding either ground beef or onion as the first ingredient 0.25 or 25%.
If there are a total of 8 ingredients and 2 of them are either ground beef or onion, then the probability would be:
Probability = (Number of desired outcomes) / (Total number of possible outcomes)
= 2 / 8
= 1 / 4
= 0.25
So, the probability of adding either ground beef or onion as the first ingredient is 0.25 or 25%.
In this case, we have a total of 8 ingredients, out of which 2 are either ground beef or onion. When selecting the first ingredient, there are 8 possible outcomes. Since we want to calculate the probability of adding either ground beef or onion as the first ingredient, we count the number of desired outcomes, which is 2 (either ground beef or onion). Dividing the number of desired outcomes by the total number of possible outcomes gives us the probability.
The probability of adding either ground beef or onion as the first ingredient is 0.25 or 25%. This means that there is a 25% chance that either ground beef or onion will be the first ingredient added, assuming the ingredients are added randomly without any specific order.
To know more about probability follow the link:
https://brainly.com/question/24756209
#SPJ11
Sean started cycling at time A.
He stopped cycling at time B.
Sean cycled for a total of Hours and Minutes?

Answers
Sean cycled for a total of One hour and five minutes.
Sean started cycling at time A. From the image, the hour hand is between 2 and 3, and the minute hand points to 8. So, time A is 2 O' clock 40 minutes.
He stopped cycling at time B. From the image, the hour hand is between 3 and 4, and the minute hand points to 9. So, time B is 3 O' clock 45 minutes.
The time he spent cycling can be determined by finding the difference between time B and A.
Time = 3 O' clock 45 minutes - 2 O' clock 40 minutes.
= 1 hour 5 minutes.
Hence, Sean cycled for a total of 1 hour and 5 minutes.
To read about a similar problem on clocks click https://brainly.com/question/24051741
Find 3 ratios that are equivalent to the given ratio.
Question content area bottom
Part 1
Find three ratios that are equivalent to the given ratio.
16:36
Answers
Two ratios are equivalent if they have the same value. Therefore, 16:36 is equivalent to 2:4, 8:18, and 4:9 since all three have the same value of 0.4444 when expressed as a decimal or 4/9 when expressed as a fraction.
A ratio is a mathematical expression that compares two values. It is expressed as a fraction in the form of a:b, where a and b are the two values being compared. The ratio 16:36 is equivalent to 2:4, 8:18, and 4:9.The ratio 16:36 can be expressed as a fraction as 16/36. This fraction can be simplified by dividing both the numerator and denominator by 4, resulting in 4/9.Since every ratio can be expressed as a fraction, it can also be expressed as a decimal. A decimal is a way of representing a fraction in a base ten system. To convert the fraction 16/36 to a decimal, divide 16 by 36. This result is 0.4444, which can be expressed as 4/9.Finally, two ratios are equivalent if they have the same value. Therefore, 16:36 is equivalent to 2:4, 8:18, and 4:9 since all three have the same value of 0.4444 when expressed as a decimal or 4/9 when expressed as a fraction.Finally, we can use the concept of equivalent fractions to find another equivalent ratio. Since 16:36 is a fraction, we can find an equivalent fraction by multiplying both terms by the same number. For example, if we multiply both terms by 3, our new ratio is 48:108, which is equivalent to 16:36. In summary, three equivalent ratios to 16:36 are 4:9, 32:18, and 48:108.1. 16:36 = 8:18
Divide each side by 8:
16/8 = 2
36/8 = 4.5
Ratio = 2:4.5
2. 16:36 = 4:9
Divide each side by 4:
16/4 = 4
36/4 = 9
Ratio = 4:9
3. 16:36 = 2:4.5
Divide each side by 2:
16/2 = 8
36/2 = 18
Ratio = 8:18
Learn more about ratio here:
https://brainly.com/question/29467965
#SPJ1
using complete sentences, explain which function has the greatest y-intercept.

Answers
Answer:
Step-by-step explanation:
To determine which function has the greatest y-intercept, we need to look at the constant term, which represents the y-intercept, of each function. The function with the largest constant term will have the greatest y-intercept.
For example, consider the following three functions:
1. f(x) = 2x + 5
2. g(x) = 3x - 7
3. h(x) = -4x + 10
The constant term for each function is 5, -7, and 10 respectively. Therefore, h(x) has the greatest y-intercept of 10, since its constant term is larger than those of f(x) and g(x).
A bus traveled on a straight road for 3 h at an average speed that was 12 mph faster than its average speed on a winding road. The time spent on the winding road was 3 h. Find the average speed on the winding road if the total trip was 210 mi.
Answers
The average speed on the winding road was 45 mph.
The bus traveled for 3 hours on the winding road, so the distance covered can be calculated using the formula: Distance = Speed × Time. Let's assume the average speed on the winding road as 'x' mph. Therefore, the distance covered on the winding road is 3x miles.
On the straight road, the bus traveled for 3 hours at an average speed that was 12 mph faster than its average speed on the winding road. So the average speed on the straight road can be expressed as 'x + 12' mph. The distance covered on the straight road can be calculated as 3(x + 12) miles.
The total distance covered in the entire trip is given as 210 miles. Therefore, we can write the equation:
3x + 3(x + 12) = 210
Simplifying the equation:
3x + 3x + 36 = 210
6x + 36 = 210
6x = 174
x = 29
So the average speed on the winding road was 29 mph.
The problem states that the bus traveled for 3 hours on both the winding road and the straight road. Let's assume the average speed on the winding road as 'x' mph. Since the bus traveled for 3 hours on the winding road, the distance covered can be calculated as 3x miles.
On the straight road, the average speed was 12 mph faster than on the winding road. Therefore, the average speed on the straight road can be expressed as 'x + 12' mph. The distance covered on the straight road can be calculated as 3(x + 12) miles.
The total distance covered in the entire trip is given as 210 miles. This allows us to set up the equation 3x + 3(x + 12) = 210 to solve for 'x'. Simplifying the equation leads to 6x + 36 = 210. Solving for 'x', we find that the average speed on the winding road was 29 mph.
In summary, the average speed on the winding road was 29 mph.
Learn more about distance
brainly.com/question/13034462
#SPJ11
the period of a simple pendulum is 1 s on earth. when brought to a planet where g is one-tenth that on earth, its period becomes
a.√10 s
b.10 s
c.1/10 s
d.1/√10 s
Answers
The period of a simple pendulum is 1 s on Earth. when brought to a planet where g is one-tenth that on earth, its period becomes (d) 1/√10 s.
The period of a simple pendulum is given by the equation T = 2π√(L/g), where T is the period, L is the length of the pendulum, and g is the acceleration due to gravity.
On Earth, the period is 1 s, which means that 1 = 2π√(L/gEarth).
When the same pendulum is taken to a planet where g is one-tenth that on Earth, the equation becomes T = 2π√(L/(g/10)).
We want to find the new period, so we can solve for T: T = 2π√(L/(g/10)) = 2π√(10L/g).
We know that the length of the pendulum does not change, so we can substitute L from the first equation into the second equation: T = 2π√(10/gEarth).
We can simplify this equation by dividing the numerator and denominator of the square root by gEarth:
T = 2π√(10/gEarth) * (√gEarth/√gEarth) = 2π√(10gEarth/gEarth^2) = 2π√(10/9.81) s.
Therefore, the answer is (d) 1/√10 s.
Know more about pendulum here:
https://brainly.com/question/26449711
#SPJ11
The measure of angle Y is 45°, and the measure of angle Z is 70°.
A triangle has angles X, Y, Z. The exterior angle to angle X is W.
What is the measure of angle W?
25°
65°
115°
120°
Answers
Answer:
115
Step-by-step explanation:
ON EDGE.2020
Answer:
115°
Step-by-step explanation:
Please answer the following if 5x4 is 20 what is 9x2?
Answers
Step-by-step explanation:
well, 5×4 IS 20.
I am not sure, what your teacher wants here.
and therefore, as a fact, 9×2 = 18.
maybe it is to show the fraction relationship between the teens of the first operation and the terms of the second.
9 = 5×9/5
2 = 4×2/4
so, 9×2 = 9/5 × 2/4 × 20 = 18/20 × 20 = 18
I consider this nonsense, but it is the only thing I can currently think of to do with these operations in relation to each other.
two draws are made at random without replacement from a box containing the following five tickets: golden ticket with a one printed on it. golden ticket with a two printed on it. golden ticket with a three printed on it. golden ticket with a 4 printed on it. golden ticket with a three printed on it. what is the probability that the sum of the tickets is 5? enter you answer as a percentage. the probability is
Answers
The probability to draw tickets with a sum of 5 is 30%.
According to the question, there are 5 tickets with 1, 2, and 4 printed on one ticket each, while there are 2 tickets with the number 3 printed on them.
We need to find the probability of drawing 2 tickets with a sum of 5 out.
Probability = no of possibilities for an event/total no. of possibilities
From these 5 tickets, 2 tickets at random can be drawn in
⁵C₂ ways.
= 5 X 4
= 20 ways.
Now the possible combinations to draw a sum of 5 is
(1,4) , (2,3) , (2,3) , (3,2) , (3,2) , (4,1)
= 6 ways
Here there are 2 tickets with 3 printed on them so events concerning 3 will be repeated in the sample space.
Hence, the probability to draw 2 tickets with a sum of 5 is
6/20
= 3/10
= 30%
To learn more about probability visit
https://brainly.com/question/29251004
#SPJ4
Rick found the are of this shape is 15 square unit. If he used a smaller unit square, would his measurement be greater than 15 squares units or less than 15 square units?
Answers
Answer:
greater
Step-by-step explanation:
this is true because it is like going from feet to inches 1ft=12in the number gets larger
pls help will give brainiest !!!! pls hurry pls pls

Answers
Answer:
"D" (2,4), (-2,-4)
Step-by-step explanation:

How do you simplify algebraic expressions?
Answers
Answer:
remove parentheses by multiplying factors.
use exponent rules to remove parentheses in terms with exponents.
combine like terms by adding coefficients.
combine the constants.
Step-by-step explanation:
If Ø lies in the quadrant IV what can be the value of cos Ø
Answers
\(▪▪▪▪▪▪▪▪▪▪▪▪▪ {\huge\mathfrak{Answer}}▪▪▪▪▪▪▪▪▪▪▪▪▪▪\)
The values of Cos Ø is always positive in the Quadrant IV.
X/6 = 3 x=____ help
Answers
Answer:
x =18
Step-by-step explanation:
\(\frac{x}{6} = 3\)
x = 3 x 6
x = 18
Verify:
\(\frac{18}{6} =3\) (Correct)
(07.04 MC)
Given the expression: 4x¹0-64x²
Part A: Rewrite the expression by factoring out the greatest common factor. (4 points)
Part B: Factor the entire expression completely. Show the steps of your work. (6 points)
STEPS PLEASE
Answers
Answer:
Part A: The greatest common factor of 4x¹0 and 64x² is 4x². Factoring it out gives:4x²( x¹0 - 16)
Therefore, the expression 4x¹0-64x² can be rewritten as 4x²(x¹0 - 16) by factoring out the greatest common factor.
Part B: To factor 4x¹0-64x² completely, we can first factor out the greatest common factor of 4x², which gives:4x²(x^8 - 16)
Then, we can use the difference of squares formula to factor x^8 - 16, which gives:
4x²(x^4 + 4)(x^2 + 2)(x^2 - 2)
Therefore, the fully factored form of 4x¹0-64x² is 4x²(x^4 + 4)(x^2 + 2)(x^2 - 2).
PLEASE HELP ASAP PLEASE CORRECT

Answers
Answer: C,A,D
Step-by-step explanation:
IMAGE IS DOWN BELOW!!
SOMEONE PLEASE HELP ME!!
ILL GIVE YOU BRAINLIST ANSWER AND POINTS!!

Answers
Answer:
14.3
Step-by-step explanation:
Formula: a^2 + b^2 = c^2
9+196= 205 then find the square root of 205, approximate then use tenths.
Answer:
14.3
Step-by-step explanation:
Use the following equation:
a² + b² = c² , in which the variable c = hypotenuse, and a & b are the other legs.
It is given that the legs measure 3 and 14 respectively. Plug in the given numbers to the given leg variables:
a² + b² = c²
3² + 14² = c²
Simplify. First, solve the powers, and then combine like terms:
(3 * 3) + (14 * 14) = c²
9 + 196 = c²
c² = 205
Next, root both sides of the equation:
√c² = √205
c = √205 = 14.3178
c = 14.3 (Rounded to the nearest tenth).
14.3 is your answer.
~
Use the exchange rate £1 = $1.35 to convert $54 into £.
Answers
Answer:
£40
Step-by-step explanation:
If £1 = $1.35
To convert $ to £, divide $ by 1.35
⇒ $54 = 54/1.35 = £40
how deep would a water container have to be to have the same pressure at the bottom as that found at the bottom of a 10.0 -cm deep beaker of mercury, which is 13.55 times as dense as water
Answers
A 10 cm deep beaker mercury will have the same hydrostatic pressure as 133.5 cm deep water.
The hydrostatic pressure exerted by a fluid is given by:
P = ρ.g.h
Where:
ρ = fluid density
g = gravitational acceleration
h = fluid depth
We want to compare 2 types of fluid, water and mercury.
Divide both sides of the equation by h
P/h = ρ.g
Since pressure is held constant, then the fluid density is inversely proportional to the fluid depth.
Therefore,
h_water : h_mercury = ρ_mercury : ρ_water
Given that:
ρ_mercury = 13.55 ρ_water and h_mercury = 10 cm
Then,
h_water : 10 = 13.55 ρ_water : ρ_water
h_water : 10 = 13.55 : 1
h_water = 13.55 × 10 = 135.5 cm
Learn more about hydrostatic pressure here:
https://brainly.com/question/11758621
#SPJ4
if (1,-7) is in the solution area of the inequality y ≤ 1x + b, what is the smallest value of b possible?
Answers
Check your solution by first checking the end point , in the related equation. Pick a value greater than , such as 2, to check in the inequality. Solve for x. Divide both sides by 3 to isolate the variable.
helppp please this is homework you will be marked as brainlest

Answers
Answer:
Step-by-step explanation:

Which lines are parallel? Check all that apply.
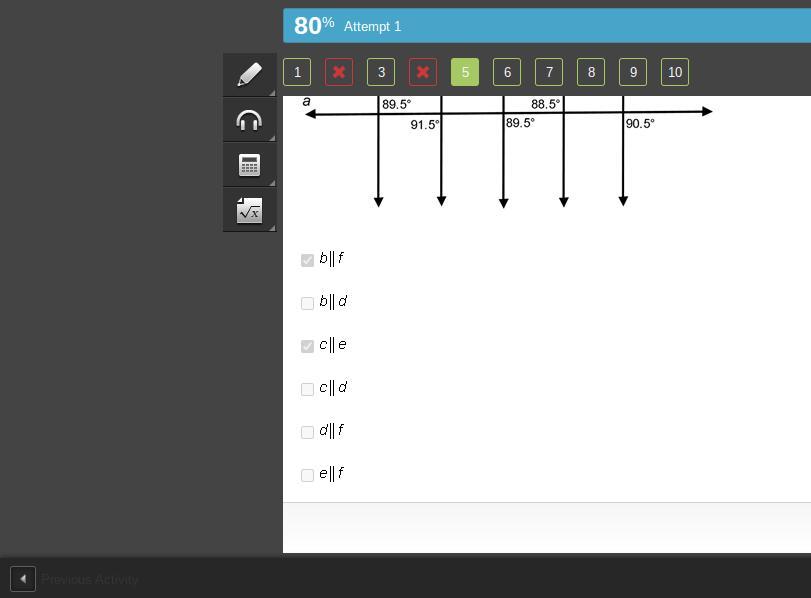
Lines b, c, d, e, f are cut by transversal a. Clockwise from top left, the angles formed by lines b and a are blank, 89.5 degrees, blank, blank; by lines c and a are blank, blank, blank, 91.5 degrees; by lines d and a are blank, blank, 89.5 degrees, blank; by lines e and a are 88.5 degrees, blank, blank, blank; by lines f and a are blank, blank, 90.5 degrees, blank.
b is parallel to f
b is parallel to d
c is parallel to e
c is parallel to d
d is parallel to f
e is parallel to f

Answers
Answer:
I think it's A and C
b║f
c║e
(I'm so sorry if it's wrong)
Hope this Helps!
Answer:
A and c are correct because i just took the test
Step-by-step explanation:
please help me if you can. please show how you got the answer.

Answers
Answer:
Step-by-step explanation:
The area of a circle is A = πr², where r is the radius. That means in order to solve this we have to find the value of x, which is the diameter of the lake, and then divide it in half to get the radius. To find x we will use similar triangles and proportions. x is the height of the big triangle and 4.5 is the height of the smaller triangle; 15.3 + 7.4 is the hypotenuse of the big triangle and 7.4 is the hypotenuse of the smaller triangle. Setting up our proportion:
\(\frac{x}{4.5}=\frac{15.3+7.4}{7.4}\) which simplifies a bit to
\(\frac{x}{4.5}=\frac{22.7}{7.4}\) and cross multiply to solve for x:
7.4x = 102.15 so
x = 13.8 That is the diameter of the lake. Divide it in half to get 6.9, the radius. Applying the area formula for a circle:
A = (3.14)(6.9)² and
A = 3.14(47.61) so
A = 149.5 which rounds to 150, Choice C