find the HCF of 18(2x^3-x^2-x)and 20(24x^4 +3x)
Answers
The HCF of 18(2x³ - x² - x) and 20(24x⁴ + 3x) is 6x³.
To find the HCF of 18(2x³ - x² - x) and 20(24x⁴ + 3x),
we need to factor both expressions.
Let's factor the first expression by using the distributive property.
18(2x³ - x² - x) = 2(9x³ - 4.5x² - 2x²)
The HCF of the first expression is 2x².20(24x⁴ + 3x) = 20(3x)(8x³ + 1)
The HCF of the second expression is 3x.The HCF of both expressions is the product of their
HCFs.
HCF = 2x² × 3xHCF = 6x³
For more question HCF
https://brainly.com/question/31308898
#SPJ8
Related Questions
. f(x) = Square root of quantity x plus eight. ; g(x) = 8x - 12 Find f(g(x)). (1 point) f(g(x)) = 2 Square root of quantity two x plus one. f(g(x)) = 8 Square root of quantity x plus eight. - 12 f(g(x)) = 2 Square root of quantity two x minus one. f(g(x)) = 8 Square root of quantity two x plus one.
Answers
Answer:
\(f(g(x))\) = \(\sqrt{8x - 4}\)
Step-by-step explanation:
• \(f(x) = \sqrt{x + 8}\)
• \(g(x) = 8x - 12\)
\(f(g(x))\) is the combination of the functions \(f(x)\) and \(g(x)\) such that \(g(x)\) is the input to the function \(f(x)\) .
This means, we have to replace the original input of \(f(x)\), which is \(x\), with the function \(g(x)\).
∴ \(f(g(x))\) = \(f(8x - 12)\)
⇒ \(\sqrt{8x - 12 + 8}\)
⇒ \(\sqrt{8x - 4}\)
7. Giovanni made the design below for an art project. What is the area of the drawing? 13 in. 5 in. 4in.

Answers
Answer:
75 in^2
Step-by-step explanation:
Given data
From the figure
We can see a rectangle and a triangle
The area of the rectangle is
Area= L*W
Area= 13*5
Area= 65 in^2
Area of the triangle
Area= 1/2b*h
Area= 1/2*4*5
Area= 2*5
Area= 10 in^2
Hence the area of the composite figure is
Area= 65+10
Area= 75 in^2
Are these two lines perpendicular?
Line 1: y-1=3(x+7)
Line 2: y-19=-1/2(x+1)
Answers
Answer:
Step-by-step explanation:
This is the image of the graph you determine if that's perpendicular.
Perpendicular definition - In elementary geometry, the property of being perpendicular is the relationship between two lines which meet at a right angle. The property extends to other related geometric objects. A line is said to be perpendicular to another line if the two lines intersect at a right angle.

4x-5=x-1+3x I need help
Answers
Answer:
x = no solutions
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
Brackets Parenthesis Exponents Multiplication Division Addition Subtraction Left to RightEquality Properties
Step-by-step explanation:
Step 1: Define equation
4x - 5 = x - 1 + 3x
Step 2: Solve for x
Combine like terms: 4x - 5 = 4x - 1Subtract 4x on both sides: -5 ≠ -1Here we see that -5 does not equal -1.
∴ This equation has no solutions.
A lake was closed because of an accidental pesticide spill. The concentration of the pesticide after the spill was 848 parts per million. Each day the water is tested, and the amount of pesticide is found to be about 75% of what was there the day before. Do you think the lake will ever be completely free of the pesticide? Explain.
Answers
Answer:
Step-by-step explanation:
\(a_{n}=a_{1}r^{n-1}\\0=848(0.75)^{n-1}\\or~(0.75)^{n-1}=0\\0.75<1\\so~(0.75)^{n-1} \rightarrow 0,if~n-1 \rightarrow ~\infty\)
\(or~n \rightarrow 1+\infty\\or~n \rightarrow \infty\)
Hence lake will never be free of pesticide.
Simplify the expression:
-3(3-4x) =
Answers
Answer:
- 9 + 12x
Step-by-step explanation:
- 3(3 - 4x) ← multiply each term in the parenthesis by - 3
= - 9 + 12x
Factor 16a+72 to identify the equivalent expressions. choose 2 answers a.4(4a+18) b.8(2a+9) c.2(8+36a) d.2(8a+72)
help ASAP
Answers
Answer:
\( \boxed{\sf b. \ 8(2a + 9)} \)
Step-by-step explanation:
\( \sf Factor \: the \: following: \\ \sf \implies 16a + 72 \\ \\ \sf Factor \: 8 \: out \: of \: 16a + 72: \\ \sf \implies 8 \times 2a + 8 \times 9 \\ \\ \sf \implies 8(2a + 9)\)
mathematical procedures used to assume or understand predictions about the whole population, based on the data collected from a random sample selected fom the population, are called
Answers
The answer of the given question is inferential statistics.
The mathematical procedures used to assume or understand predictions about the whole population, based on the data collected from a random sample selected from the population, are called inferential statistics.
To know more about Population visit:
https://brainly.com/question/16894337
#SPJ11
The mathematical procedures used to assume or understand predictions about the whole population based on data collected from a random sample selected from the population are called statistical inference techniques.
Statistical inference involves drawing conclusions, making predictions, and testing hypotheses about population parameters based on sample data. These techniques include methods such as estimation, hypothesis testing, confidence intervals, and regression analysis.
By using statistical inference, we can generalize findings from the sample to make inferences about the larger population, allowing us to make informed decisions and draw meaningful conclusions based on the available data.
To know more about Population related question visit:
https://brainly.com/question/15889243
#SPJ11
Find the exact value of tan 0.

Answers
Answer:
B
Step-by-step explanation:
please help quick im so confused

Answers
Answer:
(-5/2,-4)
Step-by-step explanation:
the answer is (x, y) = (-5/2, -4)
One month before an election, a poll of 630 randomly selected voters showed 55% planning to vote for a certain candidate. A week later it became known that he had had an extramarital affair, and a new poll showed only 53% of 1010 voters supporting him. Do these results indicate a decrease in voter support for his candidacy?
Determine the test statistic. z= (Round to two decimal places as needed.)
Find the P-value.
estimate that difference, p1−p2, with a 95% confidence interval
Answers
The statistics are as follows:
- Test Statistic: The calculated test statistic is approximately 1.02.
- P-value: The P-value associated with the test statistic of 1.02 is approximately 0.154.
- Confidence Interval: The 95% confidence interval for the difference in proportions is approximately -0.0186 to 0.0786.
To solve the problem completely, let's go through each step in detail:
1. Test Statistic:
The test statistic can be calculated using the formula:
z = (p1 - p2) / √[(p_cap1 * (1 - p-cap1) / n1) + (p_cap2 * (1 - p_cap2) / n2)]
We have:
p1 = 0.55 (proportion in the first poll)
p2 = 0.53 (proportion in the second poll)
n1 = 630 (sample size of the first poll)
n2 = 1010 (sample size of the second poll)
Substituting these values into the formula, we get:
z = (0.55 - 0.53) / √[(0.55 * (1 - 0.55) / 630) + (0.53 * (1 - 0.53) / 1010)]
z = 0.02 / √[(0.55 * 0.45 / 630) + (0.53 * 0.47 / 1010)]
z ≈ 0.02 / √(0.0001386 + 0.0002493)
z ≈ 0.02 / √0.0003879
z ≈ 0.02 / 0.0197
z ≈ 1.02 (rounded to two decimal places)
Therefore, the test statistic is approximately 1.02.
2. P-value:
To find the P-value, we need to determine the probability of observing a test statistic as extreme as 1.02 or more extreme under the null hypothesis. We can consult a standard normal distribution table or use statistical software.
The P-value associated with a test statistic of 1.02 is approximately 0.154, which means there is a 15.4% chance of observing a difference in proportions as extreme as 1.02 or greater under the null hypothesis.
3. Confidence Interval:
To estimate the difference in proportions with a 95% confidence interval, we can use the formula:
(p1 - p2) ± z * √[(p_cap1 * (1 - p_cap1) / n1) + (p_cap2 * (1 - p_cap2) / n2)]
We have:
p1 = 0.55 (proportion in the first poll)
p2 = 0.53 (proportion in the second poll)
n1 = 630 (sample size of the first poll)
n2 = 1010 (sample size of the second poll)
z = 1.96 (for a 95% confidence interval)
Substituting these values into the formula, we get:
(0.55 - 0.53) ± 1.96 * √[(0.55 * (1 - 0.55) / 630) + (0.53 * (1 - 0.53) / 1010)]
0.02 ± 1.96 * √[(0.55 * 0.45 / 630) + (0.53 * 0.47 / 1010)]
0.02 ± 1.96 * √(0.0001386 + 0.0002493)
0.02 ± 1.96 * √0.0003879
0.02 ± 1.96 * 0.0197
0.02 ± 0.0386
The 95% confidence interval for the difference in proportions is approximately (0.02 - 0.0386) to (0.02 + 0.0386), which simplifies to (-0.0186 to 0.0786).
To know more about confidence intervals, refer here:
https://brainly.com/question/32546207#
#SPJ11
a bag contains 5 red balls and 6 green balls. if two balls are taken out successively, without replacement, what is the probability that green is picked on the first pick given that at least one red is chosen? g
Answers
The probability of picking a green ball on the first pick, given that at least one red is chosen, is 11/19.
The probability of picking a green ball on the first pick, given that at least one red is chosen, can be calculated by finding the total number of possible outcomes and then dividing by the number of outcomes that include at least one red ball. In this bag, there are 11 green balls and 5 red balls, for a total of 16 balls. Since two balls are taken out successively without replacement, the total number of outcomes is 16 choose 2, or 120. Of those, there are 10 outcomes that include at least one red ball, so the probability of picking a green ball on the first pick, given that at least one red is chosen, is 11/19. This can be calculated by dividing the number of outcomes that include at least one red ball (10) by the total number of outcomes (120).
Learn more about probability here
https://brainly.com/question/11234923
#SPJ4
please help its due in 5 minutes
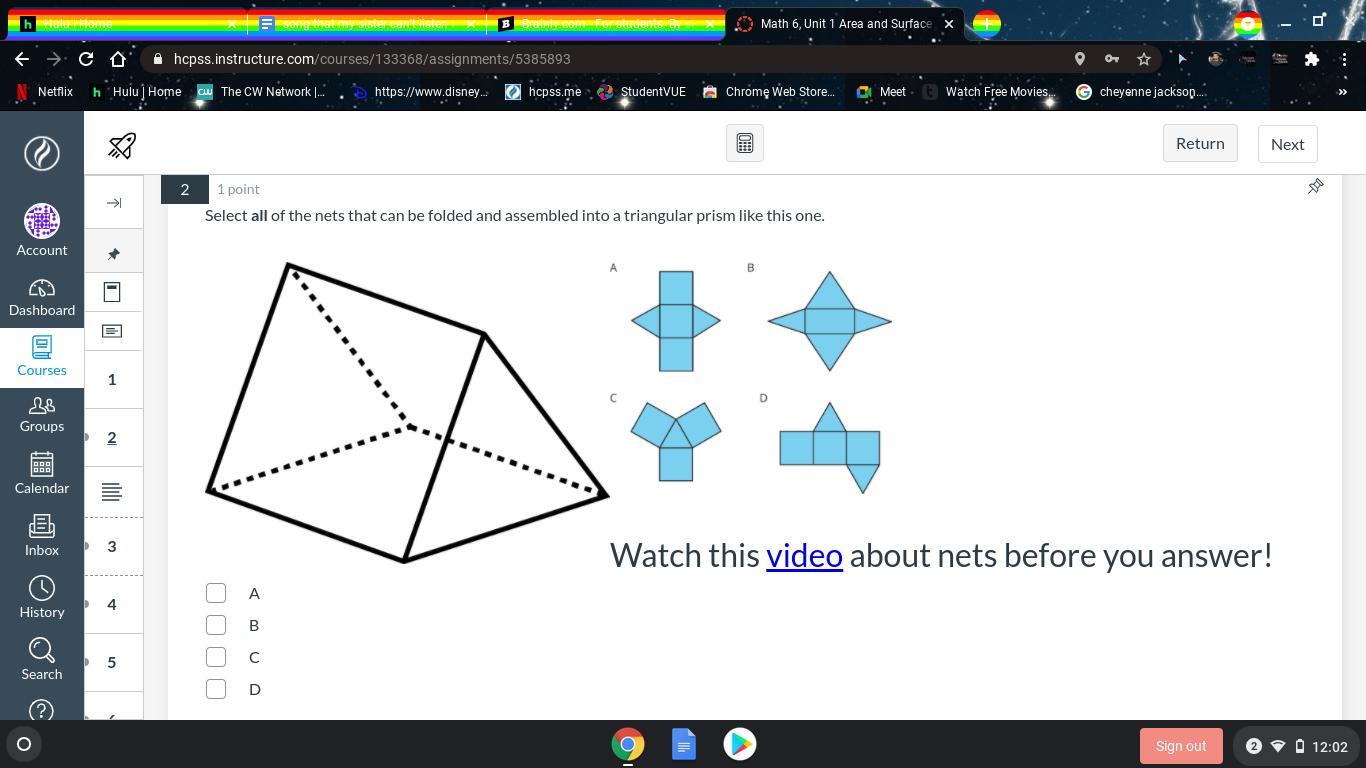
Answers
Answer: The answer is net B
Step-by-step explanation: If you look at the net it has one rectangle for the base and four triangles for the side. Then when you look at the completed figure the shapes are the same. Also all the other nets have the wrong shapes.
Hope this helps.
(Edit- was lookin at the wrong stuff answer = d lol sorry
Find the mode:
4,5, 4, 3, 5, 1, 6
Answers
Answer:
4 and 5Step-by-step explanation:
The mode in a given set of data is the number that appears the most.
4 appears twice
5 appears twice
3 appears once
1 appears once
6 appears once

Solve the system of equations.
y=x+2
y=4x+23
Write your answer as
X=
y=
Answers
Answer:
Step-by-step explanation:

The required solutions of the given system of equations is x = -7 and y = -5.
What are simultaneous linear equations?Simultaneous linear equations are two- or three-variable linear equations that can be solved together to arrive at a common solution.
Here,
Given system of equation
y=x+2 - - - - -(1)
y=4x+23 - - - - (2)
From above equations,
x + 2 = 4x + 23
x = -7
Now,
y = -7 + 2
y = -5
Thus, the required solutions of the given system of equations is x = -7 and y = -5.
Learn more about simultaneous equations here:
https://brainly.com/question/16763389
#SPJ5
Determined to the nearest 10th of a centimeter the arc length of a circle of radius 11.9 cm intercepted by an angle of 155°
I seriously am in need of desperate help considering I missed the day that this lesson was taught and I am very lost.
Answers
The arc length of the arc intercepted by an angle of 155° of a circle of radius 11.9 cm is 32.2 cm
What is arc length?The arc length is the portion of the circumference of a circle swept by radius by making some angle at the center. If this angle is measured in degrees say some α degrees, then the arc length is given by the formula:
Arc length = (α/360°)*(2πr) , where r is the radius of the circle
Given that a circle if of radius 11.9 cm and arc on its circumference is intercepted by an angle of 155° , r =11.9 and α = 155°
Then the arc length = (155°/360°)*(2π(11.9)) = (155*2*22*11.9)/(360*7)= 32.2 cm
Therefore, the arc length is 32.2
Also, Learn more about arc length from the below link:
https://brainly.com/question/16403495
#SPJ1
find the number of calories in a stalk of celery and in a carrot, a carrot hs 13 calories more then a celerystalk, five carrots and 1o celery stalks have only 170 calories
Answers
The number of calories in stalk of celerystalk and carrot is found as 20 and 7 respectively.
What is defined as the method of substitution?The algebraic method for solving simultaneous linear equations is the substitution method. The value with one variable through one equation is replaced in the other equation, as the name implies.For the given question;
Let the number of calories present in carrot is 'x'.
Let the number of calorie present in celerystalk is 'y'.
Carrot has 13 more calories than celerystalk.
Thus,
x = y + 13 ......eq 1
Now, 5 carrots and 10 celery stalks have total 170 calories.
The equation becomes.
5x + 10y = 170
Substitute the value of x from eq 1.
5(y + 13) + 10y = 170
Simplify the equation;
5y + 65 + 10y = 170
15y = 105
y = 7 (number of calories in stalk of celerystalk)
Put the value of y in eq 1.
x = y + 13
x = 7 + 13
x = 20 (number of calories in stalk of carrot)
Thus, the number of calories in stalk of celerystalk and carrot is found as 20 and 7 respectively.
To know more about the method of substitution, here
https://brainly.com/question/22340165
#SPJ9
Convert the point from rectangular coordinates to cylindrical coordinates and spherical coordinates. (-√3 ,3,−9).(a) cylindrical coordinates (r,θ,z)=( ) .(b) spherical coordinates (rho,θ,φ)=( )
Answers
(a) In cylindrical coordinates: (r, θ, z) = (3√2, -π/3, -9). (b) In spherical coordinates: (ρ, θ, φ) = (√91, -π/3, π/2).
(a) The point (-√3, 3, -9) in cylindrical coordinates is (r, θ, z) = (√(9 + 3), arctan(3/(-√3)), -9) = (3√2, -π/3, -9).
In cylindrical coordinates, the conversion from rectangular coordinates is done using the following formulas:
r = √(\(x^{2}\) + \(y^{2}\)),
θ = arctan(y/x),
z = z.
By substituting the given values (-√3, 3, -9) into the formulas, we obtain the cylindrical coordinates (r, θ, z) = (3√2, arctan(3/(-√3)), -9) = (3√2, -π/3, -9).
(b) The point (-√3, 3, -9) in spherical coordinates is (ρ, θ, φ) = (√(9 + 3 + 81), arctan(3/(-√3)), arccos(-9/√(9 + 3 + 81))) = (√91, -π/3, π/2).
In spherical coordinates, the conversion from rectangular coordinates is done using the following formulas:
ρ = √(\(x^{2}\) + \(y^{2}\) + \(z^{2}\)),
θ = arctan(y/x),
φ = arccos(z/√(\(x^{2}\) + \(y^{2}\) + \(z^{2}\))).
By substituting the given values (-√3, 3, -9) into the formulas, we obtain the spherical coordinates (ρ, θ, φ) = (√(9 + 3 + 81), arctan(3/(-√3)), arccos(-9/√(9 + 3 + 81))) = (√91, -π/3, π/2).
Learn more about cylindrical here:
https://brainly.com/question/30394340
#SPJ11
a bicyclist completes a 100-mile race in 3 hours and 45 minutes. what is the average speed in miles per hour?
Answers
3 hours and 45 minutes = 3.75 hours
\(\frac{100}{3.75}=\boxed{26.\overline{6}}\)

10 point help please!!!!!!!!!

Answers
Answer:
Side LM is congruent to side RQ
Angle MNO is congruent to angle RST
Side ON is congruent to side ST
Angle LMN is congruent to angle QRS
Step-by-step explanation:
A way to solve this is to use parchment paper or draw the same shape next to each other, as you will get these:
Side LM is congruent to side RQ
Angle MNO is congruent to angle RST
Side ON is congruent to side ST
Angle LMN is congruent to angle QRS
it takes 8 blocks with a side lengths of one fourths meter to fill a rectangular The rectangular prism has a volume of either one eights one fourths half or one
cubic meter.
Answers
The volume of the rectangular prism is 8 cubic meters when it takes 8 blocks with a side lengths of one fourths meter to fill a rectangular prism.
If it takes 8 blocks with a side length of one fourths meter to fill a rectangular prism, we can assume that the volume of each block is:
\((1/4)^3 = 1/64m^3\)
To find the volume of the rectangular prism, we need to know its dimensions. We can express its volume as one of the given options:
One eights cubic meters: This means the volume is 1/8 cubic meters. We can find the number of blocks needed to fill this volume by dividing the total volume by the volume of each block:
(1/8) ÷ (1/64) = 8 blocks
This doesn't match the given information, since we were told that it takes 8 blocks to fill the prism, not that the volume of the prism is 8 times the volume of a block.
One fourths cubic meters: This means the volume is 1/4 cubic meters. We can find the number of blocks needed to fill this volume in the same way:
(1/4) ÷ (1/64) = 16 blocks
This also doesn't match the given information.
Half cubic meters: This means the volume is 1/2 cubic meters. We can find the number of blocks needed to fill this volume:
(1/2) ÷ (1/64) = 32 blocks
Since it takes 8 blocks to fill the prism, this option doesn't match either.
One cubic meter: This means the volume is 1 cubic meter. We can find the number of blocks needed to fill this volume:
1 ÷ (1/64) = 64 blocks
This matches the given information, since it takes 8 blocks to fill the prism, which means there are 8 layers of 8 blocks each. Therefore, the dimensions of the prism are:
length = 8 × (1/4) = 2 meters
width = 8 × (1/4) = 2 meters
height = 8 × (1/4) = 2 meters
So the volume of the rectangular prism is:
volume = length × width × height = 2 × 2 × 2 = 8 cubic meters.
Learn more about rectangular prism :
https://brainly.com/question/21308574
#SPJ1
Town b is south 38 degree east from town y what is the bearing of town y from town b
Answers
The bearing is the angle measured clockwise from the north direction to a specified direction. To find the bearing of Town Y from Town B, we use the given information that Town B is located south 38 degrees east from Town Y. By subtracting this angle from 180 degrees, we find that the bearing is 142 degrees.
To determine the bearing, we need to find the angle between the north direction and the direction from Town B to Town Y.
Since Town B is located south of Town Y, the bearing will be a southern direction. The bearing angle can be calculated as 180 degrees minus the given angle, which is 38 degrees.
Therefore, the bearing of Town Y from Town B is 180 - 38 = 142 degrees.
In conclusion, the main answer is that the bearing of Town Y from Town B is 142 degrees.
Learn more about bearing:
https://brainly.com/question/24340249
#SPJ11
Assume that C(x) is in dollars and x is the number of units produced and sold. For the total-cost function C(x) 0.01x" +0.4x + 50, find ΔC and C'(x) when x-90 and ΔΧΖ 1.
Answers
When x = 90, ΔC = $5.31 and C'(x) = 2.2.
Given the total-cost function C(x) = 0.01x^2 + 0.4x + 50, we'll first find the change in cost (ΔC) and then the derivative of the cost function (C'(x)) when x = 90 and Δx = 1.
To find ΔC when x = 90 and ΔΧΖ = 1, we need to use the formula:
ΔC = C(x + ΔΧΖ) - C(x)
Substituting the values, we get:
ΔC = C(90 + 1) - C(90)
ΔC = C(91) - C(90)
ΔC = [0.01(91)^2 + 0.4(91) + 50] - [0.01(90)^2 + 0.4(90) + 50]
ΔC = 91.31 - 86
ΔC = $5.31
To find C'(x), we need to take the derivative of the total-cost function C(x):
C(x) = 0.01x^2 + 0.4x + 50
C'(x) = 0.02x + 0.4
Substituting x = 90, we get:
C'(90) = 0.02(90) + 0.4
C'(90) = 1.8 + 0.4
C'(90) = 2.2
Therefore, when x = 90, ΔC = $5.31 and C'(x) = 2.2.
Given the total-cost function C(x) = 0.01x^2 + 0.4x + 50, we'll first find the change in cost (ΔC) and then the derivative of the cost function (C'(x)) when x = 90 and Δx = 1.
1. To find ΔC, evaluate C(x + Δx) - C(x) when x = 90 and Δx = 1:
ΔC = C(90 + 1) - C(90) = C(91) - C(90)
2. Now, let's find the derivative of the cost function C(x):
C'(x) = d(0.01x^2 + 0.4x + 50)/dx = 0.02x + 0.4
3. Evaluate C'(x) when x = 90:
C'(90) = 0.02(90) + 0.4 = 1.8 + 0.4 = 2.2
So, ΔC = C(91) - C(90), and C'(x) when x = 90 is 2.2.
To know more about total-cost function visit:
https://brainly.com/question/29262808
#SPJ11
Lemma 1 Let g = (V, E, w) be a weighted, directed graph with designated root r e V. Let E' = {me(u): u E (V \ {r})}. Then, either T = (V, E') is an RDMST of g rooted at r or T contains a cycle. Lemma 2 Let g = (V, E, w) be a weighted, directed graph with designated root reV. Consider the weight function w': E → R+ defined as follows for each edge e = (u, v): w'le) = w(e) - m(u). Then, T = (V, E') is an RDMST of g = (V, E, W) rooted at r if and only if T is an RDMST of g = (V, E, w') rooted at r.
Answers
Lemma 1 states that in a weighted, directed graph with a designated root, if we create a new set of edges E' by removing edges from the root to each vertex except itself.
Lemma 1 introduces the concept of an RDMST (Rooted Directed Minimum Spanning Tree) in a weighted, directed graph and highlights the relationship between the set of edges E' and the existence of cycles in the resulting graph T. It states that if T is not an RDMST, it must contain a cycle, indicating that removing certain edges from the root to other vertices can lead to cycles.
Lemma 2 focuses on the weight function w' and its impact on determining an RDMST. It states that the resulting graph T is an RDMST rooted at the designated root in the original graph if and only if it is an RDMST rooted at the designated root in the graph with the modified weight function w'. This lemma demonstrates that adjusting the weights of the edges based on the weights of the vertices preserves the property of being an RDMST.
Overall, these two lemmas provide insights into the properties and characteristics of RDMSTs in weighted, directed graphs and offer a foundation for understanding their existence and construction.
Learn more about lemma here:
https://brainly.com/question/30759610
#SPJ11
HELP!!!!! How do you use properties of equality with fractions? For example, 1+r/9=4
Answers
The value of r in the equation is 35.
How to solve fractions?1 + r / 9 = 4
We have to find the value of r in the expression.
The value of r in the expression can be found by making r the subject of the formula.
Hence,
1 + r / 9 = 4
cross multiply
1 + r = 9 × 4
1 + r = 36
subtract 1 from both sides
1 - 1 + r = 36 - 1
r = 35
learn more on fractions here: brainly.com/question/12961756
#SPJ1
Please help i'm struggling with this help!

Answers
a beam having a circular cross-section of diameter, D, is designed to resist a maximum bending moment of 80kNm. the maximum allowable bending stress is 500MPa what is the minimum required diameter, D, of the cross section of the beam?
Answers
To determine the minimum required diameter (D) of the cross-section of the beam, we need to consider the maximum bending moment and the maximum allowable bending stress.
The bending stress in a beam is given by the formula:
σ = (M * c) / I
Where σ is the bending stress, M is the maximum bending moment, c is the distance from the neutral axis to the outermost fiber (which is equal to half of the diameter for a circular cross-section), and I is the moment of inertia of the cross-section.
Rearranging the formula, we have:
D = (2 * M) / (σ * π)
Substituting the given values, with M = 80 kNm (converted to Nm) and σ = 500 MPa (converted to N/m²), we can calculate the minimum required diameter (D):
D = (2 * 80,000 Nm) / (500,000,000 N/m² * π)
D ≈ 0.255 meters or 255 mm
Therefore, the minimum required diameter of the cross-section of the beam is approximately 0.255 meters or 255 mm to resist the maximum bending moment of 80 kNm within the allowable bending stress of 500 MPa.
To learn more about diameter click here:
brainly.com/question/31445584
#SPJ11
Sam is making a delivery to a store. The total trip will be 410 miles. He is driving at a constant rate of 65 miles per hour. He has already driven 20 miles. How much longer will it take him to get to the store?
Answers
Answer:
6 hours
Step-by-step explanation:
20 + 65x=410
65x=390
x=6
One option in a roulette game is to bet on the color red or black. (There are 18 red compartments, 18 black compartments and two compartments that are neither black nor red.) If you bet on a color you get to keep your bet and win that same amount if the color occurs. If that color does not occur you will lose the amount of money you wagered on that color to appear. What is the expected payback for this game if you bet $6 on red?
Answers
The expected payback for betting $6 on red in this roulette game is approximately -$0.32. This means, on average, you can expect to lose about $0.32 per $6 wagered.
To calculate the expected payback for the game, we need to consider the probabilities and payouts associated with the bet on red.
In a standard roulette wheel, there are 18 red compartments, 18 black compartments, and two green compartments (neither black nor red) representing the 0 and 00. This means there are 38 equally likely outcomes.
If you bet $6 on red, there are 18 favorable outcomes (the red compartments) and 20 unfavorable outcomes (the black and green compartments). Therefore, the probability of winning is 18/38, and the probability of losing is 20/38.
If the color red occurs, you get to keep your bet of $6 and win an additional $6.
To calculate the expected payback, we multiply the probability of winning by the payout for winning and subtract the probability of losing multiplied by the amount wagered:
Expected Payback = (Probability of Winning * Payout for Winning) - (Probability of Losing * Amount Wagered)
Expected Payback = ((18/38) * $6) - ((20/38) * $6)
Expected Payback = ($108/38) - ($120/38)
Expected Payback = -$12/38
The expected payback for betting $6 on red in this roulette game is approximately -$0.32. This means, on average, you can expect to lose about $0.32 per $6 wagered.
Visit to know more about Average:-
brainly.com/question/130657
#SPJ11
Find the volume of the largest rectangular box in the first octant with three faces in the coordinate planes, and one vertex in the plane.
Answers
The volume of the largest rectangular box in the first octant with three faces in the coordinate planes, and one vertex in the plane is V = xyz, where x, y, and z are the lengths of the sides of the rectangular box.
To find the largest volume, we need to maximize x, y, and z. Since we have three faces in the coordinate planes, one vertex will be at the origin (0, 0, 0). The other two vertices will lie on the coordinate axes.
Let's assume the vertex on the x-axis is (x, 0, 0), and the vertex on the y-axis is (0, y, 0). The third vertex on the z-axis will be (0, 0, z). Since the box is in the first octant, all the coordinates must be positive.
To maximize the volume, we need to find the maximum values for x, y, and z within the constraints. The maximum values occur when the box touches the coordinate planes. Therefore, the maximum values are x = y = z.
Substituting these values into the volume formula, we get V = xyz = x³. Therefore, the volume of the largest rectangular box is V = x³.
Learn more about constraints here
brainly.com/question/32387329
#SPJ11
What is the maximum volume of a rectangular box situated in the first octant, with three of its faces lying on the coordinate planes, and one of its vertices located in the plane?