Answers
The measure of ML is 8.69
What is Pythagoras theorem?Pythagoras theorem states that ;the sum of the squares on the legs of a right triangle is equal to the square on the hypotenuse.
Therefore, a²+b²= c²
Line JL is a diameter and it passes in through the center of the circle meeting a tangent JK. The angle formed between this lines is 90°. Therefore ∆JKL is a right angled triangle and Pythagoras theorem can be applied.
JL = √ 10.3²+ 14²
JL = √ 302.09
JL = 17.38
ML = JL/2
ML = 17.38/2
ML = 8.69
therefore the measure of ML is 8.69
learn more about Pythagoras theorem from
https://brainly.com/question/343682
#SPJ1
Related Questions
Drag the tiles to the correct boxes to complete the pairs. Not all tiles will be used.
Match the systems of equations to their solutions.

Answers
\(x = 2 \\ y = 7\)
is the answer to:
\(y = 11 - 2x \\ 4x - 3y = - 13\)
_________________________________________
\(x = 5 \\ y = 2\)
is the answer to:
\(2x + y = 12 \\ x = 9 - 2y\)
_________________________________________
\(x = 3 \\ y = 5\)
is the answer to:
\(2x + y = 11 \\ x - 2y = - 7\)
_________________________________________
\(x = 7 \\ y = 3\)
is the answer to:
\(x + 3y = 16 \\ 2x - y = 11\)
5-13 Question Help opping Two friends shop for fresh fruit. Elena buys a watermelon for $6.55 and 3 pounds of cherries niy buys a pineapple for $4.35 and 2 pounds of cherries. Use the variable p to represent the price, in lars, per pound of cherries. Write and simplify an expression to represent how much more Elena sper e expression represents how much more Elena spent than Taniy. mplify your answer. Use integers or decimals for any numbers in the expression.) nter your answer in the answer box and then click Check Answer. Clear All Check Ans I parts showing Review progress Question 6 of 12 Back Next →
Answers
Answer:
The expression;
\(2.2+p\)represents how much more Elena spent than Taniy
Explanation:
Let the variable p to represent the price per pound of cherries.
Given that Elena buys a watermelon for $6.55 and 3 pounds of cherries.
The total cost Elena spent is;
\(6.55+3p\)Taniy buys a pineapple for $4.35 and 2 pounds of cherries.
The total cost Taniy spent is;
\(4.35+2p\)The amount Elena spent more than Taniy is;
\(\begin{gathered} =(6.55+3p)-(4.35+2p) \\ =6.55-4.35+3p-2p \\ =2.2+p \end{gathered}\)Therefore, The expression;
\(2.2+p\)represents how much more Elena spent than Taniy
Parallelogram L M N O is shown. Angle L is (x + 40) degrees and angle O is (3 x) degrees. What is the measure of angle O in parallelogram LMNO? 35° 75° 105° 155
Answers
Answer:
C, 105 Degrees
Step-by-step explanation:
So the two opposite sides of a parallelogram is equal to each other and the two adjacent angles are supplementary. So if (x+40)+3x=180, this means that 4x+40=180. This gives us 4x=140, so x=35. If we plug it back into the equation it ascertains as such: 3(35)= 105. The answer for this question and angle O is 105 degrees, or C.
The measure of angle O in this parallelogram is 105°.
The properties of a parallelogramThe opposite angles of a parallelogram are equal.The Opposite sides of the parallelogram are equal and parallel.The diagonals of the parallelogram bisect each other.The Sum of the angles = 360°
Solution
Because the properties says that opposite angles are equal.
Angle L = (x + 40)
angle O = (3 x)
Applying the first property
x+40+x+40+3x+3x = 360
collect the like termsx+x+3x+3x+40+40 = 360
8x+80 = 360
8x = 360-80
8x = 280
Divide through the equation by 8
x = 280/8
x = 35
The question wants us to find the value of angle O
O = 3x
O = 3*35
= 105
The value of angle O is equal to 105°
Read more on parallelograms here:
https://brainly.com/question/970600
help me please 100 points please

Answers
Answer:
2(2W + W) = 60
Step-by-step explanation:
There are two lengths and two widths. The perimeter is the distance around the figure.
2(2w + w) = 60
4w + 2w = 60
6w = 60 Divide both sides by 6
w = 10
The width is 10. The length is twice as long 20
10 + 10+ 20 + 20 = 60
60= 60
Answer:
2(2W + W) = 60
Step-by-step explanation:
There are two lengths and two widths. The perimeter is the distance around the figure.
2(2w + w) = 60
4w + 2w = 60
6w = 60 Divide both sides by 6
w = 10
The width is 10. The length is twice as long 20
10 + 10+ 20 + 20 = 60
60= 60
Choose the correct reason to justify each of the first four statements in the derivation. 1) a2 = h2 x2
Answers
The Pythagorean Theorem could be represented mathematically as follows, Here, c represents the length of the hypotenuse (the longest side), or b or a are the lengths of the other 2 sides. From the equation, you can easily find the value of the 1 side if you have the values of the other 2
1) a2 = h2 + x2
Pythagorean theorem
2) h2 = a2 - x2
Rearrange the previous statement
3) c2 = h2 + (b-x)2
Pythagorean theorem
4) c2 = h2 + b2 -2bx + x2
Expand (b – x)2
What made Pythagoras think of the Pythagorean theorem?
The number 1 : the number of reason.
The number 2: the first even and female number, the number of opinion.
The number 3: the first true male number, the number of harmony.
The number 4: the number of justice or retribution.
The number 5: marriage.
The number 6: creation
Learn more about Pythagorean theorem here https://brainly.com/question/343682
#SPJ4
the following argument is valid: p1) if it is raining then then your car will get wet. p2) it is not raining. c) your car will not get wet.
Answers
Yes, the argument is valid. If the two premises (p1 and p2) are true, then the conclusion (c) must also be true.
The argument is valid because the conclusion is logically entailed by the two premises. If it is raining then the car will get wet, and if it is not raining then the car will not get wet. This follows from the logical law of noncontradiction, which states that for any statement, either it is true or its negation is true, but not both. Since the first premise states that it is raining, and the second premise states that it is not raining, the logical conclusion is that the car will not get wet.
The argument is based on a logical principle known as noncontradiction, which states that for any statement, either it is true or its negation is true, but not both. In this case, the two premises (p1 and p2) both concern the same statement: that it is raining. The first premise states that if it is raining then the car will get wet, and the second premise states that it is not raining. Therefore, the logical conclusion is that the car will not get wet. This conclusion follows logically from the two premises, so the argument is valid.
Learn more about premises here
https://brainly.com/question/29699382
#SPJ4
A stick is cut into three pieces, each having a different length. each piece (except the shortest) is twice as long as another piece. what fraction of the whole stick is each piece?
Answers
The fraction of the whole stick is each piece are 1/7, 2/7, and 4/7 respectively.
The given problem states that a stick is cut into three pieces, each having a different length.
Each piece (except the shortest) is twice as long as another piece.
We are to find the fraction of the whole stick is each piece.
Since we have three pieces of the stick, let us assume their lengths be a, b, and c respectively such that the length of the shortest stick is a.
As per the problem, each piece (except the shortest) is twice as long as another piece, thus their lengths can be taken as 2a and 4a respectively.
a + 2a + 4a = 7a
From the above equation, we can say that the sum of the lengths of the three pieces is 7a, which is equal to the length of the whole stick.
Hence, each of the three pieces has a fraction of the whole stick as follows:
a/7a = 1/7 (shortest piece)
2a/7a = 2/7 (middle piece)
4a/7a = 4/7 (longest piece)
Therefore, the fraction of the whole stick is each piece are 1/7, 2/7, and 4/7 respectively.
To learn more about fraction from the given link.
https://brainly.com/question/78672
#SPJ11
The volume of a cylinder is 100. Another cylinder has twice the height but half the base radius. What is the volume of the second cylinder
Answers
Answer:
50 units³Step-by-step explanation:
Cylinder volume formula:
V = πr²hGiven:
The first cylinder, has base radius - r and height - h. Its volume is:
V₁ = πr²h = 100The second cylinder has:
R = r/2 and H = 2hIts volume is:
V₂ = πR²H = π(r/2)²*(2h) = πr²h/2 = V₁/2Substitute the value of the first cylinder:
V₂ = V₁/2 = 100/2 = 50Darryl has a shipping box with dimensions 16 in. By 16 in. By 16 in. He needs a cube whose volume is three times bigger, to hold all his stuff. What will be the new dimensions rounded to the hundredths?
Answers
Answer:
23.08 in
Step-by-step explanation:
Volume of the shipping box = length × width × height
= 16 × 16 × 16
= 4,096 in³
He needs a cube whose volume is three times bigger
New volume of cube = 3 × 4,096 in
= 12,288 in
New volume of cube = 12,288 in³
New dimensions:
Volume of cube = s³
12,288 in³ = s³
s = 3√12,288
s = 23.0759931249 in
To the nearest hundredth = 23.08 in
2) The representative agent lives for infinite periods (0,1,2,…) and receives exogenous incomes of y0,y1,y2,…, respectively. The lifetime present discounted value of utility is given by: ∑t=0[infinity]βtln(ct) with β(<1) being the discount factor and ct is consumption at time t. The agent is allowed to save or borrow at the real interest rate r, but she cannot die with debt or wealth. Assume also that the initial wealth is zero. a. Solve the optimization problem of the agent using the period-by-period budget constraints. In particular, show the Euler equation. b. Using the given functional form, write the Euler equation between time 1 and time 3 . In other words, show how c1 and c3 are related. c. Write the present discounted value of optimal lifetime consumption as a function of c0 (and, potentially, other parameters or exogenous variables). d. Write the present discounted value of optimal lifetime utility as a function of c0 (and, potentially, other parameters or exogenous variables). e. Find the present discounted value of lifetime income as a function of y0 (and, potentially, other parameters or exogenous variables) when income is growing each period at the rate of γ, where 0<γ0 ? Explain!
Answers
a. U'(ct) = β(1 + r)U'(ct+1). This equation is known as the Euler equation, which represents the intertemporal marginal rate of substitution between consumption at time t and consumption at time t+1.
b. U'(c1) = β(1 + r)^2U'(c3). This relationship shows that the marginal utility of consumption at time 1 is equal to the discounted marginal utility of consumption at time 3.
c. C0 = ∑t=0[infinity](β(1 + r))^tct. This equation represents the sum of the discounted values of consumption at each period, where the discount factor β(1 + r) accounts for the diminishing value of future consumption.
d. U0 = ∑t=0[infinity](β(1 + r))^tln(ct). This equation represents the sum of the discounted values of utility at each period, where the discount factor β(1 + r) reflects the time preference and the logarithmic utility function captures the agent's preference for consumption.
Y0 = y0 + (1 + γ)y1 + (1 + γ)^2y2 + ..., where γ represents the growth rate of income.
a. The optimization problem of the representative agent involves maximizing the present discounted value of utility subject to the period-by-period budget constraint. The Euler equation is derived as follows:
At each period t, the agent maximizes the utility function U(ct) = ln(ct) subject to the budget constraint ct = (1 + r)wt + yt, where wt is the agent's wealth at time t. Taking the derivative of U(ct) with respect to ct and applying the chain rule, we obtain: U'(ct) = β(1 + r)U'(ct+1). This equation is known as the Euler equation, which represents the intertemporal marginal rate of substitution between consumption at time t and consumption at time t+1.
b. The Euler equation between time 1 and time 3 can be written as U'(c1) = β(1 + r)U'(c2), where c1 and c2 represent consumption at time 1 and time 2, respectively.
Similarly, we can write the Euler equation between time 2 and time 3 as U'(c2) = β(1 + r)U'(c3). Combining these two equations, we fin
d U'(c1) = β(1 + r)^2U'(c3). This relationship shows that the marginal utility of consumption at time 1 is equal to the discounted marginal utility of consumption at time 3.
c. The present discounted value of optimal lifetime consumption can be written as C0 = ∑t=0[infinity](β(1 + r))^tct. This equation represents the sum of the discounted values of consumption at each period, where the discount factor β(1 + r) accounts for the diminishing value of future consumption.
d. The present discounted value of optimal lifetime utility can be written as U0 = ∑t=0[infinity](β(1 + r))^tln(ct).
This equation represents the sum of the discounted values of utility at each period, where the discount factor β(1 + r) reflects the time preference and the logarithmic utility function captures the agent's preference for consumption.
e. The present discounted value of lifetime income, denoted as Y0, can be expressed as Y0 = y0 + (1 + γ)y1 + (1 + γ)^2y2 + ..., where γ represents the growth rate of income. The income in each period is multiplied by (1 + γ) to account for the increasing income over time.
This assumption of income growth allows for a more realistic representation of the agent's economic environment, where income tends to increase over time due to factors such as productivity growth or wage increases.
for such more questions on equation
https://brainly.com/question/17145398
#SPJ8
Can someone plz help me on this one
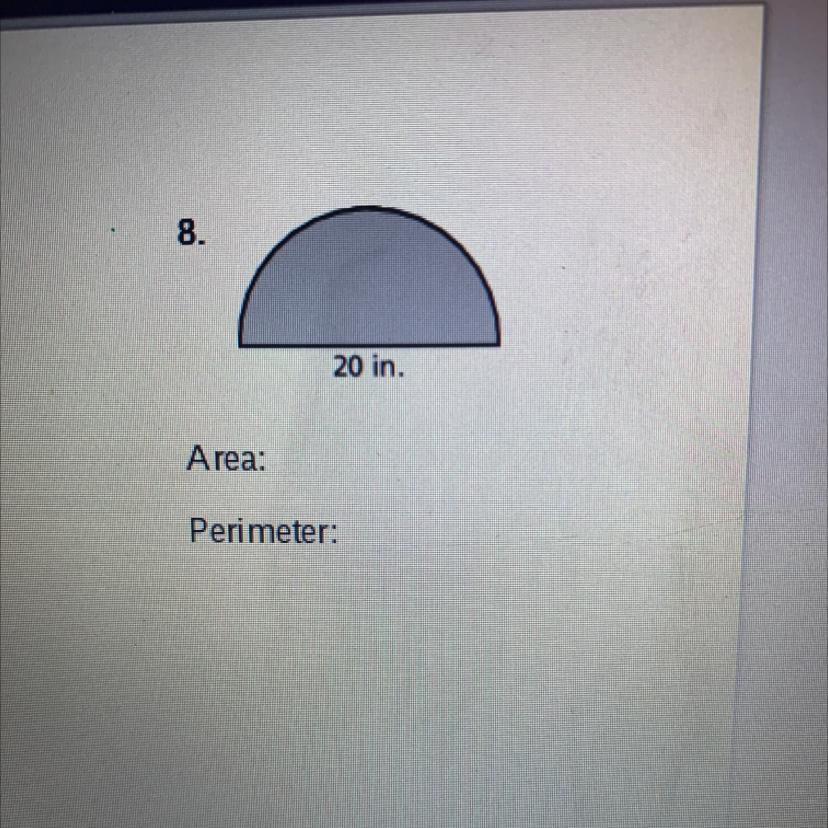
Answers
For the perimeter use the formula 2x3.14xr
step 1: divide the 20 by 2
step2:multiply 3.14 by the qoutient of the division
step3:divide again by 2
For the area the formula is 3.14 x r x r
the r is the qoutient on step one
step 1: multiply both Rs
step2: multiply the 3.14 by the product of step one.
and you are done i hope it helps you
(5z+5)+(7z+4) what is this confused ?
Answers
Answer:
U have to solve this equation\((5z + 5) \: + \: (7z + 4)\)
\(5z + 5 - 7z - 4\)
\(5z - 7z + 5 - 4\)
\(2z + 1\)
hope this helps you !!Write the equation of the line fully simplified slope-intercept form.

Answers
A good trick to use to find the slope is count how high and how far you must go from one point to another to find the slope. (Rise over Run)
The box plots display data collected when two teachers asked their classes how many pencils they lose in a school year.
A box plot uses a number line from 5 to 47 with tick marks every one unit. The box extends from 8 to 14 on the number line. A line in the box is at 11. The lines outside the box end at 7 and 45. The graph is titled Mr. Johnson's Class, and the line is labeled Number Of Pencils.
A box plot uses a number line from 0 to 51 with tick marks every one unit. The box extends from 12 to 21 on the number line. A line in the box is at 14.5. The lines outside the box end at 0 and 50. The graph is titled Mr. Simpson's Class, and the line is labeled Number Of Pencils.
Which class lost the most pencils overall based on the data displayed?
Mr. Simpson's class; it has a larger median value 14.5 pencils
Mr. Johnson's class; it has a larger median of 11 pencils
Mr. Simpson's class; it has a narrow spread in the data
Mr. Johnson's class; it has a wide spread in the data
Answers
The class that lost the most pencils overall based on the data displayed is D. Mr. Johnson's class; it has a wide spread in the data
How to explain the informationThe answer is Mr. Johnson's class. The median is the middle value in a set of data. In Mr. Johnson's class, the median is 11 pencils. This means that half of the students in his class lost 11 or fewer pencils, and half of the students lost 11 or more pencils.
In Mr. Simpson's class, the median is 14.5 pencils. This means that half of the students in his class lost 14.5 or fewer pencils, and half of the students lost 14.5 or more pencils.
Since the median for Mr. Johnson's class is lower than the median for Mr. Simpson's class, we can conclude that Mr. Johnson's class lost more pencils overall.
Learn more about median on
https://brainly.com/question/14532771
#SPJ1
problem 4. if a is a skew symmetric n xn matrix such that n is an odd number, evaluate det(a).
Answers
The determinant of the transpose of A is equal to the determinant of A. And since the transpose of a skew-symmetric matrix is its negative, this implies that the determinant of A should also be equal to its negation. The only possible value that satisfies this condition is zero. Therefore, det(A) = 0 when "n" is an odd number.
We can use the property of skew-symmetric matrices, which states that the determinant of a skew-symmetric matrix of odd order is always 0. This means that for the given matrix A, which is skew-symmetric and of order n, where n is odd, det(A) = 0. In order to prove this property, we can use the fact that the determinant of a matrix is equal to the product of its eigenvalues. Since A is skew-symmetric, all its eigenvalues are imaginary and come in pairs of the form λ and -λ. Since n is odd, there is at least one eigenvalue that is equal to 0, and therefore det(A) = 0. The answer to problem 4 is that the determinant of the skew-symmetric n x n matrix A, where n is an odd number, is equal to 0.
When dealing with a skew-symmetric matrix "A" of odd order "n" (n x n matrix), the determinant of A is always zero.
In a skew-symmetric matrix, the elements below the main diagonal are the negation of the elements above the main diagonal, and the elements on the main diagonal are zero. Mathematically, this can be represented as A(i,j) = -A(j,i) for all i and j. Since "n" is an odd number, multiplying an odd number of negative pairs will result in a negative value for the determinant.
To know more about transpose visit :-
https://brainly.com/question/2263930
#SPJ11
PLEASE HELP!! THIS IS CONFUSING!! Given f (x) = 2/3x -1, complete Parts A and B. Part A: Using the table provided, create five points to demonstrate that for the function f (x) = 2/3x -1, there is exactly one output value for each corresponding input value. In your final answer, include all calculations and the completed table. Part B: On a separate sheet of paper, use the points created in Part A to graph the function f (x) = 2/3x -1. Label the values on the x - and y-axes, and all points on the graph.
Answers
x y
0 -1
3 1
(I tried to make a table above with x,y)
The x intercept is (3/2, 0)
The y intercept is (0, -1)
Slope 2/3
See pic for graph

If anyone can help :)

Answers
Answer:
irrational
Step-by-step explanation:
reason
\( - \frac{5}{52} \)
Someone please help I don’t understand this

Answers
to get the equation of any straight line, we simply need two points off of it, again, let's use the ones from the table in the picture below.
\((\stackrel{x_1}{2}~,~\stackrel{y_1}{7})\qquad (\stackrel{x_2}{4}~,~\stackrel{y_2}{11}) ~\hfill \stackrel{slope}{m}\implies \cfrac{\stackrel{rise} {\stackrel{y_2}{11}-\stackrel{y1}{7}}}{\underset{run} {\underset{x_2}{4}-\underset{x_1}{2}}} \implies \cfrac{ 4 }{ 2 }\implies 2\)
\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{7}=\stackrel{m}{2}(x-\stackrel{x_1}{2}) \\\\\\ y-7=2x-4\implies {\LARGE \begin{array}{llll} y=2x+3 \end{array}}\)

I will send u a picture iof the question
Answers
The expression given is,
\(\frac{1}{4}h+\frac{1}{2}h+\frac{1}{4}h+4=8.\)To determine the value of h , simplify the above expression by taking the lcm .
\(\frac{h+2h+h}{4}+4=8\)\(\frac{4h}{4}=8-4\)\(h=4.\)Thus, the value of h obtained is , 4.
In a sale, the price of a TV is reduced from £250 to £180 what is the decreased percentage?
Answers
Answer:
Step-by-step explanation: 80
Answer: THE ANSWER IS 28%
worked it out on the calculator in the end
Step-by-step explanation:
help! brainliest!!! picture below

Answers
The circumference of a circular garden is 122.46 feet. What is the diameter of the garden? Use 3.14 for pi and do not round your answer.Clude the correct unit in your answer.
Answers
Answer:
38.98
Step-by-step explanation:
d=c/pie
i dont know this is correct
Find the limit, if it exists, or show that the limit does not exist. lim(,)→(0,0) 2 2 4
Answers
The limit does not exist.
What is a limit?A limit in mathematics is the value that a function approaches when its input approaches some value. Limits are used to define continuity, derivatives, and integrals in calculus and mathematical analysis.In order for such a limit to occur, the fraction \(\frac{x^{2} }{x^{2} +y^{2} }\) must be comparable to the same value \(L\), regardless of the way we take to get there \((0,0)\).
Try approaching \((0,0)\) along the x-axis.
This means setting \(y=0\) and finding the limit \(lim_{x-0} \frac{x^{2} }{x^{2} +y^{2} }\).
We obtain:
\(lim_{x-0,y=0}\frac{x^{2} }{x^{2} +y^{2} } =lim_{y=0}}\frac{x^{2} }{x^{2} +0 }\\=lim_{x-0}} \frac{x^{2} }{x^{2} } \\\\=lim_{x-0}}1\\=1\)
Now evaluate approaching \((0,0)\) along the y-axis.
This means setting \(x=0\) and finding the limit \(lim_{y-0} \frac{x^{2} }{x^{2} +y^{2} }\).
\(lim_{y-0,x-0} \frac{x^{2} }{x^{2} +y^{2} } =lim_{y-0} \frac{0}{0+y^{2} } \\=lim_{y-0} \frac{0}{y^{2} } \\=lim_{y-0} 0\\=0\)
Approaching the origin via these two methods results in distinct limits.
\(lim_{x-0,y-0} \frac{x^{2} }{x^{2} +y^{2} }\) ≠ \(lim_{y-0,x-0}\frac{x^{2} }{x^{2} +y^{2} }\)
Therefore the limit does not exist.
Know more about limits here:
https://brainly.com/question/1521191
#SPJ4
The correct question is given below:
Find the limit, if it exists, or show that the limit does not exist.
\(lim_{(x,y) -(0,0)} \frac{x^{2} }{x^{2} +y^{2} }\)
The school library has 286 books. If the school librarian buys 12 books eachmonth for five months, how many books will the library have in all?
Answers
Find the complement in degrees) of the supplement of an angle measuring 115º.
Answers
Given: An angle of measure 115 degrees We know that: The supplement of an angle is equal to 180 degrees minus the angle, and the complement of an angle is equal to 90 degrees minus the angle
Now, we need to find the complement of the supplement of an angle measuring 115 degrees.So, let's first find the supplement of the given angle:
Supplement of 115 degrees = 180 - 115= 65 degrees
Now, we need to find the complement of the above angle which is:
Complement of 65 degrees = 90 - 65= 25 degrees Therefore, the complement of the supplement of an angle measuring 115º is 25 degrees.
To know more about supplement,visit:
https://brainly.com/question/29471897
#SPJ11
can someone help please
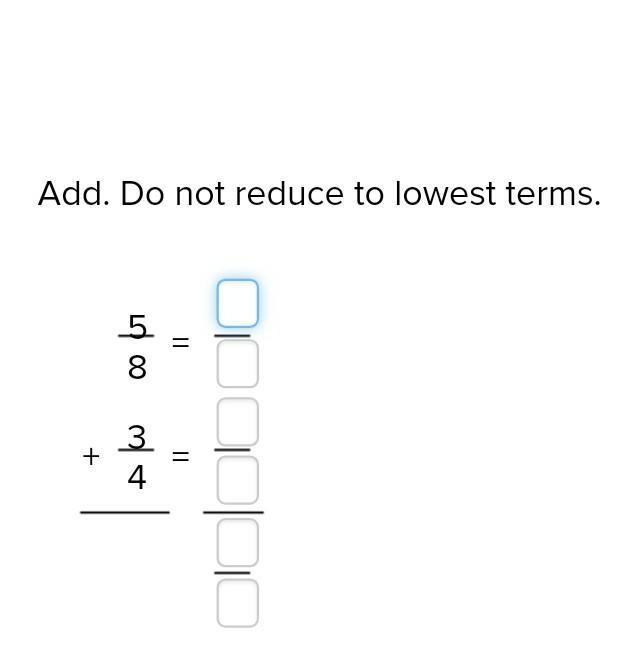
Answers
Answer:
11/8 or, 1 and 3/8
Step-by-step explanation:
First, we have to make both the denominators the same. In this case, we can multiply 3/4 by 2, to make 4, the denominator, into 8. What we do to the denominator, we must do to the numerator! So, we multiply 3 by 2, and get 6!
Now we have, 5/8 + 6/8, which equals 11/8! Which can also be simplified to 1 and 3/8 (because the numerator is larger than the denominator)
Hope this helps! :)
If the mean height is 180cm and the standard deviation is 4. What percentage of the population would lie between 176cm and 184cm?
A.50%
B.68%
C.95%
D.34%
Answers
Standard Deviation: Is a measure of how spread out values are in a data set compared to the mean. It is calculated by finding the square root of the variance, which is the average of the squared differences from the mean.
Mean: The average value of a set of numbers. It is calculated by summing up all the numbers in the set and dividing the result by the total number of numbers in the set.
Distribution Curve: is a bell shaped curve that displays the mean with a line down the center of the curve and standards deviations within standard deviations.
See attached file for model of curve, from: https://commons.wikimedia.org/wiki/File:Standard_deviation_diagram.svg
Given the mean and standard deviation we can use a general rule to determine the population between the given lengths.
Generally in a normal distribution:
68% of the data falls between -1σ and +1σ95% of the data falls between -2σ and +2σ99.75 of the data falls between -3σ and +3σ176 cm is 1 standard deviation less than the mean and 184 cm is 1 standard deviation greater than the mean. Using the general rules above, 68% of data falls between -1σ and +1σ. Therefore, the answer to this question would be B. 68%

What is the rational zero test used to find rational zeros?
Answers
We can use rational zero theorem to find rational zeros.
Given,
Rational zero theorem;-
According to the Rational Zeros Theorem, if P(x) is an integer-coefficient polynomial and is its zero (P() = 0), then p is a factor of P(x constant )'s term and q is a factor of P's leading coefficient (x). The Reasonable Zeros Theorem can be used to locate every rational zero in a polynomial.
Purpose of rational zero test;-
It is also known as the rational root test and the rational zero test. It can be used to locate the polynomial function's zeros. One uses it to determine whether a polynomial has rational zeros or roots. A comprehensive list of the polynomial's potential rational roots is also provided.
Learn more about rational zero test here;-
https://brainly.com/question/16234792
#SPJ4
Find the value of the expression if x = 2.1, z = -4.2 and b = -3.
|2x−z|+6b
Answers
Answer:
\({ \tt{ |2x - z| + 6b}} \\ \\ \dashrightarrow \: { \tt{ |2(2.1) - ( - 4.2)| + 6( - 3) }} \\ \\ \dashrightarrow \: { \tt{ |8.4| - 18 }} \\ \\ { \boxed{ \boxed{ \tt{ \dashrightarrow \: \: - 9.6 \: \: }}}}\)
Suppose a, b denotes of the quadratic polynomial x² + 20x - 2022 & c, d are roots of x² - 20x + 2022 then the value of ac(a - c) ad(a - d) + bc(b - c) + (b - d)
Choose the correct option
(a) 0
(b) 8000
(c) 8080
(d) 16000
Answers
\( \sf\:a,b \: are \: the \: roots \: of \: {x}^{2} + 20x - 2020 = 0 \: and \: \\ \sf \: c,d \: are \: the \: roots \: of \: {x}^{2} - 20x + 2020 = 0 \: then \: \)
\( \sf \: ac(a - c) + ad(a - d) + bc(b - c) + bd(b - d) = \)
(a) 0
(b) 8000
(c) 8080
(d) 16000
\(\large\underline{\sf{Solution-}}\)
Given that
\(\red{\rm :\longmapsto\:a,b \: are \: the \: roots \: of \: {x}^{2} + 20x - 2020 = 0}\)
We know
\(\boxed{\red{\sf Product\ of\ the\ zeroes=\frac{Constant}{coefficient\ of\ x^{2}}}}\)
\(\rm \implies\:ab = \dfrac{ - 2020}{1} = - 2020\)
And
\(\boxed{\red{\sf Sum\ of\ the\ zeroes=\frac{-coefficient\ of\ x}{coefficient\ of\ x^{2}}}}\)
\(\rm \implies\:a + b = - \dfrac{20}{1} = - 20\)
Also, given that
\(\red{\rm :\longmapsto\:c,d \: are \: the \: roots \: of \: {x}^{2} - 20x + 2020 = 0}\)
\(\rm \implies\:c + d = - \dfrac{( - 20)}{1} = 20\)
and
\(\rm \implies\:cd = \dfrac{2020}{1} = 2020\)
Now, Consider
\( \sf \: ac(a - c) + ad(a - d) + bc(b - c) + bd(b - d)\)
\( \sf \: = {ca}^{2} - {ac}^{2} + {da}^{2} - {ad}^{2} + {cb}^{2} - {bc}^{2} + {db}^{2} - {bd}^{2} \)
\( \sf \: = {a}^{2}(c + d) + {b}^{2}(c + d) - {c}^{2}(a + b) - {d}^{2}(a + b)\)
\( \sf \: = (c + d)( {a}^{2} + {b}^{2}) - (a + b)( {c}^{2} + {d}^{2})\)
\( \sf \: = 20( {a}^{2} + {b}^{2}) + 20( {c}^{2} + {d}^{2})\)
\( \sf \: = 20\bigg[ {a}^{2} + {b}^{2} + {c}^{2} + {d}^{2}\bigg]\)
We know,
\(\boxed{\tt{ { \alpha }^{2} + { \beta }^{2} = {( \alpha + \beta) }^{2} - 2 \alpha \beta \: }}\)
So, using this, we get
\( \sf \: = 20\bigg[ {(a + b)}^{2} - 2ab + {(c + d)}^{2} - 2cd\bigg]\)
\( \sf \: = 20\bigg[ {( - 20)}^{2} + 2(2020) + {(20)}^{2} - 2(2020)\bigg]\)
\( \sf \: = 20\bigg[ 400 + 400\bigg]\)
\( \sf \: = 20\bigg[ 800\bigg]\)
\( \sf \: = 16000\)
Hence,
\(\boxed{\tt{ \sf \: ac(a - c) + ad(a - d) + bc(b - c) + bd(b - d) = 16000}}\)
So, option (d) is correct.
