For what values of a are the following expressions true?
1) |a-5|=5-a
2) |a|=-a
Write in inequality format!
PLS HELP
Answers
Answer:
1) a ≤ 5
2) a ≤ 0
Step-by-step explanation:
An absolute value cannot be negative, so for the first expression, we get 5 - a ≥ 0, which simplifies to a ≤ 5.
For the 2nd expression, we know that a can't be negative, which means our equation is -a ≥ 0, which means a ≤ 0.
Related Questions
Consider the roll of a pair of fair dice. Let Ak denote the event that the number of dots facing up is k, for k= 2, ..., 12. (There are 11 such events.) Let Bk denote the event that this number is greater or equal to k. Let E and O denote the events that the number is even or odd, respectively. Find the probabilities: a) P[Ak], and P[BX], for k= 2, ..., 12 b) P[O|B8] c) P[A, U A11\B8] d) P[B80] e) P[B:|B-] f) P[En B,|B8] g) The probability that the two dice show different outcomes
Answers
Ak is the event that the sum of the dots facing up is k, Bk is the event that the sum is greater than or equal to k, E is the event that the sum is even, and O is the event that the sum is odd. The total number of outcomes, which is 36.
a) To find P[Ak], we need to count the number of ways we can obtain a sum of k and divide by the total number of possible outcomes. This gives P[Ak] = (number of ways to obtain k)/(total number of outcomes) = (number of ways to obtain k)/36. Similarly, P[BX] is the probability of obtaining a sum greater than or equal to X, which is the same as the probability of obtaining a sum of X or more, so we can use the same approach as for P[Ak].
b) P[O|B8] is the probability that the sum is odd given that it is greater than or equal to 8. To find this, we can use Bayes' theorem: P[O|B8] = P[O and B8]/P[B8]. We can calculate P[O and B8] by counting the number of outcomes where the sum is odd and greater than or equal to 8, which is 10 (9, 11, ..., 19), and divide by the total number of outcomes that satisfy B8, which is 25 (8, 9, ..., 12). Therefore, P[O and B8] = 10/36 and P[B8] = 25/36, so P[O|B8] = (10/36)/(25/36) = 2/5.
c) P[A U A11\B8] is the probability that the sum is either 2, 3, ..., 11 or 12, but not 8. To find this, we can add the probabilities of the individual events and subtract the probability of their intersection: P[A U A11\B8] = P[A2] + P[A3] + ... + P[A11] + P[A12] - P[B8]. Note that P[B8] is the probability that the sum is 8 or more, so we can use our previous calculation to find this.
d) P[B80] is the probability that the sum is 8 or more. We can count the number of outcomes where the sum is 8 or more, which is 25 (8, 9, ..., 12), and divide by the total number of outcomes, which is 36.
e) P[B:|B-] is the probability that the sum is even given that it is odd. To find this, we can use Bayes' theorem: P[B:|B-] = P[B: and B-]/P[B-]. We can count the number of outcomes where the sum is even and odd, which is 18, and divide by the total number of outcomes where the sum is odd, which is 18 (1, 3, ..., 11), so P[B: and B-] = 18/36 = 1/2. We can also count the number of outcomes where the sum is odd, which is 18, and divide by the total number of outcomes, which is 36, to find P[B-].
f) P[E|B8] is the probability that the sum is even given that it is greater than or equal to 8. To find this, we can use Bayes' theorem: P[E|B8] = P[E and B.
Learn more about Number:
brainly.com/question/17429689
#SPJ11
I need help With this Math assighnment.
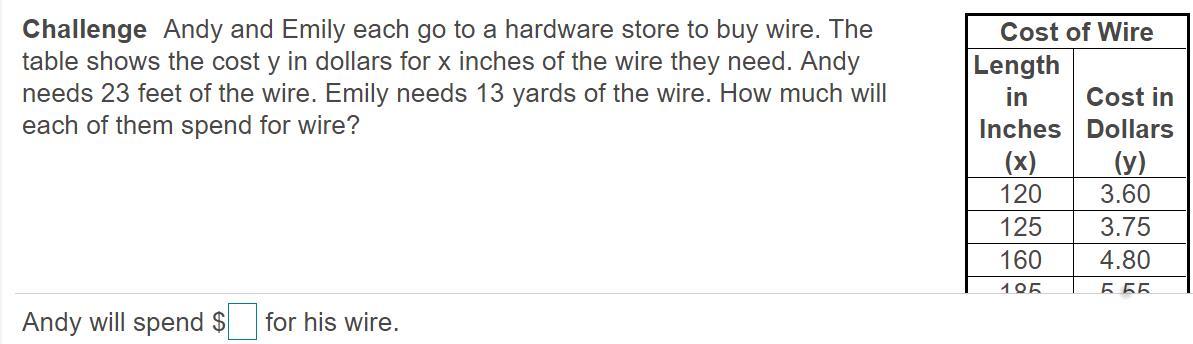
Answers
Answer:
$3.60
Step-by-step explanation:
Hope this helped
Please help me solve this...

Answers
X=-4
let f(p) = 15 and f(q) = 20 where p = (3, 4) and q = (3.03, 3.96). approximate the directional derivative of f at p in the direction of q.
Answers
The approximate directional derivative of f at point p in the direction of q is 0.
To approximate the directional derivative of f at point p in the direction of q, we can use the formula:
Df(p;q) ≈ ∇f(p) · u
where ∇f(p) represents the gradient of f at point p, and u is the unit vector in the direction of q.
First, let's compute the gradient ∇f(p) at point p:
∇f(p) = (∂f/∂x, ∂f/∂y)
Since f(p) = 15, the function f is constant, and the partial derivatives are both zero:
∂f/∂x = 0
∂f/∂y = 0
Therefore, ∇f(p) = (0, 0).
Next, let's calculate the unit vector u in the direction of q:
u = q - p / ||q - p||
Substituting the given values:
u = (3.03, 3.96) - (3, 4) / ||(3.03, 3.96) - (3, 4)||
Performing the calculations:
u = (0.03, -0.04) / ||(0.03, -0.04)||
To find ||(0.03, -0.04)||, we calculate the Euclidean norm (magnitude) of the vector:
||(0.03, -0.04)|| = sqrt((0.03)^2 + (-0.04)^2) = sqrt(0.0009 + 0.0016) = sqrt(0.0025) = 0.05
Therefore, the unit vector u is:
u = (0.03, -0.04) / 0.05 = (0.6, -0.8)
Finally, we can approximate the directional derivative of f at point p in the direction of q using the formula:
Df(p;q) ≈ ∇f(p) · u
Substituting the values:
Df(p;q) ≈ (0, 0) · (0.6, -0.8) = 0
Know more about directional derivative here:
https://brainly.com/question/30365299
#SPJ11
Help Me Please!!!!!!!

Answers
Answer:
4 plates with 2 apples and 5 apricots per plate
Step-by-step explanation:
you are welcome
you have an srs of 23 observations from a large population. the distribution of sample values is roughly symmetric with no outliers. what critical value would you use to obtain a 98% confidence interval for the mean of the population?
Answers
The Critical value to be used to gain the 98 confidence interval for the population mean is2.508 and can be determined using the t- distribution table.
critical value is the value of a test statistic that defines the upper and lower bounds of the confidence interval or determines the position of statistical significance in a statistical test.
Given
You have an SRS of 23 compliances from a large population.The distribution of the sample values is roughly symmetric, with no outliers.98% confidence interval.The following way can be carried out to determine the critical value
Step 1-First determine the degrees of freedom using the following formula
degrees of freedom = n- 1
where n is the sample size.
Step 2- Replace" n" in the below formula.
degrees of freedom = 23- 1
= 22
Step 3- Now you can use the t- distribution table to determine the critical value to get a 98 confidence interval.
critical value = 2.508
To know more about Critical Value,
brainly.com/question/29490388
# SPJ4
Why do we prefer Logistic Regression over Linear Regression for classification problems? O (1), (2) & (3) The predicted values are much more interpretable as they lie in the range of 0 to 1. The sigmoid curve fits the data better than a straight line. Linear regression minimizes the mean squared error whereas logistic regression uses maximum likelihood estimation to estimate parameters.
Answers
Logistic Regression is preferred over Linear Regression for classification problems for several reasons.
Firstly, the predicted values in Logistic Regression are much more interpretable as they lie in the range of 0 to 1, which represents the probability of a certain outcome occurring. In contrast, Linear Regression predicts continuous values which are difficult to interpret as probabilities.
Secondly, the sigmoid curve used in Logistic Regression fits the data better than a straight line used in Linear Regression. This is because the sigmoid curve captures the non-linear relationships between the input variables and the output variable, which is often the case in classification problems.
Lastly, Logistic Regression uses maximum likelihood estimation to estimate parameters, whereas Linear Regression minimizes the mean squared error. Maximum likelihood estimation is a more appropriate method for estimating parameters in classification problems as it takes into account the binary nature of the output variable. Linear Regression, on the other hand, does not consider this binary nature and may not produce accurate results in classification problems.
In summary, Logistic Regression is preferred over Linear Regression for classification problems because of its interpretable predicted values, better fit to non-linear relationships, and appropriate method of estimating parameters using maximum likelihood estimation.
We prefer Logistic Regression over Linear Regression for classification problems for the following reasons:
1) Predicted values in Logistic Regression are more interpretable as they lie in the range of 0 to 1, representing probabilities of class membership, while Linear Regression predicts continuous values which may not directly indicate class membership.
2) The sigmoid curve in Logistic Regression fits the data better for classification problems, as it represents a natural threshold between classes, while a straight line from Linear Regression may not provide clear separation between classes.
3) Logistic Regression uses maximum likelihood estimation to estimate parameters, which makes it more suitable for classification problems as it finds the best fit for the probability of class membership. Linear Regression minimizes the mean squared error, which focuses on minimizing the distance between predicted and actual values, but does not directly optimize for class membership probabilities.
Learn more about Linear Regression:
brainly.com/question/29665935
#SPJ11
The sum of three numbers is 78. The second number is 10 more than the first, and the third number is two times the second number.
1. Write an equation that will help you determine the 3 numbers.
2. Solve the equation showing all your steps.
3. Tell what the 3 numbers are.
Answers
Step-by-step explanation:
a+b+c=78
b=10+a
c=2b
then, we back the first
a+10+a+2b=78
2a+2b=78- 10
2a+2(10+a)=68
2a+2a=48
4a=48
a=12
b=22
c=44
pla shop mathematics

Answers
The number of trees more than 10m tall but not more than 20m tall is 18 trees.
How many of the trees are more than 10m tall but not more than 20m tall?0 < h ≤ 5 = 5
height greater than 0m less than or equal to 5m
5 < h ≤ 10 = 9
height greater than 5m less than or equal to 10m
10 < h ≤ 15 = 13
height greater than 10m less than or equal to 15m
15 < h ≤ 20 = 5
height greater than 15m less than or equal to 20m
20 < h ≤ 25 = 1
height greater than 20m less than or equal to 25m
The number of trees that are more than 10m tall but not more than 20m tall are;
10 < h ≤ 15 = 13
15 < h ≤ 20 = 5
So,
13 + 5 = 18 trees
Therefore, the total number of trees which are 10m tall but not more than 20m tall is 18 trees.
Read more on inequality:
https://brainly.com/question/25275758
#SPJ1
the sum of two numbers is 43, and their differences is 7. find the smaller numbers
Answers
Answer:
18
Step-by-step explanation:
Let x be the smaller number. The larger number would be...
x+7 as the question states their difference is 7.
We can use this to set up an equation:
x+x+7=43
Combine like terms
2x+7=43
Subtract 7 from both sides
2x=36
Divide both sides by 2
x=18
The smaller number is 18
Find all of the roots of the given equation x^{4}-2=0 x= (Use a comma to separate answers as needed. Type radicals and j as needed.)
Answers
The roots of the equation x⁴ - 2 = 0 are ±√2 and ±i√2.
To find the roots of the given equation x⁴ - 2 = 0, we need to solve for x. By rearranging the equation, we have x⁴= 2. To isolate x, we take the fourth root of both sides of the equation.
The fourth root of 2 can be expressed as two sets of roots: ±√2 and ±i√2. The symbol "±" indicates that there are two possible values for each set of roots. The first set of roots, ±√2, represents the real solutions to the equation, while the second set of roots, ±i√2, represents the complex solutions. The letter "i" represents the imaginary unit, which is defined as the square root of -1.
When we substitute these roots back into the original equation, we find that each root satisfies the equation x⁴ - 2 = 0. For example, if we substitute √2 into the equation, we get (√2)⁴ - 2 = 0, which simplifies to 2 - 2 = 0.
In summary, the roots of the equation x⁴ - 2 = 0 are ±√2 and ±i√2, encompassing both real and complex solutions.
Learn more about Roots of the equation
brainly.com/question/14393322
#SPJ11
consider the matrix : what is the minimal approximation error achievable by a rank-1 approximation to ?
Answers
The minimal approximation error A-A 2achievable by a rank-1 approximation A to A is
||A - A1||₂=0 where A is 2×2 matrix.
We have given a matrix A as seen in above figure or A = [ 5 15 ; 6 18 ; -1 -3 ; -4 -12 ; 2 6]
note here that C₂= 3C₁
where Cᵢ --> iᵗʰ column
v = [ 5 ; 6 ; -1 ; -4 ; 2]
||v||² = 82 => ||v|| = √82
and A At v = 820 v
and A At = [ 82 246 ; 246 738]
AAt [1;3] = 820[1;3]
=> v1 = 1/√10(1,3)^t
Then the best rank of 1 approx
= √820 /√80√10 [ 5 ; 6 ; -1 ; -4 ; 2] [ 1 3]
= A
Since , the rank of matrix A is one so, the minimal approx. value is ||A - A1||2 = 0
Hence, the minimal Approx. ||A - A1||2 = 0 .
To learn more about minimal of matrix, refer:
https://brainly.com/question/19084291
#SPJ4
Complete question:
Consider the matrix A: A = [5 15] 6 18 -1 -3 -4 -12 [26] What is the minimal approximation error A-A 2 achievable by a rank-1 approximation A to A? Hint: Can you determine this without explicitly calculating the SVD?

a population grows according to the given logistic equation, where t is measured in weeks. (a) what is the carrying capacity? what is the value of k? (b) write the solution of the equation. (c) what is the population after 10 weeks?
Answers
Answer:
Step-by-step explanation:
P(t) = K / (1 + (K/P0 - 1) * e^(-rt))
In this equation, P(t) is the population at time t, P0 is the initial population at time t=0, K is the carrying capacity, r is the intrinsic growth rate, and e is the base of the natural logarithm ( approximately 2.71828).
To find the carrying capacity, you can set P(t) equal to K and solve for t. This will give you the time at which the population reaches its carrying capacity.
To find the value of k, you can plug in the values for P(t), P0, and r and solve for K.
To write the solution of the equation, you can solve for t by rearranging the equation and taking the natural logarithm of both sides.
To find the population after 10 weeks, you can plug in the values for P0, K, r, and t=10 into the equation and solve for P(t).
I hope this helps! Let me know if you have any further questions.
please help me i can't do it. The bees represent 4 times around the Earth to make 1 kg of honey. Knowing that the radius of the Earth measures 6,371 km, how many kilometers do the bees travel to obtain the 30 kg of honey produced in the hive?
Answers
According to the information, it can be inferred that the bees must travel a distance of 4,803,620.82 km to complete the 30 kg of honey that a hive produces.
How to calculate the distance that bees record to produce honey?To calculate the distance that bees register to produce honey we must perform the following operation.
1. Calculate how many kilometers are equal to the circumference of the earth with the following formula 2*pi*R. In this case we replace the R, by the radius of the earth and we will obtain the distance of the circumference of the earth.
\(2\pi r\)
\(2\pi 6,371 km = 40,030.1736\)
2. Once we have identified the circumference of the earth, we must multiply it by four to know how much distance the bee will recover to produce one kg of honey.
40,030.1736 * 4 = 160,120.694
3. Finally we must multiply the distance it takes to produce 1kg by 30 to find the distance it takes to produce 30kg of honey.
160,120,694 * 30 = 4,803,620.82
learn more about honey in: https://brainly.com/question/14517218
#SPJ1
what will a 20kg bag weigh if it's mass is increased by 40%
Answers
Answer:
28
Step-by-step explanation:
20 x 1.4 = 28
An increase of 40% is the same as multiplying by the multiplier 1.4
Determine the value of c that makes thefunction f(x, y) = ce^−2x−3y a jointprobability density function over the range 0
Answers
the value of c that makes the function f(x, y) = ce^−2x−3y a joint probability density function over the given range is:
\(c = -6 / (e^−5-1)\)
To determine the value of c that makes the function f(x, y) = \(ce^−2x−3y\) a joint probability density function over the range 0 ≤ x ≤ 1 and 0 ≤ y ≤ 1, we need to make sure that the function integrates to 1 over this range. This is because the total probability over the entire range should equal 1.
Step 1: Set up the double integral
To ensure that the function integrates to 1, we can set up a double integral over the given range:
∫∫ f(x, y) dx dy = 1
Step 2: Plug in the function and limits
Now we can plug in the function and the limits for x and y:
∫₀¹ ∫₀¹ ce^−2x−3y dx dy = 1
Step 3: Integrate with respect to x
Integrate the function with respect to x:
∫₀¹ [(-c/2)e^−2x−3y]₀¹ dy = 1
Evaluate the integral at the limits:
∫₀¹ [-c/2(e^−2−3y - e^−3y)] dy = 1
Step 4: Integrate with respect to y
Now integrate with respect to y:
[-c/6(e^−5 - 1)]₀¹ = 1
Evaluate the integral at the limits:
- c/6(e^−5 - 1) = 1
Step 5: Solve for c
Finally, solve for c:
c = -6 / (e^−5 - 1)
So, the value of c that makes the function f(x, y) = ce^−2x−3y a joint probability density function over the given range is:
c = -6 / (e^−5 - 1)
To know more about joint probability density function refer here:
https://brainly.com/question/14283399
#SPJ11
how to solve numbers 4-5

Answers
Answer:
x^2+7x+6
Step-by-step explanation:
.............................
...................... ......

Answers
Answer:
a = 20
b = 10
Or if in coordinate format, (20,10)
Step-by-step explanation:
\(\left \{ {{4a-3b=50} \atop {5a-2b=80}} \right.\)
Solve the system using elimination:
In elimination, you want to eliminate a term. I want to eliminate b, so what I would do is to get it the same coefficient (LCM)
\(\left \{ {4a - 3b=50} \atop {5a-2b=80}} \right.\)\(\left \{ {{8a-6b=100} \atop {15a-6b=240}} \right.\) <= Multiply the equations by 3 to find LCM\(-7a = -140\\\) Remember, if the terms you want to eliminate have the same sign in front of them ( - or +), subtract the top equation from the bottom. If they are different signs, add the two equations. \(a=20\)Now, plug in 20 for an into any of the original equations
4a - 3b = 504(20) - 3b = 5080 - 3b = 50-3b = -30b = 10The solution of the system is written as a coordinate, in alphabetical order. Since the variables are a and b, you write it as (a,b).
The solution is \(\boxed{(20,10)}\)
-Chetan K
An iguana is about 42 cm. at birth and increases in length at an approximate rate of 12% per week. Write the function which models the growth. Use X for the number of weeks and y for the length of the iguana.

Answers
We were given that:
The iguana is 42cm at birth
It increases by 12% every week; r = 12% = 0.12
The number of weeks is represented by ''x'' & the length of the Iguana is represented by ''y''
This function is represented by the expression below:
\(\begin{gathered} f\mleft(x\mright)=a\mleft(1+r\mright)^x \\ where\colon r=growth.rate \\ a=initial.length \\ f\mleft(x\mright)=y \\ \Rightarrow y=a(1+r)^x \\ y=a(1+r)^x \\ a=42,r=0.12 \\ \text{Substituting the variables into the equation, we have:} \\ y=42(1+0.12)^x \\ y=42(1.12)^x \\ \\ \therefore y=42(1.12)^x \end{gathered}\)A athlete runs a distance of 1500 metres in 3
minutes and 50 seconds.
Work out the average speed of the athlete.
Give your answer, in metres per second, to 1
decimal place.
Answers
Answer:
6.5m/sec
Step-by-step explanation:
speed = distance
time
= 1500 1 min = 60 seconds
230 3 min = 180 seconds
180 + 50
= 6.5217391304 = 230
Round off to 1 decimal place = 6.5
What is the sum of (8a+2b-4)
Answers
Answer:
2(4a+b-2)
Step-by-step explanation:
All you need to do is factor out 2 from the expression. (sorry if this is wrong)
How do you write 950% as a fraction, mixed number, or whole number?
Answers
Step 1: Write down the percent divided by 100 like this:
950% = 950/100
Step 2: Multiply both top and bottom by 10 for every number after the decimal point:
As 950 is an integer, we don't have numbers after the decimal point. So, we just go to step 3.
Step 3: Simplify (or reduce) the above fraction by dividing both numerator and denominator by the GCD (Greatest Common Divisor) between them. In this case, GCD(950,100) = 50. So,
(950÷50)/(100÷50) = 19/2 when reduced to the simplest form.
As the numerator is greater than the denominator, we have an IMPROPER fraction, so we can also express it as a MIXED NUMBER, thus 950/100 is also equal to 9 1/2 when expressed as a mixed number.
What is the rate of change of the function shown on the graph? Round to the nearest tenth.
Answers
An angle that shares the same sine value of an angle that measures StartFraction 5 pi Over 4 EndFraction radians is located where? Quadrant I Quadrant II Quadrant IV along an axis.
Answers
The angle can be described by plotting a terminal side of the angle on a
graph that is rotated clockwise from the horizontal axis.
The best option for the location of the is; Quadrant IVReasons:
The angle which shares the same sine value with the required angle = \(\displaystyle \frac{5 \cdot \pi}{4}\)
Let θ represent the angle, we have;
\(\displaystyle sin(\theta) = \mathbf{ sin\left( \frac{5 \cdot \pi}{4}\right)} = -\frac{\sqrt{2} }{2}\)
Given that the sine of the angle is negative and that the sine of angles in
Quadrant I and Quadrant II are positive, we have that the location of the
angle is in Quadrant III or Quadrant IV.
Therefore, the best option for the location of the angle is; Quadrant IV
Learn more about the Quadrants of the coordinate plane here:
https://brainly.com/question/10198343
Answer: c Quadrant IV
Step-by-step explanation: edge
Try this!
Arrange the following set of numbers in increasing and decreasing orders.
1.{3, -4, 0, 6, -2}
2.{2.5, 0.3, 5.25, -0.7, 1.2}
3. {2, 0.8 -√8, -4.7, 6⅓}
Decreasing:____________
Increasing:____________
Decreasing:____________
Increasing:____________
Decreasing:____________
Increasing:____________
all time let us have a review about your past topic about multiplying numbers by power of 10
1. 0.042 x 10=
2. 7.331 x 100=
3 0.125 x 1000 =
4. 1.031 x 0.1=
5. 21.5 x 0.001 =
need now
:plss wag nyu na ih answer kung mali rin ih answer nyu huhh!

Answers
Answer:
23446
76532
12839
09192
29292
Consider the glven solids with the dimensions shown. Which solids are similar?
A. only figure 1 and figure 2
B. only figure 1 and figure 3
C. only figure 2 and figure 3
D. all three figures

Answers
Answer:
A) only figure 1 and figure 2
Step-by-step explanation:
Answer: Choice A) only figure 1 and figure 2
===========================================================
Explanation:
Let's assume that figure 2 is similar to figure 3.
If this is the case, then the horizontal portions would divide to 30/15 = 2, showing that figure 3 has sides that are twice as long compared to figure 2. But then notice that the vertical sides divide to 36/24 = 1.5, which doesn't match with the previous result of 2.
Figures 2 and 3 cannot be similar for that reason.
Also, figures 1 and 3 are not similar either. Note the horizontal portions divide to 30/10 = 3 while the vertical portions divide to 36/16 = 2.25; the results 3 and 2.25 don't match.
We eliminate answers B, C and D. The only thing left is choice A.
-------------------
To verify choice A is true, we divide each corresponding piece like so
Horizontal: 15/10 = 1.5Vertical: 24/16 = 1.5Slanted: 12/8 = 1.5Each division leads to the same result of 1.5, meaning that figure 2's side lengths are 1.5 times longer than the corresponding side lengths of figure 1. So this confirms that figure 1 is similar to figure 2.
8. if u is uniform on [0,1], find the density function of √u .
Answers
The density function of √u, where u is uniformly distributed on [0,1], is f(v) = 2√v for 0 ≤ v ≤ 1.
To find the density function of √u, where u is uniformly distributed on the interval [0,1], we can use the transformation method.
Let's denote the random variable √u as v = √u. We want to find the probability density function (PDF) of v.
First, we find the cumulative distribution function (CDF) of v:
F(v) = P(v ≤ x) = P(√u ≤ x) = P(u ≤ x²) = x², for 0 ≤ x ≤ 1.
Next, we differentiate the CDF to obtain the PDF of v:
\(\begin{equation}f(v) = \frac{d}{dv} F(v) = \frac{d}{dv} (x^2) = 2x, \quad 0 \leq x \leq 1\)
However, we need to express the PDF in terms of v, not x. Since v = √u, we can substitute x = √v into the PDF:
f(v) = 2√v, for 0 ≤ v ≤ 1.
Therefore, the density function of √u is f(v) = 2√v, for 0 ≤ v ≤ 1.
To know more about the density function refer here,
https://brainly.com/question/31696973#
#SPJ11
What are the zeros of this function?
A. x = 0 and x = -6
B. X = 2 and x = -6
C. X = 0 and x = 5
D. x = 0 and x = -5

Answers
Answer:
c
Step-by-step explanation:
the parabola crosses the x axis at (0,0) and (4,0)
In November, the price of a cell phone was double the price in March. In December, the price was $53, which was $25 less than the price in November.
What was the price of the cell phone in March?
The price of the cell phone in March was
Answers
Based on the price of the cell phone in November and December, the price of the cell phone in March was $39
How to find the price of the cell phone?To find the price of the cell phone in March, you need to first find the price of the cell phone in November.
The price of the cell phone in November was $25 more than the price in December:
= 25 + 53
= $78
The price in November was double the price in March so the price in March was:
= 78 / 2
= $39
Find out more on price at https://brainly.com/question/25373544
#SPJ1
A flagpole on level ground casts a shadow 13 meters long when the sun is 26° up from the horizon. How tall is the flagpole?
Answers
Answer:
x= 23780. 6. An airplane climbs at an angle of 18° with the ground. Find the ground distance the plane travels as it moves 2500 m through the air.' 2378m. 1. lighthouse .
Step-by-step explanation:
Answer:
Approximately 6.3405 feet
Step-by-step explanation:
Our trigonometric ratio will be tangent in this case, since we are working with the opposite and adjacent sides.
Our equation that we set up will end up being \(tan\theta=o/a\)
\(tan(26)=x/13\)
\(13tan(26)=x\)
\(13(0.4877) = x\)
\(x=6.3405\)