Given that h(x) = -2x + 5, g(x) =
2x – 7; compute g(h(x))
Answers
-4x+10-7
-4x+3
Related Questions
You are interested in finding a 95% confidence interval for the mean number of visits for physical therapy patients. The data below show the number of visits for 11 randomly selected physical therapy patients. Round answers to 3 decimal places where possible.
13 5 10 11 26 20 18 18 24 23 5
a. To compute the confidence interval use a
t
Correct distribution.
b. With 95% confidence the population mean number of visits per physical therapy patient is between
and
visits.
c. If many groups of 11 randomly selected physical therapy patients are studied, then a different confidence interval would be produced from each group. About
percent of these confidence intervals will contain the true population mean number of visits per patient and about
percent will not contain the true population mean number of visits per patient.

Answers
For finding a 95% confidence interval:
a. To compute the confidence interval, use a t distribution with 10 degrees of freedom.b. With 95% confidence, the population mean number of visits per physical therapy patient is between 13.011 and 19.249 visits.c. About 95% of these confidence intervals will contain the true population mean number of visits per patient and about 5% will not contain the true population mean number of visits per patient.How to solve confidence interval?a) The sample mean is x = 16.13.
The sample standard deviation is s = 6.948.
The degrees of freedom are df = 10.
The critical value of t for a 95% confidence interval is t = 2.228.
The margin of error is ME = t × s/√n = 2.228(6.948)/√11 = 4.263.
The 95% confidence interval is x ± ME = 16.13 ± 4.263 = (11.867, 20.393).
b) The 95% confidence interval is (11.867, 20.393).
This means that we are 95% confident that the true population mean number of visits per physical therapy patient is between 11.867 and 20.393 visits.
c) This is because the confidence interval is a range of values that is likely to contain the true population mean. If many samples of the same size are taken from the same population, then about 95% of the confidence intervals from these samples will contain the true population mean.
Find out more on confidence interval here: https://brainly.com/question/15712887
#SPJ1
Which statements are true? Select each correct answer. Responses Only some triangles are plane figures. Only some triangles are plane figures. All triangles are polygons. All triangles are polygons. All triangles have 3 right angles. All triangles have 3 right angles. All triangles are closed figures. All triangles are closed figures. All triangles have 3 straight sides.
Answers
The three true statements are as follows:
All triangles are polygons.All triangles are closed figures. All triangles have 3 straight sides.What are the true statements?In the list, there are several true statements and some of them include the facts that all triangles are polygons, they are closed figures and they have three straight sides.
A polygon is a shape with two or more sides. Triangles ahve three sides, so we can easily address them as polygons. Also, all triangles are closed figures and they also have three straight sides.
Learn more about triangles here:
https://brainly.com/question/17335144
#SPJ1
What is 4 x 2? Help.
Answers
Answer:
8
Step-by-step explanation:
plss help for brainlist !!

Answers
Answer: multiplication property
The Federal Bureau of Investigation reported the statistics in the following table for
homicides in 2019. Use the data to answer
Weapon: Handgun : 6368 Rifle : 364 Shotgun : 200 Unknown firearm: 3326
Weapon: Cutting instrument: 1476 Other weapons: 1593 Hands, feet, etc: 600 Total: 13927
(i)If there were three unrelated murders in Detroit in June 2019, find the probability that all three were committed with a gun.
(ii)Find the probability that a murder was committed with a handgun given that a gun was used.
(iii) Find the probability that if four unrelated murders are studied, two involved a gun
and two involved a cutting instrument.
Answers
The probability that all three murders were committed with a gun is: 0.252.
The probability that one murder was committed with a gun is:
P(Gun) = (6368 + 364 + 200 + 3326)/13927 = 0.632
Therefore, the probability that all three murders were committed with a gun is:
P(3 Guns) = P(Gun) * P(Gun) * P(Gun) = \(0.632^3\) = 0.252
The probability that a murder was committed with a handgun given that a gun was used is:
P(Handgun | Gun) = P(Handgun and Gun) / P(Gun)
We need to find P(Handgun and Gun). From the table, we see that 6368 murders were committed with a handgun and 6368 + 364 + 200 = 6932 murders were committed with a gun. Therefore:
P(Handgun and Gun) = 6368/13927
And:
P(Handgun | Gun) = (6368/13927) / (6368 + 364 + 200 + 3326)/13927 = 0.542
The probability that two murders involved a gun and two involved a cutting instrument is:
P(2 Guns and 2 Cutting instruments) = (C(4,2) * C(6932,2) * C(1476,2)) / C(13927,4)
Where C(n,r) is the number of combinations of n things taken r at a time.
Thus, calculating this gives: P(2 Guns and 2 Cutting instruments) = 0.150
For more details regarding probability, visit:
https://brainly.com/question/30034780
#SPJ1
Un bloque de vidrio flint tiene un espesor de 4 cm, ¿qué espesor aparenta tener cuando se le ve desde arriba?
Answers
Answer: El índice de refracción del vidrio flint es mayor que el del aire. Cuando la luz pasa de un medio con un índice de refracción menor (como el aire) a un medio con un índice de refracción mayor (como el vidrio), experimenta un cambio de dirección. Este fenómeno se conoce como refracción.
Cuando observamos el bloque de vidrio flint desde arriba, la luz que proviene del bloque sufre refracción al pasar del vidrio al aire. Debido a la refracción, los rayos de luz se desvían y parecen venir de una posición más alta dentro del vidrio de lo que realmente están. Esto crea una ilusión óptica que hace que el espesor aparente del bloque de vidrio se vea más delgado de lo que realmente es.
La cantidad exacta de adelgazamiento aparente depende del ángulo de incidencia de la luz y de los índices de refracción del vidrio y el aire. Sin más información, no es posible determinar el espesor aparente específico del bloque de vidrio flint cuando se ve desde arriba.
Step-by-step explanation:
write the ratio as a fraction in lowest terms. compare in hours.22 hours to 5 days
Answers
We know 1 day = 24 hours
Let's convert 5 days to hours:
\(5\text{days}\times\frac{24\text{hour}}{1\text{day}}=5\times24=120hours\)Now, we have the ratio:
22 hours to 120 hours
We can write it as a fraction:
\(\frac{22}{120}\)This is not in its lowest terms. We can divide numerator and denominator by "2", to get:
\(\frac{22}{120}=\frac{11}{60}\)Thus, final answer is:
11/60
or
\(\frac{11}{60}\)(easy math question please help) find the value of x question #6

Answers
Answer:
Step-by-step explanation:
45+8x+21+90=180 degree(sum of interior angles of a triangle)
156+8x=180
8x=180-156
8x=24
x=24/8
x=3
Which type of relationship is indicated by the residual plot? Non-linear relationship. Linear relationship Exponential relationship

Answers
The type of relationship that is indicated by the residual plot is given as follows:
Non-linear relationship.
How to classify the functions?A function is classified as exponential if when the input variable is changed by one, the output variable is multiplied by a constant.
A function is classified as linear if when the input variable is changed by one, the output variable is increased/decreased by a constant.
For this problem, we have an alternative pattern, where the function neither multiplied nor added/subtracted by a constant value when the input is increased by one, hence we merely classify the relationship as a non-linear relationship.
More can be learned about exponential functions at brainly.com/question/2456547
#SPJ1
x^3 + 3x^2 -10x factor polynomial and find zero
Answers
Answer:
x(x - 2)(x + 5)x = 0, x = 2, x = -5Step-by-step explanation:
x^3 + 3x^2 - 10x
~Factor
x(x - 2)(x + 5)
Solve for the zero.
x(x - 2)(x + 5) = 0
We know that; x = 0, x - 2 = 0, and x + 5 = 0
x = 0
x - 2 = 0
x = 2
x + 5 = 0
x = -5
Best of Luck!
Here we are provided with an polynomial of degree 3 and we have to factorise it first and then we have to compute it's zeroes.
Given Polynomial:
x³ + 3x² - 10xTaking common x from all the 3 terms,
➝ x(x² + 3x - 10)
Factorising through Middle term factorisation,
➝ x(x² + 5x - 2x - 10)
➝ x{x(x + 5) - 2(x + 5)}
➝ x(x - 2)(x + 5)
Hence, Factorised !!
Now equating to 0 to find the zeroes of the poly.
➝ x(x - 2)(x + 5) = 0
That means,
x = 0x - 2 = 0x + 5 = 0So, the zeroes of the polynomial is 0, 2 or -5
And we are done....
Carry On Learning \(!\)
Please help me with this.

Answers
Here are the correct matches to the expressions to their solutions.
The GCF of 28 and 60 is 4.
(-3/8)+(-5/8) = -4/4 = -1.
-1/6 DIVIDED BY 1/2 = -1/6 X 2 = -1/3.
The solution of 0.5 x = -1 is x = -2.
The solution of 1/2 m = 0 is m = 0.
-4 + 5/3 = -11/3.
-2 1/3 - 4 2/3 = -10/3.
4 is not a solution of -4 < x.
1. The GCF of 28 and 60 is 4.
The greatest common factor (GCF) of two numbers is the largest number that is a factor of both numbers. To find the GCF of 28 and 60, we can factor each number completely:
28 = 2 x 2 x 7
60 = 2 x 2 x 3 x 5
The factors that are common to both numbers are 2 and 2. The GCF of 28 and 60 is 2 x 2 = 4.
2. (-3/8)+(-5/8) = -1.
To add two fractions, we need to have a common denominator. The common denominator of 8/8 and 5/8 is 8. So, (-3/8)+(-5/8) = (-3 + (-5))/8 = -8/8 = -1.
3. -1/6 DIVIDED BY 1/2 = -1/3.
To divide by a fraction, we can multiply by the reciprocal of the fraction. The reciprocal of 1/2 is 2/1. So, -1/6 DIVIDED BY 1/2 = -1/6 x 2/1 = -2/6 = -1/3.
4. The solution of 0.5 x = -1 is x = -2.
To solve an equation, we can isolate the variable on one side of the equation and then solve for the variable. In this case, we can isolate x by dividing both sides of the equation by 0.5. This gives us x = -1 / 0.5 = -2.
5. The solution of 1 m = 0 is m = 0.
To solve an equation, we can isolate the variable on one side of the equation and then solve for the variable. In this case, we can isolate m by dividing both sides of the equation by 1. This gives us m = 0 / 1 = 0.
6. -4 + 5/3 = -11/3.
To add a fraction and a whole number, we can convert the whole number to a fraction with the same denominator as the fraction. In this case, we can convert -4 to -4/3. So, -4 + 5/3 = -4/3 + 5/3 = -11/3.
7. -2 1/3 - 4 2/3 = -10/3.
To subtract two fractions, we need to have a common denominator. The common denominator of 1/3 and 2/3 is 3. So, -2 1/3 - 4 2/3 = (-2 + (-4))/3 = -6/3 = -10/3.
8. 4 is not a solution of -4 < x.
The inequality -4 < x means that x must be greater than -4. The number 4 is not greater than -4, so it is not a solution of the inequality.
For more such questions on GCF
https://brainly.com/question/902408
#SPJ8
In ΔTUV, u = 3.4 inches, m∠U=144° and m∠V=35°. Find the length of v, to the nearest 10th of an inch.
Answers
The length of v to the nearest 10th of an inch is 2.0 inches.
What is a triangle?A triangle is a 2-D figure with three sides and three angles.
The sum of the angles is 180 degrees.
We can have an obtuse triangle, an acute triangle, or a right triangle.
We have,
We can use the Law of Sines,
Which states that for any triangle ABC:
a/sin(A) = b/sin(B) = c/sin(C)
where a, b, and c are the lengths of the sides of the triangle opposite the angles A, B, and C.
Now,
a = UV = u = 3.4 inches
A = ∠TUV
= 180° - m∠U - m∠V
= 180° - 144° - 35°
= 1°
B = ∠UTV
= m∠U
= 144°
C = ∠TVU
= m∠V
= 35°
Using the Law of Sines,
v/sin(C) = u/sin(B)
Substituting in the values.
v/sin(35°) = 3.4/sin(144°)
Solving for v.
v = (3.4 × sin(35°)) / sin(144°)
v = 1.97 inches
Therefore,
The length of v to the nearest 10th of an inch is 2.0 inches.
Learn more about triangles here:
https://brainly.com/question/25950519
#SPJ9
Adams watches a movie that is 2 hours 15 minutes long how many minutes is the time
Answers
Answer:
135 minutes
Step-by-step explanation:
Answer:
135 minutes
Step-by-step explanation:
1 hour= 60 minutes
2hours=60x2=120 minutes
120+15=135 minutes
plz mark me as brainliest.
The growth factor for one generation of a bacteria culture is given by the function g(t)=ln(2)t, in which t is the time it takes for the generation to mature to its full size based on the energy resources and environmental conditions available in the culture. What happens to t if g(t) is cut in half?
t=
Points possible: 1
Allowed attempts: 3
Question 2
What happens to t?
If g(t) is cut in half, then t is
Answers
If g(t) is cut in half, then t is doubled. Halving the growth factor halves the rate of growth, reducing the time required for a generation to develop to full size.
What do you mean by growth factor?Growth factor refers to a mathematical expression or a metric that measures the rate of increase or growth of a quantity over time. It is used in many fields such as biology, economics, finance, and others to quantify the increase in size, population, revenue, or any other variable of interest. The growth factor can be represented as a ratio, percentage, or an exponential function and is used to predict future growth based on past trends.
3 potential points
Three tries are permitted.
If g(t) is divided in half, t is also divided in half. This is because the growth factor is a measure of the rate of growth, and halving it equals halves the rate of growth. As a result, the time required for a generation to develop to full size is cut in half.
To know more about rate visit:
brainly.com/question/29765585
#SPJ1
What is 2223810294+ 55367457 + 23523546?
Answers
The radius of a circle is 4 miles. What is the length of a 45° arc?
45°
r=4 mi
Answers
The length of a 45° arc with a radius of 4 miles is approximately 3.14 miles, calculated using the formula for arc length.
To determine the length of a 45° arc given a radius of 4 miles, we can use the formula: Arc length = (angle measure / 360°) x 2πr, where r is the radius of the circle and π is a constant equal to approximately 3.14.
Substituting the given values into the formula, we get: Arc length = (45° / 360°) x 2π(4 mi)Arc length = (1/8) x 2π(4 mi)Arc length = (1/8) x 8π Arc length = π
The length of the 45° arc is approximately 3.14 miles.
Summary: To find the length of a 45° arc of a circle, we use the formula: Arc length = (angle measure / 360°) x 2πr. Given a radius of 4 miles, we can substitute the values into the formula to get the length of the 45° arc, which is approximately 3.14 miles.
For more questions on arc length
https://brainly.com/question/31341388
#SPJ8
A ball is thrown from a height of40 meters with an initial downward velocity of 10 . The ball's height (in meters) after seconds is given by the following.
Answers
Answer:
after 2 seconds
0=40-10t-5t^2
t^2+2t-8=0
(t+4)(t-2)=0
t=-4 or t=2
I think this is correct
What is the sin B?
/21
B
5
2
sin (B) =
[?]
![What is the sin B?/21B52sin (B) =[?]](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/bJqEBQdNtkeNzRPqszdQkxPqXUYlMPak.png)
Answers
Answer:
Step-by-step explanation:
sin (B) = \(\frac{2}{5}\)
A. Is the relation function? Explain.

Answers
The graph represents a functional relationship between two variables X and Y. We get y=3 for the value x=2
What is the domain of a function?Domain is defined as the set of values of independent variables.
In the question, all x coordinates are domain.
What is the range of a function?In a function, for each domain we get a possible output from the dependent variables which is termed as range. In this graph, the y coordinates are range because y value is dependent on x value.
The graph shows five points are plotted on XY coordinate system that represents a relationship between independent variable X and dependent variable Y.
hence, this graph is plotted from a function.
from the graph we get the domain as {-4, -2, 0, 2, 4}
the ranges are = {-3, -2, -1, 1, 3}
we get, y=3 for the value of x= 2
to know more about function visit:
https://brainly.com/question/28278690
#SPJ1
A cardboard box without a lid is to have a volume of 8,788 cm3. Find the dimensions that minimize the amount of cardboard used.
Answers
Answer:
x = y = 26 cm; z = 13 cm
Step-by-step explanation:
We can calculate the dimensions of the square base as
∛(2·8788) = 26 cm
the height of the box will be half of 26/2 which is 13 cm.
x = y = 26 cm; z = 13 cm
then the minimum area for the given volume can be calculated using what we call Lagrange multipliers, this makes it easier
area = xy +2(xz +yz)
But we were given the volume as 8788
Now we will make the partial derivatives of L to be in respect to the cordinates x, y, z, as well as λ to be equal to zero, then
L = xy +2(xz +yz) +λ(xyz -8788)
For x: we have
y+2z +λyz=0
For y we have
y: x +2z +λxz=0
For z we have 2x+2y +λxy=0............eqn(*)
For we have xyz -8788=0
If we simplify the partial derivative equation of y and x above then we have
λ = (y +2z)/(yz).
= 1/z +2/y............eqn(1)
λ = (x +2z)/(xz)
= 1/z +2/x.............eqn(2)
Set eqn(1 and 2) to equate we have
1/z +2/y = 1/z +2/x
x = y
From eqn(*) we can get z
λ = (2x +2y)/(xy) = 2/y +2/x
If we simplify we have
1/z +2y = 2/x +2/y
Then z = x/2
26/2 =13
Therefore,
x = y = 2z = ∛(2·8788)
X= 26
y = 26 cm
z = 13 cm
In a particular library, 18% of the books are children's books, 53% of the books are adult fictions, and the rest are adult non-fiction
You choose one book at random. What is the probability that it is an adult non-fiction book ?
Answers
Answer:
29%
Step-by-step explanation:
You add the 18 and 53 then subtract by 100 to receive your answer
Answer:
29%
Step-by-step explanation:
You add the percentages of the other categories (18 - children, 53 - adult fiction) then subtract from 100.
Please help for 10 ponits
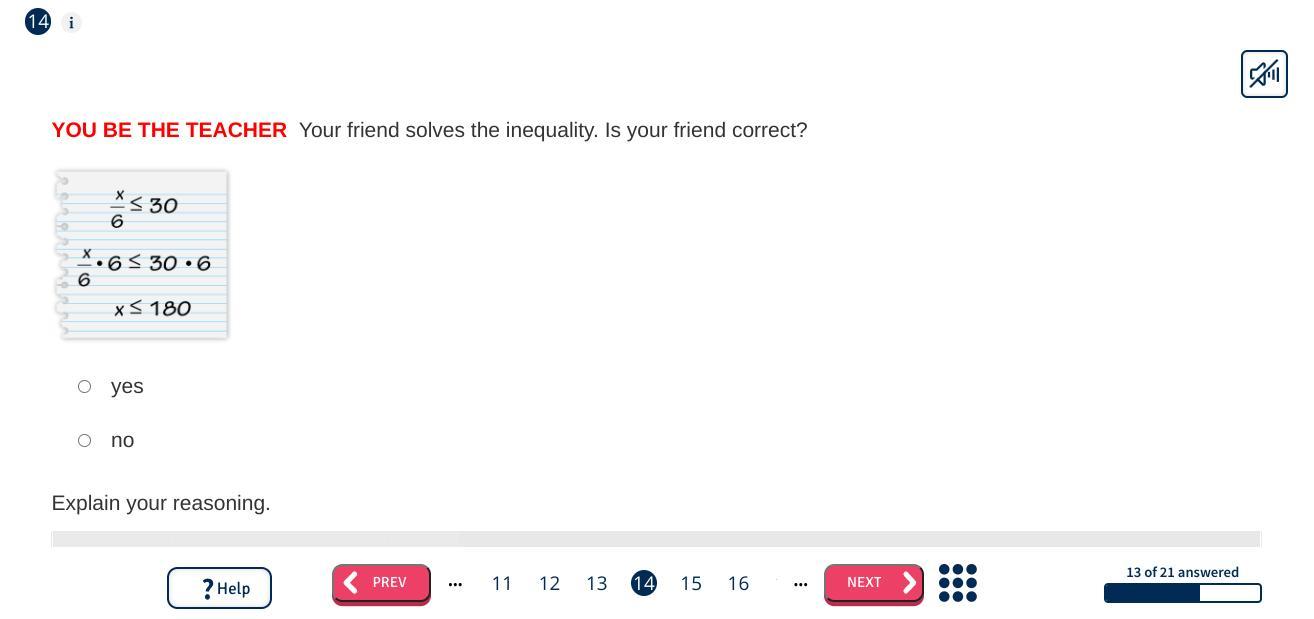
Answers
Answer:
it's a yes
Step-by-step explanation:
X/6 ≤ 30
to find the value of X we have to move the numerical to the other side
in this case the number is 1/6
X * 1/6 ≤ 30
so to balance the both side and get rid of the number on the left side we multiple with 6.
1/6*6 = 1 on the left side
30*6 = 180 on the right side
so the full equation will be
X * 1/6 * 6 ≤ 30 * 6
X * 1 ≤ 180
X ≤ 180
Joe is new to cooking. The probability that joe burns dinner is 50%

Answers
Given that the probability that Joe burns dinner is:
\(p=50\text{\%}=\frac{50}{100}=0.5\)You need to use the following Binomial Distribution Formula, in order to solve the exercise:
\(P(X)=\frac{n!}{(n-x)!x!}\cdot p^x(1-p)^{n-x}\)Where "n" is the sample size, "x" is the number of successes desired, and "p" is the probability of getting a success in a trial.
(a) You must find the probability that in the next 7 dinners Joe prepares, 4 of them will burn. Therefore, for this case:
\(\begin{gathered} n=7 \\ x=4 \end{gathered}\)Then, you can substitute values into the formula and evaluate:
\(P(X=4)=\frac{7!}{(7-4)!4!}(0.5)^4(1-0.5)^{7-4}\)\(P(X=4)\approx0.2734\)(b) You must find the probability that in the next 7 dinners Joe prepares, at least 5 of them will burn. Therefore, since "at least" indicates greater than or equal to 5, you need to set up this Sum for:
\(\begin{gathered} x=5 \\ x=6 \\ x=7 \end{gathered}\)Then:
\(P(X\ge5)=\frac{7!}{(7-5)!5!}(0.5)^5(1-0.5)^{7-5}+\frac{7!}{(7-6)!6!}(0.5)^6(1-0.5)^{7-6}+\frac{7!}{(7-7)!7!}(0.5)^7(1-0.5)^{7-7}\)Evaluating, you get:
\(P(X\ge5)\approx0.2266\)(c) You must find the probability that in the next 7 dinners Joe prepares, less than 3 of them will burn. Therefore, you need to set up a Sum for:
\(\begin{gathered} x=0 \\ x=1 \\ x=2 \end{gathered}\)As follows:
\(P(X<3)=\frac{7!}{(7-0)!0!}(0.5)^0(1-0.5)^{7-0}+\frac{7!}{(7-1)!1!}(0.5)^1(1-0.5)^{7-1}+\frac{7!}{(7-2)!2!}(0.5)^2(1-0.5)^{7-2}\)Evaluating, you get:
\(P(X<3)\approx0.2266\)Hence, the answers are:
(a)
\(0.2734\)(b)
\(0.2266\)(c)
\(0.2266\)Three partners share a business. Max owns 3 8 , Sherry owns 2 5 , and Duane owns the rest. If the profits this year are $350,000, how much does each partner receive (in $)?
Answers
answer:
Max =$131,250
Sherry=$140,000
Duane=$78,750
Step-by-step explanation:
Max will receive 3/8 ×$350,000=$131,250
Sherry will receive 2/5 × $350,000=$140,000
Duane will receive $350,000-$(131,250+140,000)
$350,000-$271,250=$78,750.
Doug drew two identical triangles. He wants to prove the converse of the Pythagorean Theorem by using both triangles. The first triangle has side lengths of 12 cm, 16 cm, and 20 cm, such that 122 + 162 = 202. Using the converse of the Pythagorean Theorem, enter the length of the side opposite the 90° angle of the second triangle.______cm
Answers
Answer:
Answer is explained in the explanation section
Step-by-step explanation:
Solution:
Converse of the pythagorean theorem helps us to check whether a triangle is a right triangle or not. Converse of the pythagorean theorem is simply the opposite of the pythagoren theorem. Pythagorean theorem states that, if triangle is right triangle, then \(a^{2} + b^{2} = c^{2}\). On the other hand, Converse of the Pythagorean theorem states that, if \(a^{2} + b^{2} = c^{2}\), then triangle is a right triangle.
Pythagorean theorem = \(c^{2} = a^{2} + b^{2}\)
Converse of the pythagorean theorem = \(a^{2} + b^{2} ? c^{2}\)
First of all let's check the first triangle is right triangle or not.
a = 12
b= 16
c= 20
So,
\(a^{2} + b^{2} = c^{2}\).
144 + 256 = 400
400 = 400
Yes, 1st triangle is no doubt a right triangle. On the other hand, we are given that 2nd triangle = right triangle as we are given the 90 degree angle already. Here, we know that triangle is a right triangle
hence, \(a^{2} + b^{2} = c^{2}\). will surely be there.
Now, we have find out the side opposite to the 90 degrees angle, which is c.
we also know that, right triangles sides follow the pattern of 3x,4x and 5x
Since, c is the longest side.
Hence, c= 5x
A house has increased in value by 35% since it was purchased. If the current value is $297,000, what was the value when it was purchased?
Answers
Answer:
Answer:
$260,000
Step-by-step explanation:
Explanation:
Given the problem above, we solve for original value
Hence, in this case, we are given
percentage (35%) and the New Value ($351,000).
We can substitute this into the formula and solve for X
Let X be the original price, Hence, X = 100%
Therefore, $351000 = 135%
Divide both sides by 135
351000÷ 135 = 135÷135
2600 = 1%
Multiply both sides by 100
2600 * 100 = 1% * 100
$260000 = 100% = X
Hence, final answer is $260000
Question 3 (Mandatory) (10 points)
Simplify
(2/3a - 5) - (1/3a + 3)
*Please show your work so I can’t understand better thank you*
Answers
Answer:
1/3a - 8
Step-by-step explanation:
Distribute negative sign:
2/3a - 5 + -1 (1/3a + 3)
2/3a + -5 + -1 (1/3a) + (-1)(3)
2/3a + -5 + -1/3a + -3
Combine like terms:
2/3a + -5 + -1/3a + -3
(2/3a + -1/3a) + (-5 + -3)
= 1/3a - 8
How long does it take the kangaroo to travel 5 km
Answers
Answer:
Time taken by kangaroo to travel 5 km = 4.27 minutes.
Step-by-step explanation:
Speed of kangaroo is 44 mph.
Speed of kangaroo = 44 mph = 44 x 1.6 = 70.4 kmph = 19.5 m/s
We need to find how much time it takes to travel 5 km
Distance traveled = 5 km = 5000 m
We have
Distance traveled = Speed x Time taken
5000 = 19.5 x Time taken
Time taken = 256.41 seconds
Time taken = 4.27 minutes.
Answer:7.5
Step-by-step explanation:
What is the solution to the equation 4x + 2(x − 2) = 4x + x − 12? (1 point)
Question 13 options:
1)
−8
2)
−1
3)
1
4)
8
Answers
Answer:
It's -8
Step-by-step explanation:
DISTRIBUTE :
4x + 2( x - 2 ) = 4x + x - 12
4x + 2x - 4 = 4x + x - 12
COMBINE LIKE TERMS :
4x + 2x - 4 = 4x + x - 12
6x - 4 = 4x + x - 12
COMBINE LIKE TERMS :
6x - 4 = 4x + x - 12
6x - 4 = 5x - 12
ADD 4 TO BOTH SIDES :
6x - 4 = 5x - 12
6x - 4 + 4 = 5x - 12 + 4
ADD THE NUMBERS/ SIMPLIFY :
6x = 5x - 8
SUBTRACT 5x FROM BOTH SIDES :
6x = 5x - 8
6x - 5x = 5x - 8 - 5x
SIMPLIFY :
x = -8
Nine less than the product of a number n and 1/6 is no more than 92

Answers
Answer:
Please help im on that 2dd
Step-by-step explanation:
dddd