Graph the inequality x>2
on the number line.
+
-2
+
-1
+
0
+
1
+
2.
+
3
+
7
+
8
4
5
9
10
Answers
Answer:
no problem :) have a nice day
Step-by-step explanation:

Related Questions
Perform the operation and simplify please &thank you!

Answers
Simplify the given expression as follows:
\(\cfrac{4x+1}{x^2-4} -\cfrac{3}{x-2} =\)\(\cfrac{4x+1}{(x+2)(x-2)} -\cfrac{3}{x-2} =\) Identity for difference of squares\(\cfrac{4x+1}{(x+2)(x-2)} -\cfrac{3(x+2)}{(x+2)(x-2)} =\) Common denominator\(\cfrac{4x+1-3(x+2)}{(x+2)(x-2)} =\) Simplify numerator\(\cfrac{4x+1-3x-6}{(x+2)(x-2)} =\) \(\cfrac{x-5}{(x+2)(x-2)} =\)\(\cfrac{x-5}{x^2-4} =\)\(\cfrac{x+(-5)}{x^2+(-4)}\)The missing numbers are - 5 and - 4.
The volume inside of a sphere is V=4πr33 where r is the radius of the sphere. Your group has been asked to rearrange the formula so that it is rewritten to solve for r. Below are various solutions that your group-mates have arrived at. Select the correct one A) r=3V4π−−−√ B) r=3V4π−−−√3 C) r=3V√34π D) r=4V3π−−−√3
Answers
Answer:
Step-by-step explanation:5
Can some one help me plzzz will give brainiest

Answers
Answer:
3rd choice Hoped this helped :_)
Step-by-step explanation:
Brainliest plz ^
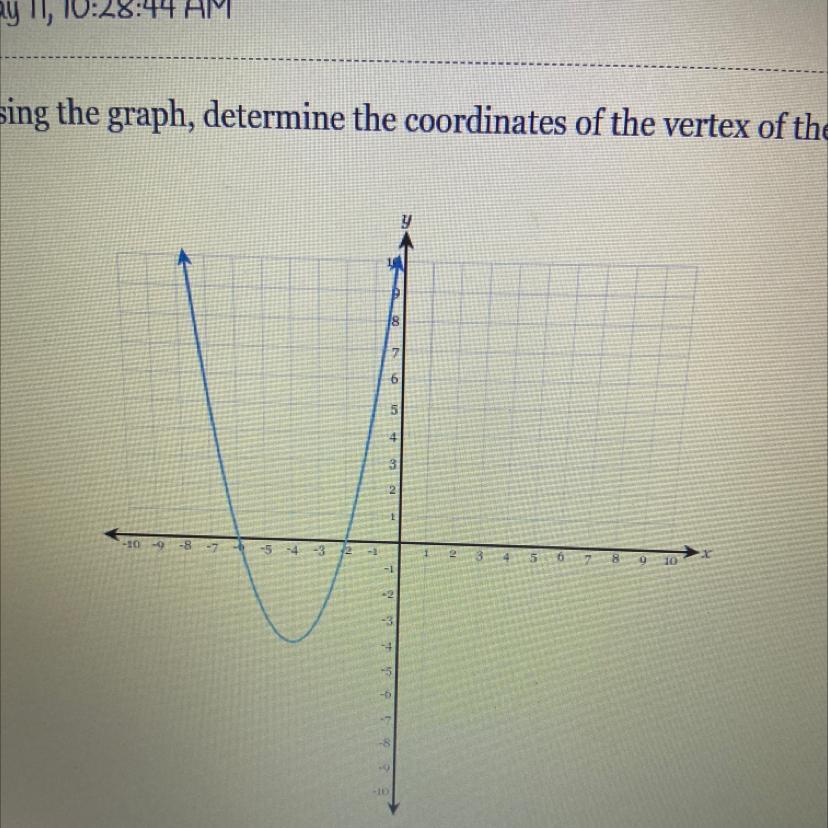
Using the graph, determine the coordinates of the vertex of the parabola.
Answers
Answer:
(-4,-4)
Step-by-step explanation:
You can see the vertex from the graph
Answer:
(-4,-4)
Step-by-step explanation:
Vertex is the the point in which the graph originates from
100 POINTS IF U GET THIS RIGHT!

Answers
Take two points
(-3,0)(0,-3)\(\\ \sf\longmapsto m=\dfrac{-3-0}{0+3}=\dfrac{-3}{3}=-1\)
Equation of line in slope intercept form
\(\\ \sf\longmapsto y=mx+b\)
\(\\ \sf\longmapsto y=-x-3\)
the
blueprint specification for a machined part calls for its
thicknessto be 1.485 in. with a tolerance of 0.010in. find the
limit dimensions of the part.
Answers
The limit dimensions of the part are **1.475 in.** to **1.495 in.**
The blueprint specification states that the thickness of the machined part should be 1.485 in. with a tolerance of 0.010 in. Tolerance refers to the acceptable deviation from the specified dimension. In this case, the tolerance is ±0.010 in., which means the actual thickness can vary by up to 0.010 in. in either direction.
To find the limit dimensions, we need to consider both the upper and lower limits. The lower limit is calculated by subtracting the tolerance from the specified dimension, while the upper limit is obtained by adding the tolerance to the specified dimension.
Lower limit: 1.485 in. - 0.010 in. = 1.475 in.
Upper limit: 1.485 in. + 0.010 in. = 1.495 in.
Therefore, the limit dimensions of the part are 1.475 in. to 1.495 in. These limits ensure that the part is within the acceptable range of thickness specified by the blueprint.
Learn more about limit dimensions
brainly.com/question/16845597
#SPJ11
A video game store allows customers to rent games for $4.75 each. Customers can also buy a membership for $54 each year, and video games would then only cost $2.50 each to rent. Write and solve an equation to find the number of video games a customer would have to rent in a year in order for the two options to be equal.
Answers
Answer:
24
Step-by-step explanation:
Cost of membership + game = 2.50x + 54
Cost of just games = 4.75x
The catch is, how do we make up the 54 dollars?
So equate the 2 costs
4.75x = 2.50x + 54 Subtract 2.50
4.75x - 2.50x = 54 Combine
2.25x = 54 Divide by 2.25
x = 54/2.25
x = 24
That means that 24 is the break even point.
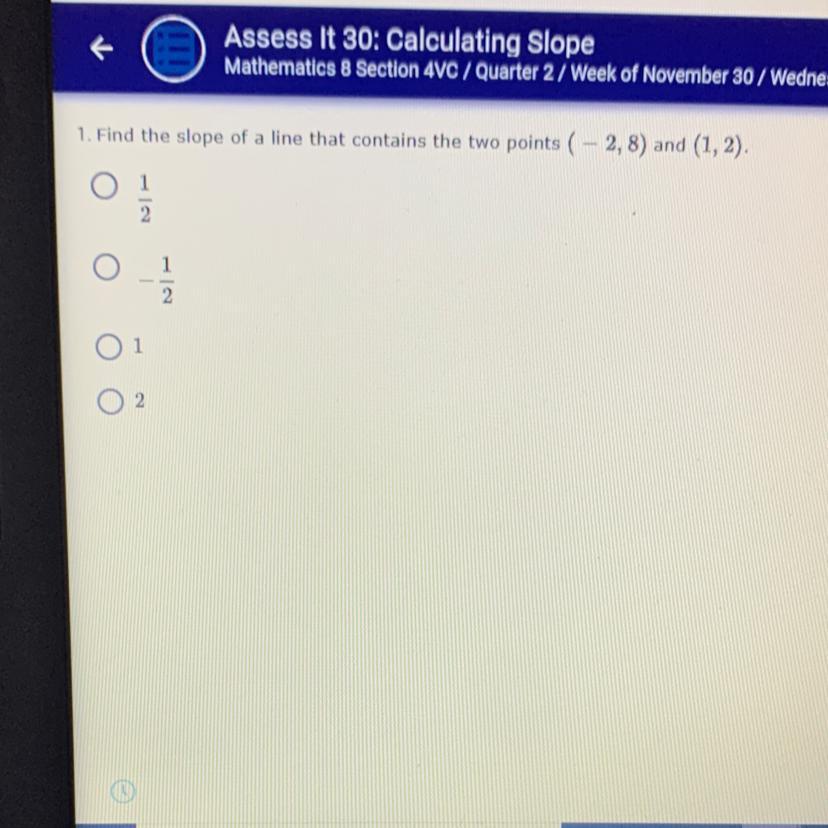
URGENT NEED OF HELP PLEASE ILL GIVE BRAINLEST
Answers
Answer:
umm.. I think the answer choices are wrong because the slope is -2.
y = mx + b
y = (slope)x + (y-intercept)
y = -2x + 4
and i have proof!
Step-by-step explanation:

15 POINTs_ NEED ASAP!
Tell whether the following statements are true or false, explain the reasoning.

Answers
Answer:
Step-by-step explanation:
1 TRUE
A number is always 100% Anyting bigger than 100% is going to be a bigger number
Anything smaller than 100% is a smaller number
2FALSE 5/100 = 0.05 and NOT 0.5
0.5% is the same as thalf of 100% = 50%
50/100 = 5/10 = 0.5
If two lines are perpendicular to each other, do they lie in the same plane?
Answers
Select the correct answer. If the number of equally likely sample outcomes of a single stage of an experiment is 4, what is the total number of elements in the sample space if the experiment has 3 stages? A. 16 B. 12 C. 64 D. 81
Answers
Answer:
The total number of elements in the sample space of the experiment for 3 stages = 64 (C)
Step-by-step explanation:
The number of equally likely sample outcomes of the single stage experiment = 4
For n number of stages, the total number of elements in the sample space = (outcome of a single stage)^n
This is = 4^n
To determine the total number of elements in the sample space if the experiment has 3 stages, we would multiply the outcome of one experiment three times.
Where n = 3
The total number of elements in the sample space of the experiment for 3 stages = 4³
= 4×4×4 = 64
The total number of elements in the sample space of the experiment for 3 stages = 64 (C)
Answer:
The answer is c. 64. I did the quiz and i got it right
Step-by-step explanation:
Please help me:) I don’t know what to do

Answers
Answer:
8 family members. Average of 2.6 fish per person.
Step-by-step explanation:
How many family members caught fish? Count only those members who caught at least 1 fish (that's all of them, because nobody caught 0 fish!).
3 + 1 + 0 + 4 = 8 family members.
Average number of fish caught per person. This is the total number of fish caught divided by the total number of people.
This is a little bit tricky because, for example, 4 people caught 4 fish, making 4 x 4 = 16 fish caught.
Multiply number of fish (column 1) by the number of people (column 2):
1 x 3 + 2 x 1 + 3 x 0 + 4 x 4 = 3 + 2 + 0 + 16 = 21 fish caught.
21 fish. 8 people. On average, that is 21 / 8 = 2.625 which rounds to 2.6 fish per person.
Hint: the word "per" means divide, so "fish per person" tells you to divide the total number of fish by the total number of people.
Good Luck!
which of the following samples could constitute a discrete random variable? i. total number of points score in a football game. ii. height of the ocean's tide at a given location. iii. number of near collisions of aircraft in a year.
Answers
The sample that could constitute a discrete random variable is the number of near collisions of aircraft in a year.
This is because it is a countable, finite number and not a continuous measurement like the height of the ocean's tide. The total number of points scored in a football game could also be considered a discrete random variable because it is a countable, finite number. However, the height of the ocean's tide is a continuous measurement and cannot be counted as a discrete random variable.
The sample that could constitute a discrete random variable is: i. total number of points scored in a football game.
A discrete random variable represents a countable number of distinct values or outcomes. In this case, the total number of points scored in a football game can be counted and listed, making it a discrete random variable.
On the other hand, the height of the ocean's tide at a given location (ii) is a continuous random variable, as it can take any value within a given range, and the number of near collisions of aircraft in a year (iii) could also be considered as a discrete random variable, but it's not one of the options in your question.
Visit here to learn more about aircraft:
brainly.com/question/28246952
#SPJ11
T/F: the coefficient of determination measures the variation in the dependent variable that is explained by the regression model.
Answers
True. The coefficient of determination (R²) measures the proportion of the variation in the dependent variable that is explained by the regression model.
In statistics, the coefficient of determination (denoted R² or r² and pronounced "R squared") is used in the context of statistical models whose main purpose is either the prediction of future results or the testing of hypotheses, on the basis of other related information.
It is also known as the multiple correlation coefficient or the multiple determination coefficient. It is the proportion of the variance in the dependent variable that is predictable from the independent variable(s).
In a simple regression model, this is the square of the correlation between the dependent variable and the single independent variable.
Hence, the given statement is True.
To know more about the "regression model": https://brainly.com/question/25987747
#SPJ11
Factor pair are two factors that can be multiplied together to get a product
a. true
b. false
Answers
Answer:
a. true
Step-by-step explanation:
Factor pair are two factors that can be multiplied together to get a product
TRUE
Answer:
I would say True :)
Step-by-step explanation:
Hope this helps!!! (。 ◕‿‿◕。)
ASAP Distribute 6(2+9x²)
Answers
Answer:
Step-by-step explanation:
(6*2) + (6*9x2)
12 + 54x2
Let Z be the standard normal variable with expected value 0 and variance (standard deviation) 1. According to the Chebyshev inequality, P(\Z\ GE 0.95) LE pi your answer to six decimal places) In fact, P(\Z\ GE 0.95) (give your answer to four decimal places)
Answers
According to the Chebyshev inequality, the probability of Z being greater than or equal to 0.95 is less than or equal to pi. The actual probability is approximately 0.1587.
According to Chebyshev's inequality, for any random variable X with expected value E(X) and standard deviation sigma, the probability of X deviating from its expected value by more than k standard deviations is at most 1/k^2. Mathematically,
P(|X - E(X)| >= k * sigma) <= 1/k^2
In this case, we have a standard normal variable Z with E(Z) = 0 and sigma = 1. We want to find the probability of Z being greater than or equal to 0.95, which is equivalent to finding P(Z >= 0.95).
We can use Chebyshev's inequality with k = 2 to bound this probability as follows:
P(Z >= 0.95) = P(Z - 0 >= 0.95 - 0) = P(|Z - E(Z)| >= 0.95) <= 1/2^2 = 1/4
So, we have P(Z >= 0.95) <= 1/4. However, this is a very conservative bound and we can get a better estimate of the probability by using the standard normal distribution table or a calculator.
Using a calculator or a software, we get P(Z >= 0.95) = 0.1587 (rounded to four decimal places), which is much smaller than the upper bound of 1/4 given by Chebyshev's inequality.
Therefore, we can conclude that P(Z >= 0.95) <= pi (approximately 3.1416) according to Chebyshev's inequality, but the actual probability is approximately 0.1587.
For more questions like Probability click the link below:
https://brainly.com/question/30034780
#SPJ11
PLEASE HELP!! :))
System A:
4x + 16y = 12
x +2y = -9
System B:
4x + 16y = 12
x + 4y = 3
1) How can we get System B from System A?
Choose 1 answer:
A. Replace one equation with a multiple of the other equation
B. Replace one equation with a multiple of itself
C. Swap the left-hand sides of both equations
D. Swap the order of the equations
2) Based on the previous answer, are the systems equivalent? In other words, do they have the same solution?
Choose 1 answer:
A. Yes
B. No
Answers
To get System B from System A, you can replace one equation with a multiple of the other equation. Specifically, you can multiply the second equation of System A by 2 and then replace the first equation with the result. So the correct answer is A.
Since we obtained System B by performing a valid operation on System A, the two systems are equivalent and have the same solution. So the correct answer is A. Yes, they have the same solution
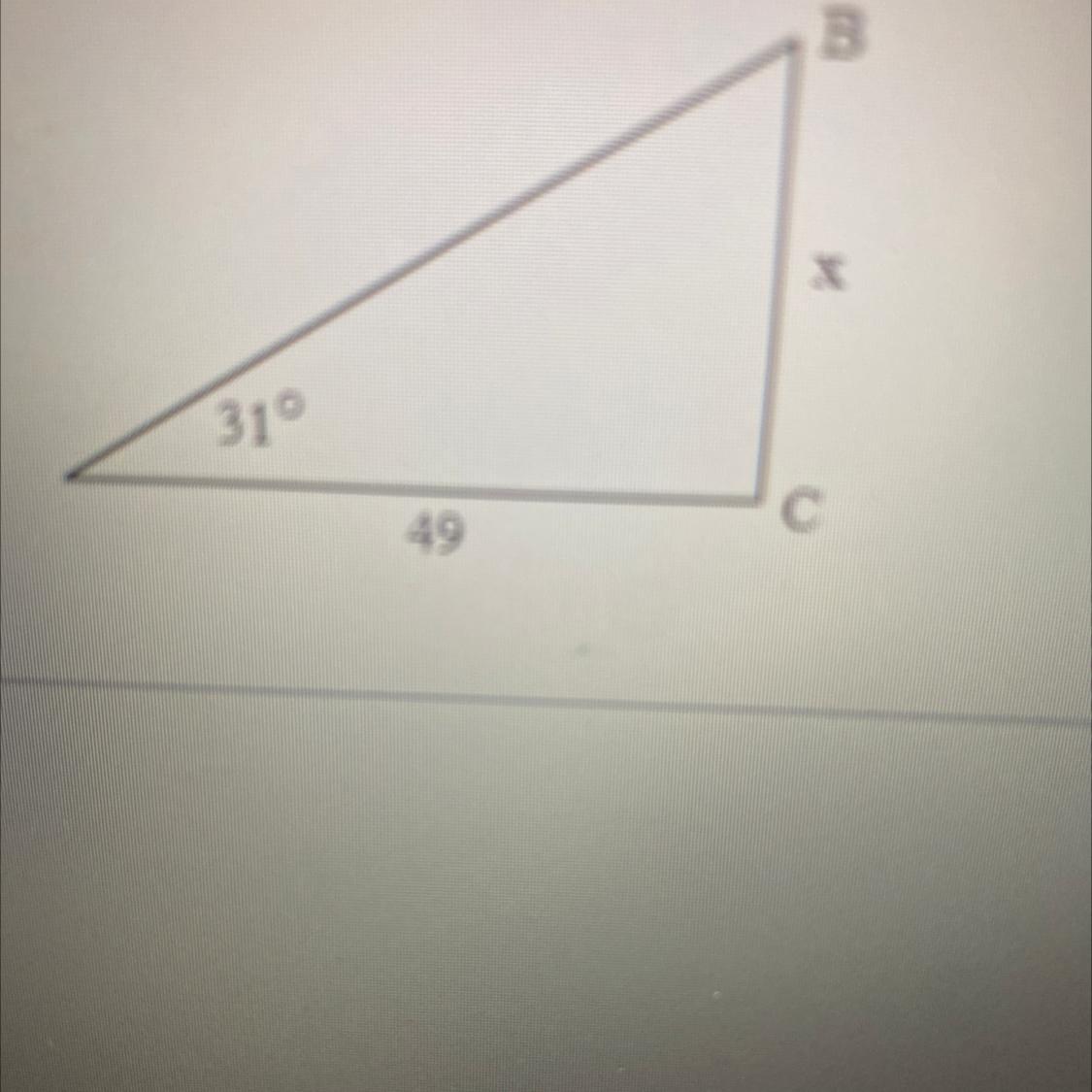
PLEASE HELPP
Solve for x
Answers
Answer:
x = 29.44
Step-by-step explanation:
\(tan31^{o} =\frac{x}{49}\)
\(x=49tan31^{o}\)
\(x=29.44\)
Hope this helps
Hopefully this helps
A group of people were asked how many people live in their household. What percent of these people have exactly 2 people in their household?
Answers
Answer:
16%
Step-by-step explanation:
Given
\(\begin{array}{cccccc}{Size & {1} & {2} & {3} & {4} & {5} \ \\ {f} & {3} & {4} & {6} & {7} & {5} \ \end{array}\)
Required
The percentage of household with 2 people
First, calculate the total frequency
\(Total = 3 + 4 +6+7+5\)
\(Total = 25\)
The frequency of household with 2 people is:
\(f(2) = 4\)
So, the percentage is calculated as:
\(\% =\frac{f(2)}{Total} * 100\%\)
\(\% =\frac{4}{25} * 100\%\)
\(\% =\frac{400}{25}\%\)
\(\% =16\%\)
Write an equation of the line that passes through (3, 7) and is parallel to the line shown. (1, 4) (- 2, - 2)

Answers
Answer:
y=2x+1.
Step-by-step explanation:
You first need to find the slope of the line already graphed. -2 to 1 would be three units to the right, and -2 to 4 would be six units up. You would use the equation (y2-y1)/(x2-x1), where x1 and y1 would be the x and y values of the first coordinate of the graphed line, and x2 and y2 would be the second coordinate. This would be 6/3, which can be simplified to 2/1, which can be simplified to 2, which would mean the slope of the given line would be 2, as well as the parallel line. Now, you could use a pretty complicated equation to find the y-intercept of the line you need to graph, but I would recommend using the slope to find it. Since the given point is (3, 7), you would need to go to the left, meaning you would reverse the slope until you reach the y-axis, so you would use -2 as the slope. 3*-2=-6, and 7-6=1, so the y-intercept would be 1. The answer would be y=2x+1. Hope this helps.
6 cars 4 people in each car HELP I HAVE 3 minutes
Answers
Answer:
Here we have 6 cars.
And we know that there are 4 people in each car.
The question is incomplete, I assume that we want to find the total number of people in the 6 cars.
So, again, there are 6 cars, and 4 people in each one.
Then we have 6 times 4 people.
This is equal to the product between 6 and 4, which is:
6*4 = 24
There is a total of 24 people in the 6 cars.
Show All Your Work! Find the exact area of the surface obtained by rotating the curve about the x-axis: y = √5-x, 3 ≤x≤5
Answers
A = 2π ∫ [3, 5] √((5 - x)(1 + (1/4) * (5 - x)^(-1))) dx. This integral can be evaluated using standard techniques, such as substitution or expanding the exon.
To find the exact area of the surface obtained by rotating the curve y = √(5 - x) about the x-axis over the interval 3 ≤ x ≤ 5, we can use the formula for the surface area of revolution. The second paragraph will provide a step-by-step explanation of the calculation.
The formula for the surface area of revolution about the x-axis is given by: A = 2π ∫ [a, b] y * √(1 + (dy/dx)²) dx,
where a and b are the limits of integration.
In this case, the limits of integration are 3 and 5, as given in the problem statement.
First, we need to calculate dy/dx, the derivative of y with respect to x. Taking the derivative of y = √(5 - x), we have:
dy/dx = (-1/2) * (5 - x)^(-1/2) * (-1) = (1/2) * (5 - x)^(-1/2).
Now we substitute the values into the formula for surface area:
A = 2π ∫ [3, 5] √(5 - x) * √(1 + ((1/2) * (5 - x)^(-1/2))²) dx.
Simplifying the expression inside the integral, we have:
A = 2π ∫ [3, 5] √(5 - x) * √(1 + (1/4) * (5 - x)^(-1)) dx.
Next, we can combine the square roots:
A = 2π ∫ [3, 5] √((5 - x)(1 + (1/4) * (5 - x)^(-1))) dx.
This integral can be evaluated using standard techniques, such as substitution or expanding the exon. Apressifter performing the integration, we will have the exact value of the surface area of the rotated curve about the x-axis over the given interval.
Learn more about interval here: brainly.com/question/11051767
#SPJ11
What is the formula in statistic for two cards drawn at random without replacement if both cards are green?
Answers
The formula in statistic to calculate cards drawn at random without replacement shows both the cards are green is given by,
P(both cards are green)
= (number of green cards / total number of cards) × ((number of green cards - 1) / (total number of cards - 1))
The formula in statistics for calculating the probability of drawing two cards at random without replacement,
Both cards are green, depends on the total number of cards and the number of green cards in the deck.
Let us consider there are N total cards in the deck.
And k of them are green.
Probability of drawing two green cards without replacement,
use the following formula,
P(both cards are green)
= (number of green cards / total number of cards) × ((number of green cards - 1) / (total number of cards - 1))
⇒ P(two green cards) = (k/N) x ((k-1)/(N-1))
First term in the formula represents the probability of drawing a green card on the first draw.
Second term represents the probability of drawing a green card on the second draw.
First card was green and hasn't been replaced.
Assumes that each card in the deck is equally likely to be drawn.
And that the two draws are independent of each other .
For example,
A deck of 52 cards,
And there are 13 green cards in the deck (4 of each suit).
The probability of drawing two green cards without replacement would be,
P(two green cards)
= (13/52) x ((12/51))
= 0.0588
Therefore, the probability of drawing two green cards without replacement is approximately 0.0588 or 5.88%.
Learn more about cards here
brainly.com/question/4519526
#SPJ4
The above question is incomplete, the complete question is:
Two cards are drawn at random from a deck of 52 cards of four different color without replacement. What is the formula in statistic for two cards drawn at random without replacement if both cards are green ?
for an experiment involving 2 levels of factor a and 3 levels of factor b with a sample of 5 in each treatment condition, what is the value for dfwithin?
Answers
The value for df within in an experiment with two levels of factor a and three levels of factor b and five samples for each treatment condition is between 3.
Explain the term levels of factor?In a two-way ANOVA, the 2 separate variables are known as factors. Two variables, or factors, are supposed to influence the dependent variable. There will be two or even more levels inside each factor, and there are one less degrees of freedom per factor than there are levels.Let n1 represent factor A's level of freedom.
Let n2 represent factor B's degree of freedom.
If factor A has five levels, then n1 = 2.
If Factor B has seven levels, then n2 = 3.
The formula is used to express how the degrees of freedom interact;
df = (n1 - 1)+(n2 - 1) (n2 - 1)
df = n1 -1 + n2- 1
df = n1 + n2 -2
Replace n1 and n2 to obtain df;
df = 2 + 3 - 2
df = 3
Thus, the value for df within in an experiment with two levels of factor a and three levels of factor b and five samples for each treatment condition is 3.
To know more about the levels of factor, here
https://brainly.com/question/19052897
#SPJ4
solve the inequality -2z-3<5. what is the value of z?
Answers
Hey there!
The answer to your question is z > -4
We can solve this like it is an equation, with one exception. When you divide or multiply by a negative number, in an inequality, you have to flip the inequality sign.
-2z - 3 < 5 add 3 to both sides
-2z < 8 divide both sides by -2, and flip the inequality sign
z > -4
Good luck! Hope it helps, and have a great day!
Answer:
The answer is z > -4
but a line down were is the (>)
I ready!
holpe it help
For a nack Sameer ate a plum with 23 calories and sereval strawberries with 4 calories each if the total number of calories in sameer snak was 56 how many strawberries did he eat
Answers
Answer: 5.75
Step-by-step explanation:
56-23=23 23 divided by 4 = 5.75:)
CAN SOMEONE PLS HELP THIS IS URGENT

Answers
Answer:
a
Step-by-step explanation:
Answer: C 72=9÷1/8
I hope this helps:
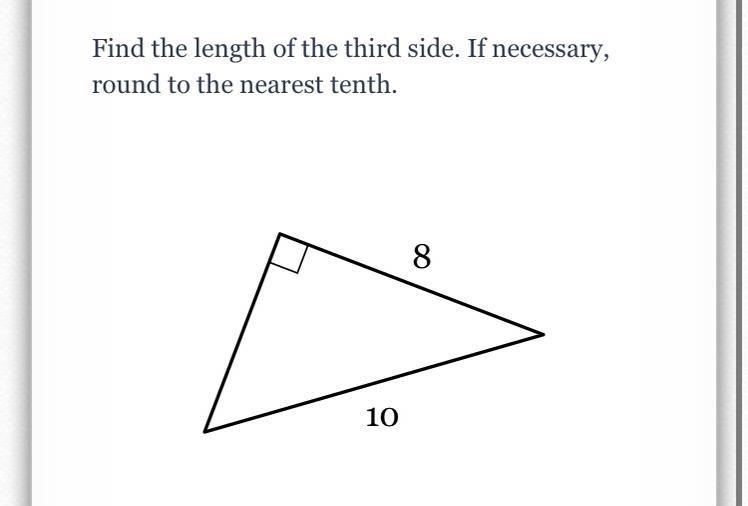
Someone help please, picture attached
Answers
Answer:
6
Step-by-step explanation:
x² + 8² = 10²
x² + 64 = 100
x² = 36
x = 6
when you make the circle bigger or smaller which number of the standard equation for a circle centered at the orgin changes
Answers
To dilate a circle by a determined scale factor k you have to work on the standard equation of the circle
\(x^2+y^2=r^2\)You have to multiply the radius by the squared scale factor:
\(x^2+y^2=k^2r^2\)So, if do example you want to dilate a circle by a scale factor 3, you have to multiply the radius by the square of 3
\(\begin{gathered} k=3 \\ 3^2=9 \end{gathered}\)The formula of the circle dilated by k=3 is
\(x^2+y^2=9r^2\)