I need to know the percentage of drivers who are at least 45. Using the table in the picture.

Answers
The percentage of drivers who are at least 45 is 62%
How to determine the percentage of drivers who are at least 45.From the question, we have the following parameters that can be used in our computation:
The table of values
From the table, we have
Age 45 = 62 percentile
When represented properly
So, we have
Age 45 = 62%
This means that the percentage of drivers who are at least 45 is 62%
Read more abot percentage at
https://brainly.com/question/24877689
#SPJ1
Related Questions
A polygon has vertices at (–5, 3), (–1, 3), (1, 0), and (–3, 0). Which represents a geometric translation of the given polygon 4 units to the right and 5 units down?
Answers
The geometric translation of the given polygon 4 units to the right and 5 units down is; (-9, -2), (-5, -2), (-3, -5) and (-7, -5)
How to carry out transformation rule?
The four important rules of transformation are;
Vertical transformation.Horizontal transformation.Stretched transformation.Compressed transformationNow, the transformation rule of moving a units to the right is;
(x, y) = (x - 5)
Thus, moving the polygon by 4 units to the right is;
(–5 - 4, 3), (–1 - 4, 3), (1 - 4, 0), and (–3 - 4, 0)
= (-9, 3), (-5, 3), (-3, 0) and (-7, 0)
Now, when we translate it by 5 units down, we will have;
(-9, 3 - 5), (-5, 3 - 5), (-3, 0 - 5) and (-7, 0 - 5)
= (-9, -2), (-5, -2), (-3, -5) and (-7, -5)
Read more about Transformation rule at; https://brainly.com/question/8987411
#SPJ1
Answer:
Step-by-step explanation:
its b
PLEASE HELP QUICKLY AS POSSIBLE THANK YOU :)

Answers
Answer:
$40.52
Step-by-step explanation:
You add the amount of all the t-shirts that Mike bought and subtract it from 100.
The base of the triangle is 5 inches. The length of the rectangle is 15 inches. The height of the triangle is 10 inches. Find the surface area
Answers
Answer:
275 square inches
Step-by-step explanation:
Here we have to give us various measurements, but we do not know to which figure it corresponds since you do not attach it, but I have found an image where they asked the same questions and it makes sense that it is the question, the attached one.
We have that the rectangle is 15 inches long and the width corresponds to the same as the base of the triangle, that is, 5 inches, therefore, the area of the rectangle would be:
A = l * w
A = 15 * 5
A = 75
75 in ^ 2 but how are 3 rectangles would be:
75 * 3 = 225
225 in ^ 2 would be the area of the 3 rectangles, it would be necessary to add the area of the two triangles that would be:
A = b * h / 2
replacing:
A = 5 * 10/2
A = 25
25 in ^ 2 for the triangle, but being 2, they would be 50 ^ 2, now in total they would be:
225 + 50 = 275
In other words, the surface area of the figures is 275 square inches

Find the value of x that makes the equation true:
8x = 8
x = 1
x = 0
x = 3
x = 2
Answers
Answer: x=1
Step-by-step explanation: Divide both sides by 8.
Answer:
x=1
Step-by-step explanation:
i had this question
Dogs or cats which one is better???
Answers
Answer:
dogs
Step-by-step explanation:
they are more freindly
Answer:
dogs
Step-by-step explanation:
i just had to take a test and one of the questions was to write an essay about dogs or cats being better so i searched it up and it said dogs
Find the measure of angle T for the kite below
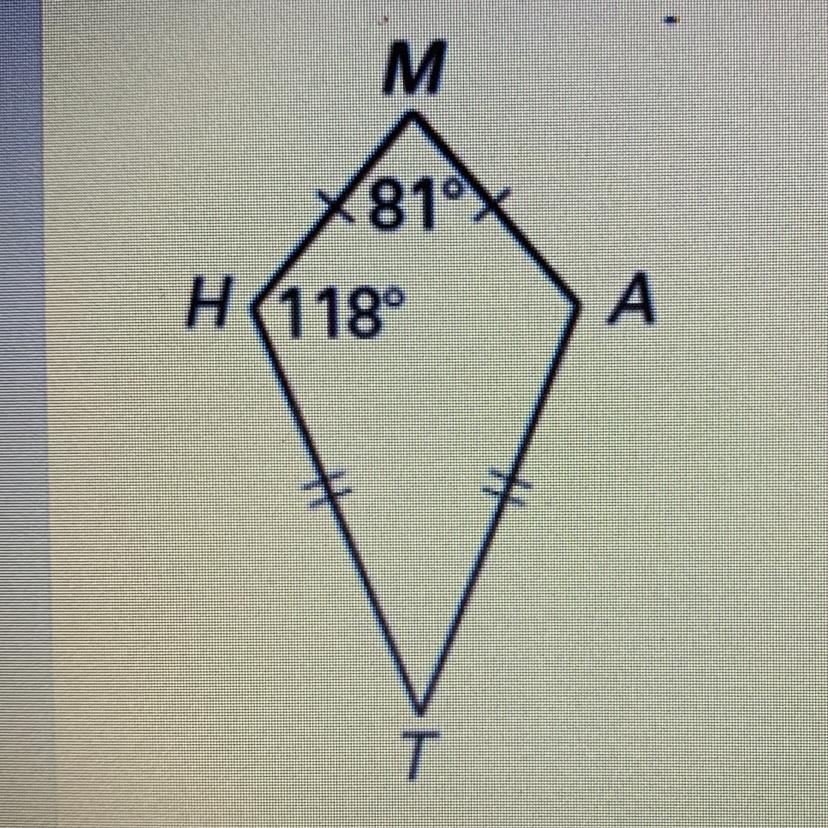
Answers
Answer:
Angle T = 43°
Step-by-step explanation:
118+118+81 = 317
360-317 = 43
Using exactly four 4's and any operation or symbols [+, -, *, /, (), x to the power of __], write an expression to equal each of the following:
1 = ________________ 4 = _______________ 7 = ________________
2 = ________________ 5 = _______________ 8 = ________________
3 = ________________ 6 = _______________ 9 = ________________
Answers
Answer:
1→ (4/4) / (4/4) = 1/1 = 1
2→ (4*4) / (4+4)= 16/8 = 2
3→ (4+4+4)/4 = 12/4 = 3
4→ (4-4)*4 + 4= 0*4 + 4= 4
5→ (4*4 +4) /4 = 20/4 =5
6→ 4+(4+4)/4 = 4+ 8/4 = 4+2 =6
7→ 4+4 -4/4 = 8-1=7
8→ 4+4+4-4=12-4=8
9→ 4+4 + (4/4)= 8+1 =9
Step-by-step explanation:
how to rewrite 9/10 and 23/25 so they have common denominators
Answers
Find the value of win the isosceles triangle shown below.
8
8
7
8
LA
Choose 1 answer

Answers
Answer:
x=6.93
Step-by-step explanation:
use the Pythagorean theorem
8^2=(0.5 x 8)^2+x^2
64=16+x^2
x^2=48
x=6.93
Answer:x= Square root 48
Step-by-step explanation:
Please help me with this.

Answers
Here are the correct matches to the expressions to their solutions.
The GCF of 28 and 60 is 4.
(-3/8)+(-5/8) = -4/4 = -1.
-1/6 DIVIDED BY 1/2 = -1/6 X 2 = -1/3.
The solution of 0.5 x = -1 is x = -2.
The solution of 1/2 m = 0 is m = 0.
-4 + 5/3 = -11/3.
-2 1/3 - 4 2/3 = -10/3.
4 is not a solution of -4 < x.
1. The GCF of 28 and 60 is 4.
The greatest common factor (GCF) of two numbers is the largest number that is a factor of both numbers. To find the GCF of 28 and 60, we can factor each number completely:
28 = 2 x 2 x 7
60 = 2 x 2 x 3 x 5
The factors that are common to both numbers are 2 and 2. The GCF of 28 and 60 is 2 x 2 = 4.
2. (-3/8)+(-5/8) = -1.
To add two fractions, we need to have a common denominator. The common denominator of 8/8 and 5/8 is 8. So, (-3/8)+(-5/8) = (-3 + (-5))/8 = -8/8 = -1.
3. -1/6 DIVIDED BY 1/2 = -1/3.
To divide by a fraction, we can multiply by the reciprocal of the fraction. The reciprocal of 1/2 is 2/1. So, -1/6 DIVIDED BY 1/2 = -1/6 x 2/1 = -2/6 = -1/3.
4. The solution of 0.5 x = -1 is x = -2.
To solve an equation, we can isolate the variable on one side of the equation and then solve for the variable. In this case, we can isolate x by dividing both sides of the equation by 0.5. This gives us x = -1 / 0.5 = -2.
5. The solution of 1 m = 0 is m = 0.
To solve an equation, we can isolate the variable on one side of the equation and then solve for the variable. In this case, we can isolate m by dividing both sides of the equation by 1. This gives us m = 0 / 1 = 0.
6. -4 + 5/3 = -11/3.
To add a fraction and a whole number, we can convert the whole number to a fraction with the same denominator as the fraction. In this case, we can convert -4 to -4/3. So, -4 + 5/3 = -4/3 + 5/3 = -11/3.
7. -2 1/3 - 4 2/3 = -10/3.
To subtract two fractions, we need to have a common denominator. The common denominator of 1/3 and 2/3 is 3. So, -2 1/3 - 4 2/3 = (-2 + (-4))/3 = -6/3 = -10/3.
8. 4 is not a solution of -4 < x.
The inequality -4 < x means that x must be greater than -4. The number 4 is not greater than -4, so it is not a solution of the inequality.
For more such questions on GCF
https://brainly.com/question/902408
#SPJ8
Help me I’ll give you stars

Answers
Answer:answer choice 2
Step-by-step explanation:
The amount that households pay service providers for access to the Internet varies quite a bit, but the mean monthly fee is $50 and the standard deviation is $20. The distribution is not Normal: many house- holds pay a low rate as part of a bundle with phone or television service, but some pay much more for Inter- net only or for faster connections.
A sample survey asks an SRS of 50 households with Internet access how much they pay. Let x be the mean amount paid.
(a) Explain why you can't determine the probability that the amount a randomly selected household pays for access to the Internet exceeds $55.
(b) What are the mean and standard deviation of the sampling distribution of ?
(c) What is the shape of the sampling distribution of x? Justify your answer.
(d) Find the probability that the average fee paid by the sample of households exceeds $55. television service, but some pay much more for Inter- net only or for faster connections.
Answers
Answer:
(a) See Explanation
(b) \(\bar x =50\) and \(\sigma_x = 0.8944\)
(c) The shape is normal
(d) \(P(\bar x > 55) = 0\)
Step-by-step explanation:
Given
\(\mu = \$50\) -- mean
\(\sigma = \$20\) --- standard deviation
\(n=500\) --- sample size
Solving (a): The reason we can't determine the probability that an amount to access internet by a household will exceed $55.
The question says that a lot of households pay low rates, but the percentage of the households in this category is not given. This means that it is impossible to determine the shape of the distribution.
Hence, the probability cannot be calculated.
Solving (b): Sample mean and Sample standard deviation
The sample mean estimates the population mean
So:
\(\bar x =\mu\)
\(\bar x =50\)
The sample standard deviation is calculated as thus:
\(\sigma_x = \frac{\sigma}{\sqrt n}\)
\(\sigma_x = \frac{20}{\sqrt{500}}\)
\(\sigma_x = \frac{20}{22.36}\)
\(\sigma_x = 0.8944\)
Solving (c): The shape of the distribution.
We have:
\(n = 500\) --- The sample size
According to Central limit theorem, When the sample size is greater than 30, then the shape of the distribution is normal.
Hence, the shape is normal
Solving (d): \(P(\bar x \ge 55)\)
Calculate the test statistic (t)
\(t = \frac{\bar x - \mu}{\sigma}\)
\(t = \frac{55 - 50}{0.8945}\)
\(t = \frac{5}{0.8945}\)
\(t = 5.590\)
So:
\(P(\bar x > 55) = P(t > 5.590)\)
Referencing the z table, we have:
\(P(t > 5.590) = 0\)
Hence:
\(P(\bar x > 55) = 0\)
Salut, am si eu o intrebare, care ma cam "bate" pot spune, deoarece imi da rezultate multiple, iar intrebarea este urmatoarea:
Cati bani poti face timp de 6 luni punand cate 5lei/zi? Dar timp de 7luni, a cate 5lei/zi??
Va rog, ajutati-ma cat puteti de repede.
Seara faina!
Dau coroana, daca pot!
Answers
Answer:
sorry
Step-by-step explanation:
Todd rolled a 12-sided die marked with the numbers 1 to 12. These are his experimental probabilities.
P(odd number) = 18/48
P(greater than 8) = 16/48
P(9) = 12/48
1. Which experimental probability matches the theoretical probability exactly?
2. Which experimental probability is farthest from the theoretical probability?
Answers
The experimental probability farthest from the theoretical probability is P(greater than 8). The theoretical probability of rolling a 9 is 1/12 because there is one 9 out of twelve total possible outcomes.
Experimental probability refers to the probability of an event based on data acquired from repeated trials or experiments.
Theoretical probability is the probability of an event occurring based on logical reasoning or prior knowledge. In Todd’s case, he rolled a 12-sided die marked with the numbers 1 to 12.
The probabilities are as follows:P(odd number) = 18/48P(greater than 8) = 16/48P(9) = 12/48To answer the questions:1. Which experimental probability matches the theoretical probability exactly?The theoretical probability of rolling an odd number is 6/12 or 1/2 because there are six odd numbers out of the twelve total possible outcomes.
The experimental probability Todd obtained was 18/48. Simplifying 18/48 to lowest terms gives 3/8, which is equal to 1/2, the theoretical probability.
Therefore, the experimental probability that matches the theoretical probability exactly is P(odd number).2. Which experimental probability is farthest from the theoretical probability? The theoretical probability of rolling a number greater than 8 is 3/12 or 1/4 because there are three numbers greater than 8 out of twelve total possible outcomes.
The experimental probability Todd obtained was 16/48. Simplifying 16/48 to lowest terms gives 1/3, which is not equal to 1/4, the theoretical probability.
The experimental probability Todd obtained was 12/48. Simplifying 12/48 to lowest terms gives 1/4, which is not equal to 1/12, the theoretical probability.
However, the difference between the experimental probability and the theoretical probability for P(9) is smaller than that of P(greater than 8). Therefore, P(greater than 8) is the experimental probability that is farthest from the theoretical probability.
For more such questions on possible outcomes
https://brainly.com/question/30241901
#SPJ8
PLZ HELP WILL GIVE BRAINLIEST!
What ratio do the squares have to the circles? Remember, it's SQUARES TO CIRCLES

Answers
Answer:
A
Step-by-step explanation:
Answer:
this is Easy, the answer is A.
Step-by-step explanation:
just count the number of squares which is 3, and then count the number of circles which is 6.
The store offers a 35% discount. If the regular price of an item is x dollars, what is the discount price in dollars?
Answers
Answer: .35x
Step-by-step explanation:
take the 35% and turn it into a decimal (.35)
Since the item is "X" dollars, multiply the x(.35)
This gives you .35x
Answer:
If there is a 35% discount, first convert the percent to a decimal
35% = 0.35
Then multiply the discount rate by the price of the item
x = item price
0.20x = discounted price
Select the correct answer. Which expression is equivalent to the given expression? (6n^-5)(3n^-3)^2
Answers
The equivalenet expression is 54\(n^{-11}\)
What is expression?Any mathematical statement that includes numbers, variables, and an arithmetic operation between them is known as an expression or algebraic expression.
What is exponent?The way of representing huge numbers in terms of powers is known as an exponent. Exponent, then, is the number of times a number has been multiplied by itself.
To simplify the given expression, we need to apply the power of a power rule, which states that to raise a power to another power, we need to multiply the exponents.
Starting with:
(\(6n^-5\))(\(3n^-3\))²
We can simplify as follows:
(\(6n^-5\))(\(9n^-6\))
Now, we can use the product of powers rule, which states that when multiplying two powers with the same base, we add their exponents.
Therefore:
6 x 9 = 54
\(n^-5 * n^-6 = n^-11\)
So the simplified expression is:
\(54n^-11\)
Therefore, the expression \((6n^-5)(3n^-3)^2\) is equivalent to \(54n^-11.\)
To know more about exponent visit:
https://brainly.com/question/5497425
#SPJ1
The expression that is equal to (6n-5)(3n-3) option D, 54n11.
What is expression?Mathematical expressions consist of at least two numbers or variables, at least one arithmetic operation, and a statement.
We can use the distributive property of multiplication to expand the expression (6n - 5)(3n - 3) as follows:
(6n - 5)(3n - 3) = 6n(3n) - 6n(3) - 5(3n) + 5(3)
= 18n² - 18n - 15n + 15
= 18n² - 33n + 15
Therefore, the expression that is equivalent to (6n - 5)(3n - 3) is 18n² - 33n + 15, which is option D.
So, the answer is option D, 54n11.
To know more about expression visit:
https://brainly.com/question/18189573
#SPJ1
help me pwease? very last minute

Answers
Let \(S_k\) be the k-th partial sum of the infinite series,
\(\displaystyle S_k = \sum_{n=1}^k \frac23 \left(\frac14\right)^{n-1} = \frac23 \left(1 + \frac14 + \frac1{4^2} + \cdots + \frac1{4^{k-1}}\right)\)
Multiply both sides by 1/4 :
\(\displaystyle \frac14 S_k = \frac23 \left(\frac14 + \frac1{4^2} + \frac1{4^3} + \cdots + \frac1{4^k}\right)\)
Subtract this from \(S_k\) and solve for \(S_k\) :
\(\displaystyle S_k - \frac14 S_k = \frac23 \left(1 - \frac1{4^k}\right)\)
\(\displaystyle \frac34 S_k = \frac23 \left(1 - \frac1{4^k}\right)\)
\(\displaystyle S_k = \frac89 \left(1 - \frac1{4^k}\right)\)
Then as k goes to infinity, the exponential term will converge to zero, and the sum will converge to
\(\displaystyle S = \lim_{k\to\infty} S_k = \boxed{\frac89}\)
Generalizing this result, we have for |r| < 1,
\(\displaystyle \sum_{n=1}^\infty a r^{n-1} = \frac a{1-r}\)
A house was valued at $299,000 . Over several years, the value decreased by, 9% giving the house a new value.
(a) Fill in the blank to write the new value in terms of the old value.
Write your answer as a decimal.
(b) Use your answer in part (a) to determine the new value.
Answers
A) - The NEW VALUE in terms of the old value is 0.91 times the old value.
B) - The NEW VALUE of the HOUSE is: 299,000 * 0.91 = $272,090
Step-by-step explanation:Make A Plan:
A) - Calculate the Percentage of the Value Remaining After the Decrease
B) - Calculate the NEW VALUE of the house
SOLVE THE PROBLEM:
A) - The PERCENTAGE of the VALUE REMAINING AFTER the DECREASE
100% - 9% = 91%
As A DECIMAL:0.91
B) - Calculate the NEW VALUE of the house:
NEW VALUE = OLD VALUE * REMAINING PERCENTAGE
NEW VALUE = 299,000 * 0.91
Draw the conclusion:
A) - The NEW VALUE in terms of the old value is 0.91 times the old value.
B) - The NEW VALUE of the HOUSE is: 299,000 * 0.91 = $272,090
I hope it helps!
what is 3 3/4 - 1 1/4?
Answers
Answer:
2 2/4 or 2 1/2
Step-by-step explanation:
3-1=2
3/4-1/4=2/4
2/4=1/2
find the value 3sin²60 + cot²30
Answers
Answer:
21/4
Step-by-step explanation:
3sin²60 + cot²30
sin 60 = √3/2
cot 30 = √3
Substituting values in equation,
3(√3/2)² + (√3)²
=> 3(3/4) + 3
=> 9/4 + 3
=> 9/4 + 12/4
=> 21/4
I’ll give brainliest! Please help

Answers
Answer:
65
Step-by-step explanation:
The lines are parallell so m1 = m5, and m3=m8. 180-115 is 65
A group of students in a communications course are required to start a blog on a topic of their choice, and many have already begun blogging.
pop culture 5
literature 1
business 84
What is the experimental probability that the next blog started will be about pop culture?
Write your answer as a fraction or whole number.
Answers
The probability that the next blog started will be about pop culture is approximately 0.0556. Experimental probability is the probability that is obtained by conducting experiments. Experimental probability is based on how many times an event occurs compared to the number of trials or experiments conducted.
The group of students in a communications course is required to start a blog on a topic of their choice, and many have already begun blogging.
The number of blogs is given below:Pop culture = 5Literature = 1Business = 84The total number of blogs started by the students is 90.The experimental probability that the next blog started will be about pop culture can be calculated by the following formula:Experimental probability = Number of times the event occurs / Total number of trials or experimentsLet E be the event that the next blog started will be about pop culture.
Then the number of times the event occurs is 5.So the experimental probability that the next blog started will be about pop culture is given by:Experimental probability = 5/90 = 1/18The experimental probability that the next blog started will be about pop culture is 1/18 or 0.0556 (rounded to four decimal places).
Therefore, the probability that the next blog started will be about pop culture is approximately 0.0556.
For more such questions on Experimental probability
https://brainly.com/question/8652467
#SPJ8
Which term can be added to the list so that the greatest common factor of the three terms is 12h3?
36h3, 12h6, __________
Answers
The term that can be added to the list so that the greatest common factor of the three terms 12h3 36h3, 12h6, is 48h5
How can the term be known?A group of numbers' greatest common factor (GCF) is the biggest factor that all the numbers have in common. For instance, 12, 20, and 24 all share two characteristics.
The term that can fit in to the list so the GCF is 12h3 would be 48h5, this is so because 48 is first divisible by 12 without any fraction, and we can remove upon dividing 3 h's from this term as it contains a total of 5 h's.
Learn more about greatest common factor at;
https://brainly.com/question/219464
#SPJ1
What is the product?
(3a²b7)(5a³b³)
O 8a5b15
O 8a6b56
O 15a³b¹5
O 15a5b56
Answers
Answer:
15a^5 b^10
Step-by-step explanation:
The product is 15a⁵b¹⁰.
What is an exponent?Exponentiation is one of the mathematics operations.
Let mᵃ, where m and a are the real numbers.
And m is multiplied by a times to itself.
So, a is the exponent of m.
When multiplying two terms with the same base, you add the exponents. Therefore:
(3a²b⁷)(5a³b³) = 3 x 5 x a⁵ x b ¹⁰
= 15a⁵b¹⁰.
To learn more about the exponents;
brainly.com/question/30066987
#SPJ7
Find m and c for this line
Y+3x=1
Answers
Answer:
m = -3 ; c = 1
Step-by-step explanation:
y = -3x + 1
y = mx + c
m = -3
c = 1
2 1/2 : 3 1/2 = n:2what do the : between numbers mean?
Answers
The symbol : denotes that the two ratios are in proportion
\(\begin{gathered} 2\frac{1}{2}\colon3\frac{1}{2}=n\colon2 \\ we\text{ can rewrite it as } \\ \frac{2\frac{1}{2}}{3\frac{1}{2}}=\frac{n}{2\text{ }} \\ In\text{ this form we can easily se}e\text{ that in order to solve for n , we just have to multiply both sides of the equation by 2} \\ 2\cdot\mleft\lbrace\frac{2\frac{1}{2}}{3\frac{1}{2}}=\frac{n}{2\text{ }}\mright\rbrace\cdot2 \\ =\frac{2\cdot2\frac{1}{2}}{3\frac{1}{2}}=n \\ n=\frac{2\cdot2\frac{1}{2}}{3\frac{1}{2}}=\frac{5}{3\frac{1}{2}}=\frac{5}{\frac{7}{2}}=5\cdot\frac{2}{7}=\frac{10}{7} \\ \\ \end{gathered}\)\(2\frac{1}{2}\colon3\frac{1}{2}=n\colon2\)we can rewrite the expression as :
\(\frac{2\frac{1}{2}}{3\frac{1}{2}}=\frac{n}{2\text{ }}\)Now we can see easily that that in order to solve for n , we just have to multiply both sides of the equation by 2
\(2\cdot\lbrace\frac{2\frac{1}{2}}{3\frac{1}{2}}=\frac{n}{2\text{ }}\rbrace\cdot2\)\(=\frac{2\cdot2\frac{1}{2}}{3\frac{1}{2}}=n\)\(n=\frac{2\cdot2\frac{1}{2}}{3\frac{1}{2}}=\frac{5}{3\frac{1}{2}}=\frac{5}{\frac{7}{2}}=5\cdot\frac{2}{7}=\frac{10}{7}\)2) The mean mathematics SAT score in 2012 was 514 with a standard deviation of 117 ("Total group profile," 2012). Assume the mathematics SAT score is normally distributed. a. State the random variable. b. Find the probability that a person has a mathematics SAT score over 700. c. Find the probability that a person has a mathematics SAT score of less than 400. d. Find the probability that a person has a mathematics SAT score between a 500 and a 650. e. Find the mathematics SAT score that represents the top 1% of all scores.
Answers
The mathematics SAT score representing the top 1% of all scores is approximately 780.
a. The random variable in this case is the mathematics SAT score.
b. To find the probability that a person has a mathematics SAT score over 700, we need to calculate the z-score first.
The z-score is calculated as \(\frac{(X - \mu )}{\sigma}\),
where X is the value we're interested in, μ is the mean, and σ is the standard deviation.
In this case, X = 700, μ = 514, σ = 117.
Using the formula, the z-score is \(\frac{(700 - 514)}{117 } = 1.59\).
To find the probability associated with this z-score, we can consult a standard normal distribution table or use a calculator.
The probability is approximately 0.0564 or 5.64%.
c. To find the probability that a person has a mathematics SAT score of less than 400, we again calculate the z-score using the same formula.
X = 400, μ = 514, and σ = 117.
The z-score is \(\frac{(400 - 514) }{117 } = -0.9744\).
Looking up the probability associated with this z-score, we find approximately 0.1635 or 16.35%.
d. To find the probability that a person has a mathematics SAT score between 500 and 650, we need to calculate the z-scores for both values.
Using the formula, the z-score for 500 is \(\frac{(500 - 514)}{117 } = -0.1197\),
and the z-score for 650 is \(\frac{(650 - 514)}{117 } = 1.1624\).
We can then find the area under the normal curve between these two z-scores using a standard normal distribution table or calculator.
Let's assume the probability is approximately 0.3967 or 39.67%.
e. To find the mathematics SAT score that represents the top 1% of all scores, we need to find the z-score corresponding to the top 1% of the standard normal distribution.
This z-score is approximately 2.33.
We can then use the z-score formula to calculate the corresponding SAT score.
Rearranging the formula,
\(X = (z \times \sigma ) + \mu\),
where X is the SAT score, z is the z-score, μ is the mean, and σ is the standard deviation.
Substituting the values,
\(X = (2.33 \times 117) + 514 = 779.61\).
Rounded to the nearest whole number, the mathematics SAT score representing the top 1% of all scores is approximately 780.
For such more questions on mathematics
https://brainly.com/question/29892643
#SPJ8
-13.95 = -0.3m - 2.8m
Answers
Answer: combine like terms then divide dum dum
Step-by-step explanation:
What is the mean, median and mode for...45,50,55,55,55,60,60,60,65,65,70?
Answers
Answer:
Mean = 58.18
Median = 60
Modes = 55 and 60
Step-by-step explanation:
To find the mean/average, add up all the numbers and divide the sum by the # of numbers there are (ex. there are 11 numbers so divide the sum by 11).
The median is the middle number of a set. In this case, the middle number is easy to see because the # of numbers is odd, but if it was even, just find the average of the two middle numbers.
The mode is/are the most frequent number(s) in the set. In this set, the numbers that appear the most are 55 and 60.