if angle B and angle q are acute angles such that sinB=sinQ then prove that angle B = angle Q
Answers
If sin B = sinQ then angle B = angle Q
What is trigonometric ratio?Trigonometric Ratios are defined as the values of all the trigonometric functions based on the value of the ratio of sides in a right-angled triangle.
Trigonometric ratio is applied to right triangles. If one side is already 90°, them the two angles will be an acute angle. An acute angle is am angle that is not upto 90°.
Therefore for Sin B to be equal to SinQ then it shows the two acute angles in the right triangles are thesame.
Therefore ;
90+ x +x = 180
90 + 2x = 180
2x = 180 -90
2x = 90
x = 90/2
x = 45°
This means that B and Q are both 45°
learn more about trigonometric ratio from
https://brainly.com/question/24349828
#SPJ1
Related Questions
Define Each Term.
Slope:
Unite Rate:
Answers
Slope: A number that describes both the direction and steepness of a line
Unit rate:A ratio that is used to compare quantities
Round 0.21 to the nearest whole number.
Answers
Answer:
0
Step-by-step explanation:
.21 is closer to 0 than to 1
After rounding to the nearest whole number, we get;
⇒ 0
We have to given that;
A number is,
⇒ 0.21
And, Round 0.21 to the nearest whole number.
Since, We know that;
Whole numbers are defined from 0 to infinity.
Here, Number is, 0.21
Which is written as,
⇒ 0 < 0.21 < 1
Hence, 0.21 is closer to 0.
So, After rounding to the nearest whole number, we get;
⇒ 0
Learn more about the rounding number visit:
brainly.com/question/27207159
#SPJ6
Giovanna owns a farm. She is going to randomly select one animal to present at the state fair. She has 6 pigs, 4 chickens, and 10 cows. What is the probability that the animal selected is not a chicken ?
Answers
the probability that the animal selected is not a chicken is 4/5 or 0.8, which is the answer.
There are a total of 6 + 4 + 10 = 20 animals on Giovanna's farm.
The probability of selecting a chicken randomly is 4/20 = 1/5, since there are 4 chickens out of 20 animals.
Therefore, the probability of not selecting a chicken is the complement of this probability, which is:
1 - 1/5 = 4/5
what is probability?
Probability is a measure of the likelihood that an event will occur. It is a number between 0 and 1, where 0 represents an impossible event and 1 represents a certain event. The probability of an event is calculated by dividing the number of favorable outcomes by the total number of possible outcomes.
For example, if you flip a fair coin, there are two possible outcomes: heads or tails. The probability of getting heads is 1/2, because there is one favorable outcome (heads) out of two possible outcomes (heads or tails).
To know more about probability visit:
brainly.com/question/21586810
#SPJ11
Oil spilled from a ruptured tanker spreads in a circle whose area increases at a constant rate of 8.5 mi^2/hr. How rapidly is radius of the spill increasing when the area is 7 mi^2?
Answers
To find the rate at which the radius of the oil spill is increasing when the area is 7 mi^2, dr/dt ≈ 0.203 mi/hr the area of the spill is 7 mi^2, dr/dt ≈ 0.203 mi/hr the radius is increasing at a rate of 0.203 mi/hr.
Where A is area and r is the radius. Taking the derivative of both sides with respect to time, we can express the rate of change of the area as dA/dt = 2πr(dr/dt). Given that dA/dt is constant at 8.5 mi^2/hr, we can substitute the values to find the rate at which the radius is increasing.
We have the equation dA/dt = 2πr(dr/dt), where dA/dt represents the rate of change of the area, r is the radius, and dr/dt is the rate at which the radius is changing. We are given that dA/dt is constant at 8.5 mi^2/hr. When the area is 7 mi^2, we can substitute these values into the equation: 8.5 = 2π(7)(dr/dt)
Simplifying the equation, we can solve for dr/dt: dr/dt = 8.5 / (2π(7)) Evaluating the expression, we find: dr/dt ≈ 0.203 mi/hr
Therefore, when the area of the spill is 7 mi^2, the radius is increasing at a rate of approximately 0.203 mi/hr.
To learn more about radius click here : brainly.com/question/13449316
#SPJ11
An excited electron falls from n = 4 to n = 2. a. calculate the energy change in joules associated with this transition.
Answers
To calculate the energy change associated with an electron transitioning from the n = 4 energy level to the n = 2 energy level, we can use the equation for the energy of an electron in an atom, which is given by:
E_n = -13.6 eV * (1/n^2)Where E_n is the energy of the electron in the nth energy level, and eV is the unit of energy called the electronvolt.
Substituting the values of n = 4 and n = 2 into this equation gives us:
E_2 = -13.6 eV * (1/2^2) = -13.6 eV * (1/4) = -3.4 eVE_4 = -13.6 eV * (1/4^2) = -13.6 eV * (1/16) = -0.85 eVThe energy change associated with the transition from n = 4 to n = 2 is given by
E_2 - E_4 = (-3.4 eV) - (-0.85 eV) = -2.55 eV.To convert this energy change from electronvolts to joules, we can use the fact that 1 eV is equal to 1.602176634 x 10^-19 joules.
Multiplying -2.55 eV by this conversion factor gives us an energy change of -2.55 eV * 1.602176634 x 10^-19 joules/eV = -4.13 x 10^-18 joules.
Learn more about Energy here:
https://brainly.com/question/13881533
#SPJ4
Answer the two math questions below for 10 points (sorry for the math spam lol)

Answers
the value of x=1/2 or 2.
What is quadratic equation?
it's a second-degree quadratic equation which is an algebraic equation in x. Ax2 + bx + c = 0, where a and b are the coefficients, x is variable, and c is the constant term, is the quadratic equation in its standard form. A non-zero term (a 0) for the coefficient of x2 is a prerequisite for an equation to be a quadratic equation. The x2 term is written first, then the x term, and finally the constant term is written when constructing a quadratic equation in standard form. In most cases, the numerical values of letters a, b, and c are expressed as integral values rather than fractions or decimals.
Solve the following equation using the zero-product property.
(4x+2) (x-2) = 0
here either 4x+2 = 0 or x-2 = 0
So for 4x+2=0
x = 1/2 or
x-2=0
x=2
Hence the value of x=1/2 or 2.
Learn more about quadratic equation, by the following link.
https://brainly.com/question/1214333
#SPJ1
The bureau of labor statistics classifies people who would like to work but have given up looking for a job as:______.
Answers
People who are looking for a job are unemployed that is the term used by the bureau of labor statistics which classified people who would like to work but have given up .
Step to Step explanation:
People who are jobless and looking for a job are considered in the category of unemployed by the bureau of labor statistics.People in the certain age range and are not working and are looking for a job comes in the category of unemployed.labor force is made by combination of employed and unemployed.Therefore, the people who would like to work but given up who are looking for a job are unemployed classified by bureau of labor statistics.
The complete question is:
The bureau of labor statistics classifies people who would like to work but have given up looking for a job as:______.
a. Unemployed
b. A discouraged worker
c. Not in the labor force
d. Employed
Learn more about statistics here
brainly.com/question/29093686
#SPJ4
5=y/3-9. 14=5k-31. t/9-7=-5. v/8-9=13. 25-13f=-14. i need to find what the letter equals
Answers
Answer:
5(3-9) = y
15 - 45 = y
y = -30
14 = 5k - 31
-5k = -31 - 14
-5k = -45
k = 9
t = -5(9 - 7)
t = -45 + 35
t = -10
v = 13(8-9)
v = 104 - 117
v = -13
13f = 53
f = 4
Answer:
\(\huge{\boxed{\text{ See ~ attached ~ picture.}}}\)
Step-by-step explanation:
Rules for solving an equation :
Collect the terms with the variable to left hand side and constant terms to the right hand side by changing their signs ' + ' to ' -' and ' - ' to ' + '.Simplify and get the single term on each side.Divide each side by the coefficient of variable and then get the values of variable.Hope I helped!
Best regards!
~\(\text{ TheAnimeGirl}\)

Find the product shown below in simplest standard form. (x + 5)(x - 5)
help
Answers
Answer:
Step-by-step explanation:
X^2-5^2
X^-25
is the answer

I need help with tangent geometry! Please help me!

Answers
1. A secant is: segment HF
2. The radius = 8 units; 3. Perimeter of the triangle = 37.6.
What is a Secant?In geometry, a secant is a line that intersects a curve or a circle at two distinct points, and it can be extended infinitely in both directions.
What is the Tangent Theorem?In geometry, the Tangent Theorem states that a line tangent to a circle is perpendicular to the radius that intersects the point of tangency.
1. The name of a secant in the circle shown can be segment HF.
2. DE is tangent to the circle, and DC is the radius, therefore triangle CDE is a right tringle. Applying the Pythagorean theorem, we have the equation:
CD² = 17² - 15²
CD² = 64
CD = 8
Therefore, radius = CD = 8
3. Applying the two-tangent theorem, we have:
Perimeter = 8 + 6.2 + 12.6 + (12.6 - 8) + 6.2
Perimeter = 37.6
Learn more about secant and tangent on:
https://brainly.com/question/26826991
#SPJ1
Solve each system of equations using a matrix.
3x - y = 7 2x + 2y = 10
Answers
The solution is x = 3 and y = 2.
To solve the system of equations using a matrix, we can write the system in matrix form as follows:
[ 3 -1 ] [ x ] [ 7 ]
[ 2 2 ] [ y ] = [ 10 ]
Let's represent the coefficient matrix as A, the variable matrix as X, and the constant matrix as B:
A = [ 3 -1 ]
[ 2 2 ]
X = [ x ]
[ y ]
B = [ 7 ]
[ 10 ]
To find the solution, we can use the equation \(X = A^(-1) * B,\) where \(A^(-1)\) is the inverse of matrix A.
First, let's find the inverse of matrix A:
\(A^(-1) = 1 / (ad - bc) * [ d -b ] [ -c a ]\)
Calculating the determinant (ad - bc):
det(A) = (3 * 2) - (-1 * 2) = 8
Therefore, the inverse of matrix A is:
\(A^(-1) = 1 / 8 * [ 2 1 ] [ -2 3 ]\)
Now, we can calculate the solution matrix X:
\(X = A^(-1) * B\)
Substituting the values:
X = 1 / 8 * [ 2 1 ] * [ 7 ]
[ 10 ]
Calculating the matrix multiplication:
X = 1 / 8 * [ (2*7) + (1*10) ]
[ (-2*7) + (3*10) ]
Simplifying:
X = 1 / 8 * [ 24 ]
[ 16 ]
Therefore, the solution to the system of equations is:
x = 24/8 = 3
y = 16/8 = 2
Hence, the solution is x = 3 and y = 2.
Learn more about coefficient matrix from this link:
https://brainly.com/question/29083712
#SPJ11
Ken spent half of his money. The next day he earned $12. He now has $32. Which equation represents the situation?
Answers
Find the approximate Volume of a Sphere with a diameter of 10.
(Please round your answer to the hundreths place.)
Answers
Answer:
4188.79
Step-by-step explanation:
Formula for volume of a sphere: let V be volume and r be diameter:
V=(4/3)pi(r)^3
Pi can be written as 3.141593

What will be the new function rule for g(x) if it is a Vertical Stretch by a factor of 3 of f(x)=x^3+4
Answers
Answer:
\(g(x)=3x^3+12\)
Step-by-step explanation:
To stretch f(x) by 3, you have the new function of the form \(g(x)=3f(x)\). Plugging in for f(x) gives \(g(x)=3(x^3+4)=3x^3+12\)
Help me find x please!!!

Answers
Answer:
Step-by-step explanation:
2) 133 + a = 180 {Linear pair}
a = 180 - 133
a = 47
a +b = 180 {linear pair}
47 + b = 180
b = 180 - 47
b = 133
x = b + 30 {Exterior angle property}
x = 133 +30
x = 163
3) m + 35+ 35 = 180 {Angle sum property of triangle}
m + 70 = 180
m = 180 - 70
m = 110
z = 35 {alternate interior angles are congruent}
x = m + z
x = 110 + 35
x = 145

Which of these would be a helpful first step in solving the equation? Check all that apply.
9x + 5 = 5x + 21
A. subtract 5x
B. divide by 3
C. subtract 16
D. divide by 9
E. subtract 5
Answers
I believe it would be A and E. Good luck!!:)
Can someone please explain how to solve 2.7÷0.8 step by step please
Answers
Answer: 3 and 3/8 or 27/8
Step-by-step explanation:
First step, you will need to move the decimal to the side by 1 place value.
0.8 --> 8. and 2.7--> 27.
Then just do your normal dividing.
27/8 = 3 and 3/8
The answer to 2.7÷0.8 can be either a mixed number or an improper fraction.
You have to move the decimal places to the right as many times as you need in order to make the number a while number you move the decimal place the same times as you did to the number outside the box which makes is 8 divided by 27 8 can’t go into 2 so u add a 0 and 8 can go into 27 3 times. You add a decimal point and subtract 24 from 27 u get 3 then you add a decimal point with a 0 8 can go into 30 3 times so it’s 6 add a decimal point to make it 60. Then 8 can go into 60 7 times subtract 56 from 60 and you get 4 add a decimal point and you get 40 8 can go into 40 5 times and your answer is 3.375
I added picture so u can see how it looks when you do it.

A bag contains 1 yellow ball and 9 red balls. A ball is chosen at random from the bag. what is the probability of drawing a yellow ball.
Answers
Answer:
1/10
Step-by-step explanation:
10 balls in the bag, there is one yellow
Answer:
answer 1/10
Step-by-step explanation:
Who can help me
Find the volume of the composite solid. Round your answer to the nearest hundredth.

Answers
By Cavalieri's Principle, the volume of that slanted cylinder will be the same volume of a non-slanted cylinder with the same altitude.
so we have a cylinder with a radius of 3 and a height of 7 and a cone hitching a ride on it, with a radius of 3 and a height of 3, so let's simply get the volume of each.
\(\textit{volume of a cylinder}\\\\ V=\pi r^2 h~~ \begin{cases} r=radius\\ h=height\\[-0.5em] \hrulefill\\ h=7\\ r=3 \end{cases}\implies V=\pi (3)^2(7) \\\\[-0.35em] ~\dotfill\\\\ \textit{volume of a cone}\\\\ V=\cfrac{\pi r^2 h}{3}~~ \begin{cases} r=radius\\ h=height\\[-0.5em] \hrulefill\\ h=3\\ r=3 \end{cases}\implies V=\cfrac{\pi (3)^2(3)}{3} \\\\[-0.35em] ~\dotfill\\\\ \pi (3)^2(7)~~ + ~~\cfrac{\pi (3)^2(3)}{3}\implies 63\pi +9\pi \implies 72\pi ~~ \approx ~~ \text{\LARGE 226.19}~in^3\)
PLEASE ANSWER QUICK!!!!! 25 POINTS
Find the probability of exactly one successes in five trials of a binomial experiment in which the probability of success is 5%
round to the nearest tenth
Answers
The probability of exactly one successes in five trials is 0.20
Finding the probability of exactly one successes in five trialsFrom the question, we have the following parameters that can be used in our computation:
Binomial experiment Probability of success is 5%Number of trials = 5The probability is calculated as
P(x) = nCx * p^x * (1 - p)^(n -x)
Where
n = 5
p = 5%
x = 1
Substitute the known values in the above equation, so, we have the following representation
P(1) = 5C1 * (5%)^1 * (1 - 5%)^(5 -1)
Evaluate
P(1) = 0.20
HEnce, the probability value is 0.20
Read more about probability at
https://brainly.com/question/24756209
#SPJ1
Estimate the value of √2π / √5 .
Answers
Answer:
1.12099824328 or estimated is 1
Step-by-step explanation:
Give branliest if i was right!
a ticket broker sold 540 tickets for a concert. the number of tickets sold for this concert is 80% of the concert hall's seats. what is the total number of seats in the concert hall? psat
Answers
Answer: 432
Step-by-step explanation:
540 x 0.8
A solid with surface area 50units^2 is dilated by a scale factor of K to obtain a solid surface area 200units^2. Find the value of K.
Answers
The value of K is 2.
Let's denote the scale factor as K. The surface area of a solid after dilation is directly proportional to the square of the scale factor.
We are given that the initial surface area of the solid is 50 units^2, and after dilation, the surface area becomes 200 units^2.
Using the formula for the surface area, we have:
Initial surface area * (scale factor)^2 = Final surface area
50 * K^2 = 200
Dividing both sides of the equation by 50:
K^2 = 200/50
K^2 = 4
Taking the square root of both sides:
K = √4
K = 2
Therefore, the value of K is 2.
for such more question on scale factor
https://brainly.com/question/3381225
#SPJ8
Please help ! The equation is attached in the photo above :)

Answers
Step-by-step explanation:
Hi
HiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHiHi
ANSWER
My answer is in the photo above
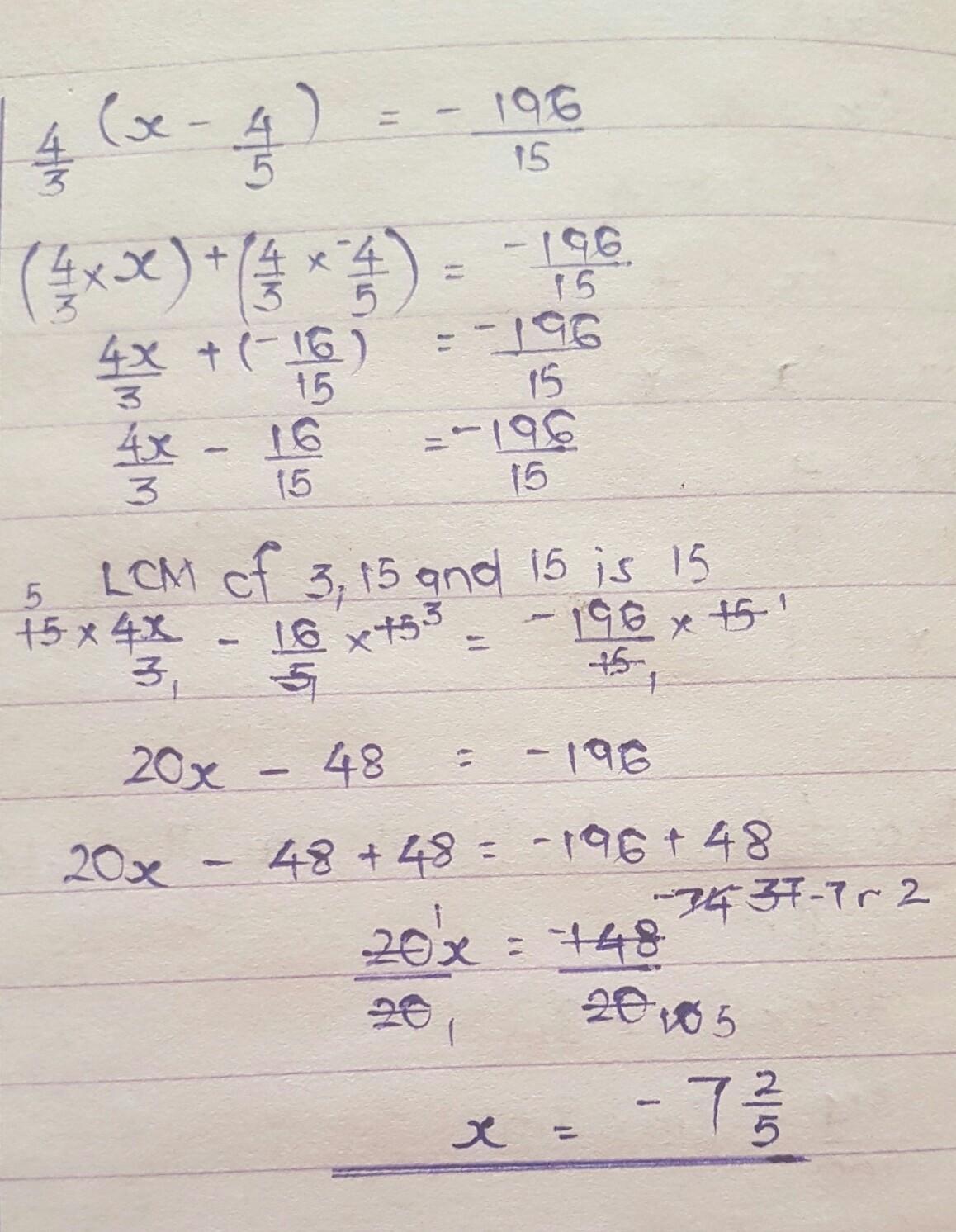
a team has twelve 15-year-old players and eight 16-year-old players. the coach of the team is 43 years old. which measure of central tendency best represents the ages of the team, including the coach, and why?
Answers
The best measure of central tendency to represent the ages of the team, including the coach, would be the mean or average age.
To calculate the mean, we add up all the ages and divide by the total number of people:
Mean = (Sum of all ages) / (Total number of people)
In this case, we have:
12 players who are 15 years old
8 players who are 16 years old
1 coach who is 43 years old
So, the total number of people is 12 + 8 + 1 = 21.
The sum of all the ages is:
12 × 15 (years old) + 8 × 16 (years old) + 43 (years old) = 180 + 128 + 43 = 351 (years old)
Therefore, the mean age of the team is:
Mean = 351 / 21 = 16.71 (rounded to two decimal places)
The mean is a good measure of central tendency because it takes into account all the ages in the team, including the coach, and provides an average value that is representative of the ages of the entire team. It is also a useful measure for making comparisons between different groups or teams based on their age and to estimate the mean ages of various people.
Learn more about mean;
https://brainly.com/question/1136789
#SPJ4
explain what the following correlation coefficient tell you about two sets of data r=0.4
Answers
If r is between 0 and 1 it is a positive correlation
if r is between -1 and 0 it is a negative correlation
\(0In this case, for r=0.4, The correlation is positive. It's a weak associationT/F: Nonsampling errors reduce the overall quality of data regardless of the data collection method.
Answers
True. Nonsampling errors refer to errors that occur during the data collection process that are not related to the sampling method used. These errors can occur in any type of data collection method, whether it be through surveys, experiments, or observational studies.
Nonsampling errors can arise due to a variety of reasons, such as poor survey design, biased sampling methods, inadequate training of surveyors, errors in data entry or processing, or even deliberate fraud.
Nonsampling errors can have a significant impact on the quality of the data collected, as they can introduce biases and inaccuracies into the results. These errors can result in incorrect conclusions and decisions based on the data, which can have serious consequences. Therefore, it is important to take steps to minimize nonsampling errors during the data collection process, such as carefully designing surveys, ensuring proper training of surveyors, and conducting thorough quality checks on the data collected.
Learn more about Nonsampling here:
https://brainly.com/question/15396688
#SPJ11
Activity 3
I bought a bag of 60
lollipops.
I kept 3 and gave
the rest to my 3 friends.
They divided the lollipops
equally among themselves.
How many did each friend
get?
Answers
Answer:
19 Lollipops per friend
Step-by-step explanation:
\(60-3=57\\\\57/3=19\)
Answer:
19
You kept 3 So the rest equal 60 - 3 = 57Then you gave the rest to 3 friends So each one will take 57/3 = 19Please help with this

Answers
1) (a) The transformations that occur from the parent function are horizontal translation of 2 units to the left and vertical translation of 4 units to the down.
(b) (-2, -4)
(c) Graph is given below.
1) Given a function,
g(x) = (x + 2)² - 4
(a) Given a parent function p(x) = x².
We can write g(x) as,
g(x) = p(x + 2) - 4
So the transformation is horizontal translation of 2 units to the left and vertical translation of 4 units to the down.
(b) Vertex formula of a parabola is,
y = a (x - h)² + k, where (h, k) is the vertex.
Comparing the given function with vertex form,
Vertex of the parabola = (-2, -4)
(c) Graph of g(x) will be a parabola with vertex at (-2, -4).
It is given below.
Learn more about Transformations here :
https://brainly.com/question/23186655
#SPJ1
For what values of k will the function f(x) = 9x² + 4x + k have 1 real roots.
Answers
Hello,
Answer:
for k = 4/9
Step-by-step explanation:
a = 9 ; b = 4 ; c = k
we search Δ = 0 (because 1 real root)
Δ = b² - 4ac = 4² - 4 × 9 × k = 16 - 36k
Δ = 0 ⇔ 16 - 36k = 0 ⇔ 36k = 16 ⇔ k = 16/36 = (4 × 4)/(4 × 9) = 4/9
⇒ k = 4/9
Answer:
\(\{\frac{4}{9} \}\)
Step-by-step explanation:
First off, we are given a parabola by definition:
\(f(x) = 9x^2 + 4x + k \\ a = 9, b = 4, c = k;\)
Since \(a > 0\), our parabola has an upward opening.
Should we think about it graphically, it will be no wonder that we should pay our attention to the points of the parabola intersecting the abscissa axis. In other words, we need our vertex to intersect the x axis only once per se.
The vertex:
\(V_{x} = \frac{-b}{2a} = \frac{-4}{2 * 9} = - \frac{2}{9} \\ V_{y} = 9V_{x}^2 + 4V_{x} + k = 9(- \frac{2}{9})^2 + 4(- \frac{2}{9}) + k = 9 * \frac{4}{9^2} - \frac{8}{9} + k = \frac{4}{9} - \frac{8}{9} + k = - \frac{4}{9} + k\)
As a result, our \(V_{y}\) is parametric. \(k = \frac{4}{9}\) suits us because \(V_{y} = - \frac{4}{9} + \frac{4}{9} = 0\). If \(k > \frac{4}{9}\), we do not have any roots at all. We have two roots if \(k < \frac{4}{9}\).
