If the radius of a cone increases at a rate of 36 inches per second and the height decreases 2 feet per second, determine the rate of change of volume when the diameter is 12 feet, and the height is 10 feet
Answers
To determine the rate of change of volume, we can use the formula for the volume of a cone:
V = (1/3)πr²h
Given that the radius is increasing at a rate of 36 inches per second (or 3 feet per second since 1 foot is equal to 12 inches) and the height is decreasing at a rate of 2 feet per second, we need to find the rate of change of volume when the diameter is 12 feet and the height is 10 feet.
First, we need to determine the rate of change of the radius and the height at the specific moment when the diameter is 12 feet and the height is 10 feet.
Since the diameter is 12 feet, the radius is half of that, which is 6 feet. Therefore, the rate of change of the radius is 3 feet per second.
The rate of change of the height is given as -2 feet per second.
Now, we can substitute these values into the volume formula and calculate the rate of change of volume:
V = (1/3)π(6)²(10)
V = 120π cubic feet
To find the rate of change of volume, we can use the product rule for differentiation:
dV/dt = (1/3)π(2r)(dr/dt)(h) + (1/3)π(r²)(dh/dt)
Substituting the given values:
dV/dt = (1/3)π(2)(6)(3)(10) + (1/3)π(6²)(-2)
dV/dt = 120π - 24π
dV/dt = 96π cubic feet per second
Therefore, the rate of change of volume when the diameter is 12 feet and the height is 10 feet is 96π cubic feet per second.
Learn more about volume here: brainly.com/question/32541821
#SPJ11
Related Questions
The range of a linear transformation must be a subset of the domain.a. trueb. false
Answers
False. The range of a linear transformation is a subset of the codomain, not the domain.
The domain is the set of inputs to the transformation, while the codomain is the set of possible outputs. The range is the set of actual outputs produced by the transformation. The statement "The range of a linear transformation must be a subset of the domain" is false. The range of a linear transformation is a subset of the codomain, not the domain. The domain is the set of input vectors, while the codomain contains the possible output vectors after applying the linear transformation.
To know more about linear transformation visit:
https://brainly.com/question/13595405
#SPJ11
Sasha works for the Humane Society and had to buy food for the dogs. She buys 1614 pounds of dog food. She feeds each dog about 58 of a pound. How many dogs can she feed?
26
25
10
6
Answers
27 but 27 isn't there so do 26
Answer: A
Step-by-step explanation: because when dividing 58 into 1614 it equals 27.23 but the answer choice isn't there so i would choose 26
suppose that the 13th term of an arithmetic sequence is 46 and the fourth term is 100. find the expression for the general term.
Answers
To solve this problem, we need to use the formula for the nth term of an arithmetic sequence:
an = a1 + (n-1)d where a1 is the first term, d is the common difference, and n is the term number. This means that the first term is 118, the common difference is -6, and each subsequent term is found by subtracting 6 from the previous term.
We know that the 4th term is 100, so we can substitute this into the formula:
a4 = a1 + (4-1)d
100 = a1 + 3d
Similarly, we know that the 13th term is 46:
a13 = a1 + (13-1)d
46 = a1 + 12d
Now we have two equations with two unknowns (a1 and d), which we can solve by elimination or substitution. I will use elimination:
100 = a1 + 3d
-46 = -a1 - 12d
------
54 = -9d
d = -6
Now we can substitute d back into one of the equations to solve for a1:
100 = a1 + 3(-6)
a1 = 118
Therefore, the expression for the general term of the arithmetic sequence is:
an = 118 - 6(n-1) or an = 124 - 6n
For more questions on arithmetic sequence
https://brainly.com/question/6561461
#SPJ11
The relationship between V, the volume of a cube, and E, the length of each edge of the cube, is shown below.
3/V= E
E
What is the length, in inches, of each edge of a cube that has a volume of 64 cubic inches?
Answers
Answer: 4 inches.
Step-by-step explanation:
Given: The relationship between V, the volume of a cube, and E, the length of each edge of the cube is given by :-
\(\sqrt[3]{V}=E\)
If volume = 64 cubic inches, then put V= 64, we get
\(\sqrt[3]{64}=E\\\\\Rightarrow\ \sqrt[3]{4\times 4\times 4} =E\\\\\Rightarrow\ \sqrt[3]{4^3} =E\\\\\Rightarrow\ 4 =E\)
Hence, the length of each edge of a cube = 4 inches.
Help it’s due by Thursday

Answers
Answer:
10 is B. 9 is 28.8
Step-by-step explanation:
A store sells an 8-pound bag of flour for $18.80. If larry can buy a 2-pound bag of flour at the same rate, what would be the price of the 2-pound bag?
Answers
Answer:
$4.70
Step-by-step explanation:
First, you need to divide 18.80 by 8.
18.80/8 = 2.35
2.35 is the unit price for one (1) pound bag of flour,
Multiply by 2 to find the price of a two (2) pound bag.
2.35 * 2 = 4.7
$4.70 is the price of a two-pound bag.
hope this helps :)
it takes bill 2 hours longer to do a certain job than it takes cindy. they worked together for 2 hours, then cindy left and bill finished the job in 1 hour. how long would it take each of them to do the job alone
Answers
It takes Cindy 1 hour to do the job alone and Bill 3 hours to do the job alone.
Let x be the time it takes Cindy to do the job alone, in hours. Then, it takes Bill x + 2 hours to do the job alone.
During the first 2 hours, when they worked together, they did 2/x + 2/(x + 2) = 1/2 of the job.
Bill finished the job in 1 hour after Cindy left, so he did 1/x + 2 = 1/3 of the job during that hour.
We can now set up a system of two equations to solve for x:
2/x + 2/(x + 2) = 1/2 (1)
1/x + 2 = 1/3 (2)
From equation (1), we can find x + 2:
2/x + 2/(x + 2) = 1/2
2x + 4 = x(x + 2)
2x + 4 = x^2 + 2x
x^2 - 2x + 4 = 0
(x - 4)(x - 1) = 0
x = 4 or x = 1
Since x represents the time it takes Cindy to do the job, we reject x = 4 and keep x = 1.
Substituting x = 1 into equation (2), we find:
1/1 + 2 = 1/3
3 = 3
So, it takes Cindy 1 hour to do the job alone and Bill 3 hours to do the job alone.
Therefore, It takes Cindy 1 hour to do the job alone and Bill 3 hours to do the job alone.
To learn more about Time and work,
Visit; brainly.com/question/8032570
#SPJ4
It takes Cindy 1 hour to do the job alone and Bill 3 hours to do the job alone.
Let x be the time it takes Cindy to do the job alone, in hours. Then, it takes Bill x + 2 hours to do the job alone.
During the first 2 hours, when they worked together, they did 2/x + 2/(x + 2) = 1/2 of the job.
Bill finished the job in 1 hour after Cindy left, so he did 1/x + 2 = 1/3 of the job during that hour.
We can now set up a system of two equations to solve for x:
2/x + 2/(x + 2) = 1/2 (1)
1/x + 2 = 1/3 (2)
From equation (1), we can find x + 2:
2/x + 2/(x + 2) = 1/2
2x + 4 = x(x + 2)
2x + 4 = x² + 2x
x² - 2x + 4 = 0
(x - 4)(x - 1) = 0
x = 4 or x = 1
Since x represents the time it takes Cindy to do the job, we reject x = 4 and keep x = 1.
Substituting x = 1 into equation (2), we find:
1/1 + 2 = 1/3
3 = 3
So, it takes Cindy 1 hour to do the job alone and Bill 3 hours to do the job alone.
Therefore, It takes Cindy 1 hour to do the job alone and Bill 3 hours to do the job alone.
To learn more about Time and work,
brainly.com/question/8032570
#SPJ4
If 5k = -25, then 5k - 1 = -25 - 1
Segment proof
Answers

Find the limit of the following sequence or determine that the sequence diverges. {2n^3-1/3n^3+1}
Select the correct choice below and fill in any answer boxes to complete the choice. A. The limit of the sequence is (Type an exact answer.) B. The sequence diverges.
Answers
The limit of {2n³-1/3n³+1} is 2/3. So option a) is the right answer. The sequence does not diverge.
To determine the limit of the given sequence {2n³-1/3n³+1}, we can use the concept of limit rules. We can simplify the given sequence by dividing both numerator and denominator by n³, which gives:
{2n³-1/3n³+1} = {2-1/n³}/{3+1/n³}
As n approaches infinity, 1/n³ approaches zero, which means that the denominator of the fraction approaches 3. The numerator of the fraction approaches 2. Therefore, we can conclude that the given sequence approaches the limit of 2/3 as n approaches infinity.
Hence, the correct choice is:
A. The limit of the sequence is 2/3.
It is essential to find the limit of the sequence as it helps in determining the behavior of the sequence as it approaches infinity. In mathematics, the concept of the limit of a sequence is widely used in analyzing and solving many problems.
By finding the limit of a sequence, we can understand the behavior of the sequence, and we can use it to make predictions or analyze the given situation. Repetition of a sequence of measurements helps us to obtain an average or expected value, which can be used for further analysis.
Know more about limit here:
https://brainly.com/question/12211820
#SPJ11
Juanita walked 4 miles on a park trail in 1 1/3 hours. What was her average speed in miles per hour?
Answers
8 less than the quotient of a number and 4
Answers
Answer:
(n/4)- 8
Step-by-step explanation:
a number= "n"
(n/4)-8
Use the solution method from this example to find a basis for the given subspace. S = span {[1 -1 0 2], [3 -5 4 8], [0 1 -2 -1]} Give the dimension of the basis. v
Answers
Answer:
Step-by-step explanation:
The dimension of the basis is {[1 0 0 2], [-1 1 0 0]}.
To find a basis for the subspace S = span {[1 -1 0 2], [3 -5 4 8], [0 1 -2 -1]}, we can use the same method as in the example. First, we put the vectors in a matrix and row-reduce it:
[1 -1 0 2]
[3 -5 4 8]
[0 1 -2 -1]
R2 - 3R1 -> R2
R3 -> R3 + 2R1
[1 -1 0 2]
[0 -2 4 2]
[0 1 -2 -1]
-1/2R2 -> R2
[1 -1 0 2]
[0 1 -2 -1]
[0 1 -2 -1]
R3 - R2 -> R3
[1 -1 0 2]
[0 1 -2 -1]
[0 0 0 0]
We can see that the last row is all zeros, so we have only two pivots and one free variable. This means that the dimension of the subspace S is 2. To find a basis, we can write the pivots as linear combinations of the original vectors:
[1 -1 0 2] = [1 0 0 2] + [-1 1 0 0]
[0 1 -2 -1] = [0 1 -2 -1]
Therefore, a basis for S is {[1 0 0 2], [-1 1 0 0]}.
Visit here to learn more about subspace:
brainly.com/question/31691975
#SPJ11
Given a sample mean is 82, the sample size is 100, 90% confidence level and the population standard deviation is 20. Calculate the margin of error to 2 decimals.
Answers
Given a sample mean is 82, the sample size is 100, 90% confidence level and the population standard deviation is 20, the margin of error is 3.29.
To calculate the margin of error, we need to use the formula:
Margin of error = Z-score * (population standard deviation / square root of sample size)
Where the Z-score corresponds to the confidence level. Since we have a 90% confidence level, the Z-score is 1.645.
Plugging in the given values, we get:
Margin of error = 1.645 * (20 / sqrt(100))
Margin of error = 1.645 * 2
Margin of error = 3.29 (rounded to 2 decimals)
Therefore, the margin of error is 3.29.
More on margin of error: https://brainly.com/question/29101642
#SPJ11
Find the slope \mathrm{m}m of the line in the graph below. \mathrm{m} =m=

Answers
Answer:
\(m=4\) or \(m=\frac{4}{1}\)
Step-by-step explanation:
To find slope we use the slope formula
\(m=\frac{y_{2} -y_{1} }{x_{2} -x_{1} }\)
Two points on the line we can classify are (3,4) and (4,8)

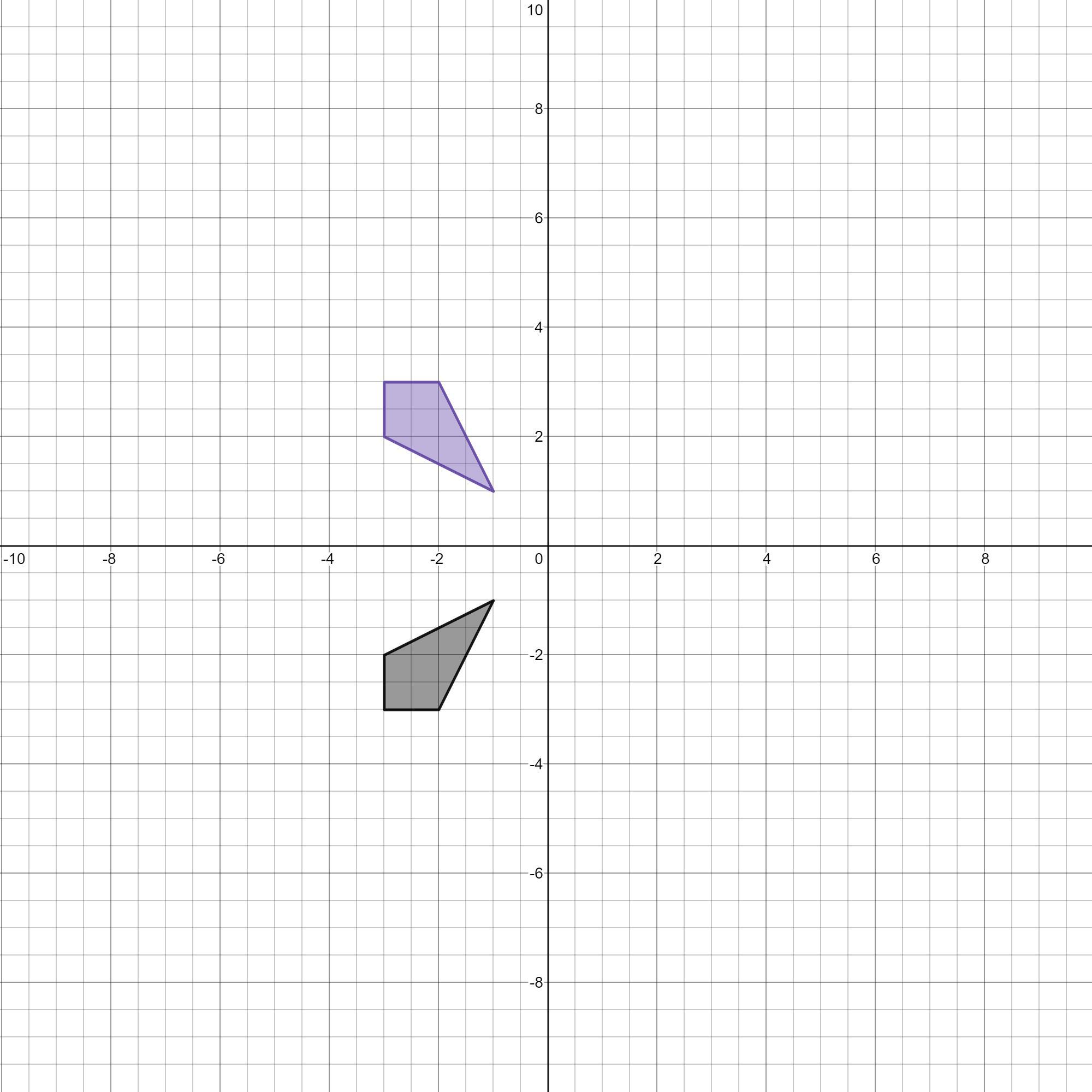
In which quadrant will the image of figure PQRS be located after a reflection across the x-axis?

Answers
To answer this question, we can remember that when we reflect a point (x, y) across the x-axis, the point is (x, -y).
1. From the graph, we have that the coordinates of the figure are in Quadrant II. Since the figure will have the same values for x but will change the values from y to -y, then the figure will be reflected on Quadrant III.
2. For instance, if we have the points of the figure PQRS are:
• P(-3, 3)
,• Q(-2, 3)
,• R(-1, 1)
,• S(-3, 2)
3. After a reflection across the x-axis, and following the rule for this transformation, we will have that the image for that pre-image will be:
• P(-3,3) ---> P'(-3, -(3)) ---> P'(-3, -3)
,• Q(-2, 3) ---> Q'(-2, -3)
,• R(-1, 1) ---> R'(-1, -1)
,• S(-3, 2) ---> S'(-3, -2)
We can see Quadrant III above.
And we can see that all of the values for the coordinates pairs are negative, and this is possible in Quadrant III where the values for x and y are negative.
In summary, therefore, we can conclude that the image of figure PQRS will be located in Quadrant III (third option).

DOES THIS HAVE ONE SOLUTION , NO SOLUTIONS ,OR INFINITELY MANY SOLUTIONS?! 30 points

Answers
Answer:
INFINITELY MANY SOLUTIONS
Step-by-step explanation:
INFINITELY MANY SOLUTIONS
PLEASE HELPP RIGHT NOW

Answers
Answer: May
Step-by-step explanation:
two forces with magnitudes of 300 pounds and 500 pounds act on an object at angles of 60° and - 45° respectively, with the positive x-axis. find the magnitude and direction of the resultant force
Answers
The magnitude of the resultant force can be found using the law of cosines, and it is approximately 692 pounds.
The direction of the resultant force can be found using the law of sines, and it is approximately 14.6° with respect to the positive x-axis
To find the magnitude of the resultant force, we can use the law of cosines. The law of cosines states that in a triangle, the square of one side is equal to the sum of the squares of the other two sides minus twice the product of their magnitudes and the cosine of the included angle.
In this case, the two sides are the magnitudes of the given forces (300 pounds and 500 pounds), and the included angle is the angle between the forces.
Applying the law of cosines, we have: Resultant force^2 = 300^2 + 500^2 - 2 * 300 * 500 * cos(60° - (-45°))
Calculating this equation, we find that the resultant force^2 is approximately equal to 479,200 pounds^2. Taking the square root of this value, we get the magnitude of the resultant force, which is approximately 692 pounds.
To find the direction of the resultant force, we can use the law of sines. The law of sines states that in a triangle, the ratio of the length of a side to the sine of its opposite angle is constant.
In this case, the sides are the magnitudes of the forces, and the opposite angles are the angles between the forces and the positive x-axis.
Applying the law of sines, we have: (sin θ) / 500 = (sin 60°) / Resultant force
Solving for θ, we find that sin θ is equal to (sin 60°) / (Resultant force / 500). Calculating this equation, we get sin θ is approximately 0.250.
Taking the inverse sine of this value, we find that θ is approximately 14.6°. Therefore, the direction of the resultant force is approximately 14.6° with respect to the positive x-axis.
To know more about angle click here
brainly.com/question/14569348
#SPJ11
A triangle has side lengths of (2b+5c)(2b+5c) centimeters, (10b+7d)(10b+7d) centimeters, and (4d-3c)(4d−3c) centimeters. Which expression represents the perimeter, in centimeters, of the triangle?
Answers
We can conclude that the expression that represents the perimeter, in centimeters, of our triangle is:
P = (12b + 2c + 17d) cm
Which expression represents the perimeter of the triangle in centimeters?We know that the sides of our triangle measure:
side 1: (2b + 5c)cmside 2: (10b + 7d) cmside 3: (4d - 3c) cmAnd we want to get the perimeter of our triangle, which is basically the sum of the lengths of the 3 sides, so the equation for the perimeter is:
P = (2b + 5c)cm + (10b + 7d) cm + (4d - 3c) cm
Now we need to simplify that expression, we will get:
P = (2b + 5c + 10b + 7d + 4d - 3c) cm
P = (2b + 10b + 5c - 3c + 7d + 10d) cm
P = (12b + 2c + 17d) cm
Then we can conclude that the expression that represents the perimeter, in centimeters, of our triangle is:
P = (12b + 2c + 17d) cm
If you want to learn more about the perimeter:
https://brainly.com/question/397857
#SPJ1
Given the following returns, what is the variance? Year 1 = 16%;
year 2 = 6%; year 3 = -25%; year 4 = -3%.
.0344
.0209
.0306
.0297
.0268
Answers
The variance for the given data set: Year 1 = 16%; Year 2 = 6%; Year 3 = -25%; Year 4 = -3% is 0.0344.
The variance given the following returns:
Year 1 = 16%, Year 2 = 6%, Year 3 = -25%, Year 4 = -3% is 0.0344.
In probability theory, the variance is a statistical parameter that measures how much a collection of values fluctuates around the mean.
Variance, like other statistical measures, is used to describe data.
A variance is a square of the standard deviation, which is a numerical term that determines the amount of dispersion for a collection of values.
Variance provides a numerical estimate of how diverse the values are.
If the data points are tightly clustered, the variance is small.
If the data points are spread out, the variance is large.For a given data set, we may use the following formula to compute variance:
\($$\sigma^2 = \frac{\sum_{i=1}^{N}(x_i-\mu)^2}{N-1}$$\)
Where \($$\sigma^2$$\) is variance, \($$\sum_{i=1}^{N}$$\) is the sum of the data set, \($$x_i$$\) is each data point, \($$\mu$$\) is the sample mean, and \($$N-1$$\) is the sample size minus one.
In the above question, we will calculate the variance for the given data set:
Year 1 = 16%; Year 2 = 6%; Year 3 = -25%; Year 4 = -3%.
\($$\mu=\frac{(16+6+(-25)+(-3))}{4}=-1.5$$\)
Using the formula mentioned above,
\($$\sigma^2 = \frac{\sum_{i=1}^{N}(x_i-\mu)^2}{N-1}$$$$\)
=\(\frac{[(16-(-1.5))^2 + (6-(-1.5))^2 + (-25-(-1.5))^2 + (-3-(-1.5))^2]}{4-1}$$\)
After solving this expression,
\($$\sigma^2=0.0344$$\)
For more related questions on variance:
https://brainly.com/question/14116780
#SPJ8
Consider the following function f(x)=x4+3, x>=0.Find an explicit formula for f^-1
Answers
The explicit formula for f^-1 is (x-3)^(1/4) and this is obtained by switching the roles of x and y and solving for y in terms of x.
To find the inverse function of f(x)=x^4+3, we need to switch the roles of x and y, and solve for y.
Let y = x^4+3
Subtract 3 from both sides to get:
y - 3 = x^4
Take the fourth root of both sides to isolate x:
(x^4)^(1/4) = (y-3)^(1/4)
Simplify:
x = (y-3)^(1/4)
So the inverse function of f(x) is:
f^-1 (x) = (x-3)^(1/4)
This is the explicit formula for the inverse function of f(x).
To know more about explicit formula visit:
https://brainly.com/question/18069156
#SPJ11
6. Which is longer, a mile or a kilometer? How can you tell?
ANSWER ASAP GIVING BRAINLIEST
Answers
Answer:
A mile is longer
Step-by-step explanation:
Solve the equation. (Enter your answers as a comma-separated list.) (x-9)(x+5)=0 x=
Answers
We can write these solutions of equation as a comma-separated list: 9, -5.
To solve the equation (x - 9)(x + 5) = 0, we can use the zero product property, which states that if the product of two factors is equal to zero, then at least one of the factors must be zero.
Therefore, we can set each factor equal to zero and solve for x.
This gives us two possible solutions:x - 9 = 0 or x + 5 = 0
Solving for x in the first equation, we get:x = 9
Solving for x in the second equation, we get:
x = -5
Therefore, the solutions to the equation (x - 9)(x + 5) = 0 are x = 9 and x = -5.
We can write these solutions as a comma-separated list: 9, -5. equation using the zero-product principle.
Learn more about equation at
https://brainly.com/question/29114259
#SPJ11
Does the set of numbers represent a right triangle?
20, 25, 15
Answers
Answer:
No.
Step-by-step explanation:
20+25+15 = 60
A right is 90°. Therefore, 20, 25, and 15 do not make a right angle.
A change in a pyramid has a height of 6 inches of area of the base 11 in.² what is the volume of the pyramid cubic inches?
Answers
Answer:
Volume = 22 in³
Step-by-step explanation:
volume of a pyramid is given by the equation:
volume = base area × (height ÷ 3)
\(V = A_b \times \frac{h}{3} \\\)
\(where:\\V = Volume = ?\\A_b = Base\ area = 11\ in^2\\h = height = 6\ in\\\therefore V = 11 \times \frac{6}{3}\\V = 11 \times 2 = 22\\Volume = 22\ in^3\)
If the expression 4x 3 is equal to 1 for some value of x, what is the expression 4x 8 equal to for the same value of x?
Answers
This expression yields: 4x^8 = 4 * (1/4)^(8/3)
If the expression 4x^3 is equal to 1 for some value of x, we can find the value of x by solving the equation:
4x^3 = 1
Dividing both sides of the equation by 4, we get:
x^3 = 1/4
Taking the cube root of both sides, we find:
x = (1/4)^(1/3)
Now, to determine the value of the expression 4x^8 for the same value of x, we substitute the value of x into the expression:
4x^8 = 4 * ((1/4)^(1/3))^8
Simplifying this expression yields:
4x^8 = 4 * (1/4)^(8/3)
Further simplification depends on whether you want an exact answer or an approximation. If you need an approximate value, please provide the desired level of precision.
Learn more about expression from
brainly.com/question/1859113
#SPJ11
given that the absolute value of the difference of the two roots of $ax^2 + 5x - 3 = 0$ is $\frac{\sqrt{61}}{3}$, and $a$ is positive, what is the value of $a$?
Answers
The value of "a" is approximately 1.83 given that the absolute value of the difference of the two roots of the quadratic equation "ax squared plus 5x minus 3 equals 0" is the square root of 61 divided by 3, and "a" is positive.
We are given that the absolute value of the difference between the two roots of the quadratic equation "ax squared plus 5x minus 3 equals 0" is the square root of 61 divided by 3, and "a" is positive. We need to find the value of "a".
Let the two roots of the equation be r1 and r2, where r1 is not equal to r2. Then, we have:
|r1 - r2| = √(61) / 3
The sum of the roots of the quadratic equation is given by r1 + r2 = -5 / a, and the product of the roots is given by r1 × r2 = -3 / a.
We can express the difference between the roots in terms of the sum and product of the roots as follows:
r1 - r2 = √((r1 + r2)² - 4r1r2)
Substituting the expressions we obtained earlier, we have:
r1 - r2 = √(((-5 / a)²) + (4 × (3 / a)))
Simplifying, we get:
r1 - r2 = √((25 / a²) + (12 / a))
Taking the absolute value of both sides, we get:
|r1 - r2| = √((25 / a²) + (12 / a))
Comparing this with the given expression |r1 - r2| = √(61) / 3, we get:
√((25 / a²) + (12 / a)) = √(61) / 3
Squaring both sides and simplifying, we get:
25 / a² + 12 / a - 61 / 9 = 0
Multiplying both sides by 9a², we get:
225 + 108a - 61a² = 0
Solving this quadratic equation for "a", we get:
a = (108 + √(108² + 4 × 61 × 225)) / (2 × 61)
Since "a" must be positive, we take the positive root:
a = (108 + √(108² + 4 × 61 × 225)) / (2 × 61) ≈ 1.83
Therefore, the value of "a" is approximately 1.83.
Learn more about absolute value at
https://brainly.com/question/1301718
#SPJ4
The question is -
Given that the absolute value of the difference of the two roots of the quadratic equation "ax squared plus 5x minus 3 equals 0" is the square root of 61 divided by 3, and "a" is positive, what is the value of "a"?
a grocer stacks oranges in a pyramid-like stack whose rectangular base is 5 oranges by 8 oranges. each orange above the first level rests in a pocket formed by four oranges below. the stack is completed by a single row of oranges. how many oranges are in the stack?
Answers
The total number of oranges in the pyramidal stack is 78.
The oranges are stacked by the grocer in a pyramid like shape,
The base of the pyramid is rectangular with a size of 5 by 8 oranges,
So, total number of oranges in the base can be found as,
= 5 x 8
= 40 oranges.
One orange has four oranges below it. So, if there are 40 oranges in the base, the upper layer will have one row of oranges reduced from each side of the rectangular base.
So, every next level will have (L-1)(B-1) oranges, where L and B are the length and breadth of every preceding rectangle.
Hence, Oranges in level 1 = 4x8
Oranges in level 2 = 3x7
Oranges in level 3 = 2x6
Oranges in level 4 = 1x5
Hence, total oranges are, (40+21+12+5) oranges.
Total oranges stacked are 78 oranges.
To know more about pyramidal shape, visit,
https://brainly.com/question/1869460
#SPJ4
A store manager kept track of the number of newspapers sold each week over a seven-week period. The results are shown below. \( 87,87,215,154,288,235,231 \) Find the median number of newspapers sold.
Answers
The median number of newspapers sold over seven weeks is 223.
The median is the middle score for a data set arranged in order of magnitude. The median is less affected by outliers and skewed data.
The formula for the median is as follows:
Find the median number of newspapers sold. (87, 87, 215, 154, 288, 235, 231)
We'll first arrange the data in ascending order.87, 87, 154, 215, 231, 235, 288
The median is the middle term or the average of the middle two terms. The middle two terms are 215 and 231.
Median = (215 + 231)/2
= 446/2
= 223
In statistics, the median measures the central tendency of a set of data. The median of a set of data is the middle score of that set. The value separates the upper 50% from the lower 50%.
Hence, the median number of newspapers sold over seven weeks is 223.
To know more about the median, visit:
brainly.com/question/300591
#SPJ11
Solve for m. m + 95 /
4 = 5
Answers
Answer:
m = -75/4
Step-by-step explanation:
1. Subtract 95/4 from both sides
m + 95/4 = 5
x + 95/4 - 95/4 = 5 - 95/4
2. Simplify, which will get you -75/4