if the standard error of the estimate of β1 is 1.22, then the true value of β1 lies between and . as the number of observations in a data set grows, you would expect this range to _____ Increase/ Decrease_____ in size.
Answers
As the number of observations in a data set grows, you would expect this range to decrease in size because the width of the confidence interval will decrease, resulting in a narrower range of possible values for the true value of β1.
To determine the range of the true value of β1, we need to use a confidence interval. Assuming a 95% confidence level, the range of the true value of β1 would be:
β1 ± t(0.025, df) x SE(β1)
where t(0.025, df) is the t-value for a 95% confidence level with (n-2) degrees of freedom, and SE(β1) is the standard error of the estimate of β1.
Since we don't know the degrees of freedom or the value of β1, we cannot calculate the exact range of the true value. However, we can say that the range will be centered around the estimated value of β1 with a width determined by the product of the t-value and the standard error.
As the number of observations in a data set grows, the standard error of the estimate of β1 will generally decrease, since there is more data to estimate the true value of β1. This means that the width of the confidence interval will also decrease, resulting in a narrower range of possible values for the true value of β1.
Therefore, as the number of observations grows, we would expect the range to decrease in size.
To know more about confidence interval refer here:
https://brainly.com/question/24131141#
#SPJ11
Related Questions
a bag contains 6 nickels, 5 dimes, and 4 quarters. if you draw 3 coins at random from the bag, without replacement, what is the probability that you will get a nickel, a quarter, and a nickel, in that order?
Answers
Answer:
nickel=2/5, quarter=4/15, dime=1/3
Step-by-step explanation:
Total number of coins in the bag = 6 + 5 + 4 = 15
Probability of getting a nickel =
\( \frac{6}{15} \)
which is also equivalent to
\( \frac{2}{5} \)
Probability of getting a quarter=
\( \frac{4}{15} \)
Probability of getting a dime=
\( \frac{5}{15} \)
which is equivalent to
\( \frac{1}{3} \)
in a normal distirubtion what percentage of the scores in the distribtion falls one standard devation on either sideo fhte mean
Answers
Answer: In any normal distribution with mean μ and standard deviation σ : Approximately 68% of the data fall within one standard deviation of the mean. Approximately 95% of the data fall within two standard deviations of the mean. Approximately 99.7% of the data fall within three standard deviations of the mean.
Step-by-step explanation:
- 2 = 2+v/4 solve for the variable
Answers
Hey there! :)
Answer:
v = -16.
Step-by-step explanation:
Given:
-2 = 2 + v/4
Subtract 2 from both sides:
-2 -2 = 2 - 2 + v/4
-4 = v/4
Multiply both sides by 4:
-4 · 4 = v/4 · 4
-16 = v
Which scatter plot could have
A trend line with the equation below?
Y=x+4

Answers
Answer:
you're correct the second one
Step-by-step explanation:
without using symmetry, determine a definite integral that represents the area of the region enclosed by r = 1 sin θ .
Answers
The definite integral that represents the area of the region enclosed by the polar curve r = 1 sin θ is ∫[a, b] 1/2 r^2 dθ
To determine the definite integral that represents the area of the region, we integrate the expression 1/2 r^2 with respect to θ over the interval [a, b], where a and b are the limits of the region.
In this case, the polar curve r = 1 sin θ represents a circle with radius 1 centered at the origin. As θ varies from 0 to π, the curve traces half of the circle in the positive direction. To find the area of the region enclosed by this curve, we integrate the expression 1/2 r^2 over this interval.
The expression 1/2 r^2 represents the area of a sector of the circle with radius r and central angle θ. Integrating this expression with respect to θ gives us the total area enclosed by the curve.
By evaluating the definite integral over the interval [a, b], we can find the area of the region enclosed by the polar curve r = 1 sin θ.
To know more about area click here
brainly.com/question/13194650
#SPJ11
[Question 1] You are working with a population of crickets. Before the mating season you check to make sure that the population is in Hardy-Weinberg equilibrium, and you find that the population is in equilibrium. During the mating season you observe that individuals in the population will only mate with others of the same genotype (for example Dd individuals will only mate with Dd individuals). There are only two alleles at this locus ( D is dominant, d is recessive), and you have determined the frequency of the D allele =0.6 in this population. Selection acts against homozygous dominant individuals and their survivorship per generation is 80%. After one generation the frequency of DD individuals will decrease in the population. F
Answers
:According to the question:You are working with a population of crickets. Before the mating season you check to make sure that the population is in Hardy-Weinberg equilibrium, and you find that the population is in equilibrium.
During the mating season you observe that individuals in the population will only mate with others of the same genotype (for example Dd individuals will only mate with Dd individuals). There are only two alleles at this locus ( D is dominant, d is recessive), and you have determined the frequency of the D allele =0.6 in this population. Selection acts against homozygous dominant individuals and their survivorship per generation is 80%. After one generation the frequency of DD individuals will decrease in the population.
According to the Hardy-Weinberg equilibrium equation p² + 2pq + q² = 1, the frequency of D (p) and d (q) alleles are:p + q = 1Thus, the frequency of q is 0.4. Here are the calculations for the Hardy-Weinberg equilibrium:p² + 2pq + q² = 1(0.6)² + 2(0.6)(0.4) + (0.4)² = 1After simplifying, it becomes:0.36 + 0.48 + 0.16 = 1This means that the population is in Hardy-Weinberg equilibrium. This is confirmed as the frequencies of DD, Dd, and dd genotypes
To know more about equilibrium visit:
https://brainly.com/question/12427197
#SPJ11
A ladder leans against the wall of a building. The ladder measures
41 inches and forms an angle of 42° with the ground. How far from
the ground, in inches, is the top of the ladder? How far from the
wall, in inches, is the base of the ladder? Round to two decimal
places as needed.
Answers
We can use trigonometry to solve this problem. Let's call the height of the ladder "h" and the distance from the wall to the base of the ladder "d".
From the problem, we know that the ladder forms a 42° angle with the ground. This means that the sine of the angle is equal to the opposite side (h) over the hypotenuse (41 inches):
sin(42°) = h/41
We can solve for h by multiplying both sides by 41 and taking the sine of 42°:
h = 41 × sin(42°)
h ≈ 28.61 inches
So the top of the ladder is about 28.61 inches from the ground.
To find the distance from the wall to the base of the ladder, we can use the cosine of the angle:
cos(42°) = d/41
We can solve for d by multiplying both sides by 41 and taking the cosine of 42°:
d = 41 × cos(42°)
d ≈ 31.15 inches
So the base of the ladder is about 31.15 inches from the wall.
8. higher order thinking use the number line to compare skip
counting by 4s four times to skip counting by 8s two times. how are
skip counting by 4s and 8s alike? how are they different? explain.
0 1
2 3
4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Answers
They differ in step size, the number of terms, and the starting point. Skip counting by 4s has a smaller step size and more terms compared to skip counting by 8s.
When skip counting by 4s four times, we start at 4 and then add 4 repeatedly: 4, 8, 12, 16.
When skip counting by 8s two times, we start at 8 and then add 8 repeatedly: 8, 16.
Both skip-counting sequences have the number 8 in common, which represents a common multiple of 4 and 8.
However, there are differences between skip counting by 4s and skip counting by 8s.
1. Step size: When skip counting by 4s, the step size is 4. We add 4 to the previous number each time. On the other hand, when skip counting by 8s, the step size is 8. We add 8 to the previous number each time.
2. Number of terms: In skip counting by 4s, we have four terms (4, 8, 12, 16). In skip counting by 8s, we have two terms (8, 16).
3. Starting point: Skip counting by 4s starts at 4, while skip counting by 8s starts at 8.
In summary, skip counting by 4s and 8s are alike in that they both involve adding multiples of a number. They differ in step size, the number of terms, and the starting point. Skip counting by 4s has a smaller step size and more terms compared to skip counting by 8s.
To learn more about Skip counting visit:
brainly.com/question/31852464
#SPJ11
Solve:4 to the 6th power times 4 to the fourth power
Answers
Answer:
4¹⁰
Step-by-step explanation:
You don do the figuring out want number is in each exponent you simply add because you have the same base and if its multiplication you actually do addition in which multiplication is repeated addition. same for division but subtraction instead because you are lowing the number :)
4 to the 4th power= 256
4,096+256= 1048576
Find the value of z that corresponds to the following: a) Area = 0.1210 b) Area = 0.9898 c) 45th percentile
Answers
a) The value of z corresponding to an area of 0.1210 can be found using statistical tables or a statistical calculator.
b) Similarly, the value of z corresponding to an area of 0.9898 can be obtained using statistical tables or a statistical calculator.
c) To find the value of z at the 45th percentile, we can use the standard normal distribution table or a statistical calculator.
a) To find the value of z corresponding to an area of 0.1210, you can use a standard normal distribution table or a statistical calculator. By looking up the area of 0.1210 in the table, you can determine the corresponding z-value. For example, if you find that the z-value for an area of 0.1210 is -1.15, then -1.15 is the value of z corresponding to the given area.
b) Similarly, to find the value of z corresponding to an area of 0.9898, you can refer to a standard normal distribution table or use a statistical calculator. Find the z-value that corresponds to the area of 0.9898. For instance, if the z-value for an area of 0.9898 is 2.32, then 2.32 is the value of z corresponding to the given area.
c) To find the value of z at the 45th percentile, you can use a standard normal distribution table or a statistical calculator. The 45th percentile corresponds to an area of 0.4500. By finding the z-value for an area of 0.4500, you can determine the value of z at the 45th percentile. For example, if the z-value for an area of 0.4500 is 0.125, then 0.125 is the value of z at the 45th percentile.
To learn more about area Click Here: brainly.com/question/22469440
#SPJ11
James buys a shirt and a pair of socks on sale for 25% off. If the price of the shirt before the sale was $24 and he spent a total of $24, what was the original price of the socks? Enter your answer in the box.
Answers
Answer:
The price of the socks is dollar 8
Pls mark nrainliest
Answer:
$8
Step-by-step explanation:
Using the information we already know, we can form an equation:
Let x be the socks' original price.
\((24+x)\) × \(0.75=24\)
Divide both sides by 0.75
\(24+x=32\)
Subtract 24 from both sides
\(x=8\)
The socks' original price was $8.
) Given the integral ∫
0
1
∫
y
1
∫
0
z
f(x,y,z)dxdzdy Given five other equivalent iterated integrals. That is, give the iterated integrals in the orders dydzdx,dxdydz,dydxdz,dzdxdy, and dzdydx.
Answers
\(The given integral is ∫[0,1]∫[y,1]∫[0,z]f(x,y,z)dxdzdy.\) We need to find five equivalent iterated integrals in different order
\(The first iterated integral in dydzdx order is∫[0,1]∫[0,z]∫[y,1]f(x,y,z)dydxdz.\)
\(The second iterated integral in dxdydz order is∫[0,1]∫[0,1]∫[0,z]f(x,y,z)dxdydz.\)
\(The third iterated integral in dydxdz order is∫[0,1]∫[0,1]∫[0,z]f(x,y,z)dydxdz.\)
\(The fourth iterated integral in dzdxdy order is∫[0,1]∫[0,1]∫[y,1]f(x,y,z)dzdxdy.\)
\(The fifth iterated integral in dzdydx order is∫[0,1]∫[0,1]∫[y,1]f(x,y,z)dzdydx.\)
Therefore, the five equivalent iterated integrals are∫[0,1]∫[0,z]∫[y,1]f(x,y,z)dydxdz, ∫[0,1]∫[0,1]∫[0,z]f(x,y,z)dxdydz, ∫[0,1]∫[0,1]∫[0,z]f(x,y,z)dydxdz, ∫[0,1]∫[0,1]∫[y,1]f(x,y,z) daddy\(∫[0,1]∫[0,z]∫[y,1]f(x,y,z)dydxdz, ∫[0,1]∫[0,1]∫[0,z]f(x,y,z)dxdydz,\), and \(∫[0,1]∫[0,1]∫[y,1]f(x,y,z)dzdy\)dx.
To know more about the word integral visits :
https://brainly.com/question/31059545
#SPJ11
I WILL MARK BRAINLIEST.
Find the product of 3.2 x 1012 and 4.25 x 109. Write the final answer in scientific notation.
1.36 x 1021
13.6 x 1021
1.36 x 1022
13.6 x 1022
Answers
The product in scientific notation is 1.36 x 10^22
How to find the product of 3.2 x 1012 and 4.25 x 109?The product expression is given as:
3.2 x 1012 and 4.25 x 109
Express the product, properly
3.2 x 10^12 x 4.25 x 10^9
Regroup the factors
3.2 x 4.25 x 10^12 x 10^9
Evaluate the product
13.6 x 10^21
Rewrite as:
1.36 x 10^22
Hence, the product in scientific notation is 1.36 x 10^22
Read more about scientific notation at
https://brainly.com/question/5756316
#SPJ1
Answer:
c 1.36 x 1012
explanation:
If x+1=7, what is the value of x2 + 22 +1?
Answers
Answer:
59
Step-by-step explanation:
x+1 = 7
Subtract 1 from each side
x+1-1 =7-1
x =6
x^2 + 22 +1
6^2 +22+1
36+22+1
36+23
59
Answer:
\(x + 1 = 7 \\ x = 7 - 1 = 6 \\ putting \: the \: value \: of \: x = 6 \\ 6 \times 2 + 22 + 1 = 34\)
For this graph, mark the statements that are true.
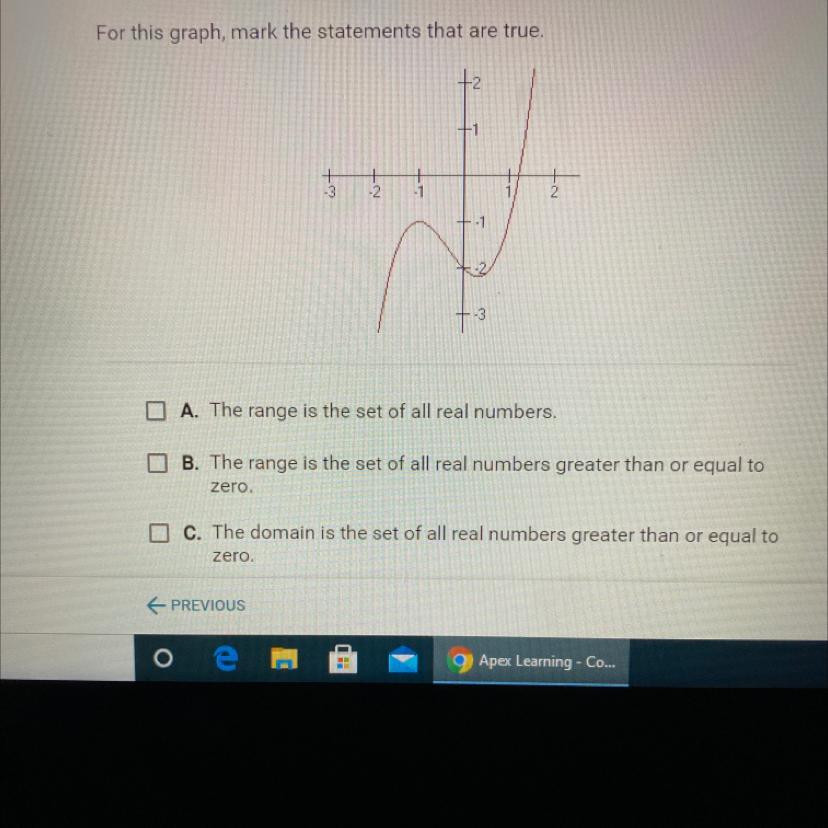
Answers
Answer:
B
Step-by-step explanation:
Just answer it
BBSJSSJJSNSNNSOAOOALAKA
Answer:
A. The domain is the set of all real numbers.
D. The range is the set of all real numbers.
Step-by-step explanation:
The graph shows a polynomial function.
These are defined for any real values of x.
A deli has two platters of sandwiches. The first platter costs $54 and you get 2 roast beef sandwiches and 5 ham sandwiches. The other platter costs $59 and you get 5 roast beef sandwiches and 3 ham sandwiches. Let x represent the cost of each roast beef sandwich and y represent the cost of each ham sandwich. What is the system of linear equations for the given scenario? What is the cost of each sandwich? I just need to know how much each sandwich costs
Answers
Answer:
Cost of each roast beef sandwich = $7
Cost of each ham sandwich = $8
Step-by-step explanation:
x = cost of each roast beef sandwich
y = cost of each ham sandwich
2x + 5y = 54 (1)
5x + 3y = 59 (2)
Multiply (1) by 5 and (2) by 2
10x + 25y = 270
10x + 6y = 118
Subtract to eliminate x
25y - 6y = 270 - 118
19y = 152
Divide both sides by 19
y = 152 / 19
= 8
y = $8
Substitute y = 8 into (1)
2x + 5y = 54 (1)
2x + 5(8) = 54
2x + 40 = 54
2x = 54 - 40
2x = 14
x = 14 / 2
x = $7
Cost of each roast beef sandwich = $7
Cost of each ham sandwich = $8
Investment increase exponentially by about 26% every 3 years. if you start with $2,000 investment how much money would you have after 45 years
Answers
Using an exponential function, it is found that you would have an amount of $64,060 in 45 years.
What is an exponential function?An increasing exponential function is modeled by:
\(A(t) = A(0)(1 + r)^t\)
In which:
A(0) is the initial value.r is the growth rate, as a decimal.In this problem, considering the initial value of A(0) = 2000, with a growth rate of r = 0.26 each 3 years, the equation is given by:
\(A(t) = 2000(1.26)^{\frac{t}{3}}\)
In 45 years, the amount will be given by:
\(A(45) = 2000(1.26)^{\frac{45}{3}} = 64060\)
More can be learned about exponential functions at https://brainly.com/question/25537936
#SPJ1
Students in 7th grade took a standardized math test that they also took in 5th grade. The results are shown on the dot plot, with the most recent data shown first.
Find and compare the medians.
7th-grade median:
5th-grade median:
What is the relationship between the medians?
Answers
Using the median concept, it is found that:
The 5th-grade median is of 13.The 7th-grade median is of 17.The relationship is that 7th grade students have a higher median than 5th grade students.What is the median of a data-set?The median of the data-set separates the bottom half from the upper half, that is, it is the 50th percentile.
Researching the problem on the internet, we have that there are 21 5th grade students. It is an odd number, hence the median is the 11th element, as (21 + 1)/2 = 11. Looking at the dot plot, the median is of 13.
There are 23 5th grade students. It is an odd number, hence the median is the 12th element, as (23 + 1)/2 = 12. Looking at the dot plot, the median is of 17.
The relationship is that 7th grade students have a higher median than 5th grade students.
More can be learned about the median of a data-set at https://brainly.com/question/17110151
#SPJ1
Which of the following rational functions is graphed below?

Answers
The correct option is C, The given graph represents the rational function \(\frac{1}{(x-1)(x-2)}\).
Explain graph.Mathematicians use graphs to variable logically depict or chart sentences or values in a visual way. Usually, a graph point shows the connection between two or more objects. A graph is a particular kind of non-linear side chain up of parts known as nodes as well as lines. The borders, also referred to as nodes, should be joined together with glue. The node numbers in this graph are 1, 2, 3, and 5.
Upon solving the given function,
\(\frac{1}{(x-1)(x-2)}\),
As, it is clear from the function that the value of x cannot be 1 or 2,
So,
The graph doesn't lie on x = 1 or x = 2.
So, it is the correct option.
To know more about graphs visit:
brainly.com/question/11950136
#SPJ1
Which ordered pair is a solution to the system of linear equations?
2x + 3y= 6
–3x + 5y = 10
(0,2)
(2,0)
(3,2)
(2,3)
Answers
The solution of the system of linear equations 2x + 3y = 6 and -3x + 5y = 10 is (0, 2).
Linear equation:
Linear equation refers an equation in which the highest power of the variable is always 1. It is also called as a one-degree equation.
Given,
Here we have the following system of linear equations.
2x + 3y = 6
-3x + 5y = 10
Now, we need to find the solution for the equations.
Here we have to use the substitution method to solve this one,
To do the substitution method we have to follow the following steps:
Step 1) Solve anyone of the equations either for the variable x or y
Step 2) Now, substitute the value obtained from step 1 to the other equation
Step 3) Finally, solve the equation to find the value of the remaining variable.
Here we have to take the equation (2), and we have to solve it for the value of y,
For that we have to rewrite the equation as,
5y = 10 + 3x
y = (10 + 3x)/5
Apply the value of y on the equation (1), in order to get the value of x,
So,
2x + 3(10 +3x)/5 = 6
2x + (30 + 9x)/5 = 6
(10x + 9x + 30)/5 = 6
19x + 30 = 30
19x = 0
x = 0
Now, apply the value of x on the equation in order to get the value of y,
y = (10 + 3(0))/5
y = 10/5
y = 2.
Therefore, the resulting ordered pairs for the system of linear equation is (0, 2).
To know more about Linear equation here.
https://brainly.com/question/11897796
#SPJ1
a swimming pool in the shape of a rectangular prism has dimensions of 16 feet by 12.5 feet by 5 feet. what is the maximum amount of water that the pool can hold?
Answers
The maximum amount of water that the pool can hold is 1000 cubic feet.
To find the maximum amount of water that the rectangular prism swimming pool can hold, we need to calculate its volume.
The volume of a rectangular prism is given by:
V = l x w x h
where l is the length, w is the width, and h is the height of the prism.
Given the dimensions of the swimming pool, we have:
l = 16 feet
w = 12.5 feet
h = 5 feet
Therefore, the volume of the swimming pool is:
V = l x w x h
V = 16 feet x 12.5 feet x 5 feet
V = 1000 cubic feet
To know more about Rectangular Prism:
https://brainly.com/question/21308574
#SPJ4
Riddle!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Who is that with a neck and no head, two arms and no hands? What is it?
Answers
its a shirt................
Answer:
a Shirt
Step-by-step explanation:
of course
Fifty people enter a contest in which three identical prizes will be awarded. In how many different ways can the prizes be awarded to the entrants
Answers
There are 117600 ways for the distribution of the prizes.
According to the statement
We have given that the number of people enter in a contest is 50.
And
Number of prizes given identically is 3.
And we have to find that the by how many ways can be prizes be awarded.
So,
Provided that no one can receive more than one prize,
It means The first prize can be given to any of the 50 people, the second to any of the remaining 49, and the third to the remaining of the 48,
Here we use Permutation
Then the possibilities become is
50*49*48= 117600
So there are above written ways to distribute the prizes.
There are 117600 ways for the distribution of the prizes.
Learn more about Permutation here https://brainly.com/question/4658834
#SPJ4
Why did the National Assembly break away from the Estates General?
Answers
After Louis XVI's failed attempts to sabotage the Assembly and to keep the three estates separate, the Estates-General ceased to exist, becoming the National Assembly. It renamed itself the National Constituent Assembly on July 9 and began to function as a governing body and constitution-drafter.
National assembly
The National Assembly was the first revolutionary government of the French Revolution and existed from June 14th to July 9th in 1789. The National Assembly was created amidst the turmoil of the Estates-General that Louis XVI called in 1789 to deal with the looming economic crisis in France.
Learn more about National assembly here : -
https://brainly.com/question/9891529
#SPJ4
E and F are sets of real numbers defined as follows.
E={v I v≤v3}
F={v I v>6}
Write E∪F and E∩F using interval notation.
If the set is empty, write ∅.
Answers
The union of the sets is E ∪ F = (-∞, 3] or (6, ∞) and the intersection of the sets E ∩ F = ∅ (null sets) is in interval notation.
What is set?
A set is a collection of clearly - defined unique items. The term "well-defined" applies to a property that makes it simple to establish whether an entity actually belongs to a set. The term 'unique' denotes that all the objects in a set must be different.
We have:
E and F are sets of real numbers defined as follows. E={v | v ≤ 3} F={v | v > 6}
E ∪ F = (-∞, 3] or (6, ∞)
E ∩ F = ∅ (null sets)
Thus, the union of the sets is E ∪ F = (-∞, 3] or (6, ∞) and the intersection of the sets E ∩ F = ∅ (null sets) is in interval notation.
Learn more about the set here:
https://brainly.com/question/8053622
#SPJ1
Raíz cuadrada de 157
Answers
Answer:12.5
Step-by-step explanation:
Volume? serious answers please.

Answers
here you goooo <3
find the indefinite integral by using the substitution x = 5 sec(). (use c for the constant of integration.) x2 − 25 x dx
Answers
The given expression is x² - 25x.
To solve for the indefinite integral using the substitution x = 5 sec(), we will use the following steps:
Find the value of dx in terms of dθ.
Substitute x = 5 sec() in the given expression.
Use the identity 1 - sec²(θ) = tan²(θ) to simplify the expression.
Evaluate the indefinite integral.
Therefore, Find the value of dx in terms of dθ.
dx/dθ = 5 sec(θ) tan(θ)dθ
Substitute x = 5 sec(θ) in the given expression.
x² - 25x = (5 sec(θ))² - 25(5 sec(θ))= 25 [sec²(θ) - 5sec(θ)]
Use the identity 1 - sec²(θ) = tan²(θ) to simplify the expression.
= 25 [1 - (1/cos²(θ))] - 125/cos(θ)= 25 [tan²(θ)] - 125/cos(θ)
.Evaluate the indefinite integral by substituting u = tan(θ) and du = sec²(θ) dθ.
∫[25 tan²(θ) - 125/cos(θ)] dθ
= ∫[25 u² du - 125/(1 - u²)] (1/u²) du
= ∫ [25 - 125/(u²(1 - u²))] du
= 25u + (125/2) ln |(u - 1)/(u + 1)| + c
Substitute u = tan(θ)
= 25 tan²(θ) + (125/2) ln |(tan(θ) - 1)/(tan(θ) + 1)| + c.
Therefore, the indefinite integral is given by 25x²/25 + (125/2) ln |(x/5 - 1)/(x/5 + 1)| + c.
#SPJ11
Learn more about substitution and indefinite integral https://brainly.com/question/26568631
How do I solve number 4 and 5 to get the correct answer?

Answers
Answer:
4. (d)
5. (b)
Step-by-step explanation:
You want to apply the secant and chord rules to the circles given in the diagram.
The secant rule is "the product of distances from the point of intersection of secants to the two points of intersection of the secant with the circle is the same for both secants." A tangent can be considered to be a secant that has both points of intersection with the circle in the same place.
The chord rule is similar to the secant rule: "The product of distances from the point of intersection of the chords to their intersection with the circle is the same for both chords."
4.The diagram shows a tangent of length 12, so the product of distances to the two points of intersection with the circle is 12(12).
The secant has length 8 to the near point of intersection, and (x+8) to the far point of intersection. That product is the same as for the tangent:
8(x +8) = 12(12) . . . . . . matches choice D
5.One chord has lengths of 14 and x, so the product of those is 14x.
The other chord has lengths of 12 and 21, so the product of those is 12(21).
The product is the same for both chords, meaning ...
14x = 12(21) . . . . . . matches choice B
__
Additional comment
We have purposely tried to write the rules in "parallel" fashion, because we find them easier to remember that way. Considering a tangent to be a secant with the points of intersection with the circle merged means the same rule can be used for all three cases:
intersecting secants, a tangent intersecting a secant, and intersecting chords.Find the solution of the Neumann problem for the LaPlace equation
\bigtriangledown ^2U(x,y)=0; U_{x}(0,y)=cos(4 \pi x)=U_x(4,y)=U_y(x,0)=U_y(x,4)
On the square region
R={(x,y):x\varepsilon [0,4], y\varepsilon [0,4]}
Answers
The required solution is,
\(\[U(x, y) = -4sin(4\pi x)sinh(\frac{\pi}{4}y) - \sum_{n=2}^{\infty} \frac{64}{n^2\pi^2}sin(\frac{n\pi}{4})cos(\frac{n\pi}{4}x)sinh(\frac{n\pi}{4}y)\]\)
Neumann problem for the LaPlace equation
The given LaPlace equation is as follows:
\(\[\bigtriangledown ^2U(x,y)=0\]\)
And the given values are,\
\([U_{x}(0,y)=cos(4 \pi x)=U_x(4,y)=U_y(x,0)=U_y(x,4)\]\)
On the square region
\[R={(x,y):x\varepsilon [0,4], y\varepsilon [0,4]}\]
To find the solution of the Neumann problem for the LaPlace equation, we need to integrate U(x, y) with respect to x and y.
Integrating the function w.r.t x, we get,
\(\[\int^4_0 \int^4_0 \frac{\partial^2 U}{\partial x^2}dx dy=0\]\)
Integrating the function w.r.t y, we get,
\(\[\int^4_0 \int^4_0 \frac{\partial^2 U}{\partial y^2}dx dy=0\]\)
Now, integrating the function w.r.t x, and applying the given boundary conditions, we get,
\(\[\int^4_0 U_x(0,y)dy= -\int^4_0 U_x(4,y)dy\]\[\int^4_0 cos(4\pi x)dy = - \int^4_0 U_x(4,y)dy\]\[sin(4\pi x) \Big|_0^4 = -\int^4_0 U_x(4,y)dy\]\[0 - 0 = -\int^4_0 U_x(4,y)dy\]Therefore,\[\int^4_0 U_x(4,y)dy = 0\]\)
Now, integrating the function w.r.t y, and applying the given boundary conditions, we get,
\(\[\int^4_0 U_y(x,0)dx = \int^4_0 U_y(x,4)dx\]\)
Therefore,
\(\[U_y(x, 0) = U_y(x, 4) = 0\]\)
Now, using the Fourier series, the solution of the given LaPlace equation is,
\(\[U(x, y) = \sum_{n=0}^{\infty} a_n cos(\frac{n\pi}{4}x)sinh(\frac{n\pi}{4}y)\]\)
Now, applying the given boundary conditions,
\(\[U_x(0, y) = \sum_{n=0}^{\infty} \frac{na_n\pi}{4} sin(\frac{n\pi}{4}x)cosh(\frac{n\pi}{4}y) = cos(4\pi x)\]\[U_x(4, y) = \sum_{n=0}^{\infty} \frac{na_n\pi}{4} sin(\frac{n\pi}{4}x)cosh(\frac{n\pi}{4}y)\]\[U_y(x, 0) = \sum_{n=0}^{\infty} a_n cos(\frac{n\pi}{4}x)sinh(0)\]\[U_y(x, 4) = \sum_{n=0}^{\infty} a_n cos(\frac{n\pi}{4}x)sinh(n\pi)\]\)
Now, solving the above equations, we get,
\(\[a_1 = -4sin(4\pi x)\]And\[a_n = - \frac{64}{n^2\pi^2}sin(\frac{n\pi}{4})\]\)
Therefore, the required solution is,
\(\[U(x, y) = -4sin(4\pi x)sinh(\frac{\pi}{4}y) - \sum_{n=2}^{\infty} \frac{64}{n^2\pi^2}sin(\frac{n\pi}{4})cos(\frac{n\pi}{4}x)sinh(\frac{n\pi}{4}y)\]\)
To know more about solution visit:
https://brainly.com/question/30109489
#SPJ11