In order for Brady to earn a B in his biology course, his test scores must average at least 80%. On the first 5 tests, he
has an average of 77%. There is one test remaining in the course. Write an inequality then find what is the
minimum score Brady needs to earn on the last test to receive a B in the class?
Answers
Answer:
x ≥83%
Step-by-step explanation:
77%+x/2=80% (×b.s by 2)
77%+x=160%
x=160%-77%
x=83%
Related Questions
The table shows the number of absences in a school year and the final exam scores for several students. An equation of the line of fit through (3, 85) and (4, 81) is y=−4 x+97 . Interpret the slope and the y-intercept.

Answers
For the equation slope and y-intercept are respectively, -4 and 97
What is the equation of line?A straight line's equation is a relationship between its x and y coordinates, and it is written as y = mx + c, where m is the line's slope and c is its y-intercept.
The rate of change of y with respect to x is shown by the slope of a line in the equation y = mx + b.
The value of y when x is 0 is represented by the y-intercept of a line in the equation y = mx + b. The y-intercept in this situation is 97, which indicates that a student's expected final exam score is 97 if they have no absences.
Therefore, the following interpretation can be made for the line of fit's slope and y-intercept:
The final exam score drops by 4 points for every additional absence, according to the slope of -4.
The y-intercept of 97 implies that a student's final exam grade would be 97 if they had no absences.
To know more about Line check:
https://brainly.com/question/17188072
#SPJ
The function f(x)=1/6(2/5)^x is reflected across the y-axis to create the function g(x). Which ordered pair is on g(x)?
Answers
Answer:
the ordered pair (0, 1/6)
Step-by-step explanation:
To reflect a function across the y-axis, we replace every occurrence of x with -x. Therefore, the function g(x) is given by:
g(x) = f(-x) = 1/6(2/5)^(-x)
To find an ordered pair on g(x), we need to choose a value of x and evaluate g(x). For example, if we choose x = 0, then:
g(0) = 1/6(2/5)^(-0) = 1/6
Therefore, the ordered pair (0, 1/6) is on the graph of g(x).
Let X be a continuous random variable with the following density function: 1 f(x) = 3*, 0
Answers
Let X be a continuous random variable with the following density function: 1 f(x) = 3*, 0 < x < 1. Compute the expected value and variance of X.
Expected value: The expected value or the mean of the continuous random variable X is given by μ= ∫x * f(x) dx, where f(x) is the probability density function of the continuous random variable X, and the integral is taken over the entire range of X. In this case, f(x) = 3, 0 < x < 1. Therefore, the expected value or the mean of X is given by:
μ= ∫x * f(x) dx = ∫x * 3 dx (0 < x < 1).
On integrating, we get: μ= [3/2 * x²]₀¹= 3/2 * 1² - 3/2 * 0²= 3/2. The expected value of X is 3/2 or 1.5. Variance: The variance of the continuous random variable X is given byσ²= ∫(x - μ)² * f(x) dx, where f(x) is the probability density function of the continuous random variable X, and the integral is taken over the entire range of X. In this case, f(x) = 3, 0 < x < 1, and μ = 3/2. Therefore, the variance of X is given by:
σ²= ∫(x - μ)² * f(x) dx = ∫(x - 3/2)² * 3 dx (0 < x < 1).
On integrating, we get:σ²= [x³/3 - 3/2 * x² + 27/8 * x]₀¹= (1³/3 - 3/2 * 1² + 27/8 * 1) - (0³/3 - 3/2 * 0² + 27/8 * 0)= 1/3 - 3/2 + 27/8= 7/24. The variance of X is 7/24.
Learn More About Expected Value and Variance: https://brainly.com/question/15858152
#SPJ11
a = 17.6 cm, b = 9.5 cm and c = 13.6 cm for the triangle shown below.
Answers
Answer: Click on this: a=13.6cm,b=9.5cm and c=2.6cm for the triangle show it has a step by step way
Step-by-step explanation:
has to be as a fraction help plzz

Answers
Hope this helps ;)
Determine the value of "z" in the equation
z + (14 - 5i) = 9 + 2i
Answers
Answer:
z = − 5 + 7i
Step-by-step explanation:
z + 14 - 5i = 9 + 2i
Subtract 14 from both sides.
z - 5i = 9 + 2i -14
Subtract 14 from 9 to get -5.
z - 5i = -5 +2i
Add 5i to both sides.
z = -5 + 2i + 5i
Combine real and imaginary parts.
z = -5 + (2+5)i
Add 2 to 5.
z = -5 + 7i
Hope this helps!
Answer:
7i - 5
Step-by-step explanation:
z + (14 - 5i) = 9 + 2i
=> z + 14 - 5i = 9 + 2i
=> z = 9 + 2i + 5i - 14
=> z = 7i - 5
Determine if each set of ordered pairs represents a function.

Answers
Answer:
h is the a
Step-by-step explanation:
Question 3
Use the coordinate plane. Write an ordered pair to represent the location of the point. Then identify the quadrant in or axes on which the
point is located.
Point D
A
-2
C
Next Question
Ay
-2
-10
-1
2
D
1 2 x
B
Laxis
Check Answer
©2023 McGraw Hill All Rights Reserved. Privacy Center Terms of Use Minin
Requirements Platform Status Center
Answers
Answer:
d
Step-by-step explanation:
d
viola drives 200 meters up a hill that makes an angle of 9 with the horizontal to th enearest tenth of a meter what horizontal distance has she coverrd
Answers
Viola covered approximately 33.7 meters horizontally while driving 200 meters up a hill that makes an angle of 9 degrees with the horizontal. This can be calculated using trigonometry.
In a right triangle where one angle is 9 degrees and one side is 200 meters (the hypotenuse), the adjacent side (the horizontal distance covered by Viola) can be found by taking the tangent of the angle. The tangent of an angle is equal to the ratio of the length of the opposite side to the length of the adjacent side.
By multiplying the length of the hypotenuse (200 meters) by the tangent of the angle (tan(9)), we can find the length of the adjacent side, which is the horizontal distance covered by Viola. This calculation gives us approximately 33.7 meters.
Therefore, Viola drove 200 meters up the hill and covered approximately 33.7 meters horizontally to get to her destination.
Learn more about meters here:
https://brainly.com/question/29367164
#SPJ11
Which is the graph of the solution set of −2x + 5y > 15?
On a coordinate plane, a dashed straight line has a positive slope and goes through (0, 3) and (10, 7). Everything above and to the left of the line is shaded.
On a coordinate plane, a dashed straight line has a negative slope and goes through (0, 3) and (5, 1). Everything below and to the left of the line is shaded.
On a coordinate plane, a dashed straight line has a positive slope and goes through (0, 5) and (10, 9). Everything above and to the left of the line is shaded.
Answers
Answer:
it is the first option
Step-by-step explanation:
First step. Switch the greater than sign and turn the linear inequality to slope formula. after that graph the line. it is a dashed line due to not being greater than EQUAL to. if not equaled to then it is dotted. then you need a point as your testing point to see if it is shaded in that area. I chose to(0,0) but you could have chose any point. Once you plug in the zeros you will notice you get the false statement of 0 greater than 15. so obviously that is a no so you shade the opposite side of your testing point. phew
Answer:
A. On a coordinate plane, a dashed straight line has a positive slope and goes through (0, 3) and (10, 7). Everything above and to the left of the line is shaded.
Step-by-step explanation:
At your express they charge $0.17 per ounce for yogurt and toppings. Maria pays $2.04 for her yogurt. How many ounces of yogurt and toppings did Maria get
Answers
Practice question — Given the trapezoid to the right find the length of legs in the following isosceles trapezoid
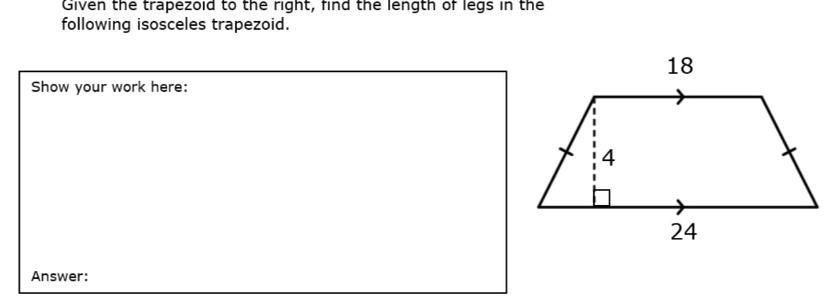
Answers
Given:
A figure of an isosceles trapezoid with bases 18 and 24, and the vertical height is 4.
To find:
The legs of the isosceles trapezoid.
Solution:
Draw another perpendicular and name the vertices as shown in the below figure.
From the figure it is clear that the AEFD is a rectangle. So,
\(EF=AD=18\)
Since ABCD is an isosceles trapezoid, therefore in triangle ABE and DCF,
\(AB=DC\) (Legs of isosceles trapezoid)
\(AE=DF\) (Vertical height of isosceles trapezoid)
\(m\angle AEB=m\angle DFC\) (Right angle)
\(\Delta ABE\cong \Delta DCF\) (HL postulate)
\(BE=CF\) (CPCTC)
Now,
\(BE+EF+FC=BC\)
\(2BE+18=24\)
\(2BE=24-18\)
\(2BE=6\)
\(BE=3\)
Using Pythagoras theorem in triangle ABE, we get
\(Hypotenuse^2=Perpendicular^2+Base^2\)
\((AB)^2=(AE)^2+(BE)^2\)
\((AB)^2=(4)^2+(3)^2\)
\((AB)^2=16+9\)
\((AB)^2=25\)
Taking square root on both sides, we get
\(AB=\pm \sqrt{25}\)
\(AB=\pm 5\)
Side length cannot be negative. So, \(AB=5\).
Therefore, the length of legs in the given isosceles trapezoid is 5 units.

PLEASE HELP *URRRRGGEEEENTTTTTT*
Identify the meaning of the following word in the sentence below:
The dog’s temperament was perfect for my son.
a.
height
c.
physical and mental character;mood
b.
weight
d.
color; contrast
Answers
Answer:
c
Step-by-step explanation:
Temperament is to do with the personality of someone.
Thus the dog's temperament would relate to its physical and mental character.
c
Temperament is to do with the personality of someone.
Thus the dog's temperament would relate to its physical and mental character.
In one U.S. city, the taxi cost is $5 plus $0.70 per mile. If you are traveling from the airport, there is an additional charge of 6$ for tolls. How far can you travel from the airport by taxi for $39?
Answers
Answer:
47 miles
Step-by-step explanation:
first subtract 6 from 39 and divide the remainder by 0.7. Round to 47 for answer.
(9p-5q)^2=can anyone plss answers this
Answers
Step-by-step explanation:
\( {(9p - 5q)}^{2} \)
Hence according to ,
\( {(a - b)}^{2} = {a}^{2} - 2ab + {b}^{2} \)
So,
\( {(9p)}^{2} - 2 \times 9p \times 5q + {(5q)}^{2} \)
\(81 {p}^{2} - 90pq + 25 {q}^{2} (ans)\)
What is the value of x?

Answers
Answer:
141°
Step-by-step explanation:
The sum of the internal angles can be calculated using the following formula:
(number of sides - 2) x 180°
This polygon has 7 sides, so (7 - 2) x 180° = 900° total internal angle.
Subtract the other given angles from 900°.
(900 - 131 - 122 - 125 - 148 - 107 - 126)° = 141°
Answer:
x equals 141°
Step-by-step explanation:
The sum of interior angles of this figure is 900°. This was found using the formula (n-2) x 180 where 'n' means number of sides. This figure has 7 sides. So the sum of interior angles would be:-
(7 - 2) x 180°
5 x 180°
= 900°
All the given angles + x gives 900°.
So, to find 'x' we can do the following:-
148° + 125° + 122° + 131° + x° + 126° + 107° = 900°
759 + x = 900
x = 900 - 759
x = 141°
HELP......................! !

Answers
Answer:
-9 7/15
Step-by-step explanation:
all of the digits of a three-digit integer are distinct and non-zero. furthermore, the three-digit integer is divisible by each of its digits. find the largest three-digit integer that has these properties.
Answers
The largest three-digit number satisfying the given criteria is 964.
Given that all the digits of a three-digit integer are distinct and non-zero.
Further more, the three-digit integer is divisible by each of its digits.
We are to find the largest three-digit integer that has these properties.
What we know: We know that a number is divisible by its digit if and only if the number is divisible by the least common multiple of the digits of the number.
Since all the digits are distinct and non-zero, the least common multiple of the digits of the number is simply the product of the digits.
Let's assume the number to be a b c,
where a, b, and c represent digits of the three-digit integer.
We are required to find the largest such number satisfying the given criteria.
Since the number must be divisible by each of its digits, it follows that each digit must be a factor of the number.
Hence, we can write,
a b c = a x b x c
The number must be greater than 100.
Hence, a must be at least 1. b and c must be distinct from a and from each other.
Hence, the smallest possible value for b is 2, and for c is 3.
This gives us the following equations: 123 = 1 x 2 x 3124
= 1 x 2 x 4125
= 1 x 2 x 5126
= 1 x 2 x 6128
= 1 x 2 x 8129
= 1 x 2 x 9
For similar question on least common multiple
https://brainly.com/question/16054958
#SPJ11
A bouquet of flowers has pink roses, red roses and yellow tulips. The probability of selecting a pink rose is 14. What is the probability of not selecting a pink rose?
Answers
Answer:
\(\dfrac{3}{4}\)
Step-by-step explanation:
Given an event A
The probability of A occurring + The probability of A not occurring=1
or we can say:
P(A)+P(\(A^c\))=1, where \(A^c\) is the complement of A.
In the given problem, if the probability of selecting a pink rose is 1/4.
(I want to presume its 1/4 not 14 since probability cannot be greater than 1)
We then have:
P(selecting a pink rose) + P(not selecting a pink rose)=1
P(not selecting a pink rose)=1-P(selecting a pink rose)
\(=1-\dfrac{1}{4}\\\\=\dfrac{3}{4}\)
17. Sally put $960 in a savings account that earns 7% interest compounded quarterly. How much interest will she earn at the end of the thrid quarter? What will be her account balance at that time?
Answers
well, one quarter of a year is 3 months, so at the end of third quarter, 9 months have passed, and since a year has 12 months, 9 months are simply 9/12 of a year.
\(~~~~~~ \textit{Compound Interest Earned Amount} \\\\ A=P\left(1+\frac{r}{n}\right)^{nt} \quad \begin{cases} A=\textit{accumulated amount}\\ P=\textit{original amount deposited}\dotfill &\$960\\ r=rate\to 7\%\to \frac{7}{100}\dotfill &0.07\\ n= \begin{array}{llll} \textit{times it compounds per year}\\ \textit{quarterly, thus four} \end{array}\dotfill &4\\ t=years\to \frac{9}{12}\dotfill &\frac{3}{4} \end{cases}\)
\(A=960\left(1+\frac{0.07}{4}\right)^{4\cdot \frac{3}{4}}\implies A=960(1.0175)^3\implies A\approx 1011.29\)
7. You order two sandwiches and a drink. The drink costs $1.50. You pay 6% sales tax and leave a $3 tip. You
pay a total of $12.54. How much does one sandwich cost?
Answers
The drink costs $1.50. You pay 6% sales tax and leave a $3 tip. You
pay a total of $12.54.The sandwich cost is $34.1 .
Unless the transactions is exempt, every sale, entry, holding, or lease is taxable. The cost of taxable products or services is increased by the sales tax, which is then charged to the customer at the point of sale.
The right response for Bea's overall price is $34.92
$3.50 + $9.80 + $13.90, or $272, is the total cost of takeaway.
The current sales tax rate is 7%.
and Tip is 20%.
Sales Tax = $27.2 x 7%
$1.90 sales tax
Similar Tip = $5.84 of $27.2 Tip
Tip = $5.84 The overall cost is thus:
The overall cost is thus:
Given.
Price in total: $27.2 plus $1.90 Plus $5
A tax rate is the amount at which a company or individual is subject to tax. Tax rates can be shown in a variety of ways, including average, marginal, even effective.
To finance its operations, the government levies fees on citizens based on factors like their income, the worth of the property, etc.
Learn more about tax here:
https://brainly.com/question/1775528
#SPJ9
Thank you so very much for helping

Answers
Answer:
Angle 2
Step-by-step explanation:
They are 90 degrees when added together
Answer:
<2
Step-by-step explanation:
Complementary angles add to 90 degrees ( form right angles)
<1 and <2 add to 90 degrees so they are complementary angles
what is this answer?
7k-3k+11
Answers
Answer:
4k+11 is the answer
Step-by-step explanation:
7k-3k =4k
4k+11!
In each of the following cares, find the least square approximation of degrees 0,1 and 2 for the function f(x) = sin(x) on the interval (a,b) with respect to the weight function w(x) = 1. (a) (a,b) = (-7,7) (b) (a,b) = (-2,5)
Answers
The least square approximation of degree 2 for sin(x) on the interval over the function (-2, 5) is f(x) ≈ 0.223 + 0.394x + 0.090x².
To find the least square approximation of degree 0, we look for a constant function that best approximates sin(x) on the interval (a, b). Since the weight function is constant, the least square approximation of degree 0 is simply the average of the function values over the interval. Thus, for the interval (-7, 7), the least square approximation of degree 0 is:
a₀ = (1/(7-(-7))) ∫(-7)⁷ sin(x) dx = 0
Similarly, for the interval (-2, 5), the least square approximation of degree 0 is:
a₀ = (1/(5-(-2))) ∫(-2)⁵ sin(x) dx = 0.2778
To find the least square approximation of degree 1, we look for a linear function that best approximates sin(x) on the interval (a, b).
Solving this system of equations leads to the following coefficients for the interval (-7, 7):
a₀ = 5/14π ≈ 0.224 a₁ = 2/7π ≈ 0.452
Thus, the least square approximation of degree 1 for sin(x) on the interval (-7, 7) is f(x) ≈ 0.224 + 0.452x.
Thus, the least square approximation of degree 1 for sin(x) on the interval (-2, 5) is f(x) ≈ 0.2778 + 0.287x.
To find the least square approximation of degree 2, we look for a quadratic function that best approximates sin(x) on the interval (a, b). We represent the quadratic function as f(x) = a₀ + a₁x + a₂x² and find the coefficients a₀, a₁, and a₂ that minimize the sum of the squared differences between sin(x) and f(x) on the interval (a, b).
Solving this system of equations leads to the following coefficients for the interval (-7, 7):
a₀ ≈ -0.006 a₁ ≈ 0.999 a₂ ≈ 0.005
Thus, the least square approximation of degree 2 for sin(x) on the interval (-7, 7) is f(x) ≈ -0.006 + 0.999x + 0.005x².
Similarly, for the interval (-2, 5), the least square approximation of degree 2 is:
a₀ ≈ 0.223 a₁ ≈ 0.394 a₂ ≈ 0.090
To know more about function here
https://brainly.com/question/28193995
#SPJ4
Test if the slope significant for the next values. β1=0.0943 , seβ1=0.107 and alpha 0.05.
6. Write the null and alternative hypothesis. (2 points
7. Calculate t-test statistic 8. Write tc, degrees of freedom and decision rule. 9. Conclusion.
Answers
The null and alternative hypotheses are:
H0: β1 = 0 (The slope is not significant.)
H1: β1 ≠ 0 (The slope is significant.)
Here,β1=0.0943seβ1=0.107α=0.05
Test the slope significance and find the t-test statistic.
We need to find the t-test statistic so that we can compare it with the t-distribution, whose distributional properties we know, to determine if we can reject or fail to reject the null hypothesis.t-test statistic is calculated by dividing the value of β1 by its standard error (seβ1) and taking the absolute value of this quotient.
t-test statistic = | β1/seβ1 | = |0.0943/0.107| = 0.881
The degrees of freedom (df) associated with this t-test are df = n - 2, where n is the sample size for the explanatory variable x.
In this problem, the decision rule and conclusion are as follows:
Decision Rule: Reject the null hypothesis if |t-test statistic| > tc where tc is the critical value obtained from the t-distribution with df degrees of freedom and a significance level of α/2 in each tail.
Conclusion: The slope is not significant if we fail to reject the null hypothesis, but the slope is significant if we reject the null hypothesis. Since the t-test statistic (0.881) is less than the critical value (1.987), we fail to reject the null hypothesis. Therefore, we conclude that the slope is not significant.
To know more about null and alternative hypotheses:
https://brainly.com/question/33444525
#SPJ11
From the set {4, 8, 10}, use substitution to determine which value of x makes the equation true.
Answers
To use substitution to determine which value of x makes the equation true, we must first have an equation to substitute the values from the set {4, 8, 10} into.
If we don't have an equation, we can't use substitution.
It would be helpful if you could provide an equation to solve with the set {4, 8, 10}
maria bought a swimming pool with a circumference of 24 feet. she wants to buy a cover for her pool. what is the approximate size of the cover that maria will need to buy? round your answer to the nearest hundredth.
Answers
The approximate size of the cover that Maria will need to buy is 45. 84 square feet
How to determine the valueThe formula for calculating the circumference of a circle is expressed as;
Circumference = πr²
Where 'r' is the radius of the circle
Now, let's substitute the value of the circumference
24 = 2 × 3. 14 × r
r = 24/6. 28
r = 3. 82 feet
Formula for area = πr²
Substitute value of r
Area = 3. 14 × (3. 82)²
Area = 3. 14 × 14. 59
Area = 45. 84 square feet
Hence, the value is 45. 84 square feet
Learn more about area here:
https://brainly.com/question/25292087
#SPJ1
Trey's Coffee Shop makes a blend that is a mixture of two types of coffee. Type A coffee costs Trey $5.80 per pound, and type B coffee costs $4.25 per pound. This month, Trey made 142 pounds of the blend, for a total cost of $724.40. How many pounds of type A coffee did he use?
Answers
Using a system of equations, the quantity of Type A coffee that Trey's Coffee Shop blended with Type B coffee was 78 pounds.
What is a system of equations?A system of equations or simultaneous equations is two or more equations solved concurrently, simultaneously, or at the same time.
Unit Cost Per Pound:
Type A coffee = $5.80
Type B coffee = $4.25
The total quantity of pounds of the blend = 142 pounds
The total cost of 142 pounds = $724.40
Let the number of Type A coffee = x
Let the number of Type B coffee = y
Equations:x + y = 142 ... Equation 1
5.8x + 4.25y = 724.40 ... Equation 2
Multiply Equation 1 by 4.25:
4.25x + 4.25y = 603.5 ... Equation 3
Subtract Equation 3 from Equation 2:
5.8x + 4.25y = 724.40
-
4.25x + 4.25y = 603.5
1.55x = 120.9
x = 78
Substitute x = 78 in either equation:
x + y = 142
78 + y = 142
y = 64
Thus, 78 pounds of Type A coffee was used for the mixture.
Learn more about a system of equations at https://brainly.com/question/13729904.
#SPJ1
please help me this question

Answers
Answer: Choice D. (x/8) - 2 = 5
Work Shown:
x = Aatif's age
x/8 = divide the age by 8
(x/8) - 2 = divide the age by 8 first, then subtract off 2
(x/8) - 2 = 5 .... the previous result is equal to 5
A $0.25 \mathrm{~kg}$ stone is held $11 \mathrm{~m}$ above the top edge of a water well and then dropped in. The well has a depth of $7.3 \mathrm{~m}$. Taking $y=0$ at the top edge of the well, calculate
(a) the gravitational potential energy of the stone-Earth system before the stone is released
(b) the gravitational potential energy of the stone-Earth system after the stone reaches the bottom of the well
(c) the change in gravitational potential energy of the system from when the stone is released to when it reaches the bottom of the well.
Answers
The gravitational potential energy of the stone-Earth system can be calculated before the stone is released, after it reaches the bottom of the well, and the change in gravitational potential energy during the process.
Gravitational potential energy is given by the formula PE = mgh, where m is the mass of the object, g is the acceleration due to gravity, and h is the height.
(a) Before the stone is released, it is held 11 m above the top edge of the well. The mass of the stone is 0.25 kg, and the acceleration due to gravity is approximately 9.8 m/s². Using the formula, the gravitational potential energy is calculated as PE = (0.25 kg)(9.8 m/s²)(11 m).
(b) After the stone reaches the bottom of the well, its height is 7.3 m. Using the same formula, the gravitational potential energy at this point is given by PE = (0.25 kg)(9.8 m/s²)(7.3 m).
(c) The change in gravitational potential energy can be determined by subtracting the initial potential energy from the final potential energy. The change in gravitational potential energy is equal to the gravitational potential energy after reaching the bottom of the well minus the gravitational potential energy before the stone was released.
By calculating these values, we can determine the specific numerical values for (a), (b), and (c) based on the given data.
Learn more about gravitational here:
https://brainly.com/question/32609171
#SPJ11