Joan had 382 apples to divide among 33 bags. If she gave an even
amount to each bag, how many will she have left? *
1 point
Your answer
This is a required question
Answers
Answer:
19
Step-by-step explanation:
382 can be divided 33 ways to give 11 apples in each bag with a remainder of 19 apples.

Related Questions
solve for r 5(r-10)= -51
Answers
Answer:
r= -1/5
Step-by-step explanation:
Step 1: Remove the parentheses (5r-10= -51)
Step 2: Move the constant to the right-hand side and change the sign (5r= -51 + 50)
Step 3: Calculate the sum of -51 +50 (5r = -1)
Last Step: Divide both sides by the equation by 5 (r = -1/5)
The solution for r in the equation is -1/5
The equation given is 5(r-10)= -51
To solve this question, use the distributive property. The distribute property entails expanding the terms in the bracket. This means multiply the terms in the bracket by 5
5(r - 10)
= 5 x (r - 10)
= 5r - 50
The equation then becomes : 5r - 50 = -51
The second step is to combine similar terms. This would be done by making use of the additive property of equalities: 50 would be added to both sides of the equation
5r = -51 + 50
5r = -1
The third step is to divide both sides of the equation by 5
(5r / 5) = (-1 /5)
r = -1/5
A similar question was solved here : https://brainly.com/question/17224218
If
�
1
=
8
a
1
=8 and
�
�
=
−
3
�
�
−
1
−
2
a
n
=−3a
n−1
−2 then find the value of
�
5
a
5
.
Answers
The value of a₅ is 688. The problem provides us with a recursive formula that relates each term of the sequence to the previous term.
We can use this formula to find the value of any term in the sequence, given the value of the previous term.
The recursive formula is:
aₙ = -3aₙ₋₁ - 2
This formula tells us that to find the value of aₙ, we need to take the previous term aₙ₋₁, multiply it by -3, and then subtract 2.
The problem also provides us with the value of the first term a₁, which is 8. Using the recursive formula, we can find the value of the second term a₂:
a₂ = -3a₁ - 2 = -3(8) - 2 = -26
We can repeat this process to find the value of the third term a₃:
a₃ = -3a₂ - 2 = -3(-26) - 2 = 76
Continuing in this manner, we can find the values of a₄ and a₅:
a₄ = -3a₃ - 2 = -3(76) - 2 = -230
a₅ = -3a₄ - 2 = -3(-230) - 2 = 688
Therefore, the value of a₅ is 688.
To learn more about recursive please click on below link.
https://brainly.com/question/30027987
#SPJ1
If a₁ = 8 and aₙ = -3aₙ₋₁ - 2, then what is the value of a₅?
A ramp is 16ft long rises to a platform that is 12ft off the ground, find X, the angle of elevation of the ramp. Round your answer to the nearest tenth of a degree
Answers
Answer:
x = 48.6°
Step-by-step explanation:
see photo for explanation
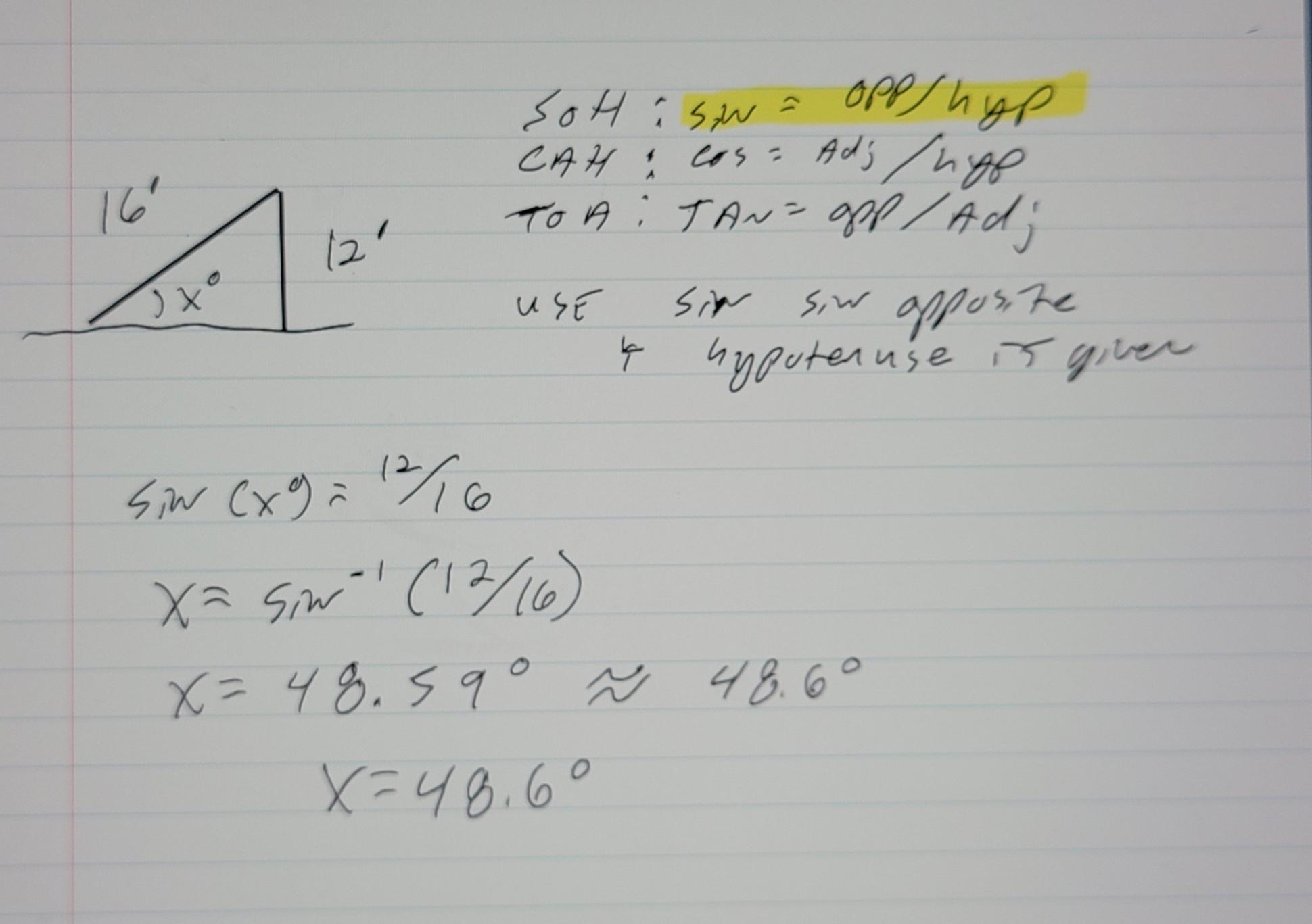
the population p of bacteria in an experiment grows according to the equation where k is a constant and t is measured in hours. if the population of bacteria doubles every 24 hours, what is the value of k ?
Answers
If the population of bacteria doubles every 24 hours, then the value of k is 0.029.
In the given question;
If the population of bacteria doubles every 24 hours, then we have to find the value of k
Given: Differential equation for the population is dp/dt=kp ; where t = hours.
Apply integration on both sides
dp/dt=kp
dp/p=kdt
∫1/p *dp =∫kdt
Inp=k∫1dt
Inp=kt+c …(i)
Let the population at t=0(i.e. initially) be p(0)
Then from equation (i):
For t=0,p=p(0)
Inp(0)=k(0)+c
Inp(0)=c
Put ‘c’ in equation (i), then:
Inp=kt+ Inp(0)
Inp-Inp(0)=kt
In(p-p(0))=kt
(∴ Since loga-logb=log(a/b))
In(p/p(0))=kt …(ii)
Given the population doubles for every 24 hours
i.e. for t=24 hours, p=2p(0)
∴put the value of t=24 & p=2p(0)
Equation (ii)
In(p/p(0))=kt
In(2p(0)/p(0))=24k
In2=24k
k=In2/24
k=0.69314/24
k=0.02888
k=0.029
The value of ‘k’ is 0.029.
To learn more about Differential equation link is here
brainly.com/question/14598404
#SPJ4
A television network wanted to estimate the proportion of a one-hour time slot that is made up of commercials. The network took random samples of
10
10 one-hour time slots. The following are the sample proportions the network found in
12
12 samples.
Part A
What is the estimated proportion of commercials in all one-hour time slots? Round your answer to the nearest thousandth.
Answers
Answer:
120
Step-by-step explanation:
Remember, always round sample size up, regardless of the decimal part. Answer: To find a 95% CI with a margin of error no more than ±3.5 percentage points, where the true population proportion is around 42%, you must survey at least 764 people. 10×764 = 7640; presumably the electorate is larger than that. So, then 10 × 12 = 120
On her way to her grandmother's house, Jackie traveled three times as many miles by train as by bus. She traveled four times as many miles by bus as by foot. If Jackie traveled 34 miles in all, how many miles did she travel by train?
Answers
Answer:
15
Step-by-step explanation:
Answer:15
Step-by-step explanation:
Anyone know how to do this?

Answers
An angle bisector theorem is used to determine AD = 4.68 as the length of the side of the triangle AD.
What is the angle bisector theorem explained?Vertex, the intersection of two lines, is used to measure angles. Internal angles are created by the sides of geometric shapes like triangles and rectangles.
Each geometric figure has a general dimension determined by the sum of its interior angles. Geometrical operations such as bisecting an angle are possible.Each angle that also is bisected is divided into two angles of equal size. The bisector is constructed from the vertex defining the principal angle.With the triangles that are presented, prove the angle bisector theorem:
There will be equality in the side ratios.
AB / BC = AD / DC
AB = 9 ; BC = 11.7 AD = 3.6
Put the values.
9/11.7 = 3.6 / AD
AD = 3.6*11.7 / 9
AD = 4.68
Thus, an angle bisector theorem is used to determine AD = 4.68 as the length of the side of the triangle AD.
Know more about the angle bisector theorem
brainly.com/question/9742008
#SPJ1
determine a region whose area is equal to the given limit. do not evaluate the limit.
Answers
The obtained limit is identical to the limit that was specified. Therefore, the right answer is option C.
What is a region whose area is equal to the given limit?Generally, the equation for the limit is mathematically given as
\($\lim _{n \rightarrow \infty} \sum_{i=1}^{n} \frac{4}{n} \sqrt{1+\frac{4 i}{n}}$.\)
The goal is to locate the zone whose area corresponds to the value supplied by the limit.
The definite integral of a function is what is used to compute the area of that function that is underneath its graph.
The limit,
\(\lim _{n \rightarrow \infty} \sum_{i=1}^{n} f(a+i \cdot \Delta x) \Delta x\)
where\($\Delta x=\frac{b-a}{n}$\) and \($x_{i}=a+i \Delta x$\) for the interval $[a, b]$, is equivalent to the integral
\(\int_{a}^{b} f(x) d x .\)
The given limit can also be written as
\(\lim _{n \rightarrow \infty} \sum_{i=1}^{n} \sqrt{1+\left(\frac{4}{n}\right)} i \cdot \frac{4}{n} .\)
In this limit, \($\Delta x=\frac{4}{n}$\). It can be observed that\($f(a+i \Delta x)=\sqrt{1+\left(\frac{4}{n}\right)} i$\) which implies that \($a=1$ and $f(x)=\sqrt{x}$.\)
Solve the \($\Delta x=\frac{b-a}{n}$\)equation for as follows:
\(\begin{aligned}\frac{4}{n} &=\frac{b-1}{n} \\4 &=b-1 \\5 &=b\end{aligned}\)
Therefore, the specified limit may be expressed as an integral as follows:
\(\lim _{n \rightarrow \infty} \sum_{i=1}^{n} \sqrt{1+\left(\frac{4}{n}\right) i} \cdot \frac{4}{n}=\int_{1}^{5} \sqrt{x} d x\)
Therefore, the limit that has been provided designates the area of the graph of "sqrt(x)" on the interval.[1,5]
However, none of the available choices are compatible with this choice. So, consider
\(a=0, f(x)=\sqrt{1+x}$ and $\Delta x=\frac{4}{n}$.\)
Find the value of $b$ as:
\($$\begin{aligned}\frac{4}{n} &=\frac{b-0}{n} \\4 &=b\end{aligned}$$\)
Find the value of x_{i} as:
\(\begin{aligned}&x_{i}=0+\frac{4}{n} i \\&x_{i}=\frac{4}{n} i\end{aligned}\)
$$
Thus, the integral \($\int_{0}^{4} \sqrt{1+x} d x$\) can be expressed using the equation \($\int_{a}^{b} f(x) d x=\lim _{n \rightarrow \infty} \sum_{i=1}^{n} f\left(x_{i}\right) \Delta x$\)
\(\begin{aligned}\int_{0}^{4} \sqrt{1+x} d x &=\lim _{n \rightarrow \infty} \sum_{i=1}^{n} \sqrt{1+\frac{4 i}{n} \frac{4}{n}} \\&=\lim _{n \rightarrow \infty} \sum_{i=1}^{n} \frac{4}{n} \sqrt{1+\frac{4 i}{n}}\end{aligned}\)
In conclusion, The obtained limit is identical to the limit that was specified. Therefore, the right answer is option C.
Read more about region
https://brainly.com/question/13162113
#SPJ4
CQ
The complete Question is attached below

the supervisor of a call center would like to assemble a committe of 8 people from a staff of 15 call center agents. how many diffrent comittes can be chosen
Answers
Supervisor can choose 6435 different such 8 people committees from 15 call center agents.
We know that we can choose ' r ' number elements or persons from ' n ' number of elements or persons respectively in C(n, r) ways if we do not replace once chosen elements.
Here the total number of staff of call center agent is = 15
So n = 15.
And supervisor of the call center has to choose 8 agents from that group of 15 agents.
So, here r = 8.
Here as supervisor chooses a person he or she cannot be selected as two people.
So the event is without replacement.
Thus by the combination formula, the number of different such committees can be chosen by supervisor is = C(15, 8) = 6435.
Hence, supervisor can choose 6435 different such 8 people committees from 15 call center agents.
To know more about combination formula here
https://brainly.com/question/30806372
#SPJ4
n2 + n = 56 solution
Answers
Answer:
n = -8, 7
Step-by-step explanation:
Your equation is:
\(\displaystyle{n^2+n=56}\)
Arrange the terms in the quadratic expression, ax² + bx + c:
\(\displaystyle{n^2+n-56=0}\)
Factor the expression, thus:
\(\displaystyle{\left(n+8\right)\left(n-7\right)=0}\)
This is because 8n-7n = n (middle term) and 8(-7) = -56 (last term). Then solve like a linear which results in:
\(\displaystyle{n=-8,7}\)
Hello!
\(\sf n^2 + n = 56\\\\n^2 + n - 56 = 0\\\\\\n = \dfrac{-b\±\sqrt{b^2-4ac} }{2a} \\\\\\n = \dfrac{-1\±\sqrt{1^2-4*1*(-56)} }{2*1}\\\\\\n = \dfrac{1\±15}{2} \\\\\\\boxed{\sf n = 7 ~or ~-8 }\)
Which of the following experimental designs will create probabilities that vary the most from their theoretical probabilities?
Answers
The experimental design that will create probabilities that vary the least from their theoretical probabilities is option B: Flip a coin 5 times and record the number of tails that occur.
When conducting probability experiments, the Law of Large Numbers states that as the number of trials increases, the experimental probabilities will approach the theoretical probabilities more closely. However, this convergence to the theoretical probabilities occurs more rapidly when the number of trials is larger.
In options A, C, and D, the number of coin flips is significantly larger (500, 5000, and 50, respectively) compared to option B, which only involves 5 coin flips. As a result, options A, C, and D are more likely to exhibit greater variation from the theoretical probabilities.
With only 5 coin flips in option B, the outcomes may deviate from the expected probabilities due to the small sample size. However, as the number of flips increases, the experimental probabilities will converge more closely to the theoretical probabilities. Consequently, option B is expected to have probabilities that vary the least from their theoretical values among the given options.
It is worth noting that although option B will have less variation from theoretical probabilities compared to the other options, there may still be some variation due to random chance inherent in the coin flipping process.
For more such questions on tails
https://brainly.com/question/29151030
#SPJ8
Solve each system of equations algebraically. y=x + 15, y= 2x
Answers
The solution to the system of equations is (15, 30).
What is system of equations?A group of two or more equations that must be solved all at once is known as a system of equations. The system's equations each show how two or more variables relate to one another. The variables' values that satisfy every equation in the system can be discovered using algebraic techniques.
Algebraic systems of equations can be solved using a variety of techniques, such as substitution, elimination, and graphing. The substitution approach involves solving one equation for one variable in terms of the other variable, and then substituting the result for that variable's expression into the other equation.
The given system of equations are y=x + 15, y= 2x.
Substitute the value of y from equation 2 in equation 1:
x + 15 = 2x
15 = x
Substitute the value of x to get the value of y:
y = 2x = 2(15) = 30
Hence, the solution to the system of equations is (15, 30).
Learn more about system of equations here:
https://brainly.com/question/13760328
#SPJ1
2] The band has a ratio of boys to girls of 5 to 4. There are 52 girls in the band.
(Make sure to write out in words first.)
How many are boys?
How many total students?
I need work for both
Answers
Answer:
Step-by-step explanation:
For every 4 boys there are 5 girls and 9 students at the school. So that means that 49 of the students are boys. 49 of the total number of students is 120 students:
49×?=120
If 49 the number of students is 120, then 14 of 120 is 19 of the total number of students. In other words, 14×120=30 is 19 the total number of students. Then 9 times this amount will give the total number of students:
9×30=270
So there is a total of 270 students at the school. Note that this is equivalent to finding the answer to the division problem:
120÷49=?
We can see all of this very succinctly by using a tape diagram:
Bar_diagram_67722d3e6005449e4fbe5c57eaad4f3c
There are 4 units of boys and 9 units of students. Therefore 4/9 of the students are boys.
4 units = 120
1 unit = 30
9 units = 270
There are 270 students altogether.
Students can multiply the numbers in the first row by 10 to get the second row, and then double that amount to get the third row. Adding the entries in the second and third row gives the fourth row that has the solution.
Alternatively, since 120÷4=30, students can just multiply the numbers in the first row by 30 to get the values in the fourth row.
In every row, we can see that the fraction of the students that are boys is 49.
looking at the last row, we can see that the total number of students will be 4×30+5×30=120+150=270.
A rock that has been significantly reshaped on multiple surfaces by windborne particles and sometimes has a sharp edge is a(n) ________.
Answers
A rock that has been significantly reshaped on multiple surfaces by windborne particles and sometimes has a sharp edge is a(n) ventifact:
What is a rock?A rock refers to the solid portion of the earth crust which contains minerals. There are three types of rocks; The sedimentary rock: They are formed from dead plants, dead animals, sand etc.
The metamorphic rock: They are formed from previously existing rocks. The igneous rock: They are formed from the solidification of the molten magma.
Hence, ventifact are rock that has been significantly reshaped on multiple surfaces by windborne particles and sometimes has a sharp edge.
Read more on rocks:
https://brainly.com/question/25846908
#SPJ4
What is the solution to this system of linear equations?
y − 4x = 7
2y + 4x = 2
(3, 1)
(1, 3)
(3, −1)
(−1, 3)
Answers
Fatoumata has a deck that measures 7 feet by 12 feet. She wants to increase each
dimension by equal lengths so that its area is increased by 50%. By how much should she increase each dimension?
Answers
Based on common factors, Fatoumata can increase each dimension of the deck by 2 feet so that the deck's new area is increased by 50% to 126 ft².
What are common factors?Common factors are the numbers that can divide another number evenly without a remainder.
In this situation, 9 and 14 can divide 126 equally and the product of 9 and 14 are 126.
The old dimensions of the deck:
Width = 7 feet
Length = 12 feet
Area = 84 ft² (7 x 12)
The expected new area of the deck:
Increase in the new area = 5%
Increased factor for the area = 1.5 (100% + 50%)
Area = 126 ft² (84 x 1.5)
The common factors of 126 include 9 and 14 and the product of 9 and 14 = 126.
Therefore, we can increase each length of the deck by 2 feet.
Check:
Width = 9 feet
Length = 14 feet
Area = 126 ft² (9 x 14)
Learn more about common factors at https://brainly.com/question/219464.
#SPJ1
Find the value of MN if AB = 9 cm, BC = 7.2 cm, and LM = 12 cm.

Answers
Answer:
the answer is 9.6 cm
Step-by-step explanation:
.........................
A circle has a circumference of 20π meters. If a sector has a central angle of 45°, what is the arc length of the sector? Use pi = 3.14
Answers
the arc length of the sector is 7.85 meters.
Define circumferenceThe circumference is define for a circle is given by the formula:
C = 2πr
where C is the circumference, π is the value of pi, and r is the radius of the circle.
In this case, the circumference of the circle is given as 20π meters. So we can write:
20π = 2πr
Dividing both sides by 2π, we get:
r = 10 meters
The arc length of a sector of a circle with central angle θ and radius r is given by the formula:
Arc length = (θ/360°) x 2πr
where θ is the central angle in degrees.
In this case, the central angle of the sector is 45°, and the radius of the circle is 10 meters. So we can substitute these values into the formula:
Arc length = (45/360) x 2π(10) = (1/8) x 20π = 2.5π
Using the value of pi as 3.14, we can calculate the arc length as:
2.5π = 2.5 x 3.14 = 7.85 meters
Therefore, the arc length of the sector is 7.85 meters.
To know more about radius, visit:
https://brainly.com/question/13449316
#SPJ1
Can you pls help me with this

Answers
Answer:
c = 49
Step-by-step explanation:
A perfect square trinomial is of the form (x + a)²
If we expand (x + a)² we get:
x² + 2ax + a²
Compare this to the specific equation given:
x² + 2ax + a²
x² + 14x + c
Comparing like terms in both equations:
2ax = 14x ==> 2a = 14 ==> a = 14/2 = 7
Therefore a² = 7²
= 49
and this must be the value of c in the equation
Therefore c = 49
Plslslsllslslslslslslsl helppp

Answers
Answer:
BE = 39/5 or 7.8
Step-by-step explanation:
As <ABC = <DBE trigonometric function is angle BAC and angle BED
so sin (<ABC) = sin(<DBE) and AC and BC , BD and BE
so AC/AB = DE/BE = 13/BE = 5/3
So now we cross multiply
BE = 13 × 3 over 5
13 × 3 = 39
and over 5 means
39/5 = 7.8
(-11)+(-7)+(-3)0 -150-70 -21O 15
Answers
We need to know that when we are adding a negative number, is the same as subtracting that number.
So:
\(-11-7-3\)Now, we simply add negative numbers:
\(-21\)Correct option: number 3 = -21
Use the properties of the natural logarithm to expand each logarithmic expression. Round answers to 3
decimal places, if necessary. a. In(7x) = Preview 5x b. In Preview x + 3 c. In (x 8) = Preview d. 15,000 In(xy4) =
Answers
a. ln(7x) can be expanded as ln(7) + ln(x). b. ln(x + 3) remains as it is, since it cannot be simplified further. c. ln(x^8) can be expanded as 8ln(x). d. 15,000ln(xy^4) can be expanded as ln(x) + 4ln(y) + ln(15,000).
a. To expand the logarithmic expression ln(7x), we can use the property of the natural logarithm that states ln(ab) = ln(a) + ln(b).
Therefore, ln(7x) can be expanded as ln(7) + ln(x).
b. Similarly, the logarithmic expression ln(x + 3) can be expanded using the property ln(ab) = ln(a) + ln(b).
Hence, ln(x + 3) remains as it is since we cannot simplify it further.
c. Expanding the logarithmic expression ln(x^8) can be done using the property ln(a^b) = b * ln(a).
Thus, ln(x^8) becomes 8 * ln(x).
d. Expanding the logarithmic expression 15,000ln(xy^4) can be done by applying the property ln(ab) = ln(a) + ln(b).
Therefore, 15,000ln(xy^4) can be expanded as 15,000[ln(x) + ln(y^4)].
Learn more about expanded here
https://brainly.com/question/17921963
#SPJ11
the growth curve shown depicts growth projections for a single population. a graph plots population size on the y axis and time on the x axis. an exponential curve shows slow population growth at first and then rapid increase over time. what would happen if the birth rate were to decline?
Answers
If the birth rate were to decline in a population, the growth curve would be affected as well. A decrease in the birth rate would cause the population growth to slow down, resulting in a change in the shape of the curve.
Initially, the exponential curve illustrates slow population growth, followed by a rapid increase over time. However, with a declining birth rate, the curve would likely transition into a logistic growth curve. This type of curve is characterized by an initial period of slow growth, followed by a phase of rapid growth, and eventually leveling off when the population reaches its carrying capacity or other limiting factors come into play.
The projections for the population growth would also be impacted by the decrease in the birth rate. Lower birth rates typically lead to slower growth rates, and in some cases, may even result in a population decline if the birth rate falls below the death rate. This change would be reflected in the updated projections for population growth over time.
In summary, if the birth rate were to decline in a population with an exponential growth curve, the curve would likely shift towards a logistic growth pattern, with slower overall growth and eventual leveling off. The projections for population growth would need to be adjusted to account for the changes caused by the reduced birth rate.
learn more about population growth here: brainly.com/question/27779235
#SPJ11
$
A water tank in the shape of a cuboid has length 1.5 metres and width 1 metre.
The water in the tank is 60 centimetres deep.
Calculate the number of litres of water in the tank.
Answers
We can write the volume of the water in the water tank is 9/10 cubic meters.
What is the volume of a cuboid?The volume of a cuboid is given by -
V = Length x Width x Height
V = L x W x H
Given is that a water tank in the shape of a cuboid has length 1.5 meter's and width 1 meter. The water in the tank is 60 centimeters deep.
We can write the volume of the water tank as -
V = Length x Width x Height
V = L x W x H
V = 1.5 x 1 x (60/100)
V = 1.5 x 3/5
V = 3/2 x 3/5
V = 9/10 cubic meters
Therefore, we can write the volume of the water in the water tank is 9/10 cubic meters.
To solve more questions on volume, visit the link-
https://brainly.com/question/22907480
#SPJ9
If b=24 and c=10 what is for the missing side a= ? by Use the Pythagorean Theorem to find.
Answers
Answer:
a = 26
a ~ 21.8
Read explanation
Step-by-step explanation:
There are two possibilities;
\(a^{2}+c^{2}=b^{2}\)
Or
\(b^{2}+c^{2}=a^{2}\)
This is because one doesn't know the longest side, and hence there are two possibilities as to what the longest side is.
1. \(a^{2}+c^{2}=b^{2}\)
Substitute in the given values;
\(a^{2}+(10)^{2}=(24)^{2}\)
\(a^{2}+100=576\)
\(a^{2}=476\)
a=\(\sqrt{476}\)
a~21.8
2.\(b^{2}+c^{2}=a^{2}\)
Substitute in the given values;
\((24)^{2}+(10)^{2}=a^{2}\)
\(576+100=a^{2}\)
\(676=a^{2}\)
\(26=a\)
aldosterone stimulates the reabsorption of sodium while enhancing potassium secretion.
a. true b. false
Answers
I believe that may be false
Answer:
Step-by-step explanation:
True.
Aldosterone is a hormone produced by the adrenal gland that plays an important role in regulating electrolyte and water balance in the body. It acts on the cells of the distal tubules and collecting ducts of the kidneys to increase the reabsorption of sodium ions and the secretion of potassium ions.
This helps to increase blood volume and blood pressure by retaining more sodium and water in the body while getting rid of excess potassium. Aldosterone release is regulated by the renin-angiotensin-aldosterone system, which is activated in response to low blood pressure or low sodium levels in the blood.
know more about Aldosterone: brainly.com/question/31670445
#SPJ11
A cylindrical Paint storage tank is 8 feet high and has a radius of 3 feet. What is the maximum volume of Paint that can be stored in the
tank?
Answers
Answer:
Step-by-step explanation:
The maximum volume of paint that can be stored in the cylindrical tank occurs when it is completely filled. The formula for the volume of a cylinder is:
V = πr^2h
where V is the volume, r is the radius, and h is the height.
In this case, the height of the cylindrical tank is 8 feet and the radius is 3 feet. So we can substitute these values into the formula to get:
V = π(3^2)(8)
V = π(9)(8)
V = 72π
Therefore, the maximum volume of paint that can be stored in the tank is 72π cubic feet, which is approximately 226.2 cubic feet if we round to one decimal place.
(Solving Equations Using Square and Cube Roots LC)
Solve y3 = −1.
y = −0.5
y = 0.5
y = −1
y = ±1
Answers
Answer:
Step-by-step explanation:
J Square Roots and Cube Roots To find the square root of a number, you want to find some number that when multiplied by itself gives you the original number. In other words, to find the square root of 25, you want to find the number that when multiplied by itself gives you 25. The square root of 25, then, is 5. The symbol for square root is equation.
What are the x-intercept(s) of the function the quantity of 5 x squared minus 25 x, all over x? x = 5 x = 0 and x = 5 x = 0 x = −5
Answers
The value of x will be 0 and x = 5. The correct option is A.
What is the x-intercept?The x-intercept is the point at which a line intersects the x-axis, and the y-intercept is the point at which the line intersects the y-axis.
Mathematical symbols can be used to represent numbers (constants), variables, operations, functions, brackets, punctuation, and grouping. They can also denote the logical syntax's operation order and other properties.
Given that the x-intercept(s) of the function is the quantity of 5x² - 25x.
The value of the x-intercept will be calculated as,
5x² - 25x = 0
5x( x -25) = 0
5x = 0 and x - 5 = 0
x = 0 and x = 5
Therefore, the value of x will be 0 and x = 5. The correct option is A.
To know more about x-intercept follow
https://brainly.com/question/17932786
#SPJ1
Answer:
it's x = 5
Step-by-step explanation:
got it right on the test.
.A key concept in agile projects is that something of value will be delivered at each iteration.
True or false?
Answers
Answer:
Step-by-step explanation:
Which statements about the relationship between the two triangles below are true? Check all that apply.Mark this and return