Let A = {1, 2, 3, 4, 5, 6, 7} and B = {4,5,6,7,8,9,10). The universal set for this problem is U = {1,2,3,..., 13}. (a) List the elements in A - B. (b) List the elements in B - A.
Answers
a. A - B = {1, 2, 3}. b. B - A = {8, 9, 10}. The elements that are in A but not in B.
a) To find the elements in A - B (set difference of A and B), we need to list the elements that are in A but not in B.
A = {1, 2, 3, 4, 5, 6, 7}
B = {4, 5, 6, 7, 8, 9, 10}
Elements in A - B: {1, 2, 3}
Therefore, A - B = {1, 2, 3}.
b) To find the elements in B - A (set difference of B and A), we need to list the elements that are in B but not in A.
Elements in B - A: {8, 9, 10}
Therefore, B - A = {8, 9, 10}.
Learn more about elements here
https://brainly.com/question/25916838
#SPJ11
Related Questions
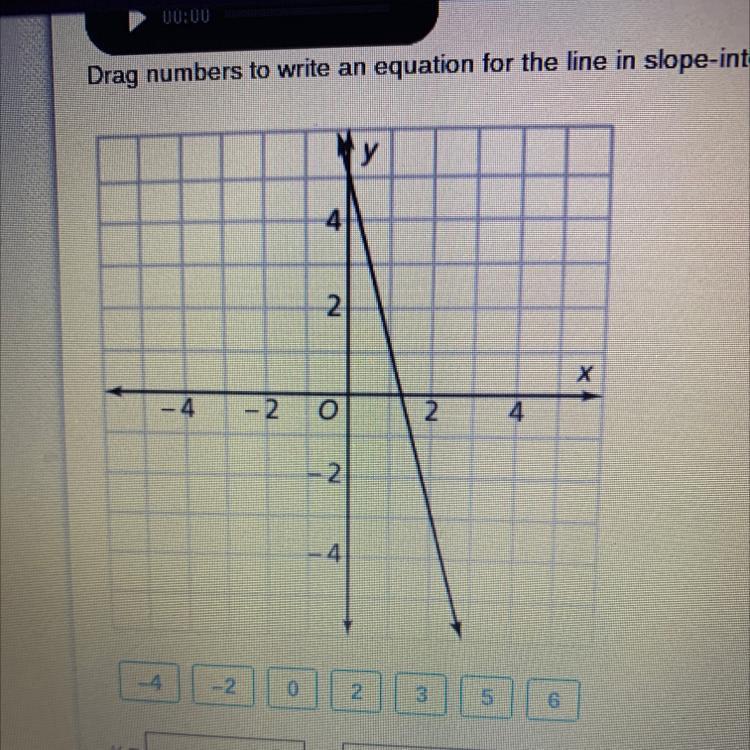
Drag numbers to write an equation for the line slope-intercept form. Numbers may be used once, more than once, or not at all.
Answers
Answer:
y = -3x + 5
Step-by-step explanation:
Find the graph attached
The standard form of calculating the equation of a line is expressed as;
y = mx+c
m is the slope
c is the intercept
Using the coordinate points (0, 5) and (1, 2)
m = 2-5/1-0
m = -3/1
m = -3
Get the intercept
Substitute m = -3 and (0,5) into y = mx+c
5 = -3(0) + c
5 = c
c = 5
Get the required equation
Recall that y = mx+c
Substitute the gotten values
y = -3x + 5
Which symbol would make the statement TRUE?
-3/4
-0.75
A. <
B. >
C. =
D. none of the above

Answers
Answer: C
Step-by-step explanation: -3/4 is equal to -.75 ,
3. Find \( y^{\prime} \) for the following implicit function \( y^{2}-x^{2} y=-2 \)
Answers
The derivative \(\( y' \)\) of the implicit function \(\( y^2 - xy = -2 \)\) is 0, indicating a constant slope with no change in relation to \(\( x \)\).
To find \(\( y' \)\)for the implicit function \(\( y^2 - xy = -2 \)\), we can differentiate both sides of the equation with respect to \(\( x \)\) using the chain rule. Let's go step by step:
Differentiating \(\( y^2 \)\) with respect to \(\( x \)\) using the chain rule:
\(\[\frac{d}{dx}(y^2) = 2y \cdot \frac{dy}{dx}\]\)
Differentiating \(\( xy \)\) with respect to \(\( x \)\) using the product rule:
\(\[\frac{d}{dx}(xy) = x \cdot \frac{dy}{dx} + y \cdot \frac{dx}{dx} = x \cdot \frac{dy}{dx} + y\]\)
Differentiating the constant term (-2) with respect to \(\( x \)\) gives us zero since it's a constant.
So, the differentiation of the entire equation is:
\(\[2y \cdot \frac{dy}{dx} - (x \cdot \frac{dy}{dx} + y) = 0\]\)
Now, let's rearrange the terms:
\(\[(2y - y) \cdot \frac{dy}{dx} - x \cdot \frac{dy}{dx} = 0\]\)
Simplifying further:
\(\[y \cdot \frac{dy}{dx}\) \(- x \cdot \frac{dy}{dx} = 0\]\)
Factoring out:
\(\[(\frac{dy}{dx})(y - x) = 0 \]\)
Finally, solving:
\(\[\frac{dy}{dx} = \frac{0}{y - x} = 0\]\)
Therefore, the derivative \(\( y' \)\) of the given implicit function is 0.
Learn more about derivative
brainly.com/question/29144258
#SPJ11
I need help with this problems please I need a huge explanation

Answers
In this case we must apply the properties of supplementary angles and opposite angles.
1 .
opposite angles
∠ 1 = 120 °
supplementary angles
∠ 1 + ∠ 2 = 180
120 + ∠ 2 = 180
∠ 2 = 180 - 120
∠ 2 = 60 °
The same properties can be applied in the other exercises to solve them.
The solution is:
∠ 1 = 120 °
∠ 2 = 60 °
What is this supposed to mean!?!?!?!?

Answers
Answer:
h = V/B
Step-by-step explanation:
\(\sf V \div B = h\\Reverse\\h = V \div B\)
Answer:
D. h = V/B
Step-by-step explanation:
"Solve...for h" means get h all by itself on one side of the equation.
V = Bh
Divide both sides by B.
V/B = h
Turn it around and you can see the answer in the choices. D. h = V/B is the correct answer.
k = at + w
Solve for T
Please helpp
Answers
Answer:
(k-w)/a = t
Step-by-step explanation:
k = at + w
Subtract w from each side
k-w = at + w-w
k-w = at
Divide each side by a
(k-w)/a = at/a
(k-w)/a = t
Find the percent change and classify as an increase or decrease:
Before: 75
After: 60
Answers
I hope it help you

write 34 as a product of its prime factors. PLEASE HELP I NEED TO TURN IT IN IN % MINUTES
Answers
Answer: Down below
Step-by-step explanation: First of all, as 34 is an even number, so it must be divisible by smallest prime 2.
Thus, 2 must be a factor of 34.
Now, look for number obtained on dividing 34 by 2 i.e.
34÷2=17.
So, 17 is our new number.
Now, look for factors/divisors of 17, which are precisely 1 and 17 i.e. 17 is itself a prime.
This implies only factors possible for 34 are 2 and 17.
Thus ,34 can be written as product of prime numbers 2 and 17 as 34=2×17.
Key idea. Given any number, divide it by smallest divisible prime and look for the number obtained on division.
Now, repeat the process for the number obtained.
If no division by a smaller prime than that number is possible, then our number is itself a prime.
Answer:
2(17)
Step-by-step explanation:
Find the Nth Term: 2, -6, -14, -22.
Thanks.
Answers
Answer:
\(a_{n}\) = - 8n + 10
Step-by-step explanation:
there is a common difference between consecutive terms , that is
- 6 - 2 = - 14 - (- 6) = - 22 - (- 14) = - 8
this indicates the sequence is arithmetic with nth term
\(a_{n}\) = a₁ + (n - 1)d
where a₁ is the first term and d the common difference
here a₁ = 2 and d = - 8 , then
\(a_{n}\) = 2 - 8(n - 1) = 2 - 8n + 8 = - 8n + 10
Sean throws the discus at a school meet and the height of the discus is given by the function h=-16+2 + 38t + 5, where h is in feet and t represents the seconds after throwing. A. What is the initial height of the discus? b. After how many seconds does it take for the discus hit the ground?
Answers
Hence, in response to the provided question, we can say that As a result, function the discus takes approximately 0.03125 seconds to strike the ground.
what is function?Mathematicians research numbers and their variants, equation and related structures, objects and their locations, and prospective locations for these things. The term "module" is used to describe the connection that exists in between set of inputs, each of which has a corresponding output. A function is an input-output connection in which each inputs results in something like a single, distinct return. A domain, codomain, or scope is assigned to each function. Functions are usually denoted by the letter f. (x). An x is used for entry. On capabilities, one-to-one capabilities, multiple prowess, in capabilities, and on capabilities are the four major types of accessible functions.
The supplied function for discus height is as follows:
\(h(t) = -16t^2 + 38t + 5\\h(0) = -16(0)^2 + 38(0) + 5 = 5\)
As a result, the discus's starting height is 5 feet.
\(-16t^2 + 38t + 5 = 0\\\)
To find t, we can apply the quadratic formula:
t = (-b \sqrt(b2 - 4ac)) (2a)
where a=-16, b=38, and c=5.
\(t = (-38 + \sqrt(38^2 - 4(-16)(5))) / (2(-16))\\t = (-38 + \sqrt(1524)) / (-32) (-32)\\t = (-38 + 39) / (-32) (-32)\\\)
As a result, \(t = (-38 + 39) / (32) or t = (-38 - 39) / (32) (-32)\)
t = 1/32 or t = 77/32
As the negative value doesn't make sense in this situation, we chose the positive value:
t = 1/32
As a result, the discus takes approximately 0.03125 seconds to strike the ground.
To know more about function visit:
https://brainly.com/question/28193995
#SPJ1
For each problem: a. Verify that E is a Lyapunov function for (S). Find the equilibrium points of (S), and classify each as an attractor, repeller, or neither. dx dt dy dt = = 2y - x - 3 4 - 2x - y E(x, y) = x² - 2x + y² - 4y
Answers
The Lyapunov function E(x, y) = x² - 2x + y² - 4y is positive definite.
The equilibrium point of the system (S) is (x, y) = (1, 2).
The equilibrium point (1, 2) is classified as a repeller.
To verify whether E(x, y) = x² - 2x + y² - 4y is a Lyapunov function for the system (S), we need to check two conditions:
1. E(x, y) is positive definite:
- E(x, y) is a quadratic function with positive leading coefficients for both x² and y² terms.
- The discriminant of E(x, y), given by Δ = (-2)² - 4(1)(-4) = 4 + 16 = 20, is positive.
- Therefore, E(x, y) is positive definite for all (x, y) in its domain.
2. The derivative of E(x, y) along the trajectories of the system (S) is negative definite or negative semi-definite:
- Taking the derivative of E(x, y) with respect to t, we get:
dE/dt = (∂E/∂x)dx/dt + (∂E/∂y)dy/dt
= (2x - 2)(2y - x - 3) + (2y - 4)(4 - 2x - y)
= 2x² - 4x - 4y + 4xy - 6x + 6 - 8x + 4y - 2xy - 4y + 8
= 2x² - 12x - 2xy + 4xy - 10x + 14
= 2x² - 22x + 14 - 2xy
- Simplifying further, we have:
dE/dt = 2x(x - 11) - 2xy + 14
Now, let's find the equilibrium points of the system (S) by setting dx/dt and dy/dt equal to zero:
2y - x - 3 = 0 ...(1)
-2x - y + 4 = 0 ...(2)
From equation (1), we can express x in terms of y:
x = 2y - 3
Substituting this value into equation (2):
-2(2y - 3) - y + 4 = 0
-4y + 6 - y + 4 = 0
-5y + 10 = 0
-5y = -10
y = 2
Substituting y = 2 into equation (1):
2(2) - x - 3 = 0
4 - x - 3 = 0
-x = -1
x = 1
Therefore, the equilibrium point of the system (S) is (x, y) = (1, 2).
Now, let's classify this equilibrium point as an attractor, repeller, or neither. To do so, we need to evaluate the derivative of the system (S) at the equilibrium point (1, 2):
Substituting x = 1 and y = 2 into dE/dt:
dE/dt = 2(1)(1 - 11) - 2(1)(2) + 14
= -20 - 4 + 14
= -10
Since the derivative is negative (-10), the equilibrium point (1, 2) is classified as a repeller.
In summary:
- The Lyapunov function E(x, y) = x² - 2x + y² - 4y is positive definite.
- The equilibrium point of the system (S) is (x, y) = (1, 2).
- The equilibrium point (1, 2) is classified as a repeller.
Learn more about Lyapunov function
https://brainly.com/question/32668960
#SPJ11
when the population standard deviation is unknown and the sample size is less than 30, what table value should be used in computing a confidence interval for the mean?
Answers
When the population standard deviation is unknown and the sample size is less than 30, we need to use the t-distribution to compute a confidence interval for the mean, and we should consult a t-table to find the appropriate t-value based on the degrees of freedom and the desired level of confidence.
When the population standard deviation is unknown and the sample size is less than 30, we need to use the t-distribution to compute a confidence interval for the mean.
The t-distribution is similar to the standard normal distribution, but with heavier tails, and it is used when the population standard deviation is unknown.
To compute the confidence interval for the mean using the t-distribution, we need to find the appropriate t-value from a t-table. The t-table provides critical values for different degrees of freedom and levels of confidence.
The degrees of freedom for a t-distribution with a sample size of n is (n-1). For example, if we have a sample size of 20, the degrees of freedom would be 19.
To find the appropriate t-value from the t-table, we need to know the degrees of freedom and the desired level of confidence. For example, if we have a sample size of 20 and want to calculate a 95% confidence interval, we would look for the t-value with 19 degrees of freedom and 0.025 (0.05/2) in the middle of the table. This t-value would be used in the formula to calculate the confidence interval for the mean.
Learn more about “ population standard deviation “ visit here;
https://brainly.com/question/13336998
#SPJ4
Apples from a grower’s crop in 2006 were normally distributed with mean 173 grams and standard deviation of 34 grams. Apples weighing less than 130 grams were too small to sell.
Find the proportion of apples from this crop which were too small to sell.
Find the probability that in a picker’s basket of 100 apples, up to 10 apples were too small to sell .
Answers
P(X ≤ 10) represents the probability that up to 10 apples in a basket of 100 are too small to sell.
To find the proportion of apples from the 2006 crop that were too small to sell, we need to calculate the probability that an apple weighs less than 130 grams. We can do this by using the standard normal distribution.
Proportion of apples too small to sell:
Let X be the weight of an apple from the crop. We are given that X follows a normal distribution with a mean of 173 grams and a standard deviation of 34 grams.
To find the proportion of apples weighing less than 130 grams, we need to calculate the cumulative distribution function (CDF) of the standard normal distribution up to the z-score corresponding to 130 grams.
First, we need to standardize the value of 130 grams using the formula:
z = (X - μ) / σ
where X is the value (130 grams), μ is the mean (173 grams), and σ is the standard deviation (34 grams).
z = (130 - 173) / 34 = -43 / 34 ≈ -1.2647
Using a standard normal distribution table or a calculator, we can find the CDF corresponding to this z-score. The CDF represents the proportion of values less than -1.2647 in the standard normal distribution.
Let P(Z < -1.2647) = p
The proportion of apples from the 2006 crop that were too small to sell is approximately p.
Probability of up to 10 apples too small to sell in a basket of 100 apples:
We can use the binomial distribution to calculate the probability of up to 10 apples being too small to sell in a basket of 100 apples.
Let X be the number of apples too small to sell in a basket of 100. The probability of a single apple being too small is p, as calculated in the previous step.
Using the binomial distribution formula, we can calculate the probability of X being less than or equal to 10:
P(X ≤ 10) = Σ (n choose x) * p^x * (1 - p)^(n - x)
where n is the number of trials (100), x is the number of successes (up to 10), and p is the probability of success (as calculated earlier).
This involves summing the probabilities for x = 0, 1, 2, ..., 10.
By calculating this probability, we can determine the likelihood of encountering up to 10 undersized apples in a picker's basket of 100 apples.
Learn more about probability at: brainly.com/question/32117953
#SPJ11
CCC Company ha nine million hare of common tock outtanding and 150,000 7. 5 percent emi-annual bond outtanding. The firm’ common tock i currently elling at a price of 37 dollar per hare. CCC ha an equity beta of 1. 25. A for debt, the firm’ outtanding bond are quoted at 95 percent of par value and have 16 year to maturity. The par value on each bond i 1,000 dollar. Market rik premium i 8 percent. T-bill are offering a yield of four percent.
Answers
Company ha nine million hare of common tock outtanding and 150,000 7. 5 percent emi-annual bond outtanding then value is 0.7466
Equity is the amount of money that a company's proprietor has put into it or owns. On a enterprise's balance sheet, the distinction between its liabilities and assets suggests how a great deal fairness the corporation has. the proportion charge or a price set via valuation professionals or investors is used to discern out the equity fee.
Book value weight
Particulars amount [millions ] (amount/total)
common stock $150000 0.2534
first issue $1.2500 0.4072
second issue $75.00 0.3394
Total Book value $221.00
Weight of equity on book value basis = 0.2534
Weight of debt on book value basis = 0.7466
learn more about of debt here
https://brainly.com/question/29568305
#SPJ4
Compute the expected rate of return for the following two-stock portfolio Stock Expected Return Standard Deviation Weight A 18% 40% 0.70 B 12% 28% 0.3
Answers
The expected rate of return for the portfolio is calculated as follows:
(18% * 0.70) + (12% * 0.30) = 12.6% + 3.6% = 16.2%.
To compute the expected rate of return for a portfolio, we need to consider the expected return and weight of each stock in the portfolio. The expected return represents the anticipated return for each stock, while the weight represents the proportion of the portfolio's total value allocated to each stock.
In this case, Stock A has an expected return of 18% and a weight of 0.70, meaning it accounts for 70% of the portfolio's total value. Stock B, on the other hand, has an expected return of 12% and a weight of 0.30, accounting for 30% of the portfolio's total value.
To calculate the expected rate of return for the portfolio, we multiply the expected return of each stock by its respective weight. For Stock A, the calculation is 18% * 0.70 = 12.6%, and for Stock B, it is 12% * 0.30 = 3.6%.
Finally, we sum up the results of these calculations: 12.6% + 3.6% = 16.2%. Therefore, the expected rate of return for the two-stock portfolio is 16.2%.
To learn more about proportion click here, brainly.com/question/31548894
#SPJ11
2.5 tablespoon liquid product to gallon of water - how much liquid product should be reduced if using 2 cups water ?
Answers
To determine how much liquid product should be reduced when using 2 cups of water, we need to find the ratio between tablespoons and cups. When using 2 cups of water, approximately 0.31 tablespoons of liquid product should be used.
Given that 2.5 tablespoons of the liquid product are used for a gallon of water, we can set up a proportion to find the amount needed for 2 cups of water.
⇒The ratio can be expressed as:
2.5 tablespoons / 1 gallon = x tablespoons / 2 cups
⇒To solve for x, we can cross-multiply and solve for x:
2.5 tablespoons * 2 cups = x tablespoons * 1 gallon
⇒This simplifies to:
5 tablespoons = x tablespoons * 1 gallon
⇒Since we want to find the amount for 2 cups, we can convert the 1 gallon into cups, which is equal to 16 cups.
5 tablespoons = x tablespoons * 16 cups
⇒Next, we can solve for x by dividing both sides of the equation by 16:
5 tablespoons / 16 = x tablespoons
⇒x ≈ 0.31 tablespoons
Therefore, when using 2 cups of water, approximately 0.31 tablespoons of liquid product should be used.
Learn more about the liquid product here:
https://brainly.com/question/14508772
#SPJ11
Can someone answer q3

Answers
Step-by-step explanation:
\( \frac{2x + 5}{4} = 9x - 11\)
2x + 5 = 4(9x - 11)
2x + 5 = 36x - 44
36x - 44 = 2x + 5
36x - 2x = 5 + 44
34x = 49
x = 49/34
Answer:
x=49/34
Step-by-step explanation:
1.) Multiply both sides by 4
(4) 2x+5/4 = 9x-11 (4)
2x+5 = 36x-44
2.) Subtract 2x from both sides
2x+5 = 36x-44
-2 -2
5 = 34x-44
3.) Add 44 to both sides
5 = 34x-44
+44 +44
49=34x
4.) Divide by 34
49/34 = 34x/34
x=49/34
1011+1111=in binary answer, anyone that answer me first I will follow u
Answers
Answer:
Step-by-step explanation:
answer is \((11010)_{2}\)

a=3p+1
Solve for p
please help me solve this
Answers
Answer:
Step-by-step explanation:
p= a/3 - 1/3
42. Find the equation of the sphere with center C(−2,3,7) that is tangent to the plane 2x+3y−6z=5.
Answers
To find the equation of the sphere tangent to the plane 2x + 3y - 6z = 5 with center C(-2, 3, 7), we need to find the radius of the sphere. The equation of the sphere is (x + 2)^2 + (y - 3)^2 + (z - 7)^2 = 36.
The distance from the center of the sphere to the plane is equal to the radius. We can use the formula for the distance between a point (x, y, z) and a plane Ax + By + Cz + D = 0:
Distance = |Ax + By + Cz + D| / sqrt(A^2 + B^2 + C^2)
In this case, the plane equation is 2x + 3y - 6z - 5 = 0. Plugging in the coordinates of the center C(-2, 3, 7) into the formula, we have:
Distance = |2(-2) + 3(3) - 6(7) - 5| / sqrt(2^2 + 3^2 + (-6)^2)
= |-4 + 9 - 42 - 5| / sqrt(4 + 9 + 36)
= |-42| / sqrt(49)
= 42 / 7
= 6
So, the radius of the sphere is 6.
The equation of a sphere with center C(-2, 3, 7) and radius 6 is:
(x + 2)^2 + (y - 3)^2 + (z - 7)^2 = 6^2
Simplifying further, we have:
(x + 2)^2 + (y - 3)^2 + (z - 7)^2 = 36
Therefore, the equation of the sphere is (x + 2)^2 + (y - 3)^2 + (z - 7)^2 = 36.
Learn more about radius here
https://brainly.com/question/24375372
#SPJ11
What value could you write in after 3x that would make the equation true for all values of x?
3x+12 = 3x+

Answers
Answer:
12
Step-by-step explanation:
Answer:
12
Step-by-step explanation:
Identity property/ Associative Property
Would the point (2,7) be on the line y = 2x +7
Answers
No
Step-by-step explanation:A point is on a line if that point satisfies the equation.
Testing Points
To test if the point (2,7) is on the line y = 2x + 7, we need to plug the point into the equation. For the coordinate pair (2,7), the x-value is 2 and the y-value is 7. So, plug 2 in for x and 7 in for y.
7 = 2(2) + 7Then, simplify.
7 = 11As you can see, 7 does not equal 11. Thus, point (2,7) cannot be a point on the given line.
Other Points
We can do this same test with other points such as (1,9). The x-value is 1 and the y-value is 9, so now we can plug them in.
9 = 2(1) + 79 = 9Since 9 equals 9 is a true statement, the point (1,9) is a point on the given line.
Write two equations-one in logarithmic form and one in exponential form-that represent the
statement: "the natural logarithm of 10 is y".
Answers
Expressions can be expressed in logarithmic forms, and in exponential forms
The two equations are \(\ln(10) = y\) and \(10 = e^y\)
How to determine the expressions.The statement is given as "the natural logarithm of 10 is y".
The logarithmic expression of the above statement is:
\(\ln(10) = y\)
Rewrite the above expression, as an exponential equation
\(10 = e^y\)
Hence, the two equations are \(\ln(10) = y\) and \(10 = e^y\)
Read more about logarithms at:
https://brainly.com/question/1832186
im struggling with this :D i need help!

Answers
Answer:
not a real number
Step-by-step explanation:
any negative number under a square root sign, except for 0, isn't real
On evaluating the given roots,
(a) \($-(\sqrt[3]{8}) = -2$\)
(b) \($\sqrt[4]{-81}$\) is not a real number
(a) \($-(\sqrt[3]{8})$\):
The cube root of 8 is the number that, when raised to the power of 3, equals 8. In this case, the cube root of 8 is 2, because \(2^3 = 8\).
Since we have a negative sign in front of the cube root, the result will be the negative value of the cube root of 8.
Therefore, \($-(\sqrt[3]{8}) = -2$\).
(b) \($\sqrt[4]{-81}$\):
The fourth root of a number is the number that, when raised to the power of 4, equals the given number.
In this case, we are looking for the fourth root of -81.
However, the fourth root of a negative number is not a real number. This is because raising a positive number to an even power (in this case, 4) will always result in a positive value, and there is no real number that, when raised to the power of 4, gives a negative result.
Therefore, the fourth root of -81 is not a real number.
To know more about roots, refer here:
https://brainly.com/question/12105008
#SPJ2
(a) Find a nonzero vector orthogonal to the plane through the points P, Q, and R, and (b) find the area of triangle PQR.P(1, 0, 1), Q(-2, 1, 3), R(4, 2, 5)
Answers
The vector orthogonal to the plane through the points P, Q, and R is (8, -8, 12), and the area of triangle PQR is \($\sqrt{301}$\).
For part (a), we can find a nonzero vector orthogonal to the plane through the points P, Q, and R by constructing a normal vector to the plane using the cross product of two vectors in the plane. The two vectors in the plane are \($\vec{PQ} = (1- (-2), 0-1, 1-3) = (3, -1, -2)$\) and \($\vec{PR} = (1-4, 0-2, 1-5) = (-3, -2, -4)$\). Taking the cross product of the two vectors gives us the normal vector to the plane, \($\vec{n} = \vec{PQ} \times \vec{PR} = (8, -8, 12)$\). Therefore, the vector orthogonal to the plane is \($\vec{n} = (8, -8, 12)$.\)
For part (b), the area of triangle PQR can be found using the formula for Heron's Formula, which states that the area of a triangle with sides a, b,and c is given by
\($A = \sqrt{s(s-a)(s-b)(s-c)}$\)
where \($s = \frac{a+b+c}{2}$\) . In this case, the sides are \($a = \|\vec{PQ}\| = \sqrt{3^2 + (-1)^2 + (-2)^2} = \sqrt{14}$, $b = \|\vec{QR}\| = \sqrt{(-2-4)^2 + (1-2)^2 + (3-5)^2} = \sqrt{14}$\), and\($c = \|\vec{PR}\| = \sqrt{(-3)^2 + (-2)^2 + (-4)^2} = \sqrt{29}$\). Plugging these values into the formula, we get
\(= \sqrt{s(s-a)(s-b)(s-c)} = \sqrt{\frac{7(7-\sqrt{14})(7-\sqrt{14})(7-\sqrt{29})}{4}} = \sqrt{7(7-\sqrt{14})^2(7-\sqrt{29})} = \sqrt{7(7-\sqrt{14})^2(\sqrt{14}+\sqrt{29})} = \sqrt{7(7-\sqrt{14})^2\sqrt{43}} = \sqrt{301}$\)Therefore, the area of triangle PQR is \($\sqrt{301}$\)
The vector orthogonal to the plane through the points P, Q, and R is (8, -8, 12), and the area of triangle PQR is \($\sqrt{301}$\).
Learn more about area of triangle here:
https://brainly.com/question/19305981
#SPJ4
Which equation represents a linear function?

Answers
Answer: Equation 3
Step-by-step explanation:
It does not have any exponents, meaning it's linear
Answer:
equation 3
Step-by-step explanation:
no exponents
The distributor for Hits on a Shoestring has changed her mind
about rap. She now believes that rap is more popular in her
territory than rock. She tells the company that it can make up to
twice as many rap CDs as rock CDs.
The remaining facts are the same as in Rock 'n' Rap. Here is a
summary of the constraints.
NO
Producing a rock CD costs an average of $15,000. Producing a
rap CD costs about $12,000.
Producing a rock CD takes about 18 hours. Producing a rap CD
takes about 25 hours.
Hits on a Shoestring must use at least 175 hours of production
time. Hits on a Shoestring can spend up to $150,000 on
production next month.
Each rock CD makes a profit of $20,000. Each rap CD makes a
profit of $30,000.
Find how many CDs of each type Hits on a Shoestring should
make next month to maximize its profits. Justify your reasoning.
Remember, the company can plan to make a fraction of a CD
next month and finish it the month after.
I
Answers
It should produce 23 rock CDs and 46 rap CDs next month to maximize its profits.
What is the optimal number of CDs to maximize profits?Assume number of rock CDs produced is R
Assume number of rap CDs produced is P.
The distributor said that up to twice as many rap CDs can be produced as rock CDs, so we have constraint\(P \leq 2R.\)
We also have the following constraints:
Production time constraint: 18R + 25P ≥ 175 (to use at least 175 hours of production time).Production cost constraint: 15,000R + 12,000P ≤ 150,000 (to spend up to $150,000 on production).To maximize profits, we need to maximize the objective function:
Profit = 20,000R + 30,000P
The optimization problem. Let us e\rearrange the production time constraint to obtain P in terms of R:
25P ≥ 175 - 18R
P ≥ (175 - 18R)/25
Substitute the inequality into production cost constraint:
15,000R + 12,000[(175 - 18R)/25] ≤ 150,000
Simplifying the inequality, we get:
375R - 216R ≤ 3750
159R ≤ 3750
R ≤ 3750/159
R ≤ 23.59
Substitute R = 23 into the inequality P ≤ 2R, we get:
P ≤ 2(23)
P ≤ 46.
Read more about revenue function
brainly.com/question/19755858
#SPJ1
Solve these two questions for 50 pts.

Answers
Answer:
RS = 26x = 6Step-by-step explanation:
Question 1V and W are midpoints of RU and ST ⇒ VW is a midsegment
VW = 1/2(RS + UT) ⇒ RS = 2*VW - UT
Substitute values:
2x + 15 = 2(2x + 5) - (6x - 37)2x + 15 = 4x + 10 - 6x + 372x + 15 = -2x + 472x + 2x = 37 - 154x = 22x = 5.5RS = 2x + 15 = 2(5.5) + 15 = 11 + 15 = 26
Question 2
Trapezoid given with congruent sides, JM = KLAngle J and K are congruent, both are (7x + 2)Angles M and L are congruent, both are (2x - 14)J and M are supplementary, so sum to 180°
7x + 2 + 25x - 14 = 18032x = 192x = 192/32x = 6Answer:
RS = 26
x = 6
Step-by-step explanation:
The cost of a loan for $600 over 2 years is $120.00. What was the rate on the loan?
Answers
Answer:
your annual interest rate will be 5%.
Step-by-step explanation:
brainliest please?
It was 120 dollars over the span of 2 years, so we divide 120 by 2.
120/2=60
So the loan costed $60 per year
---
hope it helps
A pizza is divided into 18 equal pieces. Some teachers and students share the pizza. Each teacher eats 4 pieces, and each student eats 2
pieces of pizza. They eat all of the pizza.
How many teachers are there, and how many students are there?
PLS HELPP

Answers
Answer:
C
Step-by-step explanation:
Each teacher eats 4 pieces
Each student eats 2 pieces
They eat all 18 pieces
Look at answer choice C
4*3+3*2 = 18