Let csc(x) = five-thirds, where 0° < x < 90°. which expression has a value of three-fourths?
a. sec(x)
b. cos(x)
c. cot(x)
d. tan(x)
Answers
The expression which ehi has a value of three-fourths is cos(x).
What is expression in math?Expression in math is an equation, statement, or a combination of symbols and numbers that represent a mathematical operation or value. It is used to calculate or solve mathematical problems. Expressions can be simple or complex, and may involve constants, variables, operations, and functions.
This can be determined by rearranging the equation csc(x) = five-thirds.
This gives us cos(x) = three-fourths.
Therefore, the expression with a value of three-fourths is cos(x).
To know more about expression click-
https://brainly.com/question/1859113
#SPJ4
Related Questions
approximately how fast is a person located at the earth's equator traveling due to the rotation of the earth? hint: a person located at the equator will go once along the circumference of a circle with radius equal to the radius of the earth in a time interval equal to 24 hours. speed is equal to distance traveled divided by the time interval.
Answers
The speed of the person located at earth's equator traveling due to rotation is, 1670 km/hr.
The person at equator traveling due to it's rotation will cover one complete round of earth in 24 hours. Hence the distance travelled is the circumference of the earth.
The radius of the earth is, 6 378.1 kilometers.
The circumference can be calculated as, 2×π×R
Using R = 6 378.1 kilometers,
Circumference = 2×π×6 378.1 kilometers
Circumference = 40090.91 kilometers.
The distance traveled = 40090.91 kilometers.
Time taken is 24 hrs.
Hence speed = distance/time
Speed = 40090.91/24
Speed = 1670 km/hr
The speed of the person is 1670 km/hr.
To know more about the speed, here
brainly.com/question/29775794
#SPJ4
Which is the best definition of a conic section ? cone and plane cone and line cone and point cone and circle
Answers
The correct option is cone and plane. A conic section is the intersection of a plane and a cone. The best definition of a conic section is "cone and plane".
The definition of conic section is a conic section is a shape that is formed when a right circular cone intersects a plane. Depending on the angle of the plane concerning the center line of the cone, the conic sections are classified into four types. They are a circle, parabola, ellipse, and hyperbola. Each type of conic section has a unique shape and properties.
Learn more about cone
https://brainly.com/question/10670510
#SPJ11
Write an absolute value expression you could use to find the absolute value of 3.1 + (-6.3)
Answers
The absolute value of a number expression 3.1 + (-6.3) is 3.2 the answer is 3.2.
What is an arithmetic operation?It is defined as the operation in which we do the addition of numbers, subtraction, multiplication, and division. It has a basic four operators that is +, -, ×, and ÷.
It is given that:
The number expression is:
= 3.1 + (-6.3)
To find the absolute value of 3.1 + (-6.3):
= |3.1 + (-6.3)|
= |3.1 - 6.3|
= |-3.2|
= 3.2
Thus, the absolute value of a number expression 3.1 + (-6.3) is 3.2 the answer is 3.2.
Learn more about the arithmetic operation here:
brainly.com/question/20595275
#SPJ4
Answer two questions about Equations AAA and BBB: \begin{aligned} A.&&\dfrac x4+1&=-3 \\\\ B.&&x+4&=-12 \end{aligned} A. B. 4 x +1 x+4 =−3 =−12 1) How can we get Equation BBB from Equation AAA? Choose 1 answer: Choose 1 answer: (Choice A) A Rewrite one side (or both) using the distributive property (Choice B) B Rewrite one side (or both) by combining like terms (Choice C) C Multiply/divide only one side by a non-zero constant (Choice D) D Multiply/divide both sides by the same non-zero constant 2) Based on the previous answer, are the equations equivalent? In other words, do they have the same solution? Choose 1 answer: Choose 1 answer: (Choice A) A Yes (Choice B) B No
Answers
The given equations are as follows
\(\begin{aligned} A.&&\dfrac x4+1&=-3 \\\\ B.&&x+4&=-12 \end{aligned}\)
(1) First, multiply both sides of equation A by 4, we have
\(4\times\left(\frac{x}{4} +1\right)=4\times(-3)\)
Then, rewrite the left-hand side of the above equation by using the distributive property, we have
\(4\times\frac{x}{4}+4\times1=4(-3)\)
\(\Rightarrow x+4=-12\)
This is the required equation B.
In this way, first use choice D: Multiply both sides by the same non-zero constant, i.e 4.
Then, apply choice A to solve the equation, i.e using the distributive property to solve the left-hand side of the equation.
(2) In the previous answer, equation B has been derived from equation A, hence, both the equations are equivalent.
As both the equations are the same, so both will have the same solution.
Yes, they have the same solution.
Which of the following is correct for determining the length of x to the nearest tenth of a metre?
cos 42 = x/6
tan 48 = x/5
sin 48 = x/5
tan 42 =x/6

Answers
I NEED HELPP‼️‼️‼️‼️ASAPPPAND ALSO EXPLAIN
find the value of p
1) p=7
2) p=20
3) p= 145
4) p=75

Answers
Answer:
p= 20
Step-by-step explanation:
360 - 145 -75 = 7p
140 =7p
140 ÷7 =7p ÷7
20 = p
Answer:
p= 20°
Step-by-step explanation:
here's your solution
==> Angle formed around a point = 360°
==> 145° + 75° + 7p° = 360°
==> 220° + 7p° = 360°
==> 7p° = 360° - 220°
==> 7p° = 140°
==> p = 140°/7
==> p= 20°
\(hope \: it \: helps\)
Look at pictures help please 11 points

Answers
Answer:
negative 70 (-70)
Step-by-step explanation:
below sea level, so below zero, would be -70
Answer:
-70
Step-by-step explanation:
Its below it would be in the negatives
given that (-2,-2) is on the graph of f(x), find the corrisponding point for the function f(x)+5
Answers
Answer:
(-2, 3)
Step-by-step explanation:
The +5 represents shifting 5 units up, so we can add 5 to the y coordinate.
This gives us (-2, -2+5)=(-2, 3)
9) The diameter of a circular ice skating rink is 32 feet. What is the approximate area of the ice skating rink? Use a = 3.14. a) 803.84 square feet b) 50.24 square feet c) 100.48 square feet d) 64 square feet
Answers
Answer:
a) 803.84 square feet
Step-by-step explanation:
\(\sf{area~of~circle~=~\pi r^{2} }\\\sf{radius~ =~half~of~diameter}\)
so 32 / 2 = 16 = radius
\(\sf{radius^{2} = 16^{2}=256}\)
256 x 3.14 (because we are taking π as 3.14)
= 803.84
Hope this helps! If you need any further explanation, let me know!
- profparis
a baker wants to study the average weight of her 100 loaves of bread. she weighs a random selection of 10 loaves and records their weight in grams: 790,680,900,855,745,740,874,903,876,800. what is the sample mean of the weight of the loaves in the bakery? round your answer to the nearest tenth. do not include units in your answer.
Answers
The sample mean of the weight of the loaves in the bakery is 797.3 grams.
Given data:Number of loaves of bread = 10Weights of loaves in grams = {790, 680, 900, 855, 745, 740, 874, 903, 876, 800}
Mean or average weight of the loaves in the bakery can be calculated using the formula;
Mean = (Sum of weights of all loaves) / Number of loavesTherefore,Mean = (790 + 680 + 900 + 855 + 745 + 740 + 874 + 903 + 876 + 800) / 10 = 797.3
So, the sample mean of the weight of the loaves in the bakery is 797.3 grams.
To know more about Mean refer to-
brainly.com/question/30112112#
#SPJ11
19 percent of the employees at a large biotech firm are working from home. [you may find it useful to reference the z table.] a. in a sample of 40 employees, what is the probability that more than 18% of them are working from home?
Answers
The probability of more than 18% of a sample of 40 employees at a large biotech firm working from home is 0.2628 or 26.28%.
To calculate the probability, we can use the normal distribution and the z-score formula: z =\((x - μ) / (σ / sqrt(n))\) where x is the sample proportion (in decimal form),\(μ\) is the population proportion (in decimal form), \(σ\) is the population standard deviation (in decimal form), and n is the sample size.
Given that, 19% of the employees at the biotech firm are working from home, we can assume that the population proportion is 0.19. The population standard deviation is not given, so we can use the formula: \(σ = sqrt(p(1-p))\) where p is the population proportion. Plugging in the values, we get: \(σ = sqrt(0.19(1-0.19)) = 0.3929\) Now, we can plug in the values to find the z-score: z = (0.18 - 0.19) / (0.3929 / sqrt(40)) = -0.7606
Using a z-table, we can find the probability that a z-score is less than -0.7606, which is 0.2234. To find the probability that more than 18% of the sample is working from home, we subtract this probability from 1: P(x > 0.18) = 1 - P(x <= 0.18) = 1 - 0.2234 = 0.7766.
Hence, the probability of more than 18% of a sample of 40 employees at the biotech firm working from home is 0.7766 or 77.66%.
Learn more about probability here:
https://brainly.com/question/14210034
#SPJ4
The function, f(n) = 70n – 400, models the profit of the instructor of a guitar class per month, where n is
e number of students enrolled in the class.
How many students must be enrolled in the class for the instructor to make a profit?
ow many students must be enrolled in the class if the instructor needs to make $1,000.00 profit per
onth?
Answers
Using the given function, it is found that:
6 students need to be enrolled for the instructor to make a profit.20 students must be enrolled for the instructor to make a profit of $1,000 a month.What is the profit function?The profit when n students are enrolled in the class is given by:
f(n) = 70n - 400.
A profit is made when f(n) > 0, hence:
70n - 400 > 0
70n > 400
n > 5.71.
6 students need to be enrolled for the instructor to make a profit.
A profit of $1,000 is made when f(n) = 1000, hence:
70n - 400 = 1000
70n = 1400.
n = 20.
20 students must be enrolled for the instructor to make a profit of $1,000 a month.
More can be learned about functions at https://brainly.com/question/25537936
Atleast 6 students must be enrolled to make a profit and 20 student are needed to make $1,000.00 profit per month.
What is an equation?An equation is an expression that shows the relationship between two or more variables and numbers.
Given the function:
f(n) = 70n - 400
To make a profit, f(n) > 0, hence:
70n - 400 > 0
n > 6
For a profit of $1000:
70n - 400 = 1000
n= 20
Atleast 6 students must be enrolled to make a profit and 20 student are needed to make $1,000.00 profit per month.
Find out more on equation at: https://brainly.com/question/2972832
PLSSS HELP THIS IS HARD ANYONE
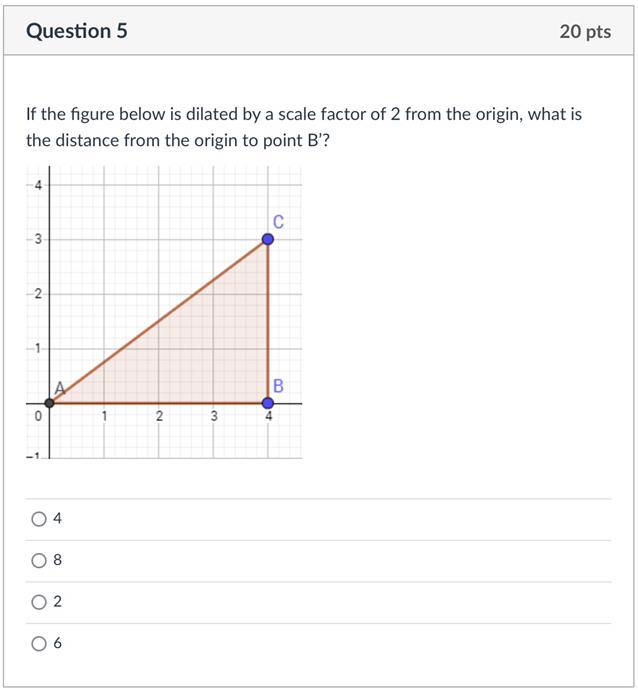
Answers
Answer:
b: 8
Step-by-step explanation:
with dilating by 2, the B' figure would be bigger than B
because 4*2 = 8
I need help on this pls

Answers
Answer:
Area= 56 cm²
Step-by-step explanation:
Figure given is a rhombus
Area= 1/2*d1*d2
On a world , the distance between city A and city B is 5,625 inches. The two cities are actually 1688 miles apart. On the same , what would be the distance between city C and city D, two cities that are actually 1296 miles apart? Use a proportion to solve this problem.
Answers
Answer:
The distance between C and D is 4.2768 inches.
Step-by-step explanation:
As from A to B the distance is 5.625 inches and actual is 1688 miles
so,
1 mile = 5.625/1688 = 0.0033 inches
So, the distance between C and D is 1296 miles
= 1296 x 0.0033 inches = 4.2768 inches
Explain how to get to answer

Answers
Answer:
The length of CD is
"The Right Triangle Altitude Theorem says that the product of AD times DB must equal the length of \(CD^{2}\). Since 4 * 6 = 24, CD must be \(\sqrt{24}\).
\(AC^{2} = AD^{2} + CD^{2}\)
\(AC^{2} = 40\)
\(AC = \sqrt{40} = 2\sqrt{10}\)

c. find the uniform continuous probability for p(25 < x < 45) for u(15, 65). (round your answer to 1 decimal place.)
Answers
The uniform continuous probability for the interval (25 < x < 45) within the uniform distribution U(15, 65) can be found by calculating the proportion of the total range that falls within that interval.
To calculate the probability, we need to determine the length of the interval (45 - 25) and divide it by the length of the entire range (65 - 15).
Length of the interval: 45 - 25 = 20
Length of the entire range: 65 - 15 = 50
Now, we divide the length of the interval by the length of the entire range to obtain the probability:
Probability = (Length of interval) / (Length of entire range) = 20 / 50 = 0.4
Therefore, the uniform continuous probability for p(25 < x < 45) within the uniform distribution U(15, 65) is 0.4, rounded to one decimal place.
To learn more about uniform continuous probability click here brainly.com/question/13257446
#SPJ11
What is the the simplified form of the following expression? 5(t-1)
A t + (-5)
B 6t
C 5t + (-5)
D 5t + (-1)
Answers
5(t-1), we multiply 5 by t first to get 5t
then, multiply 5 by -1 to get -5.
hence, 5(t-1) = 5t-5, which is equal to 5t + (-5).
so your answer is C
many quantitative models of decision theory are based on comparing a single measure of effectiveness, generally some form of utility to the decision maker.a. true b. false
Answers
The statement many quantitative models of decision making are based on comparing a single measure of effectiveness, generally some form of utility to the decision maker is true. So, the correct optio is option a. true.
Many quantitative models of decision theory, such as Expected Utility Theory and also Multi-Attribute Utility Theory, involve comparing a single measure of effectiveness, typically some form of utility, to the decision maker. This allows for the evaluation and comparison of different options based on their expected outcomes and potential risks.
It helps the decision maker determine the best course of action.
Decision theory is a branch of probability. It is concerned with analytic philosophy. It deals with the decision making processes based on probabilities depending on the various factors and the numerical consequences of the outcome.
Therefore, the statement about the decision theory based on comparing a single measure of effectiveness is true.
Know more about decision making here:
https://brainly.com/question/796795
#SPJ11
algebra 2-2
solve \(\sqrt{x}+3=-6\)
√x+3=-6
Answers
The solution of equation is x=-3
What is Algebra?Algebra is the study of abstract symbols, while logic is the manipulation of all those ideas.
The acronym PEMDAS stands for Parenthesis, Exponent, Multiplication, Division, Addition, and Subtraction. This approach is used to answer the problem correctly and completely.
Given
The equation;√x+3=-6
Now,
√x=-6-3
√x=-9
x=-3
Therefore the answer of the given equation will be -3
More about the Algebra link is given below.
brainly.com/question/953809
#SPJ1
(x^2 + 2x + 2)(x + 5) = 0
Answers
Answer:
\( {x}^{2} + 2x + 2 = 0 \: no \: solution \\x + 5 = 0 - \: \: \: \: \: x = - 5 \\ sox = - 5 \)

Pls help question about total pay
Show working out

Answers
\(7\frac{1}{2}\implies 7.5\hspace{5em}1\frac{1}{4}\implies 1.25 \\\\[-0.35em] ~\dotfill\\\\ \stackrel{ \textit{Monday through Friday} }{\stackrel{ days }{(5)}\stackrel{ rate }{(10.80)}\stackrel{ hours }{(7.5)}}~~ + ~~\stackrel{ Saturday }{\stackrel{ days }{(1)}\stackrel{ rate }{(10.80)(1.25)}\stackrel{ hours }{(7.5)}} \\\\\\ 405~~ + ~~101.25\implies \text{\LARGE 506.25}\)
ASAP PLEASE WILL GIVE BRAINLIEST

Answers
The two (2) possible locations of point F include the following: F. [7, 9.5].
How to determine the coordinates of F?In this scenario, line ratio would be used to determine the coordinates of the point on the directed line segment that partitions the segment into a ratio of 5 to 3.
Mathematically, line ratio can be used to determine the coordinates of F and this is modeled by this mathematical expression:
F(x, y) = [(mx₂ + nx₁)/(m + n)], [(my₂ + ny₁)/(m + n)]
Given the following parameters:
Point (x, y)= (4, 11)
Point (x, y) = (8, 9)
m:n = 3:1
Substituting the given parameters into the line ratio formula, we have;
F(x, y) = [(mx₂ + nx₁)/(m + n)], [(my₂ + ny₁)/(m + n)]
F(x, y) = [(3(8) + 1(4))/(3 + 1)], [(3(9) + 1(11))/(3 + 1)]
F(x, y) = [(24 + 4)/(3 + 1)], [(27 + 11)/(3 + 1)]
F(x, y) = [(28)/(4)], [(38)/(4)]
F(x, y) = [7, 9.5]
Read more on line ratio here: brainly.com/question/14457392
#SPJ1
which table can be represented by the equation y=3x+2
Answers
Use elimination to solve eachsystem of equations2x + 3y = 9 8x - 5y = 19
Answers
Multiply the first equation by 4:
\(\begin{gathered} 4(2x+3y=9) \\ 8x+12y=36 \end{gathered}\)Subtract the second equation:
\(\begin{gathered} 8x+12y=36 \\ - \\ 8x-5y=19 \end{gathered}\)This is:
\(\begin{gathered} 8x+12y-(8x-5y)=36-19 \\ 8x+12y-8x+5y=17 \end{gathered}\)Simplify:
\(\begin{gathered} 17y=17 \\ \frac{17y}{17}=\frac{17}{17} \\ y=1 \end{gathered}\)Substitute y = 1 in the first equation:
\(\begin{gathered} 2x+3(1)=9 \\ 2x+3=9 \end{gathered}\)Ans solve for x:
\(\begin{gathered} 2x+3-3=9-3 \\ 2x=6 \\ \frac{2x}{2}=\frac{6}{2} \\ x=3 \end{gathered}\)Answer:
x = 3
y = 1
The proportion of a normal distribution located between z = .50 and z = -.50 is ____.
Answers
The proportion of a normal distribution located between z = .50 and z = -.50 will be 38.2%.
We have,
A normal distribution located between z = 0.50 and z = -0.50,
So,
Now,
From the Z-score table,
We get,
The Probability corresponding to the Z score of -0.50,
i.e.
P(-0.50 < X < 0) = 0.191,
And,
The Probability corresponding to the Z score of -0.50,
i.e.
P(0 < X < 0.50) = 0.191,
Now,
The proportion of a normal distribution,
i.e.
P(Z₁ < X < Z₂) = P(Z₁ < X < 0) + P(0 < X < Z₂)
Now,
Putting values,
i.e.
P(-0.50 < X < 0.50) = P(-0.50 < X < 0) + P(0 < X < 0.50)
Now,
Again putting values,
We get,
P(-0.50 < X < 0.50) = 0.191 + 0.191
On solving we get,
P(-0.50 < X < 0.50) = 0.382
So,
We can write as,
P(-0.50 < X < 0.50) = 38.2%
So,
The proportion of a normal distribution is 38.2%.
Hence we can say that the proportion of a normal distribution located between z = .50 and z = -.50 will be 38.2%.
Learn more about normal distribution here
https://brainly.com/question/13759327
#SPJ4
Find the dimensions of a rectangle with area 1,728 m2 whose perimeter is as small as possible
Answers
The dimensions of a rectangle with area 1728 square meter whose perimeter is as small(minimum) as possible are 41.57m and 41.56m.
Let the dimension of the rectangle be x and y m.
According to the given question.
The area of the rectangle is 1728 square meter.
⇒ x × y = 1728
⇒ x = 1728/y
Since, the perimeter of the rectangle is the sum of the length of its boundary.
Therefore,
Perimeter of the recatngle with dimensions x and y is given by
Perimeter of the rectangle, P = 2(x + y)
⇒ P = 2(1728/y + y)
⇒ P = 3456/y + 2y
Differentiate the above equation with respect to y
⇒ \(P^{'} = -\frac{3456}{y^{2} } + 2\)
For the minimum(small) perimeter equate the above equation to 0.
⇒ \(-\frac{3456}{y^{2} } + 2 = 0\)
⇒ \(2y^{2} =3456\)
⇒ \(y^{2} = \frac{3456}{2}\)
⇒ y^2 = 1728
⇒ y = √1728
⇒ y = 41.56 m
Therefore,
x = 1728/41.56
⇒ x = 41.57 m
Hence, the dimensions of a rectangle with area 1728 square meter whose perimeter is as small(minimum) as possible are 41.57m and 41.56m.
Find out more information about minimum perimeter of the recatngle here:
https://brainly.com/question/2500683
#SPJ4
For the given functions, find (f-g)(x). f(x)=49-x² and g(x)=7-x A. -x²-x-56 B. -x²+x+42 C. 7+x D. x³-7x²-49x=343
Answers
For the given functions, (f - g)(x) = f(x) - g(x) = -x² + x + 42. The correct option is B.
To find (f - g)(x), we need to subtract the function g(x) from f(x).
f(x) = 49 - x²
g(x) = 7 - x
Substituting these values, we have:
(f - g)(x) = f(x) - g(x)
= (49 - x²) - (7 - x)
= 49 - x² - 7 + x
= -x² + x + 42
Therefore, the answer is option B: -x² + x + 42.
To know more about functions, refer to the link below:
https://brainly.com/question/9554035#
#SPJ11
2 A bag contains & blacks balls and 5 yellow balls, 2 balls are taken at random one after the other without replacement find-the probability that they are both black they fare both yellow & the first as yellow - and the second is black one is yellow the other is black they are of the same colour
Answers
The probability values are calculated and listed below
Finding the probabilitiesThey are both black
Here, we have
Black = 3
Yellow = 5
Sice the balls are not replaced, we have
P(Both black) = 3/8 * 2/7
P(Both black) = 3/28
They are both yellow
Sice the balls are not replaced, we have
P(Both Yellow) = 5/8 * 4/7
P(Both Yellow) = 5/14
The first is yellow and the second is black
Sice the balls are not replaced, we have
P(Yellow and black) = 5/8 * 2/7
P(Both Yellow) = 5/28
One is yellow the other is black
Sice the balls are not replaced, we have
P(One Yellow and One black) = 5/8 * 2/7 * 2
P(One Yellow and One black) = 5/14
They are of the same colour
Here, we have
P(Same) = 3/28 + 5/14
P(Same) = 13/28
Read more about probability at
https://brainly.com/question/251701
#SPJ1
Which choice is equivalent to the product below for acceptable values of x?
√x+3x-3
OA.√√-9
B. √+9
O C. √x²
O D. X

Answers
The equivalent to the product of the expression √(x + 3 ) × √(x - 3 ) is √( x² - 9 ).
What is the equivalent to the product of the given expression?Given the expression in the question;
√(x + 3 ) × √(x - 3 )
To multiply, we use combine using the product rule for radicals.
If two terms are contained in radicals, you can combine them under the same radical symbol if the index is the same.
Hence;
√(x + 3 ) × √(x - 3 ) = √( x + 3)( x - 3 )
Next. we expand the bracket using FOIL method.
√( x + 3)( x - 3 )
√( x( x - 3 ) + 3( x - 3 ) )
√( x² - 3x + 3x - 9 )
Simplify
Add -3x and 3x
√( x² - 9 )
Therefore, the equivalent expression is √( x² - 9 ).
Option A) √( x² - 9 ) is the correct answer.
Learn more about product and quotient rule for radicals here: https://brainly.com/question/30472558
#SPJ1