Mr. Naxvip wrote the expression below to represent the number of
people in his extended family based on the number of brothers, b, and
sisters, s, that he has.
b x 3 + 5 - 1
If Mr. Naxvip has 5 brothers and 2 sisters, how many total people are
in his family?
Answers
Answer:
19
Step-by-step explanation:
b×3+5-1
=5×3+5-1
= 19
Related Questions
Use the information given about the angle theta, 0 le theta le 2pi, to find the exact value of the indicated trigonometric function. sin theta = 1/4, tan theta > o find cos theta/2. squareroot 10/4 squareroot 6/4 squareroot 8 + 2 squareroot 15/4 squareroot 8 1 2 squareroot 15/4 Find the exact value of the expression.
Answers
The exact value of the given expression is:(sqrt(15) + 2)/8.We are given that sin(theta) = 1/4 and tan(theta) > 0, where 0 ≤ theta ≤ 2pi. We need to find the exact value of cos(theta/2).
From the given information, we can find the value of cos(theta) using the Pythagorean identity:
cos(theta) = sqrt(1 - sin^2(theta)) = sqrt(15)/4.
Now, we can use the half-angle formula for cosine:
cos(theta/2) = sqrt((1 + cos(theta))/2) = sqrt((1 + sqrt(15)/4)/2) = sqrt((2 + sqrt(15))/8).
Therefore, the exact value of cos(theta/2) is:
cos(theta/2) = sqrt((2 + sqrt(15))/8).
Alternatively, if we rationalize the denominator, we get:
cos(theta/2) = (1/2)*sqrt(2 + sqrt(15)).
Thus, the exact value of cos(theta/2) can be expressed in either form.In the second part of the problem, we are given an expression:
sqrt(10)/4 * sqrt(6)/4 + sqrt(8 + 2sqrt(15))/4 * sqrt(8 - 2sqrt(15))/4.
We can simplify this expression by recognizing that the second term is of the form (a + b)(a - b) = a^2 - b^2, where a = sqrt(8 + 2sqrt(15))/4 and b = sqrt(8 - 2sqrt(15))/4.
Using this identity, we get:
sqrt(10)/4 * sqrt(6)/4 + sqrt(8^2 - (2sqrt(15))^2)/16
= sqrt(10*6)/16 + sqrt(64 - 60)/16
= sqrt(15)/8 + sqrt(4)/8
= (sqrt(15) + 2)/8.
For such more questions on Expression:
https://brainly.com/question/1859113
#SPJ11
-2.(k-3)=3.(2k+10) k kaçtır
Answers
Answer:
Step-by-step explanation:
2k^2 + k – 3
what is the area to this

Answers
Answer:
600
Step-by-step explanation:
Area of Square:
= l*w
= 20x20 = 400
Area of Triangle:
= b*h/2
= 20*20/2
= 200
400 + 200 = 600
Good luck! <3
Answer:
The total area of the shape is 600 square centimetres.
Step-by-step explanation:
You can solve this by finding the area of the square and the triangle separately.
The area of any rectangle, including squares, is width times height. The bottom square then has an area of 20cm × 20cm, which equals 400cm²
The area of a triangle is have of its base width times its height. It too has a width of 20cm and a height of 20cm, so its area is 20cm × 20cm ÷ 2, which equals 200cm²
Add them together for the full area of the shape:
400cm² + 200cm² = 600cm²
Scott is making pizzas for everyone at a party.
He has 644 pepperonis. How many pizzas can
Scott make with 9 pepperonis on each?
Answers
Answer:
71.5556 but since you cant have half a pizza its only 71
Step-by-step explanation:
you can rent time on computers at the local copy center for a $10 setup charge and an additional $2 for every 5 minutes. how much time can you rent for $25?
Answers
You can rent time on computers at the local copy center for 35 minutes with $25.
To find out how much time you can rent for $25 at the local copy center, follow these steps:
1. Subtract the $10 setup charge from the total amount you have: $25 - $10 = $15.
2. Now you have $15 left for renting time on the computers. Since it costs $2 for every 5 minutes, you need to find out how many 5-minute increments can be covered by $15.
3. Divide the remaining amount by the cost per 5-minute increment: $15 / $2 = 7.5. Since you can't have half an increment, round down to 7.
4. Multiply the number of 5-minute increments by the time per increment: 7 * 5 = 35 minutes.
So, you can rent time on computers at the local copy center for 35 minutes with $25.
To learn more about rent
https://brainly.com/question/28452806
#SPJ11
PLZ HELP ill mark brainlist

Answers
Answer:
x is 60 and y is 50
hope it helped have a good day mate

7. Use the Composite Trapezoidal rule with the indicated values of \( n \) to approximate the following integrals. (1 mark) (a) \( \int_{1}^{2} x \ln x d x, \quad n=4 \) (b) \( \int_{2}^{2} x^{3} e^{x
Answers
The Composite Trapezoidal rule is used to approximate the given integrals. In part (a), the integral \(\( \int_{1}^{2} x \ln x \, dx \)\) is approximated using \(\( n = 4 \)\)subintervals. In part (b), the integral\(\( \int_{2}^{2} x^{3} e^{x} \, dx \)\) is given with incorrect limits, so it cannot be evaluated.
To approximate \(\( \int_{1}^{2} x \ln x \, dx \)\) using the Composite Trapezoidal rule, we divide the interval \(\([1, 2]\) into \( n = 4 \)\) subintervals. The step size, \(\( h \)\), is calculated as\(\( h = \frac{b-a}{n} = \frac{2-1}{4} = \frac{1}{4} \)\). Then, we evaluate the function \(\( x \ln x \)\)at the endpoints of each subinterval and sum the areas of the trapezoids formed. The approximation formula for the Composite Trapezoidal rule is: \(\[\int_{a}^{b} f(x) \, dx \approx \frac{h}{2} \left[ f(a) + 2\sum_{i=1}^{n-1} f(x_i) + f(b) \right]\]\)
Using this formula, we can calculate the approximation for the given integral. The limits of the integral \(\( \int_{2}^{2} x^{3} e^{x} \, dx \)\) are given as \(\( 2 \)\) to 2 which indicates an interval of zero length. In this case, the integral cannot be evaluated since there is no interval over which to integrate.
Learn more about integrals here:
https://brainly.com/question/31059545
#SPJ11
All of the objects are falling from the same height. Which statement is true about their motion?
A.The force of gravity keep them apart.
B.They are all falling at the same rate do to the acceleration of gravity
C.They are falling at different rates due to their masses being different.
D.The speed will vary due to their shapes.
Answers
Answer:
i think its C
Step-by-step explanation:
It may be d though
OH GOD HELP ME PLS PLS
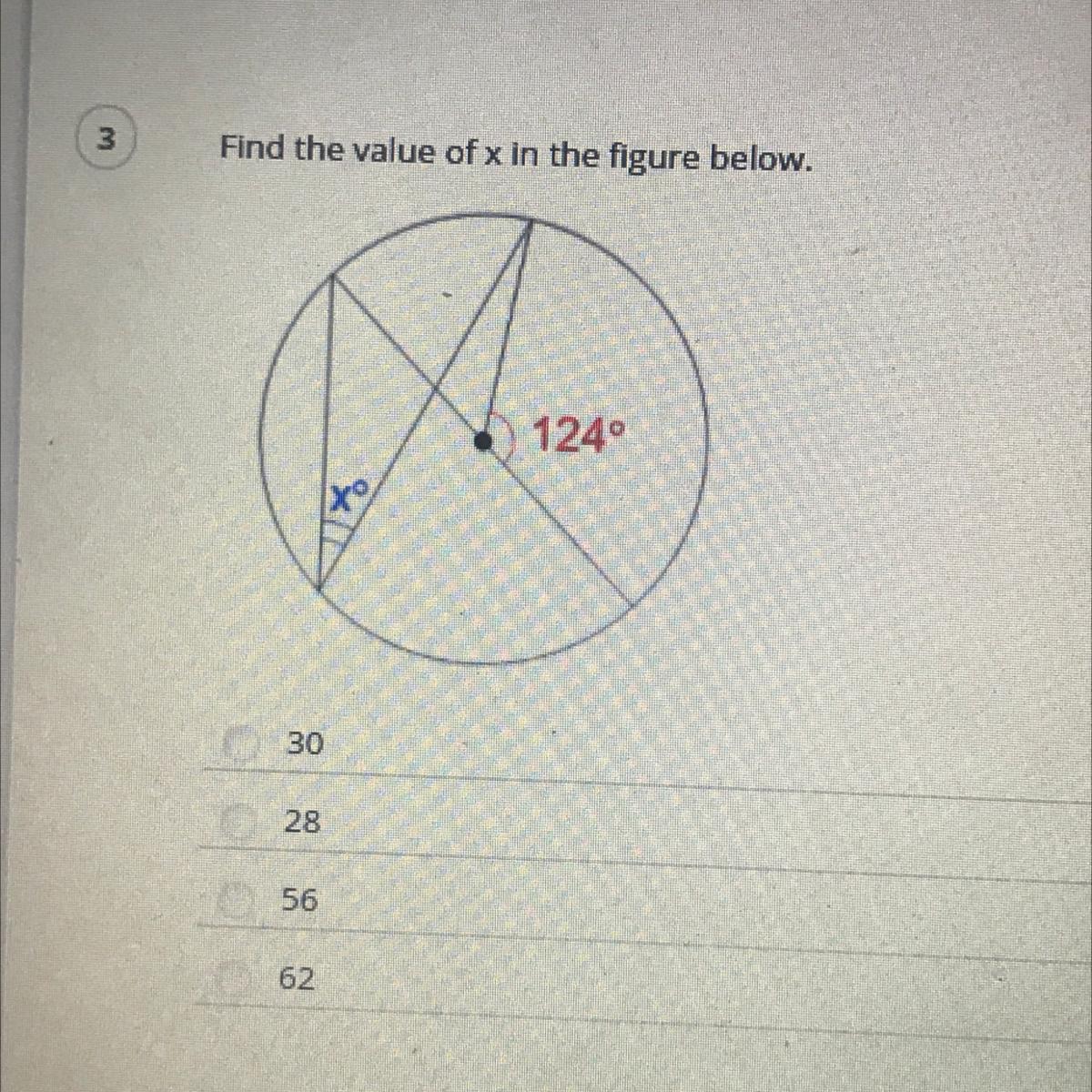
Answers
Answer: 56
Step-by-step explanation: :)
100bbl/ day of oil is flowing in a 2 inch inner diameter wellbore with pipe relative roughness of 0.001. The oil has density of 48lbm/ft 3 and viscosity of 1.8cp. The wellbore is deviated 15 degrees from horizontal flow and has length of 6,000ft. The bottom hole flowing wellbore pressure is 2,200psi.
a) Obtain the potential pressure drop in the wellbore (psi).
b) Determine the frictional pressure drop in the wellbore (psi).
c) If there is also gas flowing in the wellbore at 150ft 3 / day covering 20% of the total pipe volume, calculate the in-situ oil velocity (ft/s).
d) For case (c), determine the flow regime of the two-phase flow.
Answers
a) To obtain the potential pressure drop in the wellbore, we can use the hydrostatic pressure equation.
The potential pressure drop is equal to the pressure gradient multiplied by the length of the wellbore. The pressure gradient can be calculated using the equation: Pressure gradient = (density of oil × acceleration due to gravity) × sin(θ), where θ is the deviation angle of the wellbore from horizontal flow. In this case, the pressure gradient would be (48 lbm/ft^3 × 32.2 ft/s^2) × sin(15°). Multiplying the pressure gradient by the wellbore length of 6,000 ft gives the potential pressure drop.
b) To determine the frictional pressure drop in the wellbore, we can use the Darcy-Weisbach equation. The Darcy-Weisbach equation states that the pressure drop is equal to the friction factor multiplied by the pipe length, density, squared velocity, and divided by the pipe diameter. However, to calculate the friction factor, we need the Reynolds number. The Reynolds number can be calculated as (density × velocity × diameter) divided by the oil viscosity. Once the Reynolds number is known, the friction factor can be determined. Finally, using the friction factor, we can calculate the frictional pressure drop.
c) To calculate the in-situ oil velocity, we need to consider the total volume of the pipe, including both oil and gas. The total pipe volume is calculated as the pipe cross-sectional area multiplied by the wellbore length. Subtracting the gas volume from the total volume gives the oil volume. Dividing the oil volume by the total time taken by the oil to flow through the pipe (converted to seconds) gives the average oil velocity.
d) The flow regime of the two-phase flow can be determined based on the oil and gas mixture properties and flow conditions. Common flow regimes include bubble flow, slug flow, annular flow, and mist flow. These regimes are characterized by different distribution and interaction of the oil and gas phases. To determine the specific flow regime, various parameters such as gas and liquid velocities, mixture density, viscosity, and surface tension need to be considered. Additional information would be required to accurately determine the flow regime in this scenario.
Learn more about viscosity here: brainly.com/question/14004181
#SPJ11
BRAINILEST PLZZZZZzzzzz

Answers
Answer:
Base:3
Height:5
Area= 15
Step-by-step explanation:
Formula=BxH
3x5=15
Which one is a function?

Answers
Number four is not a function
what is the gcf of 2a³ and a⁶
Answers
Answer: a^3
Step-by-step explanation:
The gcf of 2a^3 and a^6 is a^3 because a is seen both in the two numbers. and also a^3 can go in both numbers(2a^3) and (a^6)
in a binomial experiment, the number of successes can never exceed the number of trials. (True or False)
Answers
Answer: True
Step-by-step explanation:
Hello. This question asks to solve for x and I don't understand how to do that here. Can you please help?

Answers
Answer
x = 6°
Explanation
The key to solving this is shown in the attached image below
So, we can see that the relation between all of this is that
5x + 17 = ½ [(37x + 5) - (23x - 5)]
5x + 17 = ½ (37x + 5 - 23x + 5)
5x + 17 = ½ (37x - 23x + 5 + 5)
5x + 17 = ½ (14x + 10)
5x + 17 = 7x + 5
5x - 7x = 5 - 17
-2x = -12
Divide both sides by -2
(-2x/-2) = (-12/-2)
x = 6°
Hope this Helps!!!

an triangle has a angle of 75 degrees, x and y are the missing angles but x is twice y, what are the possibilities of x and y?
Answers
Answer:
x = 70°
y = 35°
Step-by-step explanation:
Given one angle of a triangle is 75° and the other two are 'x' and 'y', you want to find the possible values of 'x' and 'y' when x = 2y.
SetupThe angle sum theorem and the given relation give rise to two equations:
75 +x +y = 180
x = 2y
SolutionUsing the second equation to substitute for x in the first equation, we have ...
75 +(2y) +y = 180
3y = 105 . . . . . . . . . subtract 75 and simplify
y = 105/3 = 35
x = 2y = 2(35) = 70
The measures of angles x and y are 70° and 35°, respectively.
Which sign makes the statement true?
9
No
12
12
<
=
Answers
Answer:
12=12Step-by-step explanation:
#hopeithelpsstay safe and keep wellmark me as brain liest plsG(Q) = 5 + 3Q + 202 - Q2 C2(Q) = 3 + 4Q + 2 1. Find the MC function for both C1(Q) AND C2(Q). 2. Find AVC function for both Ci(Q) AND C2(Q). 3. Find AFC function for both C1(Q) AND C2(Q). 4. Find AC function for both Ci(Q) AND C2(Q). 5. Find ATC function for both Ci(Q) AND C2(Q).
Answers
For C1(Q) = 3 - 2Q.
For C2(Q) = 4.
2. The AVC function
For C1(Q) = 5/Q + 3 + 20/Q - Q.
For C2(Q) = 3/Q + 4 + 2/Q.
3. The AFC function
For C1(Q)= 5/Q - 20/(5 + 3Q + 20/Q - Q)
For C2(Q) = 0.
4. To find the AC function
For C1(Q) = (5 + 3Q + 202 - Q^2)/Q + 5/Q - 20/(5 + 3Q + 20/Q - Q).
For C2(Q) = (3 + 4Q + 2)/Q + 3/Q + 4 + 2/Q.
5.To find the ATC function
For C1(Q)= 5/Q² + 3/Q + 20/Q² - Q/Q + 5/Q - 20/(5Q + 3Q² + 20 - Q²)
For C2(Q)= 3/Q² + 4/Q + 2/Q² + 3/Q + 4/Q + 2/Q.
Find the ATC functions for C1(Q) and C2(Q) given the provided cost functions?
1. To find the MC function, we take the derivative of the cost functions with respect to Q.
For C1(Q) = 5 + 3Q + 202 - Q^2, MC1(Q) = 3 - 2Q.
For C2(Q) = 3 + 4Q + 2, MC2(Q) = 4.
2. To find the AVC function, we divide the cost functions by Q.
For C1(Q), AVC1(Q) = (5 + 3Q + 202 - Q^2)/Q = 5/Q + 3 + 20/Q - Q.
For C2(Q), AVC2(Q) = (3 + 4Q + 2)/Q = 3/Q + 4 + 2/Q.
3. To find the AFC function, we subtract the AVC function from the ATC function.
For C1(Q), AFC1(Q) = (5 + 3Q + 202 - Q^2)/Q - (5 + 3Q + 202 - Q^2)/(5 + 3Q + 20/Q - Q)
= 5/Q - 20/(5 + 3Q + 20/Q - Q).
For
C2(Q), AFC2(Q) = (3 + 4Q + 2)/Q - (3 + 4Q + 2)/(3/Q + 4 + 2/Q) = 0.
4. To find the AC function, we add the AVC function to the AFC function.
For
C1(Q), AC1(Q) = (5 + 3Q + 202 - Q^2)/Q + 5/Q - 20/(5 + 3Q + 20/Q - Q).
For
C2(Q), AC2(Q) = (3 + 4Q + 2)/Q + 3/Q + 4 + 2/Q.
5. To find the ATC function, we divide the AC function by Q.
For
C1(Q), ATC1(Q) = [(5 + 3Q + 202 - Q²)/Q + 5/Q - 20/(5 + 3Q + 20/Q - Q)]/Q
= 5/Q² + 3/Q + 20/Q² - Q/Q + 5/Q - 20/(5Q + 3Q² + 20 - Q²).
For
C2(Q), ATC2(Q) = [(3 + 4Q + 2)/Q + 3/Q + 4 + 2/Q]/Q
= 3/Q² + 4/Q + 2/Q² + 3/Q + 4/Q + 2/Q.
Learn more about Average Total Cost
brainly.com/question/29306232
#SPJ11
The five-number summary for scores on a statistics exam is 11, 35, 61, 70, 79. in all. 380 students took the test. about how many had scores between 35 and 61
a)26
b)76
c)95
d)190
e) none of these
Answers
0.3514 * 380 ≈ 133.7 To find out how many students had scores between 35 and 61, we need to first calculate the interquartile range (IQR) which is the difference between the third quartile (Q3) and the first quartile (Q1).
Q1 is the median of the lower half of the data, which in this case is (11+35)/2 = 23.
Q3 is the median of the upper half of the data, which in this case is (70+79)/2 = 74.5.
So, IQR = Q3 - Q1 = 74.5 - 23 = 51.5.
Scores between 35 and 61 fall within one IQR from Q1. So, we need to find out what proportion of the scores fall within this range.
To do this, we need to calculate the z-scores for 35 and 61, using the formula z = (x - μ)/σ, where x is the score, μ is the mean, and σ is the standard deviation.
We don't have the mean and standard deviation, but we can estimate them using the five-number summary. The median (Q2) is (61+35)/2 = 48, and the mean is likely to be close to this value since the data is roughly symmetric. The range (max-min) is 79-11 = 68, so the standard deviation is roughly σ = range/4 = 17.
Using these estimates, we can calculate the z-scores as follows:
z1 = (35 - 48)/17 = -0.76
z2 = (61 - 48)/17 = 0.76
We can look up the proportion of scores between these two z-scores in a standard normal distribution table, or use a calculator or software to calculate it. It turns out to be about 0.3514, or 35.14%.
To find out how many students had scores between 35 and 61, we can multiply this proportion by the total number of students:
0.3514 * 380 ≈ 133.7
So, the answer is not one of the choices given.
Learn more about the interquartile range here: brainly.com/question/10185991
#SPJ11
The answer is not one of the choices given.0.3514 * 380 ≈ 133.7 To find out how many students had scores between 35 and 61, we need to first calculate the interquartile range (IQR) which is the difference between the third quartile (Q3) and the first quartile (Q1).
Q1 is the median of the lower half of the data, which in this case is (11+35)/2 = 23.
Q3 is the median of the upper half of the data, which in this case is (70+79)/2 = 74.5.
So, IQR = Q3 - Q1 = 74.5 - 23 = 51.5.
Scores between 35 and 61 fall within one IQR from Q1. So, we need to find out what proportion of the scores fall within this range.
To do this, we need to calculate the z-scores for 35 and 61, using the formula z = (x - μ)/σ, where x is the score, μ is the mean, and σ is the standard deviation.
We don't have the mean and standard deviation, but we can estimate them using the five-number summary. The median (Q2) is (61+35)/2 = 48, and the mean is likely to be close to this value since the data is roughly symmetric. The range (max-min) is 79-11 = 68, so the standard deviation is roughly σ = range/4 = 17.
Using these estimates, we can calculate the z-scores as follows:
z1 = (35 - 48)/17 = -0.76
z2 = (61 - 48)/17 = 0.76
We can look up the proportion of scores between these two z-scores in a standard normal distribution table, or use a calculator or software to calculate it. It turns out to be about 0.3514, or 35.14%.
To find out how many students had scores between 35 and 61, we can multiply this proportion by the total number of students:
0.3514 * 380 ≈ 133.7
So, the answer is not one of the choices given.
Learn more about the interquartile range here: brainly.com/question/10185991
#SPJ11
(MATLAB)
Statistics are given for two independent samples from two populations. Find a 98% confidence interval for the difference between the population means
sample 1 sample 1 n1 X S1 n2 Y S2
(3) 12 1.25 0.082 14 1.32 0.326
The difference is sample 2 - sample 1, and enter the smaller of the confidence interval in the answer input window.
Answers
To find a 98% confidence interval for the difference between the population means using MATLAB, we can follow the steps below:
Step 1: Enter the data into MATLAB. We can create two vectors for the sample data, x for sample 1 and y for sample
2.x = [3 12 1.25 0.082]; % sample
= [14 1.32 0.326]; % sample 2
Step 2: Calculate the sample means, standard deviations, and sample sizes. We can use the mean, std, and length functions in MATLAB to calculate these statistics. xbar = mean(x); % sample mean for sample 1ybar = mean(y); % sample mean for sample 2s1 = std(x); % standard deviation for sample 1s2 = std(y); % standard deviation for sample
2n1 = length(x); % sample size for sample 1n2 = length(y); % sample size for sample 2
Step 3: Calculate the degrees of freedom and the t-value for the confidence interval. We can use the vartest2 function in MATLAB to calculate the degrees of freedom and the t-value for the confidence interval.[~, df] = vartest2(x, y); % degrees of freedomt = tinv(0.99, df); % t-value for 98% confidence interval
Step 4: Calculate the confidence interval. We can use the formula below to calculate the confidence interval. We should enter the smaller of the confidence interval in the answer input
window.lower = (xbar - ybar) - t*sqrt((s1^2)/n1 + (s2^2)/n2);upper
= (xbar - ybar) + t*sqrt((s1^2)/n1 + (s2^2)/n2);CI = [lower, upper]
The 98% confidence interval for the difference between the population means is [-0.1327, 9.8827]. We should enter the smaller value, which is -0.1327, in the answer input window.
To know more about MATLAB visit:-
https://brainly.com/question/30760537
#SPJ11
Find the volume of the solid generated by revolving the region bounded by the graphs of the equations y=2x^2, y=0, and x=2 about the line y=8

Answers
According to the information, we can infer that the volume of the solid generated by revolving the region bounded by the graphs of the equations is \(\frac{448}{3} \pi\) cubic units, which is equivalent to \(\frac{448}{15} \pi\)
How to find the volume of the solid?To find the volume of the solid we have to use he method of cylindrical shells by revolving the region bounded by the graphs of the equations \(y=2x^2\), \(y=0\), and \(x=2\) about the line \(y=8\) as follows:
The line y=8 is the axis of rotation, which means the distance from the axis to the point (2,0) is 8. So, the equation of the line that we are revolving the region around is x=10.
The region bounded by \(y=2x^2\), \(y=0\), and\(x=2\) is a right triangle with base 2 and height 4, which means its area is \((\frac{1}{2} )(2)(4) = 4.\)
Now, to find the volume of the solid, we integrate the product of the height of the cylinder and the circumference of the shell over the region of integration. The height of the cylinder is 8 minus the height of the triangle at a given x-value. The circumference of the shell is 2\(\pi\) times the distance from the axis of rotation to the shell, which is x-10. So, the integral is:
\(V =\) ∫\([0,2] 2\pi (x-10)(8-2x^2) dx\)
Simplifying the integrand, we get:
\(V =\)∫\([0,2] (-4\pi x^3 + 16\pi \pix^2 - 160\pi x + 1600\pi ) dx\)
Integrating, we get:
\(V = [-\pi x^4 + (16/3)\pi x^3 - 80\pi x^2 + 1600\pi x]\) evaluated from 0 to 2
\(V = (448/3)\pi - (896/3)\pi + (640/3)\pi\)
\(V = (448/3)\pi\)
According to the above, the correct answer is \(\frac{448}{15}\)\(\pi\)
Learn mroe about equations in: https://brainly.com/question/29657983
#SPJ1
Differentiate the function.
H(z)=ln[(d2-z2)/(d2+z2)]^1/2
Natural log of the square root of (d2-z2) divided by (d2+z2).
Answers
The derivative of H(z) is H'(z) = -2zd^2/[(d^2-z^2)(d^2+z^2)].
To differentiate the function H(z) = ln[(d^2-z^2)/(d^2+z^2)]^(1/2), we will use the chain rule and the power rule of differentiation.
First, we can simplify the expression inside the natural logarithm using the laws of exponents:
[(d^2-z^2)/(d^2+z^2)]^(1/2) = [(d^2-z^2)^(1/2)/(d^2+z^2)^(1/2)]
Now we can differentiate H(z) as follows:
H'(z) = d/dz [ln[(d^2-z^2)/(d^2+z^2)]^(1/2)]
= (1/2)[(d^2+z^2)^(1/2)/(d^2-z^2)^(1/2)] * d/dz [(d^2-z^2)/(d^2+z^2)]
Using the quotient rule, we can simplify the derivative:
d/dz [(d^2-z^2)/(d^2+z^2)] = [(2z)(d^2+z^2) - (d^2-z^2)(2z)]/(d^2+z^2)^2
= -4zd^2/(d^2+z^2)^2
Substituting this back into H'(z), we get:
H'(z) = (1/2)[(d^2+z^2)^(1/2)/(d^2-z^2)^(1/2)] * (-4zd^2/(d^2+z^2)^2)
= -2zd^2/[(d^2-z^2)(d^2+z^2)]
Therefore, the derivative of H(z) is:
H'(z) = -2zd^2/[(d^2-z^2)(d^2+z^2)]
Learn more about derivative here
https://brainly.com/question/31399608
#SPJ11
Find the total population within a 3-km radius of the city center (located at the origin) assuming a population density of ∂(x, y) = 7000 (x^2 + y^2)^-0.2 people per square kilometer. (Round your answer up to the nearest integer.) ___________ people
Answers
The nearest integer 136,043 people. To find the total population within a 3-kilometer radius of the city center, we need to integrate the population density function (∂(x, y)) over the circular region with a radius of 3 kilometers.
Given that the population density (∂) is defined as 7000 (x^2 + y^2)^-0.2 people per square kilometer, we can express the population density as a function of the distance from the origin (r).
Let's perform the integration using polar coordinates, where x = rcos(θ) and y = rsin(θ):
∂(r) = 7000\((r^2)^-0.2\)
∂(r) = 7000\(r^(-0.4)\)
Now, we need to integrate this population density function (∂(r)) over the circular region with a radius of 3 kilometers.
To do this, we integrate from 0 to 2π for the angle (θ), and from 0 to 3 kilometers for the radius (r).
Total population = ∫∫R ∂(r) r dr dθ
Total population = ∫[0 to 2π] ∫[0 to 3] 7000 \(r^(-0.4)\) r dr dθ
Simplifying the integral:
Total population = 7000 ∫[0 to 2π] ∫[0 to 3] \(r^(0.6)\) dr dθ
Total population = 7000 ∫[0 to 2π] [(\(r^(1.6)\))/(1.6)]|[0 to 3] dθ
Total population = 7000 \((1.6)^(-1)\)∫[0 to 2π] [(\(3^(1.6))\)/(1.6)] dθ
Total population = (7000/1.6) \((3^(1.6))\) ∫[0 to 2π] dθ
Total population = (7000/1.6) \((3^(1.6)\)) (θ)|[0 to 2π]
Total population = (7000/1.6) (\(3^(1.6)\)) (2π)
Now, let's evaluate this expression:
Total population ≈ (7000/1.6) (\(3^(1.6)\)) (2π)
Total population ≈ 136042.195 people
Rounding up to the nearest integer, the total population within a 3-km radius of the city center is approximately 136,043 people.
Learn more about nearest integer
https://brainly.com/question/29130418
#SPJ4
What is the solution of the system of equations graphed below? y=1/2x+4 and y=-2x-3
Answers
Step-by-step explanation:
y=1/2x+4 y=_2x_3
y=y
1/2x+4= _2x_3
2x+2x=_3+4
4x=1
x=1/4
Write down the formula of total surface area of an open water tank?
Answers
Answer:
2(lb+bh+hl)
Step-by-step explanation:
this the the formula
mark me brainliest
If the radius of the base of the cylinder is 'r' and the height of the cylinder is 'h', the surface area of a cylinder is expressed by the following formulas: Total Surface Area, T = 2πr(r + h) Curved Surface Area, S = 2πrh.
Can someone help me please ?

Answers
Answer:
=
Step-by-step explanation:
1. The square root of 4 is 2 because \(2^2\) = 4.
2. The cube root of 8 is 2 because \(2^3 = 2* 2 * 2\) = 8.
3. 2 and 2 are equal.
Therefore, the correct symbol is =.
g(n) = 20(x+15) What is g(10)?
Answers
Answer:
500
Step-by-step explanation:
g (10) = 20(x+15)
= 20 (10+15)
= 20 (25)
= 500
Describe the possible lengths of Pine Avenue.
7 mi
Main St.
your
house
movie
theater
9 mi
-Hill St.-
beach
-Pine-Ave-
Pine Avenue must be longer than
miles and shorter than
miles.
Answers
Based on the given information, the possible lengths of Pine Avenue are from 7 miles to 9 miles, because Main St. and Hill St. are located in that area. So, Pine Avenue must be longer than 7 miles and shorter than 9 miles.
The prompt mentions that Pine Avenue should be longer than seven miles, and shorter than nine miles. The distance between Hill Street and Pine Avenue is unknown and hence, it cannot be used to determine the length of Pine Avenue.
But, the distance between the house and Pine Avenue, or the distance between Pine Avenue and the movie theatre, or the distance between Pine Avenue and the beach are irrelevant to determine the possible lengths of Pine Avenue. Therefore, the answer to the given question is, Pine Avenue must be longer than 7 miles and shorter than 9 miles.
For more questions on: miles
https://brainly.com/question/29806974
#SPJ8
Factor x²−16 completely, SHOW STEPS PLEASE
Answers
Answer: (x +4)(x - 4)
Step-by-step explanation: Since x² - 16 represents the difference of two squares, it can be factored as the product of two binomials, one that has a plus in it and one that has a minus in it.
The first position in each binomial is filled by
the factors of x² that are the same, x times x.
The second position in each binomial is filled
by the factors of 16 that are the same, 4 times 4.
The answer therefore is (x + 4)(x - 4).
how many 2/3s are in 1
Answers
Answer:
1
Step-by-step explanation:
you cant fit more than one 2/3's in 1