PLEASE HELP ME I’LL GIVE BRILLIANCE TO YOU (it’s question 16)

Answer:

0.77 or 77%

Step-by-step explanation:

Given:

Percentage of brown peanuts = 12%

Percentage of yellow peanuts = 15%

Percentage of red peanuts = 12%

Percentage of blue peanuts = 23%

Percentage of orange peanuts = 23%

Percentage of green peanuts = 15%

Total = 0.12 + 0.15 + 0.12 + 0.23 + 0.23 + 0.15 = 1

Probability that a randomly selected peanut M&M is not orange:

P(orange)' = 1 - P(orange)

Where,

P(orange) = 23% = 0.23

Thus,

P(orange)' = 1 - 0.23

P(orange) ' = 0.77

Probability that a randomly selected peanut is not orange = 0.77

Answer:

The mean weight of an adult is 66 kilograms with a variance of 144. If 123 adults are randomly selected, the sample mean would follow a normal distribution with a mean of 66 kilograms and a standard deviation of sqrt(144/123) = 3/sqrt(123) kilograms.

We can standardize the sample mean to find the probability that it would be greater than 66.7 kilograms. The standardized value for 66.7 is (66.7 - 66) / (3/sqrt(123)) = 2.3094.

Using a standard normal distribution table, we find that the probability of a standard normal variable being greater than 2.3094 is approximately 0.0104.

Therefore, the probability that the sample mean would be greater than 66.7 kilograms is approximately 0.0104, rounded to four decimal places.

Step-by-step explanation:

Answer:

Step-by-step explanation:

Given :-

To Find :-

We can find the slope of the line passing through the points \(( x_1,y_1)\) and \(( x_2,y_2)\)as ,

\(\implies m = \dfrac{ y_2-y_1}{x_2-x_{1}}\)

\(\implies m = \dfrac{ 42-15}{18-7} \\\\\implies \boxed{ m = \dfrac{ 27}{11 }}\)

Hence the slope of the line is 27/11 .

\(\rule{200}2\)

Finding the length of AB :-

\(\implies Distance =\sqrt{ (x_2-x_1)^2+(y_2-y_1)^2} \\\\\implies Distance =\sqrt{ (18-7)^2+(42-15)^2 } \\\\\implies Distance =\sqrt{ 11^2 + 27^2 } \\\\\implies Distance =\sqrt{ 121 + 729 } \\\\\implies Distance = \sqrt{ 850} \\\\\implies \boxed{ Distance = 29.15 \ units }\)

Hence the length of AB is 29.15 units .

(a)image averaging is a very effective method of reducing noise in images. Image averaging reduces noise by adding multiple images of the same scene together and then dividing by the number of images added.The conditions that must be fulfilled for the image averaging method are as follows:-

(i) The background of the image must not move between each image capture.- The noise present in the image must be random.- The source of the noise must be consistent.

(ii)The mathematical expression that characterizes the noise in the resultant image when K images are averaged, as K becomes large is given by;sigma_n^2/K

Where;sigma_n^2 is the variance of the noise and K is the number of images that have been averaged.

Therefore, as K increases, the variance of the noise in the resultant image reduces, and thus, the noise reduces.When either method can be used for noise reduction, the temporal image averaging method would be the preferred method to select.

(iii)This is because it uses a sequence of images that are taken at different times, usually at high speeds, to produce a single image that is free of noise. This method is best when dealing with fast-moving objects, and it can be used in situations where the camera cannot be stabilized and is experiencing unwanted vibration or shaking.

Learn more about image averaging here https://brainly.com/question/29043541

#SPJ11

3/2 and -5 is the measure of x from the logarithmic equation

Given the logarithmic equation

log₁₁(2x-1)=1-log₁₁ (x+4)

Since log₁₁11 = 1, the equation will become

log₁₁(2x-1) = log₁₁11 -log₁₁ (x+4)

log₁₁(2x-1) = log₁₁11/x+4

Cancelling log₁₁ on both sides

2x - 1 = 11/x + 4

2x - 1(x+4) = 11

2x²+8x-x-4 = 11

2x² + 7x - 15 =0

Factorize the result to have:

2x² + 7x - 15 =0

2x² + 10x - 3x - 15 = 0

2x(x+5) - 3(x+5) = 0

2x - 3 = 0 and x + 5 = 0

x = 3/2 and -5

Hence the measure of the value of x from the equation is 3/2 and -5

Learn more on logarithm here: https://brainly.com/question/25710806

#SPJ1

Answer:

Pythagorean Theorum

Step-by-step explanation:

a^2*b^2= c^2

correct answer is option C, i.e. vertical shrink by a factor of 1/6.

Given:

Two graphs are given, one is of f(x) = x^4 and other is of b(x)=6x^4.

Find:

we have to find the correct option.

Explanation:

when we transformed the graph

Answer: C. Sesame oil freezes at a lower temperature than peanut oil because −6.2 °C < 3.1 °C

Step-by-step explanation:

Given that:

Freezing point of sesame oil = - 6.2°C

Freezing point of peanut oil = 3.1°C

Comparing the two temperatures :

Freezing(when a substance turns to solid) usually occurs at low temperatures. The temperature of sesame oil(-6 2°C) is lower than that of peanut oil(3.1°C).

Hence, it can be concluded that Sesame oil freezes at lower temperature than peanut oil.

Mathematically,

-6.2°C < 3.1°C

Answer:

Answer: C. Sesame oil freezes at a lower temperature than peanut oil because −6.2 °C < 3.1 °C

Step-by-step explanation:

Answer:

24 ft.

Step-by-step explanation:

Radius = 4 ft

Central angle = 6°

Arc length = radius × central angle

= 4 × 6°

= 24 ft.

The given channel section is shown in the image below:  \(\frac{b}{2}\) = 9 in\(\frac{h}{2}\) = 7.5 in.  The centroid of the section is obtained by considering small rectangular strips of width dx and height y (measured from the x-axis) as shown below:

 \(\delta y\) = y \(\delta x\).

Since the centroid lies on the y-axis of the section, the x-coordinate of the centroid is zero. To find the y-coordinate, we can write the moment of the differential strip about the x-axis as shown below:

dM = \(\frac{t}{2}(b-dx)y\) dx where, dx is a small width of the differential strip.

Thus, the moment of the entire section about the x-axis is given by:

Mx = ∫dM = ∫\(\frac{t}{2}(b-dx)y\) dx \(^{b/2}_{-b/2}\)= \(\frac{t}{2}\)y[bx - \(\frac{x^2}{2}\)] \(^{b/2}_{-b/2}\)= \(\frac{tb}{2}\)y.

Thus, the y-coordinate of the centroid is given by:

yc = \(\frac{Mx}{A}\).

where A is the area of the section. Thus,

yc = \(\frac{\frac{tb}{2}y}{bt}\) \(\int\int\int_{section}\) dA= \(\frac{1}{2}\)yyc = \(\frac{1}{2}\) \(\int\int\int_{section}\) y dA= \(\frac{1}{2}\) [(2t)(h)(\(\frac{b}{2}\))] \(-\) [(2t)(0)(\(\frac{b}{2}\))]= \(\frac{bht}{2}\) / (bt) = \(\frac{h}{2}\) = 7.5 in.

Thus, the centroid of the section with respect to x and y-axis is at (0, 7.5) which is at a distance of 7.5 inches from the x-axis.

To know more about rectangular visit:

https://brainly.com/question/21416050

#SPJ11

Answer:

Here Is the Graph

Step-by-step explanation:

I will always suggest using Desmos Graphing Calculator

The graph of the inequality is attached.

A relationship between two expressions or values that are not equal to each other is called 'inequality'.

Given that the graph for the inequality,

-2x - y > 1

The graph is attached in answer.

For more references on inequality, click;

https://brainly.com/question/28823603

#SPJ2

Damian's percent error for the estimate of the time that Lily would play is of 47.37%.

The percent error is obtained applying the proportions in the context of the problem.

A proportion is applied as the percent error is given by the difference between the estimate and the actual value, divided by the actual value, and multiplied by 100%.

The parameters for this problem are given as follows:

Hence the percent error is given as follows:

P = (38 - 20)/38 x 100%

P = 47.37%.

More can be learned about proportions at https://brainly.com/question/24372153

#SPJ1

Answer:

I believe the correct answer would be 16.

Step-by-step explanation:

There are 2 cases of golf balls that hold 12 boxes of 12 balls.

    12(12) + 12(12) = 288

You need to find how many cases Joan can buy to equal the amount of 288 balls.

    18(x) = 288

I simply divided 288 by 18 to get the answer of 16.

    x = 16

The number of packages should need to buy is 16.

There are 2 cases of golf balls that hold 12 boxes of 12 balls.

12(12) + 12(12) = 288

Now

18(x) = 288

x = 16

Learn more: https://brainly.com/question/10309631?referrer=searchResults

Answer:

quadrant IV

Step-by-step explanation:

beacause 3 is all negative and 4 in mixed

Answer:

The location of the point is between Quadrant II and Quadrant III

Step-by-step explanation:

The constant of proportionality will be 6.

The general equation of a straight line is -

[y] = [m]x + [c]

where -

[m] → is slope of line which tells the unit rate of change of [y] with respect to [x].

[c] → is the y - intercept i.e. the point where the graph cuts the [y] axis.

We have a equation c = 6m represents how many ice cream cones (c) are sold within a certain number of minutes (m) at a certain ice cream shop

We can use the equation of a straight line to represent direct proportionality as -

y = mx + c

for -

c = 0

y = mx

m = y/x

Where [m] as constant of proportionality.

For -

c = 6m

constant of proportionality will be 6.

Therefore, the constant of proportionality will be 6.

To solve more questions on straight lines, visit the link below-

brainly.com/question/20400984

#SPJ1

Answer:

YEs tis i, the simplifier

Step-by-step explanation:

its 6

Answer:

ummmmmmmm

Step-by-step explanation:

Answer:

10x+5=y.

(SO, someone deleted my answer earlier)

Answer:

= 59​

Step-by-step explanation:

5 - 2 * 3 + 6 (3² + 1)

= 5 - 2 * 3 + 6 * 10

= 5 - 6 + 6 * 10

= 5 - 6 + 60

= 59​

Answer:

Step-by-step explanation:

\(5-2\times \:3+6\left(3^2+1\right)\\\\\mathrm{Follow\:the\:PEMDAS\:order\:of\:operations}\\\\\mathrm{Calculate\:within\:parentheses}\:\left(3^2+1\right)\::\quad 10\\\\=5-2\times \:3+6\times \:10\\\\\mathrm{Multiply\:and\:divide\:\left(left\:to\:right\right)}\:2\times \:3\::\quad 6\\=5-6+6\times \:10\\\\\mathrm{Multiply\:and\:divide\:\left(left\:to\:right\right)}\:6\times \:10\::\quad 60\\\\=5-6+60\\\\\mathrm{Add\:and\:subtract\:\left(left\:to\:right\right)}\:5-6+60\:\\\\:\quad 59\)

Answer:

Hi, the answer is a.

Step-by-step explanation:

1. 1800-200=1600

2. As 1800 is total x will be smaller amount. so....

3. when we write a subtraction statement bigger number - smaller number..

4. So answer will be 1600-x

The expression that represents the money left in his wallet in rupees will be 1600 - x. Then the correct option is A.

The equivalent is the expression that is in different forms but is equal to the same value.

The definition of simplicity is making something simpler to achieve or grasp while also making it a little less difficult.

Naren had Rs. 1800 in his wallet. He spent Rs. x on a watch and 200 to watch a cricket match.

Then the expression is given as,

⇒ 1800 - x - 200

Simplify the expression, then we have

⇒ 1800 - x - 200

⇒ 1600 - x

The expression that represents the money left in his wallet in rupees will be 1600 - x. Then the correct option is A.

More about the equivalent link is given below.

https://brainly.com/question/889935

#SPJ2

Using the fact that X is binomial with n = 800 and p = 0.5, we can find P(X > 350) by calculating 1 - P(X ≤ 350). This calculation can be done using the binomial probability formula, but it can also be done more easily using technology like GeoGebra. The result we get from GeoGebra is P(X > 350) ≈ 0.0003.

A fair coin is tossed 800 times, so X, the random variable representing the number of tails that appear, follows a binomial distribution with n = 800 and p = 0.5 (since the coin is fair, the probability of getting tails is 0.5).

To find P(X > 350), we can use the binomial probability formula:

P(X > 350) = 1 - P(X ≤ 350)

= 1 - ∑(k=0 to 350) [(800 choose k) * 0.5^800]

This calculation can be quite tedious to do by hand, but we can use technology like GeoGebra to help us with the calculation. Using GeoGebra, we can input the binomial distribution function with n = 800 and p = 0.5, and then use the cumulative probability feature to find P(X ≤ 350). Then, we can subtract this value from 1 to find P(X > 350).

The result from GeoGebra is P(X > 350) ≈ 0.0003.

To know more about binomial visit:-

https://brainly.com/question/30339327

#SPJ11

Answer:

x = 1.289

Step-by-step explanation:

11^x = 22

Take the log of both sides

xlog11 = log22

Divide both sides by log11

x = log22 / log11

Use calculator

x = 1.289

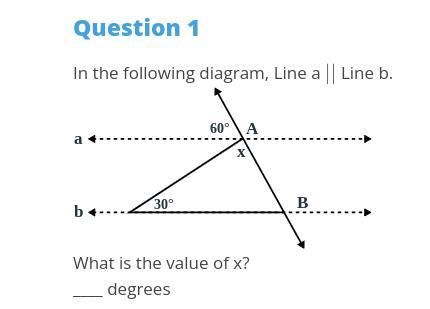
Answer:

since a || b

<A = <ABb = 60°

in a triangle the sum of all angles is 180°

so,

30 + 60 + x = 180

x= 180-90

x= 90

Answer:

Look below

Step-by-step explanation:

1) x = 14, because 14 * 14 = 196

2) x = 3 / 16, because ( 3 / 16 ) * ( 3 / 16 ) = 9 / 256

3) x = 8, because 8 * 8 * 8 = 512

4) x = 4 / 7, because ( 4 / 7 ) * ( 4 / 7 ) * ( 4 / 7 ) = 64 / 343

Answer:

x = 15

Step-by-step explanation:

3x-7=x+23

Subtract x from each side

3x-x-7=x-x+23

2x -7 = 23

Add 7 to each side

2x-7+7 = 23+7

2x = 30

Divide by 2

2x/2 = 30/2

x = 15

Answer:

x=15

Step-by-step explanation:

3x-x=23+7

2x=30 divide by 2

x=15

Answer:

Assuming you are solving for x:

x = 6 - y

Step-by-step explanation:

y = -x + 6

y + x = 6

x = 6 - y