Answers
Related Questions
Find all the complex roots. Leave your answer in polar form with the argument in degrees. The complex cube roots of 1 + i. 1) z0 = __ ( cos __° + i sin __º) (Simplify your answer, including any radicals. Type an exact answer, using radicals as needed. Type any angle measures in degrees.) 2) z0 = __ ( cos __º+i sin __º) (Simplify your answer, including any radicals. Type an exact answer, using radicals as needed. Type any angle measures in degrees.) 3) z0 = __ ( cos __º+ i sin º) (Simplify your answer, including any radicals. Type an exact answer, using radicals as needed. Type any angle measures in degrees.)
Answers
The complex cube roots of 1 + i are:
z0 = (sqrt(2))^(1/3) [cos(π/12) + i sin(π/12)]
z1 = (sqrt(2))^(1/3) [cos(7π/12) + i sin(7π/12)]
z2 = (sqrt(2))^(1/3) [cos(11π/12) + i sin(11π/12)]
To find the complex cube roots of 1 + i, we can express 1 + i in polar form and use De Moivre's theorem.
Step 1: Convert 1 + i to polar form.
We have:
r = sqrt(1^2 + 1^2) = sqrt(2)
θ = tan^(-1)(1/1) = π/4 (45 degrees)
So, 1 + i can be written as:
1 + i = sqrt(2) (cos(π/4) + i sin(π/4))
Step 2: Apply De Moivre's theorem.
De Moivre's theorem states that for any complex number z = r(cos(θ) + i sin(θ)) and any positive integer n, the complex nth roots of z are given by:
z0 = r^(1/n) [cos(θ/n + 2πk/n) + i sin(θ/n + 2πk/n)]
In this case, we are finding the cube roots (n = 3) of 1 + i.
For the first cube root (k = 0):
z0 = (sqrt(2))^(1/3) [cos((π/4)/3) + i sin((π/4)/3)]
= (sqrt(2))^(1/3) [cos(π/12) + i sin(π/12)]
For the second cube root (k = 1):
z1 = (sqrt(2))^(1/3) [cos((π/4 + 2π)/3) + i sin((π/4 + 2π)/3)]
= (sqrt(2))^(1/3) [cos(7π/12) + i sin(7π/12)]
For the third cube root (k = 2):
z2 = (sqrt(2))^(1/3) [cos((π/4 + 4π)/3) + i sin((π/4 + 4π)/3)]
= (sqrt(2))^(1/3) [cos(11π/12) + i sin(11π/12)]
Therefore, the complex cube roots of 1 + i are:
z0 = (sqrt(2))^(1/3) [cos(π/12) + i sin(π/12)]
z1 = (sqrt(2))^(1/3) [cos(7π/12) + i sin(7π/12)]
z2 = (sqrt(2))^(1/3) [cos(11π/12) + i sin(11π/12)]
To learn more about cube:
brainly.com/question/28134860
#SPJ11
Why is my engine knocking?
Answers
Answer: i agree with the other guy ↑
Help i have a question please help.

Answers
In the trigonometric function, f(x) = 7cos[2π(x + 9)/7] + 1, the direction and how many units is is shifted vertically is 1 unit up
What is a trigonometric function?A trigonometric function is an equation containing a trigonometric ratio
Given the trigonometric function f(x) = 7cos[2π(x + 9)/7] + 1, we want to compare it with the trigonometric equation f(x) = acos[2π(x + c)/b] + d, to find the vertical shift of the graph. We proceed as follows
Since we know that the general equation of a trigonometric function is f(x) = acos[2π(x + c)/b] + d where
a = amplitudec = phase shiftb = period andd = vertical shiftComaring both equations, we have that
a = 7c = 9b = 7 andd = 1So, we see that since d = + 1, we see that the function f(x) = 7cos[2π(x + 9)/7] + 1 is shifted vertically upwards by 1 unit.
So, the direction and how many units is is shifted vertically is 1 unit up
Learn more about trigonometric function here:
https://brainly.com/question/29718746
#SPJ1
PLEASE HELP ISTG I WILL MARK BRAINLIEST PLEASE NO SPAM OR RANDOM ANSWERS PLEASE I WILL DO ANYTHING

Answers
Answer:
I will say this idk if you learn by reading or watching better, so if it's reading then read on! but if it's watching then look up "how to graph lines" and there is a bunch of videos!
Step-by-step explanation:
so you have y = 3x - 2 so first on the y axis your start point will be (0, -2)
then refer to rise over run ( rise/run) where rise is up(on the y axis) and run is across on the x axis.
so you start at (o, -2) and up 3 points on the y axis and across 1 point (go left) and mark it and repeat( up 3 across 1) until you reach the top of the graph
then finish the graph so repeating this going to the bottom is the same but different directions:
so go back to (0, -2) and go down 3 points (y axis) and across 1 point(this time go right on the x axis) and repeat until you reach the bottom and then use the points you marked to trace a line and boom your done! (this explanation is only for number 10)
same rise over run but different points and possibly line direction.
so for number 11: your starting point is (0, 3) and you go up 4 point and across 1 point but this time go across to the right. repeat. once you at the top of the graph go back to (0, 3) and go down 4 points and 1 point to the left. repeat. until you reach the bottom. trace the line.
number 12: a bit more tricky. starting point is (0, 5) for this one you go up 6 points and across 5 to the right. repeat. until you get to the top then go back to (0, 5) and go down 6 points and across 5 to the left. repeat. once you reach the bottom trace your line. then done! Sorry to inform you I don't know about 13 and 14! :(
Bonus but still important: the reason why you are going left and right on some of the lines is because the + or - in your equations tell you which direction the line is facing, toward the left (on the top part of your graph) would be - and toward the right part of your would be a + in the equation
More Bonus: a formula Is y=mx + b (0, b)( for ex: 0,5) is the starting point and (mx or for ex 4x is the amount you go up and across. When there is a x that always means across 1 and when there is not a x (ex: 6/5) it's across whatever the 5 is. ex: 6/6 is up 6 and across 6
Hope this helps!
sin−1(sin/6)
cos−1(cos5/4)
tan−1(tan5/6) compute without using a calculator
Answers
Without using a calculator, the trigonometric expressions simplify to:
1. sin^(-1)(sin(θ/6)) = θ/6
2. cos^(-1)(cos(5/4)) = 5/4
3. tan^(-1)(tan(5/6)) = 5/6.
To compute the trigonometric expressions without using a calculator, we can make use of the properties and relationships between trigonometric functions.
1. sin^(-1)(sin(θ/6)):
Since sin^(-1)(sin(x)) = x for -π/2 ≤ x ≤ π/2, we have sin^(-1)(sin(θ/6)) = θ/6.
2. cos^(-1)(cos(5/4)):
Similarly, cos^(-1)(cos(x)) = x for 0 ≤ x ≤ π. Therefore, cos^(-1)(cos(5/4)) = 5/4.
3. tan^(-1)(tan(5/6)):
tan^(-1)(tan(x)) = x for -π/2 < x < π/2. Thus, tan^(-1)(tan(5/6)) = 5/6.
Hence, without using a calculator, we find that:
sin^(-1)(sin(θ/6)) = θ/6,
cos^(-1)(cos(5/4)) = 5/4,
tan^(-1)(tan(5/6)) = 5/6.
To know more about trigonometric expressions refer here:
https://brainly.com/question/12676341#
#SPJ11
Help me with this answer please

Answers
The point that is NOT 5 units away from the point (1,4) is (4,0).
A set of books sits on a shelf at a store. This line plot shows the thickness of each book. Juan buys one of the thickest books on the shelf. Min buys the third thinnest book on the shelf.
How much thicker is Juan’s book than Min’s book?

Answers
Answer: 2 and a half
Step-by-step explanation:
So the thickest book would be value 4 on the line plot. The third thinker would be 2 1/2. When you subtract these two numbers you should get 2 1/2 as the answer. If helped mark me the brainiest!!
find the equations of the tangents to the curve x = 9t2 6, y = 6t3 3 that pass through the point (15, 9). y = (smaller slope) y = (larger slope)
Answers
To find the equations of the tangents to the curve x = 9t^2+6, y = 6t^3+3 that pass through the point (15, 9), we first need to find the points where the tangents touch the curve.
We do this by differentiating both x and y with respect to t and finding the value of t when the slope of the tangent line is equal to the slope of the line passing through (15,9).
Differentiating x and y with respect to t, we get dx/dt = 18t and dy/dt = 18t^2. The slope of the tangent line at a point (x,y) on the curve is given by dy/dx = (dy/dt)/(dx/dt) = t/3.
To find the values of t where the tangent line passes through (15,9), we solve the equation (y-9)/(x-15) = t/3 for t. Substituting x = 9t^2+6 and y = 6t^3+3, we get the quadratic equation 2t^2-3t+1 = 0, which factors as (t-1)(2t-1) = 0. Therefore, the two values of t are t = 1/2 and t = 1.
Now, we find the slopes of the tangent lines at t = 1/2 and t = 1 by substituting these values into the expression for dy/dx. We get slopes of -1/6 and 1/3, respectively. Using the point-slope form of the equation of a line, we can write the equations of the tangent lines as y-9 = (-1/6)(x-15) and y-9 = (1/3)(x-15).
Simplifying, we get y = (-1/6)x + 63/2 and y = (1/3)x + 3/2. Therefore, the equations of the tangents to the curve that pass through the point (15,9) are y = (-1/6)x + 63/2 and y = (1/3)x + 3/2.
Leran more about tangents here: brainly.com/question/10053881.
#SPJ11
Complete the statements below that show y = x2 + 2x - 1 being converted to vertex form.
Form a perfect-square trinomial.
y = x2 + 2x +
− 1−
Answers
We want to complete the steps to convert the given quadratic equation into vertex form.
Eventually we will get:
y = (x + 1)^2 - 2
Vertex form of a quadratic equation.
For a quadratic equation with the vertex (h, k), the vertex form is:
y = a*(x - h)^2 + k
Here we start with:
y = x^2 + 2x - 1
1) First, we complete the perfect-square trinomial, we need to add and subtract 1 to get that:
y = x^2 + 2x - 1 + 1 - 1
2) Now we rewrite the equation to be able of completing squares:
y = (x^2 + 2x + 1) - 1 - 1
y = (x^2 + 2x + 1) - 2
3) Now we complete squares
y = (x + 1)^2 - 2
And this is the equation in vertex form, where you can see that the vertex is the point (-1, - 2)
If you want to learn more about quadratic equations, you can read:
https://brainly.com/question/17177510
A painter charges $15.33 per hour, plus an additional amount for the supplies. If he made $188.18 on a job where he worked 7 hours, how much did the supplies cost?
Answers
This is because 15.33 • 7 = 107.31 and 188.18 - 107.31 = 80.87
What is the domain of the step function f(x) = [2x]- 1?
O {x|x2-1}
O {x|x ≥ 1}
O x x is an integer}
O {x|x is a real number}
Answers
Domain: {x | x is a real number}
Option D, "{x | x is a real number}" accurately represents the domain of the function.
The domain of the step function f(x) = [2x] - 1, where [2x] represents the greatest integer less than or equal to 2x, can be determined by considering the restrictions on the input values.
In this case, the step function is defined for all real numbers. However, the greatest integer function imposes a restriction. Since the greatest integer function only outputs integers, the input values (2x) must be such that they produce integer outputs.
For any real number x, the greatest integer less than or equal to 2x will always be an integer. Therefore, the domain of the function f(x) = [2x] - 1 is:
Domain: {x | x is a real number}
Option D, "{x | x is a real number}" accurately represents the domain of the function.
for such more question on Domain
https://brainly.com/question/16444481
#SPJ8
The following set of data is for the measurement of the mass of Ca in g in a solid sample with an average total mass of 4.3382 ± 0.0054 g.
0.3775, 0.3795, 0.3788, 0.3762, 0.3802
a. Calculate the mean, standard deviation, and relative standard deviation for the mass of Ca in g.
b. Using the average total mass and standard deviation is given, calculate the average percent weight of Ca and standard deviation in the percent weight? You will need to use propagation of error to get the standard deviation of the percent weight Ca. From the average and standard deviation, calculate the RSD and 95% confidence interval of the percent weight Ca also.
Answers
a. The mean mass of Ca in the solid sample is 0.3784 g with a standard deviation of 0.0014 g and a relative standard deviation of 0.37%.
b. The average percent weight of Ca in the solid sample is 8.73% with a standard deviation of 0.32%. The 95% confidence interval for the percent weight of Ca is 8.09% to 9.37%.
To calculate the mean mass of Ca in the solid sample, we sum up the individual measurements and divide by the total number of measurements. Adding the given values, we get a sum of 1.8912 g. Dividing this sum by 5 (the number of measurements) gives us the mean mass of Ca as 0.3784 g.
To calculate the standard deviation, we subtract the mean from each individual measurement, square the differences, sum up the squared differences, divide by the total number of measurements minus 1 (in this case, 4), and take the square root of the result. This gives us a standard deviation of 0.0014 g.
The relative standard deviation (RSD) is calculated by dividing the standard deviation by the mean and multiplying by 100 to express it as a percentage. In this case, the RSD for the mass of Ca is 0.37%.
Learn more about the Standard deviation
brainly.com/question/13498201
#SPJ11
Draw a picture first, then use the Pythagorean Theorem to solve. Round
your answer to the nearest tenth.
A wire is stretched from the top of an 8-ft. pole, to a bracket 5-ft. from the
base of the pole. How long is the wire?
O 9.4
09.0
O 89.0
O 13
Answers
Answer:
your answer would be 9.4
Step-by-step explanation:
you'd have to plug in the numbers in the equation.
8^2 + 5^2 = c^2
64 + 25 = c^2
89 = c^2 then you'd do the square root of 89 which will give you 9.4 when rounded to the nearest tenth.
use the given frequency distribution to find the (a) class width. (b) class midpoints of the first class. (c) class boundaries of the first class.
Answers
(a)The class width = 3
(b) The class midpoint of the first class = 51
(c) The class boundaries of the first class = (49.5, 52.5)
Consider the frequency distribution in the following image.
We know that in frequency distribution the class width is nothing but the distance between the lower limits of consecutive classes.
Whereas the range is the difference between the maximum and minimum data entries.
The smallest number is 50, and the largest is 62.
So the range is 62 - 50 = 12
We know that the formula for the class width:
Class width= upper limit – lower limit +1
So, the class width = 52 - 50 + 1
= 3
The formula for the midpoint of each class:
midpoint = (lower limit of class + upper limit of class)/2
Let us assume that m be the midpoint of the first class.
Using above formula of midpoint:
m = (50 + 52)/2
m = 51
We know that the class boundaries are nothing but the end points of an open interval which contains the class interval.
So, the class boundaries of the first class = (49.5, 52.5)
Learn more about the frequency distribution here:
https://brainly.com/question/14926605
#SPJ4

An online curriculum provider offers their product to two audiences: independent learners (self-directed) and classroom learners (led by their teachers).
They want to understand the differences between the audiences and how they use the product, so they sent surveys and collected data. Users rated their satisfaction with the product from 1-10, where 1 is least satisfied and 10 is the most satisfied.
This scatter plot compares the hours per week spent by a user to their rating of the product:
The green dots represent classroom learners and the purple dots represent independent learners.
Which hypothesis is most consistent with the chart?
Answers
The hypothesis most consistent with the chart is that there is a positive correlation between the hours per week spent using the product and the satisfaction ratings for both classroom learners and independent learners.
Based on the scatter plot comparing the hours per week spent by users to their rating of the product, the hypothesis that seems most consistent with the chart is:
Hypothesis: There is a positive correlation between the hours per week spent using the product and the satisfaction ratings for both classroom learners and independent learners.
Explanation: The scatter plot shows a general trend where higher ratings are associated with higher hours per week spent using the product. Both the green dots representing classroom learners and the purple dots representing independent learners exhibit this pattern. It suggests that as users spend more time engaging with the online curriculum, their satisfaction levels tend to increase.
While there is some variability in the data points, with a few outliers where users have low ratings despite spending more hours, the overall trend indicates a positive correlation. This means that, on average, users who dedicate more time to using the product tend to have higher satisfaction levels. This consistency between the two audiences (classroom learners and independent learners) suggests that the relationship between time spent and satisfaction applies to both groups.
It's important to note that correlation does not necessarily imply causation. Other factors, such as the quality of content, user interface, or individual learning preferences, could also contribute to user satisfaction. However, based on the information presented in the scatter plot, the hypothesis of a positive correlation between hours per week spent and satisfaction ratings appears to be the most consistent explanation.
for such more question on hypothesis
https://brainly.com/question/24029881
#SPJ11
Solve the system by substitution.
y = 9x
y = 3x – 24
Answers
Answer:
-24
Step-by-step explanation:
i dont think this is right answer
hope this helps via substitution process

will someone please figure this out?
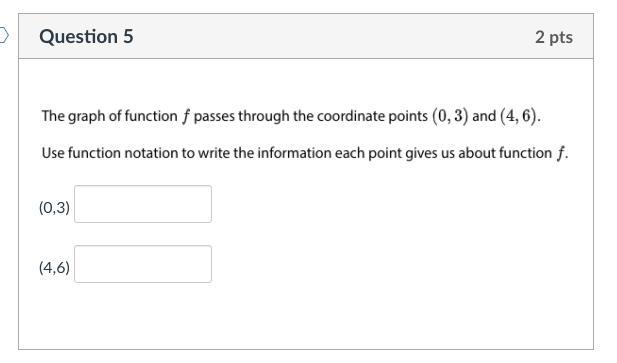
Answers
Answer:
0,3 is point saying that this is not proportional 4 6 continues the fashion of bases by the point of origin which doesnt exisist or 0,0 so that doesnt work
Step-by-step explanation:
pls answert my question too
Expand using the distributive property -2(2 +3x)
Answers
Answer:
-4 - 6x
Step-by-step explanation:
-2 (2 + 3x)
-4 - 6x
-4 - -6x
Explanation:
-2 x 2 = -4
-2 * 3x = -6x
3x+1=4
Solve for x. Correct answer get's brainliest
Answers
Answer:
X=1
Step-by-step explanation:
3x+1=4
3x=3
X=1
why won't anybody help me?



Answers
Answer:
b. -4 an C then A
Step-by-step explanation:
hope this helps!
Answer:
It will be 4
Step-by-step explanation:
i know
if a rock is soft and the color blue is red then my is a car driving a fish then why are my shoes untied?
Answers
Answer:
tuff
Step-by-step explanation:
I would appreciate it if you can help me with this.

Answers
Answer:
\(450000 \leqslant 15000 + 4t\)
The coordinates of the point J are (-1,3) and the coordinates of point K are
(-1,8). What is the distance, in units, between the point J and point K?
Answers
Answer:
1 Step-by-step explanation:
Place the expression that makes the sentence true.
Mark brought $20 to a baseball game. He bought 2 drinks while at the game. Mark set up
an expression to model his situation, where d represents the cost of a drink.
What expression models the amount of money Mark has after the game?
Answers
Answer:
20-2d=x
Step-by-step explanation:
we need the amount that he has so that we could figure the amount each drink cost but this is the answer
select two values of x that are roots of this equation (picture included)
x^2+2x-5=0

Answers
Answer:
B and D
Step-by-step explanation:
i took this test
The roots of the equation will be - 1 - √6 and - 1 + √6. Then the correct options are B and D.
What is the solution to the equation?The distribution of weights to the variables involved that establishes the equilibrium in the calculation is referred to as a result.
The quadratic equation is given below.
x² + 2x - 5 = 0
The solution of the quadratic equation will be
x² + 2x - 5 = 0
Add 1 on both sides, then the equation will be
x² + 2x + 1 - 5 = 1
x² + 2x + 1 = 1 + 5
(x + 1)² = 6
Taking square root on both sides, then the equation will be
x + 1 = ±√6
x = - 1 ±√6
Then the roots of the equation will be - 1 - √6 and - 1 + √6.
Then the correct options are B and D.
More about the solution of the equation link is given below.
https://brainly.com/question/545403
#SPJ5
PLEASE HELP !!
I’m reposting this because no way someone’s gonna find that question so far down

Answers
Answer: The slope of parallel lines are the same
Step-by-step explanation:
There are not triangles in the image, but instead two lines creating a corner, they want you to connect the opposite corners of each of these sets of lines to create a triangle.
The bigger set of lines is up 2 right 8. slope is rise/run so the slope is 2/8 or if we simplify 1/4
The smaller set of lines is 1 up 4 right. slope is rise over run so the slope is 1/4.
The problem tries to confuse you by not connecting those lines and by having the bigger one go up first then right, and then the smaller one go right first and then up.
But as you can see the parallel lines both have a slope of 1/4
the only difference between parallel lines is the 'b' in the equation y=mx+b
what does the coefficient used to assess the internal consistency of a measure represent?
Answers
The coefficient used to assess the internal consistency of a measure typically refers to Cronbach's alpha coefficient.
What does the coefficient used to assess the internal consistency of a measure represent?The coefficient used to assess the internal consistency of a measure typically refers to Cronbach's alpha coefficient. This coefficient is a statistic that quantifies the internal consistency reliability of a scale or measure, specifically for measures with multiple items or indicators that are intended to measure the same underlying construct.
The coefficient ranges between 0 and 1, with higher values indicating greater internal consistency. Cronbach's alpha measures the extent to which the items in a scale or measure correlate with each other. It assesses how well the items are measuring the same underlying construct or concept.
In other words, the coefficient represents the proportion of variance in the observed scores that can be attributed to the true score, rather than measurement error or other extraneous factors. It indicates the degree to which the items in the measure are interrelated or consistent with each other, with higher values suggesting stronger internal consistency.
Researchers often use Cronbach's alpha to assess the reliability of scales in various fields, such as psychology, education, and social sciences, to ensure that the measure is measuring the construct consistently and accurately.
Learn more about coefficient on:
https://brainly.com/question/1038771
#SPJ4
PLZZ HELP FAST
Use the distributive property to fill in the blanks

Answers
Answer:
first blank : 6
second blank : 5
Step-by-step explanation:
Is (3,10) a solution to this system of equations?
y=2x+3
y=x+7
Answers
Answer: no
Step-by-step explanation:
plug in (3,10) to y=2x+3
10=2(3)+3
10=6+3
10\(\neq\)9
which expression is equivalent to (x4)^9
Answers
Answer:
Step-by-step explanation:
\((a^{m})^{n}=a^{m*n}\\\\(x^{4})^{9}=x^{4*9}=x^{36}\)
