Question 1
Fill in the blank question.
The sum of two numbers is 20.5. Their difference is 6.5. Find the two numbers.
Part A
Write a system of equations that represents the situation.
x+y=_____
x−y=_____
Part B
Solve the system of equations. Express the coordinates as decimals if necessary.
( _____, _____)
Part C
Interpret the solution.
The greater number is
____________________
and the lesser number is
____________________
Answers
Answer:
x = 13.5
y = 7
(13.5,7)
what the solution means is that (13.5,7) would be the point at which the two lines, x+y=20.5 and x-y=6.5, would intersect
Step-by-step explanation:
x + y = 20.5
x - y = 6.5
if we add the two equations we get:
2x = 27
x = 13.5
y = 20.5 - 13.5
y = 7
solution as an ordered pair:
(13.5,7)
What the solution means is that (13.5,7) would be the point at which the two lines, x+y=20.5 and x-y=6.5, would intersect
Related Questions
Solve the given differential equation x^3 y"' - 6y = 0 y(x) = ______ , x > 0
Answers
The solution to the given differential equation is:
\(\[y(x)\ =\ a_0 + a_1x + \frac{1}{4}a_1x^4 + \sum_{n=2}^{\infty} \frac{2a_{n-2}}{(n-2)(n-1)}x^{n+3}\]\)
How did we get the value?To solve the given differential equation
\(x^3y'''\ -\ 6y\ =\ 0,\)
we can use the method of power series. Let's assume a power series solution of the form
\(y(x)\ =\ \sum_{n=0}^{\infty} a_nx^n.\)
Differentiating y(x) with respect to x gives:
\(\[y'(x)\ =\ \sum_{n=0}^{\infty} n a_n x^{n-1}\ =\ \sum_{n=0}^{\infty} (n+1) a_{n+1} x^n\]\)
Differentiating again gives:
\(\[y''(x)\ =\ \sum_{n=0}^{\infty} (n+1)na_{n+1}x^{n-1}\ =\ \sum_{n=0}^{\infty} (n+2)(n+1)a_{n+2}x^n\]\)
Differentiating one more time gives:
\(\[y'''(x)\ =\ \sum_{n=0}^{\infty} (n+2)(n+1)na_{n+2}x^{n-1}\ =\ \sum_{n=0}^{\infty} (n+3)(n+2)(n+1)a_{n+3}x^n\]\)
Substituting these expressions into the differential equation, we have:
\(\[x^3 \sum_{n=0}^{\infty} (n+3)(n+2)(n+1)a_{n+3}x^n - 6 \sum_{n=0}^{\infty} a_n x^n\ =\ 0\]\)
Rearranging the terms and combining like powers of x, we get:
\(\[\sum_{n=0}^{\infty} (n+3)(n+2)(n+1)a_{n+3}x^{n+3} - 6 \sum_{n=0}^{\infty} a_n x^n\ =\ 0\]\)
Now, let's equate the coefficients of like powers of x to zero:
For n=0:
\(\[(3)(2)(1)a_3 - 6a_0 = 0 \implies 6a_3 - 6a_0 = 0 \implies a_3 = a_0\]\)
For n=1:
\(\[(4)(3)(2)a_4 - 6a_1 = 0 \implies 24a_4 - 6a_1 = 0 \implies a_4 = \frac{1}{4}a_1\]\)
\(For \: n\geq 2:
\[(n+3)(n+2)(n+1)a_{n+3} - 6a_n = 0 \implies a_{n+3} = \frac{6a_n}{(n+3)(n+2)(n+1)}\]
\)
Now we can write the solution as:
\(\[y(x)\ =\ a_0 + a_1x + \frac{1}{4}a_1x^4 + \sum_{n=2}^{\infty} \frac{6a_{n-2}}{n(n-1)(n-2)}x^{n+3}\]
\)
Simplifying the series, we get:
\(\[y(x)\ =\ a_0 + a_1x + \frac{1}{4}a_
1x^4 + \sum_{n=2}^{\infty} \frac{2a_{n-2}}{(n-2)(n-1)}x^{n+3}\]
\)
Therefore, the solution to the given differential equation is:
\(\[y(x)\ =\ a_0 + a_1x + \frac{1}{4}a_1x^4 + \sum_{n=2}^{\infty} \frac{2a_{n-2}}{(n-2)(n-1)}x^{n+3}\]\)
where a₀ and a₁ are arbitrary constants to be determined based on the initial conditions or boundary conditions given in the problem.
learn more about differential equation: https://brainly.com/question/1164377
#SPJ1
\( {75}^{2} + 25 - 750\)
Answers
Point b is located at (-6,-6). on a coordinate grid. point b is translated 5 units up and 12 units to the right to create b prime.. what is the distance between point b and point b prime. in units?
Answers
The distance between point B and point B prime is 13 units.
Distance Formula: Let (x₁, y₁) and (x₂, y₂) be two points in the coordinate plane.
Then the distance between these points is given by the formula:
d = √[(x₂ − x₁)² + (y₂ − y₁)²]
So, let's begin by finding the coordinates of point B prime.
Since point B is translated 5 units up and 12 units to the right to create B prime, the coordinates of B prime are:
(x,y)(x,y)=(−6+12,−6+5)=(6,-1)
Using the distance formula to find the distance between the points, we have:
d = √[(x₂ − x₁)² + (y₂ − y₁)²]d
= √[(6 − (-6))² + ((-1) − (-6))²]d
= √[(6 + 6)² + (5)²]d
= √[12² + 5²]d
= √(144 + 25)d
= √169d
= 13
Learn more about Distance Formula from :
https://brainly.com/question/661229
#SPJ11
He regular hexagon has a radius of 4 in. A regular hexagon has a radius of 4 inches. What is the approximate area of the hexagon? 24 in.2 42 in.2 48 in.2 84 in.2
Answers
Answer:
41.57 in²
Step-by-step explanation:
Answer:
41.57 in² round it up and it's 42
Step-by-step explanation:
I just did it
Brainliest pls
i performed a hypothesis test, and my p-value cutoff (significance level) was 1%. what's the chance that my test will incorrectly reject the null hypothesis? a. 1% b. 95% c. 99% d. not enough information to determine e. 5%
Answers
The chance that a hypothesis test will incorrectly reject the null hypothesis when the p-value cutoff is 1%. The correct option is A.
What is a hypothesis test?A hypothesis test is used to test the validity of a hypothesis by calculating the probability that a sample statistic occurred by chance.
The null hypothesis is the hypothesis that is being tested, and it is usually assumed to be true unless there is evidence to the contrary.
The p-value is the probability of obtaining a sample statistic at least as extreme as the one observed, assuming the null hypothesis is true. If the p-value is less than the significance level, which is the p-value cutoff chosen by the researcher, then the null hypothesis is rejected.
If the p-value is greater than or equal to the significance level, then the null hypothesis is not rejected. The p-value cutoff is the significance level chosen by the researcher, and it represents the maximum probability of rejecting the null hypothesis when it is actually true.
In this case, the p-value cutoff is 1%, which means that the maximum probability of rejecting the null hypothesis when it is actually true is 1%. Therefore, the chance that a hypothesis test will incorrectly reject the null hypothesis when the p-value cutoff is 1%.
Therefore, the correct option is A.
Learn more about hypothesis test here:
https://brainly.com/question/30588452
#SPJ11
What are the coordinates of point B on AC such that the ratio of AB to AC is 5:6
Answers
Coordinates of point B are (5x₂+6x₁)/11 and (5y₂+6y₁)/11
What is the section formula in coordinate geometry?
When the line segment is divided internally in the ratio m:n, we use this formula. That is when point C lies somewhere between points A and B. p= (mx₂+nx₁)/(m+n) & q= (my₂+ny₁)/(m+n)
Given here, point B on AC such that the ratio of AB to AC is 5:6
Let the point B(p,q) internally divide the line joining points A(x₁, y₁) and C(x₂, y₂) in the ratio m : n , then,
p= (mx₂+nx₁)/(m+n)
q= (my₂+ny₁)/(m+n)
Here. m=5 and n=6
p=(5x₂+6x₁)/11 , q=(5y₂+6y₁)/11
Hence, the Coordinates of point B are (5x₂+6x₁)/11 and (5y₂+6y₁)/11
I hope this helps <3
find a value of c so that p(z ≥ c) = 0.55.
Answers
To find a value of c such that P(z ≥ c) = 0.55, we need to use a standard normal distribution table or calculator.From the standard normal distribution table, we find that the z-score corresponding to a right-tailed area of 0.55 is approximately 0.126.
Therefore, we have:
P(z ≥ c) = 0.55
P(z ≤ c) = 1 - P(z ≥ c) = 1 - 0.55 = 0.45
Using the standard normal distribution table, we find that the z-score corresponding to a left-tailed area of 0.45 is approximately -0.126.
So, c = -0.126.
Therefore, the value of c that satisfies P(z ≥ c) = 0.55 is approximately -0.126.
To learn more about distribution : brainly.com/question/29664127
#SPJ11
What is the value of the expression 144−−−√243−−−√5−5+16÷64−−√3?
Answers
Answer: 150.95
Step-by-step explanation:144 -\(\sqrt{243}\) -\(\sqrt{5}\) -5 +16 /64 -\(\sqrt{3}\)
144-5+16/64=139+0.25
=139.25 or 139,1,4
\(\sqrt{243} -\sqrt{5} -\sqrt{3}\) =15.6-2.2-1.7
=11.7
added together
11.7+139.25=150.95
Graph equation using the slope and Y intercept
Y= -2X +2

Answers
Answer:
Step-by-step explanation:
slope=-2
y-intercept=(0,2)

45% of 30 is equal to 18% of what number
Answers
Answer:
75
Step-by-step explanation:
(0.45)(30) = (0.18)x
x = (0.45)(30) / (0.18)
x = 13.5 / 0.18 = 75
Check the answer:
(0.45)(30) = (0.18)(75)
13.5 = 13.5 answer is correct!
Answer:
Step-by-step explanation:
45% of 30 = 18% of some number
In this kind of questions, we usually assume the missing number as as something
Let the number be x
So assuming the number is x, the equation will be as follows:
45% of 30 is equal to 18% of x
45/ 100 * 30 = 18/100 * x
This means that 0.45 *30= 0.18 * x
Therefore, 13.5 = 0.18 x
Thus X = 13.5 / 0.18
Which is equal to 75
Thus 45% of 30 is equal to 18% of 75
Proving the above situation as follows:
45% OF 30 = 13.5
And 18% of 75 = 13.5
Thus both equations are equal.
Solution =75
two players, a and b, alternatively toss a fair coin (a tosses the coin first, then b tosses the coin, then a , then b .. .). the sequence o f heads and tails is recorded. i f there is a head followed by a tail (ht subsequence), the game ends and the person who tosses the tail wins. what is the probability that a wins the game?
Answers
When two players A and B alternately flip a fair coin, the probability E(T) is 4. (A tosses the coin first, then B tosses the coin, then A, then B and so on).
What is probability?Probability theory, a subfield of mathematics, gauges the likelihood of an occurrence or a claim being true. An event's probability is a number between 0 and 1, where approximately 0 indicates how unlikely the event is to occur and 1 indicates certainty.
Two players, A and B, turn a fair coin in succession (A tosses the coin first, then B tosses the coin, then A, then B and so on). The order of the heads and tails is noted. If there is a head followed by a tail, the game is done, and the person who throws the tail wins (HT sub-sequence).
We must ascertain the game's estimated duration. Allow T coin tosses for the game to proceed. Find E (T).
\(E(T) = first instance of HT in seriesE(T) =0.5×(1+2)+0.5×(1+E(T))\\0.5×E(T)=0.5×4\\E(T) =4\)
As a result, when two players A and B alternately flip a fair coin, The E(T) is 4. (A tosses the coin first, then B tosses the coin, then A, then B and so on).
To know more about probability visit:
https://brainly.com/question/11234923
#SPJ4
If X1,X2, Xn constitute a random sample from population with the mean μ, what condition must be imposed on the constants a1, a2,.......,an so that a1X1 + a2X2 +.....+ anXn is an unbiased estimator of μ?
Answers
The condition imposed such that a₁X₁ + a₂X₂ +.....+ aₙXₙ is an unbiased estimator of μ must be that ∑a = 1
We are given that X₁, X₂, ... Xₙ constitute a random sample from the population with the mean μ.
This implies, E(X) = μ
Now we have another set of data here, a₁X₁ + a₂X₂ +.....+ aₙXₙ
For a₁X₁ + a₂X₂ +.....+ aₙXₙ to be an unbiased estimator of μ, we should have
E(∑aX) = μ
or, ∑a E(X) = μ
Now we already know that
E(X) = μ
Hence we get
∑a = 1
Hence condition imposed must be that ∑a = 1
To learn more about Estimation visit
https://brainly.com/question/14368422
#SPJ4
Correct Question
If X₁, X₂, ... Xₙ constitute a random sample from the population with the mean μ, what condition must be imposed on the constants a₁, a₂, ... aₙ so that a₁X₁ + a₂X₂ +.....+ aₙXₙ is an unbiased estimator of μ?
Can someone Help me on #9

Answers
Answer:
See Below
Step-by-step explanation:
If DF = 42, What is DE?
D__________E_______F
(7x + 1) + ( 4x-3) = 42
7x+1+ 4x -3 = 42 Solve for x
11x -2 = 42
+2 +2
11x = 44
11x / 11 = 44/ 11
x = 4
Now plug x in for the equation of DE
7x+1
7(4) + 1
28 + 1 = 29
DE = 19
number that results from multiplying two or more numbers
Answers
Answer:
This is called the product.
Step-by-step explanation:
Answer:
The result of a multiplication operation is called a product. The multiplication of whole numbers may be thought of as a repeated addition; that is, the multiplication of two numbers is equivalent to adding as many copies of one of them, the multiplicand, as the quantity of the other one, the multiplier.
Step-by-step explanation:
AB||CD . Find the value of x.
A. 25
B. 45
C. 15
D. 10

Answers
Answer:
The value of x is 10.
3x+15=5x-5
3x=5x-5-15
3x=5x-20
3x-5x=(-20)
(-2x)=(-20)
x=10
Select the correct answer from each drop down menu. In the figure, AB=__inches and AC=___
10" inches

Answers
Answer: In the figure AB is about 8.4 inches and AC is about 13.05 inches.
Step-by-step explanation: We can use cosine to find the hypotenuse. \(cos(40)=\frac{10}{x} \\cos(40) (x)=\frac{10}{x}(x)\\cos(40) (x) =10\\\frac{cos(40) (x)}{cos (40)} =\frac{10}{cos (40)} \\x=\frac{10}{cos(40)}\)
Using a calculator x is about 13.05
Using tangent we can find the length opposite of <C
\(tan(40)=\frac{x}{10} \\tan(40) (10)=\frac{x}{10}(10)\\tan(40) (10) = x\)
Using a calculator x would be about 8.4
Answer:
Step-by-step explanation:

7 minus the quotient of 6 and v
Answers
Answer:
(\(\frac{6}{v}\)) - 7
Step-by-step explanation:
7 minus the quotient of 6 and v
\/
(\(\frac{6}{v}\)), 7 minus
\/
(\(\frac{6}{v}\)) - 7
Have a nice day!
If this is not what you are looking for - comment! I will edit and update my answer accordingly. (ノ^∇^)
- Heather
The ratio of oranges sold to bananas sold is 3 to 10. If a total of 30 bananas were sold,then how many oranges were sold ?
Answers
Answer:
9
Each value is 3 times the number on the ratio.
10 x 3 = 30.
So, the ratio for oranges would be 9 because:
3 x 3 = 9.
So, the answer is 9.
please solve this question
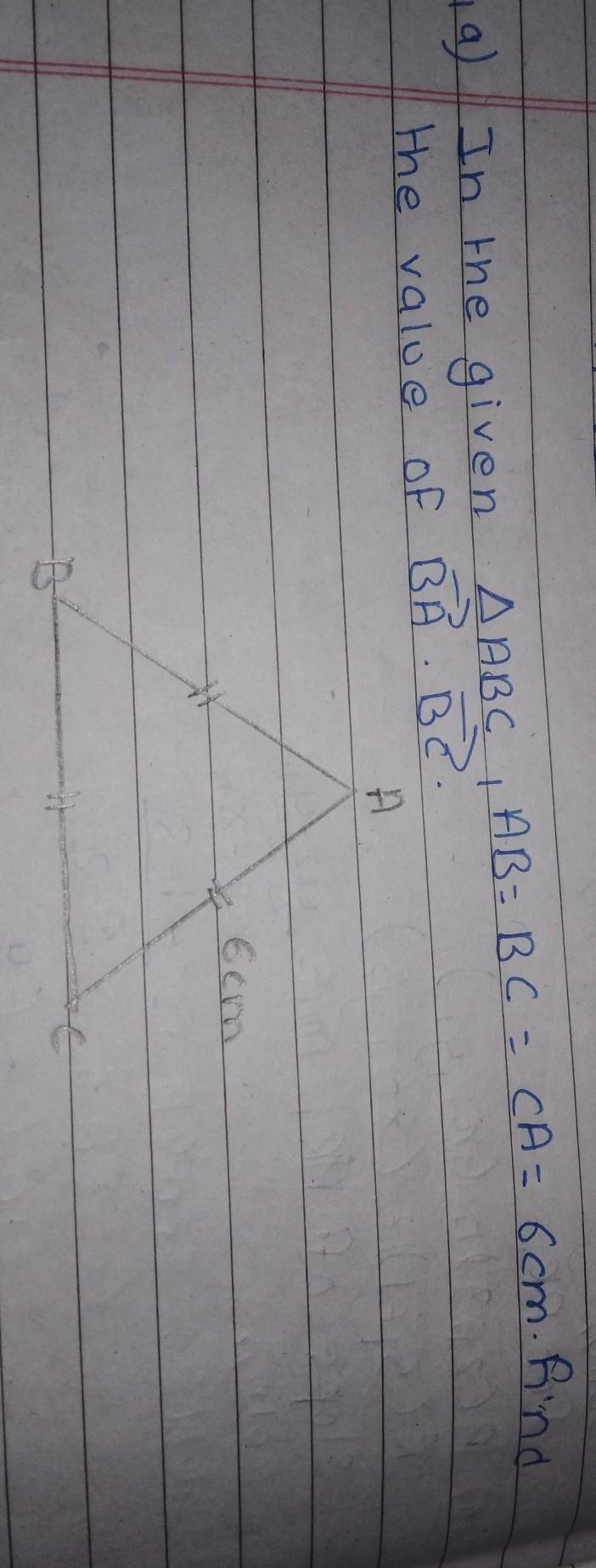
Answers
The value of BA.BC vector is 18 cm² as side lengths are 6 cm.
What is triangle?A triangle is a closed two-dimensional geometric figure with three sides, three angles, and three vertices. It is one of the basic shapes in geometry and is formed by connecting three non-collinear points with straight line segments. The sum of the interior angles of a triangle is always 180 degrees, and there are various types of triangles, such as equilateral, isosceles, scalene, right-angled, acute-angled, and obtuse-angled triangles. Triangles are used in a wide range of applications, from architecture and engineering to physics and computer graphics.
Here,
To find the area of the AABC, we can use Heron's formula:
s = (AB + BC + CA)/2 = (6 + 6 + 6)/2 = 9
Area = √(s(s-AB)(s-BC)(s-CA))
= √(9(9-6)(9-6)(9-6))
= 27/4 cm²
To find the height of the AABC corresponding to side AB, we can use the formula:
Area = 1/2 * AB * height
Rearranging, we get:
height = 2 * Area / AB = 2 * 27/4 / 6 = 9/4 cm
Therefore, the area of AABC is 27/4 cm², and the height corresponding to side AB is 9/4 cm.
For the second part of the question, we can use the Law of Cosines to find the angle between sides BA and BC:
cos(A) = (BA² + BC² - CA²) / (2 * BA * BC)
= (6² + 6² - 6²) / (2 * 6 * 6)
= 1/2
A = arccos(1/2) = 60 degrees
Using this angle, we can find the length of side BA . BC:
BA . BC = 2 * AB * BC * cos(A)
= 2 * 6 * 6 * cos(60)
= 18 cm²
Therefore, BA . BC = 18 cm²
To know more about triangle,
https://brainly.com/question/28600396
#SPJ1
The point (–5, –9) was reflected over an axis to become the point (5, –9). Which axis was it reflected over? Explain.
x-axis, because the x-coordinate is the opposite
x-axis, because the y-coordinate is the opposite
y-axis, because the x-coordinate is the opposite
y-axis, because the y-coordinate is the opposite
Answers
The point (-5, -9) was reflected over the y-axis to become the point (5, -9). The x-coordinate changed sign the y-coordinate remained the same, confirming that the reflection took place over the y-axis.
The point (-5, -9) was reflected over the y-axis to become the point (5, -9).
To understand which axis the reflection occurred over, we need to analyze the changes in the coordinates.
In a reflection over the x-axis, the y-coordinate of a point changes sign while the x-coordinate remains the same.
Similarly, in a reflection over the y-axis, the x-coordinate changes sign while the y-coordinate remains the same.
The y-coordinate of the point (-5, -9) remains the same as -9 in both the original and reflected points.
The x-coordinate changes from -5 to 5.
This means that the reflection involved a change in the x-coordinate, indicating that it occurred over the y-axis.
For similar questions on reflected
https://brainly.com/question/26642069
#SPJ11
Please please help me

Answers
Answer:
The perimeter of the figure will be 62.8 or B
Step-by-step explanation:
1) The radius is 10
2) Perimeter basically means circumference
3) The formula for circumference is 2πr
4) 2π*10
5)2*pi=6.28*10=62.8
a street light is mounted at the top of a 19 foot-tall pole. a 6 foot tall man walks away from the pole at a speed of 5 feet per second along a straight path. how fast is the length of his shadow changing at the instant when he is 24 feet from the pole?
Answers
His shadow changing at the instant when he is 24 feet from the pole Is \(\frac{95}{13}\)
What do triangles that are similar mean?
The related angle measurements and proportional side lengths of similar triangles are the same.
In this diagram, x represents the distance between the man and the pole, while y represents the distance between the shadow's tip and the pole. My assumption is that the man and the pole are both standing straight up, making the two triangles comparable.
by comparison, \(\frac{y-x}{y} = \frac{6}{19}\)
\(19(y-x)=6(y)\\19y-19x=6y\\19y-6y=19x\\13y=19x\\y=\frac{19}{13} y\)
differentiate both sides with respect to t or time.
\(\frac{dy}{dt}=\frac{19}{13}\frac{dx}{dt}\)
You know \(\frac{dx}{dt}\) = 5 ft/s because the man is edging away from the pole at that pace. Find out \(\frac{dy}{dt}\) how quickly the shadow's tip is moving.
That Means, \(\frac{dy}{dt}= \frac{19}{13} * 5 = \frac{95}{13}\)ft/s
Actually, it doesn't matter how far the man is from the pole because only his speed impacts how quickly his shadow moves.
Learn More about similar triangles
https://brainly.com/question/1799826
#SPJ4
Round the number 817.0863 to the nearest:
(a) hundreds
(b) hundredths
(C) 3.d.p
(d) 4 s.f
(e) Whole number
Answers
Answer:
(a) hundreds = 817
(b) hundredths = 817.09
(c) 3 d.p = 817.086
(d) 4 s.f. = 817.1
(e) whole number = 817
serena leans a 24-foot ladder against a 22.8-foot-tall building to climb on the roof.
Answers
Serena leans a 24-foot ladder against a 22.8-foot-tall building to climb on the roof is 71.8 degree.
Measurement of Angle:
The measurement of angles is done using basic geometric tools such as protractors and compasses. This tool helps to find precise measurements of angles. A protractor helps provide accurate measurements of angles, while compasses help construct angles. Angles are measured in three ways: degrees, radians, and revolutions.
According to the Question:
Suppose the measure of angle is θ, then we have
Sinθ = 22.8/24
⇒ Sinθ = 0.95
Therefore,
θ = Sin⁻¹ (0.95)
= 71.8 degree.
Therefore, Serena leans a 24-foot ladder against a 22.8-foot-tall building to climb on the roof is 71.8 degree.
Learn more about Degree:
https://brainly.com/question/364572
#SPJ4
A polygon has vertices at (-1, 3), (−1, 6), (2, 10), (5, 6), and (5, 3).
What is the area of the polygon? Enter your answer in the box.
Answers
The perimeter of the polygon is 22 units.
What is the area of the polygon?
The area of a polygon is defined as the area enclosed by the polygon's boundary. In other words, the region occupied by any polygon determines its area. In this lesson, we will learn how to calculate polygon area and the difference between polygon perimeter and area in detail.
we know that
the perimeter of a polygon is the sum of the length sides
in this problem, we have five vertices
so the polygon has five sides
Let,
A(-1, 3)
B(−1, 6)
C(2, 10)
D(5, 6)
E(5, 3).
the perimeter is equal to
P = AB + BC + CD + DE + AE
The formula to calculate the distance between two points is equal to
d = √(y₂ - y₁)² + (x₂ - x₁)²
The distance of AB:
A(-1, 3)
B(−1, 6)
d = √(6 - 3)² + (-1 - (-1))²
d = √(3)² + (0)²
d = 3
The distance of BC:
B(−1, 6)
C(2, 10)
d = √(10 - 6)² + (2 - (-1))²
d = √(4)² + (3)²
d = 5
The distance of CD:
C(2, 10)
D(5, 6)
d = √(6 - 10)² + (5 - 2)²
d = 5
The distance of DE:
D(5, 6)
E(5, 3).
d = √(3 - 6)² + (5 - 5)²
d = 3
The distance of AE:
A(-1, 3)
E(5, 3)
d = √(3 - 3)² + (5 - (-1))²
d = 6
Find the perimeter
the perimeter is equal to
P = AB + BC + CD + DE + AE
P = 3+5+5+3+6
P = 22 units.
Hence, the perimeter of the polygon is 22 units.
To learn more about the area of the polygon visit,
https://brainly.com/question/22640000
#SPJ1
What is the nth term for 2 3 5 13
Answers
this is a number is can not devide

Find the derivative, if it exists, of the function at the specified point.() = ^2 − 4 + 3 at = 1
Answers
Find the derivate of the expression using the general procedure to find the derivative of a polynomial function. To do it, multiply the term times the exponent of the variable and raise the variable to the original exponent minus 1:
\(\begin{gathered} f(x)=x^2-4x+3 \\ f^{\prime}(x)=2x^{2-1}-4x^{1-1}-0\cdot3 \\ f^{\prime}(x)=2x-4 \end{gathered}\)Now that we have the expression for the derivative of the function, evaluate it at the value of x that is in the question statement, which is 1:
\(f^{\prime}(1)=2(1)-4=2-4=-2\)The derivative of the function is -2 at x=1.
EASY QUESTION GIVING BRAINLY IF RIGHT.
suppose a real estate agent received 5% commision on the first 200 000$ of a houses selling price and a 6% remaining amount.
a. if the house sells for 345 000$ how much commision does the real estate agent make on the sale of a house?
Answers
Answer:Total Commission
$12
Commission for Each Agent
$6.00
Total Amount Seller Receives
$188
Step-by-step explanation:
Write the expression as a decimal number.
5×10+6×1+1×0.1+1×0.01+8×0.001=
Answers
Answer: 56.118
Step-by-step explanation:
Determine 5% of 300 expressing the percent as a fraction. -Express 5% as 5 100 = 1 20 . -Determine 1 20 of 300.
Answers
300/4 ÷ 4/4 [Divide the numerator and denominator by 4] = 75%. Answer: 75% (ii) Express 12/5 as a percent. Solution: 12/5 × 100 = (12 × 100)/5 = 1200/5