. Seiji and Gavin both worked hard over the summer. Together they earned a total of $425. Gavin earned $25more than Seiji.
(a) Write a system of equations for the situation. Use s for the amount Seiji earned and g for the amount
Gavin earned.
(b) Graph the equations in the system.
(c) Use your graph to estimate how much each person earned.
I need help with b
Answers
Answer: b
Step-by-step explanation:
Its not right im doing this for point
Related Questions
A person who is 6.1 feet tall is standing in a pool. The top of the person's head is 1.8 feet above the surface of the water. How deep is the pool? Write your answer as a decimal.
Answers
D = 6.1 - 1.8 = 4.3 feet
Graph the line with the equation
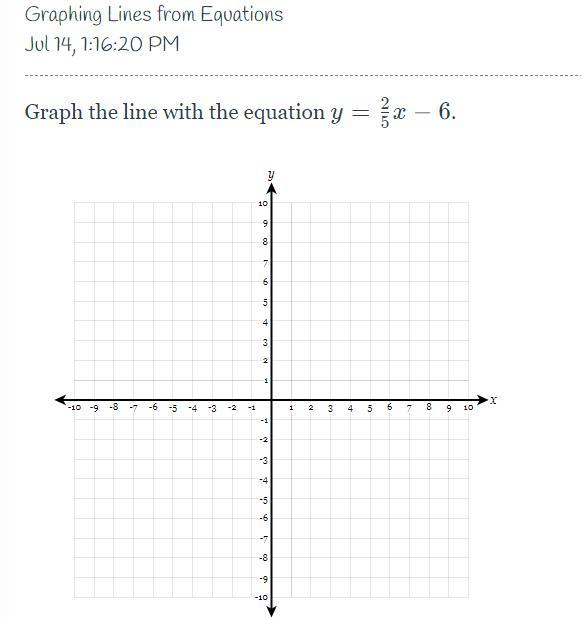
Answers
The graph of the linear equation can be seen in the image below.
How to graph the linear equation?Here we have the linear equation:
y = (2/5)*x - 6
To graph it, we just need to find two points on the line, and then connect them with a line.
To find the points we just evaluate in two values of x.
if x = 0.
y = (2/5)*0 - 6 = -6
Then we have the point (0, -6)
If x = 5.
y = (2/5)*5 - 6 = 2 - 6 = -4
Then we have the point (5, - 4)
Now we can graph these two points and connect them with a line. The graph of the line can be seen below.
If you want to learn more about linear equations:
https://brainly.com/question/1884491
#SPJ1

Solve for m. 4 = 20m Simplify your answer as much as possible.
Answers
Answer:
0.2
Step-by-step explanation:
Let S be the part of the plane 3x+2y+z=3 which lies in the first octant, oriented upward. Find the flux of the vector field F=4i+4j+1k across the surface S.
Answers
The flux of the vector-field F = 4i + 4j + 1k across the surface S is 63/4. We find out the flux of the vector-field using Green's Theorem.
Define Green's Theorem.Flux form of Green's Theorem for the given vector-field
φ = ∫ F.n ds
= ∫∫ F. divG.dA
Here G is equivalent to the part of the plane = 3x+2y+z = 3.
and given F = 4i + 4j + 1k
divG = div(3x+2y+z = 3) = 3i + 2j + k
Flux = ∫(4i + 4j + 1k) (3i + 2j + k) dA
φ = ∫ (12 + 8 + 1)dA
= 21∫dA
A = 1/2 XY (on the given x-y plane)
3x+2y =3
at x = 0, y = 3/2
y = 0, x = 1
1/2 (1*3/2) = 3/4
Therefore flux = 21*3/4 = 63/4
φ = 63/4.
To know more about Green's theorem visit:
https://brainly.com/question/27549150
#SPJ4
a newsletter publisher believes that less than 65% 65 % of their readers own a personal computer. for marketing purposes, a potential advertiser wants to confirm this claim. after performing a test at the 0.02 0.02 level of significance, the advertiser decides to reject the null hypothesis. what is the conclusion regarding the publisher's claim?
Answers
The conclusion regarding the publisher's claim is that it is incorrect if the potential advertiser rejects the null hypothesis. A newsletter publisher believes that less than 65% 65 % of their readers own a personal computer. For marketing purposes, a potential advertiser wants to confirm this claim. After performing a test at the 0.02 0.02 level of significance, the advertiser decides to reject the null hypothesis.
What is a null hypothesis?
The null hypothesis is a fundamental idea in inferential statistics that represents the null assumption. It's frequently utilized to compare datasets and decide whether any differences between them are real or just by chance.
It is also called H0. It is the default theory that no difference exists between two tested populations or data sets.
A hypothesis test is a way of deciding whether the data supports or disproves the null hypothesis. If the null hypothesis is incorrect, it is referred to as a Type I error. If it is true and the data leads to its rejection, it is known as a Type II error.
Thus, after performing the test at the 0.02 level of significance, if the potential advertiser decides to reject the null hypothesis, the publisher's claim is incorrect.
for such more question on publisher's claim
https://brainly.com/question/28159262
#SPJ11
Refer to pictures above real help please

Answers
Answer:
38.7°
Step-by-step explanation:
∆ = Tan-1(opposite/ Adjacent)
=Tan-1(8/10)
= 38.66°
= 38.7° to n nearest tenth
0.18 as a fraction simplest form
Answers
Answer:
9/50
Step-by-step explanation:
First, convert the decimal into a fraction. In this case, convert .18 to 18/100. Find a common factor between the numerator and denominator, which in this case, would be 2. Divide both the numerator and denominator by 2 to get 9/50. 9/50 can't be simplified further, so this is your answer.
Answer:
\(\frac{9}{50}\)
Step-by-step explanation:
0.18 is \(\frac{18}{100}\).
Let's simplify the fraction:
\(\frac{18}{100}= \frac{18/2}{100/2}=\boxed{\frac{9}{50}}\)
Hope this helps.
Consider regular pentagons with side length s, area a, and perimeter p. Suppose f, g, h, and j are functions such that:
f(s) represents the perimeter (in cm) of a regular pentagon whose side length is s cm.
g(p) represents the side length (in cm) of a regular pentagon whose perimeter is p cm.
h(s) represents the area (in cm2) of a regular pentagon whose side length is s cm.
j(a) represents the side length (in cm) of a regular pentagon whose area is a cm2.
Use function notation (with the appropriate functions above) to represent the area of a regular pentagon whose perimeter is 133 cm.
Use function notation (with the appropriate functions above) to represent the perimeter of a regular pentagon whose area is 6.38 cm2.
Which of the following make sense in context? Select all that apply.
g(f(s))
j(h(s))
f(j(a))
f(h(s))
Answers
f(j(a)) make sense in the context.
f(s) represents the perimeter of the pentagon (in cm) whose side length is s cm. (Given) (1)
g(p) represents the side length (in cm) of a regular pentagon whose perimeter is p cm. (Given) (2)
h(s) represents the area (in cm2) of s regular pentagon whose side length is s cm. (Given) (3)
j(a) represents the side length (in cm) of a regular pentagon whose area is a cm2. (Given) (4)
a. Perimeter = 133 cm (given)
Side length of the regular pentagon whose perimeter is 133 cm=g(133) (using 2) (5)
Area of the regular pentagon whose side length is g(133)=h{g(133)} (using 3)
b. Area = 6.38 cm2 (given)
Side length of the regular pentagon whose area is 6.38 cm2=j(6.38) (using 4)
Perimeter of the regular pentagon whose side length is j(6.38)=f{j(6.38)} (using 1)
Hence the answer is f(j(a)) make sense in the context.
To learn more about the pentagons click here https://brainly.com/question/1419173
#SPJ4
need help all information is in the picture. thanks!

Answers
It could be the second one but u also have to consider it could be the last one so now u just choose one but (-3,-3) has no solution so that could help answering it too
PLS HELP ME ON THIS QUESTION I WILL MARK YOU AS BRAINLIEST IF YOU KNOW THE ANSWER!!
Find the interquartile range of the data set that consists of 3, 11, 4, 3, 10, 6, 4, 5.
A. 3.5
B. 5.75
C. 4.5
D. 8
Answers
Answer:
I am thinking it's c
I am not sure
Answer:
25th Percentile: 3.5
50th Percentile: 4.5
75th Percentile: 8
= Interquartile Range: 4.5
I think it shows it's '4.5'.
C
A recursive rule for a geometric sequence is
a1 = 9; an = 2/3 (an−1)
What is the iterative rule for this sequence?
A.) an = 9 • (2/3)^n
B.) an = 2/3 • 9^n
C.) an = 9 • (2/3)^n-1
Answers
Answer:
C. \(a_n=(9)(\frac{2}{3})^{n-1}\)
Step-by-step explanation:
Iterative geometric sequence:
\(a_n=a_1x^{n-1}\)
Recursive geometric sequence:
\(a_n=xa_{n-1}\)
The equations are very similar and you only really need to rearrange it. The factor (2/3) and the first term (9) are given, so you can write the iterative equation:
\(a_n=(9)(\frac{2}{3})^{n-1}\)
And so the answer is C.
find the area if the figure

Answers
Answer:
Hey!
To find the square...
14 x 14 = 196
To find the area of the semicircle...
A = pi x radius ^2 / 2
= 76.969
Step-by-step explanation:
196 + 76.969 = 272.969m^2
ROUND THIS UP TO THE REQUIRED DECIMAL PLACE
You can put 273...
HOPE THIS HELPS!!
Answer:
272.93m^2
Step-by-step explanation:
14*14=196m^2
(3.14*7^2)/2=76.93m^2
196+76.93=272.93m^2
(problem is in picture)

Answers
Answer: A
Step-by-step explanation: since X>y and y>z
HELPPPPPPPPPPPPPPPPPPPPPP

Answers
Answer:
The answer would be team D as their range is 24.
Step-by-step explanation:
Team A: range of 27
Team B: Range of 32
Team C: Range of 27
Team D: Range of 24
Team D has the lowest range found by subtracting the larger number 46 by the smaller number 22.
a. 1.3
b. 9.6
c. 13
d. 1

Answers
Answer: I believe the answer would be 1.3
HOWEVER, if you do have to round to the nearest tenth then the answer would be 1
Step-by-step explanation:
2x+7 = 12x - 6
(subtract 2x from both sides)
7 = 10x - 6
(add 6 to both sides)
13 = 10x
(divide 13/10)
1.3 = x
Solve
−2(x+8)+6=7(x−3) for x algebraically. If your answer is a fraction, write it in reduced, fractional form. Do NOT convert the answer to a decimal.
Answers
Answer:
x = 11/5
Step-by-step explanation:
-2x - 16 + 6 = 7x - 21
5x - 21 = -10
5x = 11
x = 11/5
Answer:
x = 11/9
Step-by-step explanation:
-2(x + 8 ) + 6 = 7(x - 3) {Use distributive property: a(b +c)= a*b +a*c) }
-2x + 8*(-2) + 6 = 7*x - 3*7
-2x - 16 +6 = 7x - 21 {add 2x to both sides}
-10 = 7x + 2x - 21
-10 = 9x - 21 {add 21 to both sides}
-10 + 21 = 9x
11 = 9x {divide both sides by 9)
11/9 = x
a is subset of b. b must include everything a has and at least one additional element. how many ways can a and b have subsets?
Answers
The number of ways that A and B can have subsets is the product of the number of subsets of A and the number of subsets of B, or (2^n) * (2^m) = 2^(n+m).
Subset Ways CalculationA set is a collection of distinct objects, and a subset is a set that contains only elements that are also in another set. If set A is a subset of set B, then all elements of A are also elements of B.
The number of subsets of a set with n elements is 2^n. So, if set A has n elements and set B has m elements (where m > n), the number of subsets of A is 2^n and the number of subsets of B is 2^m. The number of ways that A and B can have subsets is the product of the number of subsets of A and the number of subsets of B, or (2^n) * (2^m) = 2^(n+m).
Learn more about Subset Ways Calculation here:
https://brainly.com/question/13391651
#SPJ4
The girls’ swim team is hosting a fund raiser. They would like to raise at least $500. They are selling candles for $5 and flower arrangements for $6. The girls estimate that they will sell less than 200 items. Let c represent candles and f represent flower arrangements. Which system of inequalities represents this situation?
Answers
The system of inequalities represents this situation is:
c + f ≤ 200
5c + 6f ≥ 500
What is inequality in math?A statement of an order relationship—greater than, greater than or equal to, less than, or less than or equal to—between two numbers or algebraic expressions.
Let c represent candles arrangements
Let f represent flower arrangements.
The girls estimate that at most they will sell 200 items.
The equation will be:
c + f ≤ 200
They would like to raise at least $500. They are selling candles for $5 and flower arrangements for $6.
$5 × c + $6 × f ≥ $500
5c + 6f ≥ 500
Therefore, the system of inequalities is given as:
c + f ≤ 200
5c + 6f ≥ 500
Learn more about System of inequality at:
https://brainly.com/question/19526736
#SPJ1
What is the vertex of f(x) = |x + 8| – 3?
(-8,-3)
(-8,3)
(8,-3)
(8,3)
Answers
Answer: A.(-8,-3)
The vertex of the function f(x) = |x + 8| - 3 is (-8, -3).
What is an Equation?An equation is the statement of two expressions located on two sides connected with an equal to sign. The two sides of an equation is usually called as left hand side and right hand side.
Given is an absolute value function,
f(x) = |x + 8| – 3
For a function of the form,
f(X) = a |x - h| + k, the vertex of the function is the point (h, k).
Comparing the equation with the given one,
f(x) = |x + 8| – 3
f(x) = |x - (-8)| + (-3)
So we get, h = -8 and k = -3.
So vertex is (-8, -3).
Hence the vertex is (-8, -3).
Learn more about Absolute Value functions here :
https://brainly.com/question/14364803
#SPJ7
HELP ME PLEASE ITS DUE TODAY AND EXPLAIN HOW U GOT IT AND ILL MARK U THE BRAINLIEST!!!!

Answers
Answer: p= 1/7
Step-by-step explanation:
5/7=p+4/7
-p=4/7-5/7
-p=-1/7
P=1/7
Area of Square P = 17 cm2.
Area of Square R = 50 cm2.
Work out the area of Square Q.

Answers
Answer:
33
Step-by-step explanation:
(\((\sqrt{50})^{2} =(\sqrt{17})^{2}+a^{2} \\33=a^{2}\)
Pythagoras for that q side
\(\sqrt{33} *\sqrt{33} =33\)
the area
need help with this question

Answers
The explicit formula for the nth term of the sequence 14,16,18,... is aₙ = 2n + 12.
What is an explicit formula?
The explicit equations for L-functions are the relationships that Riemann introduced for the Riemann zeta function between sums over an L-complex function's number zeroes and sums over prime powers.
Here, we have
Given: the sequence 14,16,18,….
First term a₁ = 14
Common difference d = 16 - 14 = 2
Now, plug the values into the above formula and simplify.
aₙ = a₁ + d( n - 1 )
aₙ = 14 + 2( n - 1 )
aₙ = 14 + 2n - 2
aₙ = 14 - 2 + 2n
aₙ = 2n + 12
Hence, the explicit formula is aₙ = 2n + 12.
To learn more about the explicit formula from the given link
https://brainly.com/question/9859279
#SPJ1
kiran wants to make a larger scale drawing of the same classroom which of these aclales could he use
htx
Answers
Kiran would choose scale of 1 to 50.
What is Scale Factor?To adjust the size of a figure without altering its shape, a scale factor is a number or conversion factor that is utilised. It is employed to change the size of an object. If the original figure's dimensions and the dilated (increased or lowered) figure's dimensions are known, the scale factor can be determined.
Given:
As, The scale “1 inch to 6 feet” is equivalent to the scale “1 to 72,” because there are 72 inches in 6 feet.
The scale “1 to 100” would make a scale drawing that is smaller than the scale “1 to 72,” because each inch on the new drawing would represent more actual length.
The scale “1 to 50” would make a scale drawing that is larger than the scale “1 to 72,” because Kiran would need more inches on the drawing to represent the same actual length.
Learn more about scale factor here:
https://brainly.com/question/29464385
#SPJ1
The options are as follow:
1 to 50
1 to 72
1 to 100
If seven is subtracted from six times a number, the result is ten
Answers
Answer:
17/6
Step-by-step explanation:
6x-7=10
6x=10+7
6x=17
x=17/6
If 19 ounces is $5.32 then how much is 1 ounce worth?
Answers
Answer:
$3.57
Step-by-step explanation:
19/5.32=3.571...
rounded it equals 3.57
hope this helps :3
if it did pls mark brainliest
If the number of bacteria in a colony doubles every 9 hours and there is currently apopulation of 10,000 bacteria, what will the population be 18 hours from now?
Answers
After 9 hours, the population of the bacteria will be twice the initial population, it means:
\(2\cdot10000=20000\)After other 9 hours, the population will be two times 20000, it means:
\(2\cdot10000=40000\)According to this, after 18 hours the population of the bacteria will be 40000.
a computer that costs $4600 new has a book value of $3000 after 2 years. find the value of the computer after 3 years by using the exponential model y
Answers
The value of the computer with initial value $4600 after 3 years using the exponential model is equal to $2422.39 (approximately).
Cost of new computer = $4600
Book value after 2 years = $3000
use the exponential model,
y = a × \(e^{(-kt)}\)
where y is the value of the computer after t years,
a is the initial value of the computer when t=0,
k is a constant,
and e is the base of the natural logarithm.
Find the value of k using the information given,
y(2) = 3000
⇒3000 = a × \(e^{(-2k)}\)
y(0) = 4600
⇒ 4600 = a × e⁰
⇒ 4600 = a
Dividing the two equations, we get,
⇒3000/4600 = \(e^{(-2k)}\)
⇒0.6522 = \(e^{(-2k)}\)
Taking the natural logarithm of both sides, we get,
⇒ -2k = ln (0.6522 )
Solving for k, we get,
⇒ k = -0.4276 /2
⇒ k = - 0.2138
So the exponential model for the value of the computer is,
y = 4600 × \(e^{(-0.2138 \times t)}\)
To find the value of the computer after 3 years, we can plug in t=3,
y(3) = 4600 × \(e^{(-0.2138 \times 3)}\)
= 4600 × \(e^{(-0.6413)}\)
= 4600 × 0.5266
= 2422.39
Therefore, the value of the computer after 3 years using the exponential model is approximately $2422.39.
Learn more about exponential model here
brainly.com/question/28596571
#SPJ4
i need help plzzzzz!!!!

Answers
Answer:
help with what?
Step-by-step explanation:
Explanation:
Simplify the expression ✔️72What is the coefficient aWhat is the radicand b
Answers
we have the expression
\(\sqrt[]{72}\)Remember that
\(72=2^3\cdot3^2\)substitute
\(\sqrt[]{2^3\cdot3^2}=2\cdot3\sqrt[]{2}=6\sqrt[]{2}\)therefore
a=6
b=2
random variables and have joint pdf 1/50 0
Answers
Based on your question, it sounds like you are asking about random variables that have a joint probability density function (PDF) of 1/50 over a certain range of values.
In probability theory, a random variable is a variable whose value is determined by chance. It can take on a range of possible values, and the probabilities of each possible value occurring can be described using a probability distribution.
A joint probability density function is a function that describes the probabilities of two or more random variables taking on specific values simultaneously. In your case, you have two random variables that have a joint PDF of 1/50.
Without knowing the specific range of values over which the PDF is defined, it's hard to provide a more detailed answer. However, here are a few general observations about random variables and joint PDFs:
- Random variables can be either discrete or continuous. Discrete random variables take on specific, countable values (e.g. the number of heads in a series of coin tosses), while continuous random variables can take on any value within a certain range (e.g. the height of a randomly selected person).
- A joint PDF is typically used to describe the behavior of two or more continuous random variables. It gives the probability density at each point in the two-dimensional space defined by the values of the two variables.
- The total probability over the entire range of values for a joint PDF must sum to 1. This ensures that the probability of all possible outcomes occurring is equal to 1.
I hope this helps! If you have any further questions or clarifications, please let me know.
It seems that you are asking about random variables with a joint probability density function (pdf) of 1/50. Random variables are quantities that can take on different values according to some probability distribution. When two or more random variables are considered together, their relationship can be described using a joint pdf. In this case, the joint pdf is 1/50, indicating that the probability of a specific combination of these random variables is 1/50.
To learn more about probability visit;
https://brainly.com/question/30034780
#SPJ11