simplify 247+13 all the work please
Answers
Answer:
247+13=260
Step-by-step explanation:

Related Questions
Suppose that a biased coin that lands on heads with probability p is flipped 10 times. Given that we get exactly 6 heads out of 10 coin flips, find the conditional probability that the first 3 outcomes are (a) H,T,T (meaning that the first flips results in heads, the second in tails, and the third in tails).(b) T, H, T
Answers
The conditional probability
a) 5/36 - H, T, T
B) 5/36 - T, H, T
We have, we get exactly 6 heads out of 10 coin flips.
The probability of getting the head is p and the probability of getting the tail is 1-p.
In the first 3 tosses, the probability of getting H, T, T (in that order) is:
p(HTT) = p(1-p)(1-p) = p(1-p)²
Similarly, the probability of getting THT (in that order) is:
p(THT) = (1-p)p(1-p) = p(1-p)²
Note that since the coin is biased, the probability of getting heads or tails is not necessarily 1/2.
Let event A = "first 3 outcomes are H, T, T" and event B = "exactly 6 heads in 10 tosses".
(a) P(A|B), the conditional probability of A given B.
P(A) = p(1-p)² as shown above
P(B) = The number of ways to get exactly 6 heads in 10 tosses multiplied by the probability of getting any one of these ways.
P(B) = (10 choose 6) p⁶(1-p)⁴
Let C be the event "exactly 3 of the last 7 tosses are heads".
The probability of C is given by: P(C) = (7 choose 3) p³(1-p)⁴
Therefore, P(B) = P(C) x p³
P(A and B) is the probability of getting exactly 6 heads in the first 10 tosses and the first 3 tosses are H, T, T. This is the same as the probability of getting exactly 3 heads in the last 7 tosses and the last toss is tails (because the total number of heads is 6 and the first three tosses are H, T, T).
P(A and B) = (7 choose 3) p³(1-p)⁴ (1-p)
P(A|B) = P(A and B)/P(B)
P(A|B) = [ (7 choose 3) p³(1-p)⁴ (1-p) ] / [ (10 choose 6) p⁶(1-p)⁴ ]
P(A|B) = (7 choose 3)/(10 choose 6)
P(A|B) = 35/252
P(A|B) = 5/36
(b) Similarly, P(B) = (10 choose 6) p⁶(1-p)⁴, P(A) = p(1-p)² as shown above, and P(C) = (7 choose 3) p⁴(1-p)³.
Also,
P(B) = P(C) x (1-p)³P(A and B) is the probability of getting exactly 6 heads in the first 10 tosses and the first 3 tosses are T, H, T. This is the same as the probability of getting exactly 3 heads in the last 7 tosses and the last two tosses are H, T (because the total number of heads is 6 and the first three tosses are T, H, T).
P(A and B) = (7 choose 3) p⁴(1-p)³ p(1-p)
P(A|B) = P(A and B)/P(B) = [ (7 choose 3) p⁴(1-p)³ p(1-p) ] / [ (10 choose 6) p⁶(1-p)⁴ ]
P(A|B) = (7 choose 3)/(10 choose 6)
P(A|B) = 35/252
P(A|B) = 5/36
Therefore, the conditional probability that the first 3 outcomes are (a) H,T,T is 5/36 and that the first 3 outcomes are (b) T,H,T is 5/36.
To know more about the "conditional probability": https://brainly.com/question/23382435
#SPJ11
Save Acme Annuities recently offered an annuity that pays 3.9% compounded monthly. What equal monthly deposit should be made into this annuity in order to have $100,000 in 12 years? The amount of each deposit should be $ (Round to the nearest cent.)
Answers
To have $100,000 in 12 years with a 3.9% compounded monthly annuity, the equal monthly deposit needed would be approximately $653.44.
To calculate the monthly deposit, we can use the formula for future value of an annuity:
FV = P * ((1 + r/n)^(n*t) - 1) / (r/n),
where FV is the desired future value ($100,000), P is the monthly deposit, r is the annual interest rate (3.9% or 0.039), n is the number of compounding periods per year (12 for monthly compounding), and t is the number of years (12).
Plugging in the values into the formula:
100,000 = P * ((1 + 0.039/12)^(12*12) - 1) / (0.039/12).
Solving this equation for P gives us the monthly deposit of approximately $653.44.
To learn more about future value of an annuity, click here: brainly.com/question/28195816
#SPJ11
Use the graph below to evaluate f(0) and f(2)

Answers
f(2) = 4
The first answer choice is correct.
Find the value of x for which m || n.

Answers
Answer:
40
Step-by-step explanation:
The angles are equal to eachother so 4x-26 = 3x+14
Welcome, Detective Percent. Recently, there have been many reported scams. After weeks of investigations, you finally tracked down the address of the mastermind. He is an expert in %. He knows you are here to catch him and is in the midst of destroying all the evidence. He needs 30 minutes for the whole process to complete. You have to get through all the locks (full of percentages) to get to his secret chamber before all the evidences are gone.

Answers
Answer:
filthy Frank always told ppl who had anime pic where weeaboos
d = 8 cm
|d:
= 8 cm
Find the
volume of the
cactus
Answers
Without specific information about the cactus's shape or dimensions, it is not possible to accurately determine its volume.
Calculating the volume of a cactus based solely on its size of 8 cm is challenging without additional information about its shape or dimensions. Cacti come in various forms, including tall columnar cacti, spherical or globular cacti and branching cacti, each with distinct volume calculations.
I can provide you with a general overview of cacti and their unique characteristics.
Cacti are succulent plants that belong to the family Cactaceae.
They are typically found in arid and desert regions, known for their ability to store water in their stems, leaves, or roots.
This adaptation allows them to survive in dry environments with limited rainfall.
The volume of a cactus is typically determined by its shape and dimensions.
For instance, a cylindrical cactus would have a volume calculated using the formula for the volume of a cylinder, which is given by:
Volume = π × (radius)² × height
Without specific information about the cactus's shape or dimensions, it is not possible to accurately determine its volume.
If you have more details about the cactus, such as its specific shape, measurements, or a photo, I would be happy to assist you further in calculating its volume.
For similar questions on cactus's
https://brainly.com/question/10270193
#SPJ8

help me please need help

Answers
Answer:
Step-by-step explanation:
1. x -> opposite side of 48°
o → hypotenuse
b → adjacent side of 48°
\(\sf Sin \ 48^\circ = \dfrac{opposite \ side }{hypotenuse}\\\\\\0.7431 = \dfrac{15}{o}\\\\\\0.74 * o = 15\\\\\\ o = \dfrac{15}{0.74}\\\\\\\)
o = 20.27
\(\sf cos \ 48^\circ = \dfrac{adjacent \ side }{hypotenuse}\\\\\\0.67 =\dfrac{b}{o}\\\\\\0.67=\dfrac{b}{20.27}\)
b = 0.67*20.27
b = 13.58
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
2) i → opposite side of 25°
n → adjacent side of 25°
\(\sf Sin \ 25 =\dfrac{i}{t}\\\\\\0.42=\dfrac{i}{30}\\\\\\0.42*30=i\)
i = 12.6
\(\sf Cos \ 30^\circ =\dfrac{n}{t}\\\\0.91=\dfrac{n}{30}\\\\\\0.91*30 = n\)
n = 27.3
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
3) a → opposite side of 70°
e → adjacent side of 70°
\(Sin \ 70^\circ =\dfrac{a}{l}\\\\0.94 =\dfrac{a}{25}\\\\0.94*25=a\)
a = 23.5
\(\sf Cos \ 70^\circ =\dfrac{e}{l}\\\\0.34=\dfrac{e}{25}\\\\0.34*25=e\)
e = 8.5
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
4)
\(\sf Sin \ 52^\circ = \dfrac{x}{75}\\\\0.79*75=x\\\)
x = 59.25
\(\sf Cos \ 52^\circ = \dfrac{z}{75}\\\\0.62*75 =z\)
z = 46.5
The questions are in the picture. please answer showing work
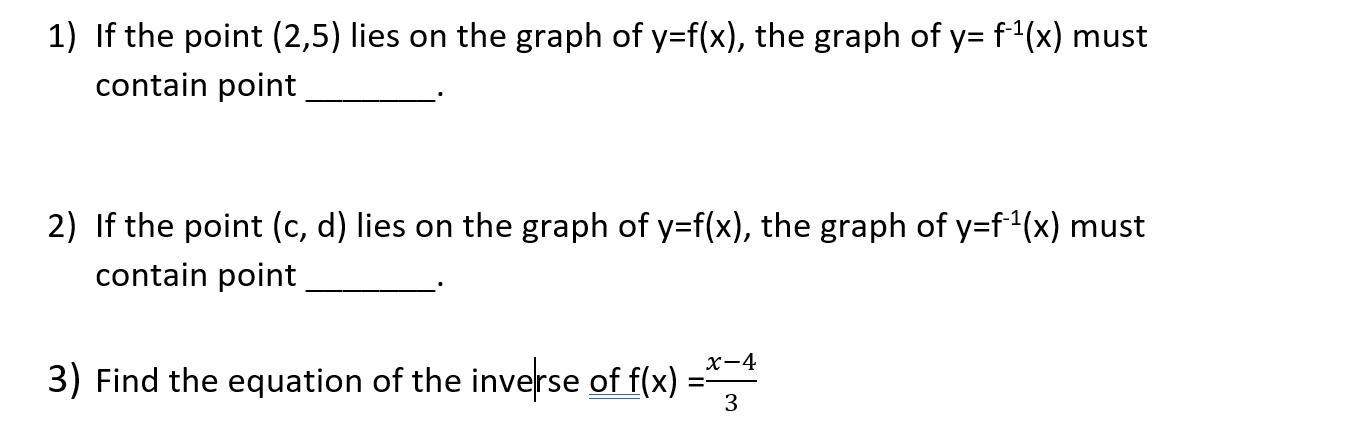
Answers
Answer:
what class is this?
Step-by-step explanation:
: Let ∆PQR triangle with vertices P= (2,4),Q = (2,2),R =(6,2). Reflect the triangle in line y=-1
Rotate the triangle 90° in anti clockwise about the point R of the triangle
Answers
The resulting triangle after reflecting ∆PQR in the line y = -1 and rotating it 90° counterclockwise about the point R is ∆P''Q''R'' with vertices P''(5, 2), Q''(5, 2), and R''(6, -2).
To reflect the triangle ∆PQR in the line y = -1, we can find the images of each vertex by reflecting them across the line.
The reflection of a point (x, y) across the line y = -1 can be obtained by keeping the x-coordinate the same and negating the y-coordinate.
For vertex P(2, 4):
The image of P after reflection will be P' with coordinates (2, -3).
For vertex Q(2, 2):
The image of Q after reflection will be Q' with coordinates (2, -3).
For vertex R(6, 2):
The image of R after reflection will be R' with coordinates (6, -2).
Now, to rotate the reflected triangle 90° counterclockwise about the point R(6, -2), we can use the rotation formulas.
The rotation of a point (x, y) counterclockwise by 90° about the point (a, b) can be obtained using the following formulas:
x' = a + (y - b)
y' = b - (x - a)
Applying these formulas to each vertex of the reflected triangle:
For vertex P', which is (2, -3):
x' = 6 + (-3 - (-2)) = 6 + (-1) = 5
y' = -2 - (2 - 6) = -2 - (-4) = 2
The image of P' after rotation will be P'' with coordinates (5, 2).
For vertex Q', which is (2, -3):
x' = 6 + (-3 - (-2)) = 6 + (-1) = 5
y' = -2 - (2 - 6) = -2 - (-4) = 2
The image of Q' after rotation will be Q'' with coordinates (5, 2).
For vertex R', which is (6, -2):
x' = 6 + (-2 - (-2)) = 6 + (0) = 6
y' = -2 - (6 - 6) = -2 - (0) = -2
The image of R' after rotation will be R'' with coordinates (6, -2).
Therefore, the resulting triangle after reflecting ∆PQR in the line y = -1 and rotating it 90° counterclockwise about the point R is ∆P''Q''R'' with vertices P''(5, 2), Q''(5, 2), and R''(6, -2).
Learn more about triangle here:
https://brainly.com/question/2773823
#SPJ11
David has kept track of his family’s grocery bills for the past
10 weeks, as shown in the table.
Week 1 2 3 4 5 6 7. 8 9 10
Bill ($) 92 106 129 115 100 84 110 156
98 87
Would you choose to use a histogram, a circle graph, or a line graph to
display the data? Explain your choice.
Answers
Answer:
it is more easier to use a histogram and accurate
Answer:
Line graph
Step-by-step explanation:
A line graph is specifically used to display data that changes over time, a line plot uses several points connected by straight lines on an x and y axis.
I wouldn't choose a histogram because a histogram is used to summarize continuous data.
As well as I wouldn't use a circle graph becasue it is often used to show the percentage of of population who gave a certain answer.
I need help ASAP! What is the expanded form of this number
15.306
A. (1 x 10) + (5 x 1) + (3 x 1/10) + (6 x 1/1000)
B. (1×10) + (5×1) + (3×110) + (6× 1/1000)
C. (1×10) + (5×1) + (3×1/100) +(6×1/100)
D. (1×10) + (5×1) + (3×1/100) + (6×1/1,000)
Answers
Answer:
the answer is A
So basically it's simple just use some scientific calculator and put the number one by one with the bracket because there's a rule of mathematics which we call BODMAS

Is the graph proportional?

Answers
Answer:
Yes, the graph represents a proportional relationship. No, the graph does not represent a proportional relationship. It is a straight line, but it does not intersect the point (0, 0).
1. Consider a consumer with utility function
u(x1, x2) = min ( 4 x1 + x2, x1 + 2 x2)
(a) Draw indifference curves passing through points (2; 2), (1; 2) and (4; 2) (Note:
these points may lie on different indifference curves). Make sure you correctly
determine kink points.
(b) Determine all properties of the preferences that you can deduce from the shape of
indifference curves or utility function. For each claimed property, provide either
a formal proof or a graphical visualization that will clearly indicate that the
claimed property holds.
(c) When X -> R2+, does UMP have a solution when Pk = 0? What property of the
preference relation did you use to get your answer?
(d) Assume that prices are positive. Derive the Walrasian demand of each good. Is the
Walrasian demand always single valued? [Hint: graphically depicting the UMP
can pin down the maximizing bundles. If p1=p2 > 4 what can you say about the
location of the utility-maximizing consumption bundle? What is the location if
4 < p1=p2 < 1=2? What about prices such that p1=p2 < 1=2?]
(e) Let p1 = p2 = 1 and w = $60. Suppose that the consumer receives a $10 voucher
from the government that he can spend only on good 1. Draw the new budget
set of the consumer and calculate the quantity of each good demanded by the
consumer. Does receiving the voucher make consumer better-off?
(f) Suppose instead that the government allows the consumer to choose between a
cash payment of $10 that can be spent on both goods and a $10 voucher that
can be spent on good 1 only. Which one would the consumer choose and why?
Would your answer change if the government's assistance were $30? Explain your
answer.
Answers
(a) By plugging in different values for x1, we can plot the indifference curves passing through the given points (2, 2), (1, 2), and (4, 2).
(b) The shape of the indifference curves shows convexity.
(c) The property used to determine this is the non-satiation property of preferences.
(d) The Walrasian demand may not always be single-valued.
(e) Receiving the voucher makes the consumer better-off .
(f) The cash payment allows the consumer to maximize utility by making trade-offs
For 4x1 + x2 = x1 + 2x2, rearranging the equation gives x2 = 3x1, representing the linear part of the indifference curves.
For x1 + 2x2 = 4x1 + x2, rearranging the equation gives x2 = 3x1, representing the kink in the indifference curves.
By substituting different values for x1, we can plot the indifference curves. They will be upward sloping straight lines with a kink at x2 = 3x1.
(b) Properties of the preferences deduced from the shape of indifference curves and utility function:
Diminishing Marginal Rate of Substitution (MRS): Indifference curves are convex, indicating diminishing MRS. The consumer is willing to give up less of one good as they consume more of it, holding the other good constant.
Non-Satiation: Indifference curves slope upwards, showing that the consumer prefers more of both goods. They always prefer bundles with higher quantities.
Convex Preferences: The kink in the indifference curves indicates convexity, implying risk aversion. The consumer is willing to trade goods at different rates depending on the initial allocation.
(c) UMP does not have a solution when Pk = 0 and X -> R2+. This violates the assumption of finite resources and prices required for utility maximization. The property used is non-satiation, as a consumer will always choose an infinite quantity of goods when they are available at zero price.
(d) Walrasian demand depends on relative prices:
If p1 = p2 > 4, the maximizing bundle lies on the linear portion of indifference curves, where x2 = 3x1.
If 4 < p1 = p2 < 1/2, the maximizing bundle lies on the linear portion of indifference curves but at lower x1 and x2.
If p1 = p2 < 1/2, the maximizing bundle lies at the kink point where x1 = x2.
Walrasian demand may not be single-valued due to the shape of indifference curves and the kink point, allowing for multiple optimal solutions based on relative prices.
(e) Given p1 = p2 = 1 and w = $60, the initial budget set is x1 + x2 = 60. With a $10 voucher for good 1, the new budget set becomes x1 + x2 = 70. Since p1 = 1, the consumer spends the voucher on good 1, resulting in x1 = 20 and x2 = 40. Receiving the voucher improves the consumer's welfare by allowing more consumption of good 1 without reducing good 2.
(f) If given the choice between a $10 cash payment and a $10 voucher for good 1 only, the consumer would choose the cash payment. It provides flexibility to allocate the funds based on individual preferences. The answer remains the same even if the assistance were $30, as the cash payment still allows optimal allocation based on preferences. Cash payment offers greater utility-maximizing options compared to the voucher, which restricts choices.
To know more about indifference curves, visit;
https://brainly.com/question/32705949
#SPJ11
The sum of 4 and a number
Answers
Answer:
The sum of 4 and X
Step-by-step explanation:
Determine the value of x for which rls if
.
m2i = 80 - X; and
mz2 = 90 - 2x
.

Answers
Answer:
x = 10
Step-by-step explanation:
For the lines to be parallel, the two angles must have the same measure:
80 - x = 90 - 2x
x = 10 . . . . . . . . . add 2x-80
The value of x must be 10 to make the lines parallel.
Find the perimeter.
Write your answer as a fraction or as a whole or mixed number.
3
mm
4
M
3
mm
|*
mm
3
mm
Last one for today thank youu

Answers
Answer:
3mm
Step-by-step explanation:
4 (3/4)
4x3/4
=3
brainiest please
Answer:
3 mm⠀
Step-by-step explanation:
⠀
We know,
\({\longrightarrow \qquad \boldsymbol{\pmb{Perimeter_{(square)} \it=4a }}}\)
⠀
Where,
a is the side length of the square. Here, a = \( \sf \: \dfrac{3}{4} \) mm⠀
Now, Substituting the values in the formula :
⠀
\({\longrightarrow \qquad {\rm{Perimeter_{(square)} = \it4 \times \it \dfrac{3}{4} }}}\)
⠀
\({\longrightarrow \qquad {\rm{Perimeter_{(square)} = \it \cancel4 \times \it \dfrac{3}{ \cancel4} }}}\)
⠀
\({\longrightarrow \qquad {\boldsymbol {\pmb{Perimeter_{(square)} = 3 }}}}\)
⠀
Therefore,
The perimeter of the square is 3 mmwhat is the answer? I'll give brainiest to whoever is right

Answers
Answer:
5) 0 6 ) 1/4
Step-by-step explanation:
So the slope ( gradient ) of line E is 0 because it is straight and it as no slope
The slope of line F is 1/4 because:
Gradient = y^2 - y^1 / x^2 - x^1
Gradient = 2-0 / 6- -2
Gradient= 2 / 8
2/8 in lowest term is 1/4
YOU MIGHT AVE A DIFFERENT METHOD BUT ANSWERS MUST BE THE SAME.
HOPE IT HELPED
Please help!!!!!! Hurry i only have 10 mins ill give brainy
Which operation should be used to solve LaTeX: \frac{x}{3} = 15x3=15 ?
Group of answer choices
+ 3
÷ 3
x 3
– 3
Answers
What is the result 3 x 6 ?
Answers
Answer:
Step-by-step explanation:
3*6=18
Find The Area Of The Region. Interior Of R = 9 + 7 Sin Θ (Below The Polar Axis) 2) Find The Area Of The Region. Two Petals Of R = 8 Sin(3θ) 3) Find Dy/Dx.
1) Find the area of the region.
Interior of r = 9 + 7 sin θ (below the polar axis)
2) Find the area of the region.
Two petals of r = 8 sin(3θ)
3) Find dy/dx.
x=\sqrt[3]{t}
y=3-t
Answers
To find the area of the region interior to r = 9 + 7sin(θ) below the polar axis, we can integrate the function from the lower bound of θ to the upper bound of θ and take the absolute value of the integral.
To find the area of the region formed by two petals of r = 8sin(3θ), we can integrate the function over the appropriate range of θ and take the absolute value of the integral. To find dy/dx for the given parametric equations x = t^(1/3) and y = 3 - t, we differentiate y with respect to t and x with respect to t and then divide dy/dt by dx/dt.
To find the area of the region interior to r = 9 + 7sin(θ) below the polar axis, we need to evaluate the integral ∫[lower bound to upper bound] |1/2 * r^2 * dθ|. In this case, the lower bound and upper bound of θ will depend on the range of values where the function is below the polar axis. By integrating the expression, we can find the area of the region. To find the area of the region formed by two petals of r = 8sin(3θ), we need to evaluate the integral ∫[lower bound to upper bound] |1/2 * r^2 * dθ|.
The lower bound and upper bound of θ will depend on the range of values where the function forms the desired shape. By integrating the expression, we can calculate the area of the region. To find dy/dx for the parametric equations x = t^(1/3) and y = 3 - t, we differentiate both equations with respect to t. Taking the derivative of y with respect to t gives dy/dt = -1, and differentiating x with respect to t gives dx/dt = (1/3) * t^(-2/3). Finally, we can find dy/dx by dividing dy/dt by dx/dt, resulting in dy/dx = -3 * t^(2/3).
Learn more about polar axis here: brainly.com/question/16425265
#SPJ11
what is the written form for 12/(4-2.3)
Answers
Answer:
Twelve over the quantity of four minus two point three
Step-by-step explanation:
100 PTS!!!! The perimeter of a rectangle is 4(4x - 5) inches. the length of the sides of the rectangle are 2 x + 3 inches and 3x + 2 inches. WRITE AND SOLVE an EQUATION to find the length of each side of the rectangle. ( you have to show all work for branliest!!!!! :D)
Answers
Answer:
2 sides are \(\frac{33}{13}\) or 2.5
2 sides are \(\frac{47}{13}\) or 3.6
Step-by-step explanation:
There must be 2 2x+3s and 2 3x+2s
The perimeter is the sum of the sides (it has 4 sides)
2(2x+3) + 2(3x+2) = 4(4x-5)
distributive property
2*2x + 2*3
4x+6
other one
2*3x + 2*2
6x+4
perimeter
4*4x + 4*-5
16x-20
together...
(4x+6) + (6x+4) = 16x-20
add like terms
10x+10 = 16x-20
add 20 to both sides
10x+30 = 16x
subtract 10x from both sides
30 = 26x
divide by 26 on both sides
\(\frac{30}{26} = x\)
simplify
\(\frac{15}{13}\)
Substitute the x value
2 of the sides are 2x+3
so
\(2(\frac{15}{13} ) + 3\)
\(\frac{30}{13} + \frac{3}{1}\)
\(\frac{33}{13}\)
or 2.5
other sides
\(3(\frac{15}{13} ) + 2\)
\(\frac{45}{13} + \frac{2}{1}\)
\(\frac{47}{13}\) or 3.6
That's all I can say for now! Hope this helps and a thank won't hurt! :)
Question 3
The distance from Mason's house to Kevin's house is about 5 x 10 to the power of 5 inches. The distance from Mason's house to Chloe's house is about 8 x 10 to the power of 7 inches
The distance from Mason's house to Chloe's house is how many times greater than the distance from Mason's to Kevin's house?
Answers
9514 1404 393
Answer:
160
Step-by-step explanation:
Your calculator can compute the ratio of distances for you.
\(\dfrac{8\times10^7}{5\times10^5}=\dfrac{8}{5}\times10^{7-5}=1.6\times10^2=\boxed{160}\)
Chloe's house is 160 times as far as Mason's house.
-2+2-3+32+958-545+555458
Answers
Answer:
The answer is 555900
Step-by-step explanation:
-2 + 2 - 3 + 32 + 958 - 545 + 555458 = 555900
Thus, The answer is 555900
-TheUnknownScientist 72
Answer:
555900
Step-by-step explanation:
-2+2=0=0-3+32+958-545+5554580-3=-3=-3+32+958-545+555458-3+32=29=29+958-545+55545829+958=987=987-545+555458=987-545+555458=442+555458442+555458=555900=555900lia has taken a mathematics exam, and she wants to calculate an 88% confidence interval to represent the exam scores within her group of friends. what are the z statistics that fall at each line marking the middle 88% of scores in the distribution?
Answers
In the given scenario, in order to calculate an 88% confidence interval, the z statistics that fall at each line marking the middle 88% of scores in the distribution would be +/- 1.555 (from the table).
In a case of seeking 88% confidence interval, the implication is that there is 12% chance that the interval does not contain the true value i.e., α=0.12 Assuming a two-sided test, it means that there should be 6% chance attributed to each tail of the z statistics (distribution). Thus, zα/2= z0.06.This z value at α/2=0.06 is the coordinate of the Z-curve that has 6% of the distribution's area to its right, and thus 94% of the area to its left. It is determined by z-value by reverse-lookup in a z-table. Find the closest value in the table to 0.9400 as possible, then see what its row and column is. From observation, it is seen that 0.9394 and 0.9406 are in the table with z -values of 1.55 and 1.56 respectively.We use liner interpolation to find the experimental z-score:0.9400 is (0.9400-0.9406)/(0.9394-0.9406) = ½ way from 0.9406 to 0.0394So, the z-score for 0.9400 is approximately ½ way from 1.56 to 1.55, hence
Z score = 1.56+((1.55-1.56)*1/2 = 1.5550
Hence the z score = 1.5550
Learn more about Confidence interval:
https://brainly.com/question/17097944
#SPJ4
What percent of 120 is 180%
Answers
What percent of 120 is 180
we know that
120 represent the 100%
so
Applying proportion
100/120=x/180
solve for x
x=(100/120)*180
x=150%
the answer is 150%6x+1=8x-9
pls help i forgot how to do dis yall
Answers
Answer:
6x+1=8x-9
6x=8x-9-1
6x=8x-8
x
-2x+1=-9
-2x=-10
X=5
Find the possible value of n in the inequality -3n <81
a.n <27
b is wrong
c.n=27
d. n>-27
Answers
The correct answer is option (a) n < 27. By dividing both sides of the inequality by -3, we get n > -27.
To solve the inequality -3n < 81, we divide both sides by -3. Remember that when dividing by a negative number, the direction of the inequality sign changes. Dividing both sides by -3 gives us n > -27. So, the correct answer is option (d) n > -27.
The reasoning behind this is that dividing by -3 reverses the inequality sign, which means that the less than ("<") sign becomes a greater than (">") sign.
Option (a) n < 27 is incorrect because dividing by -3 changes the direction of the inequality. Option (b) is stated to be wrong. Option (c) n = 27 is incorrect because the original inequality is strict ("<") and not an equality ("=").
Therefore, By dividing both sides of -3n < 81 by -3, we get n > -27. Therefore, the correct answer is option (a) n < 27.
To learn more about inequality click here brainly.com/question/30231017
#SPJ11
Hallie can use the equation p = 4l + 4w + 4h to determine the sum of the lengths of the edges of a rectangular prism. She begins to solve the equation for h but runs out of time. Her partial work is shown below: Which expression should follow the subtraction in Hallie’s equation?
1(l + w)
2(l – w)
3(l+w/4)
4(l-w/2)
Answers
Answer:
1.( l+w)
Step-by-step explanation:
The complete question is given below
Her partial work is shown below: p = 4l + 4w + 4h
= l + w + h
h =
Which expression should follow the subtraction in Hallie’s equation?
h=l+w
Answer is 1. (l +w)
if you know how to do this pls help thankyou!

Answers
Answer : 49
I hope you understand sorry for the ugly writing
