Simplify the expression: 3 * | -25 ÷ 5 |
Answers
Related Questions
During a storm, a tree breaks 7 feet above the ground and falls to form a right triangle. If the top of the tree rests 23 feet from the base of the tree, approximately how tall was the tree before the storm? Multiple choice question. cross out A) 31 feet cross out B) 29 feet cross out C) 24 feet cross out D) 22 feet Tools are not currently accessible
Answers
Answer:
We can solve this problem using the Pythagorean theorem, which states that in a right triangle, the sum of the squares of the lengths of the legs (the sides adjacent to the right angle) is equal to the square of the length of the hypotenuse (the side opposite the right angle).
Let's let "h" be the height of the tree before it broke, and "x" be the distance from the base of the tree to where it broke. Then, we can set up the following equation using the Pythagorean theorem:
h^2 = x^2 + (h-7)^2
We also know that the top of the tree rests 23 feet from the base of the tree, so we can set up another equation:
x + 23 = h
Now we have two equations with two unknowns, which we can solve simultaneously. Rearranging the second equation, we get:
x = h - 23
Substituting this into the first equation, we get:
h^2 = (h-23)^2 + (h-7)^2
Expanding the squares and simplifying, we get:
0 = -46h + 552
Solving for h, we get:
h = 12
Therefore, the height of the tree before it broke was approximately 12 feet. Since none of the answer choices match this result, we cannot cross out any of the choices.
How many more pebbles will hansel and gretel need to drop after the last one on this part of the path to mark the 1000th step they take?
Answers
As per the given data, Hansel and Gretel will need to drop 90 more pebbles after the last one on this part of the path to mark the 1000th step they take.
To determine how many steps Hansel and Gretel have taken when they get to the last pebble on this part of the path, we can use the information given: they marked every 10 steps with a pebble.
If the last pebble marks the 910th step, we can calculate the total number of steps taken by multiplying the number of pebbles by 10. In this case, the number of pebbles is 91.
Therefore, the total number of steps Hansel and Gretel have taken is:
91 × 10 = 910
So, when they reach the last pebble on this part of the path, they have taken 910 steps.
Now, let's move on to the second challenge: How many more pebbles will Hansel and Gretel need to drop after the last one on this part of the path to mark the 1000th step they take?
If the last pebble marks the 910th step and they want to mark the 1000th step, we need to determine how many more steps they need to take.
To find out, we subtract the current step (910) from the desired step (1000):
1000 - 910 = 90
Therefore, Hansel and Gretel will need to drop 90 more pebbles after the last one on this part of the path to mark the 1000th step they take.
For more details regarding challenges, visit:
https://brainly.com/question/32352419
#SPJ1
Your question seems incomplete, the probable complete question is:
Counting More Pebbles Along the Path page 2 of 2 LDATE a CMALLENGE Hansel and Gretel used a pebble to mark every 10 steps as they walked along the path. How many steps have they taken when they get to the last pebble on this part of the path? 910 Use numbers or words to explain how you know. 91×10=910 b CHALLENGE How many more pebbles will Hansel and Gretel need to drop after the last one on this part of the path to mark the 1000 th step they take? Use numbers or words to explain how you figured it out.
There are 25 households in purok 2 of barangay Sta. Catalina. The barangay captain ordered 40 sacks of rice
weighing 30 kg each. How many kilograms of rice will each household receive?
Answers
9514 1404 393
Answer:
48 kg
Step-by-step explanation:
(40 sacks)×(30 kg/sack)/(25 households) = (1200/25) kg/household
= 48 kg/household
Each household will receive 48 kg of rice.
Suppose 30% of the U.S. population has green eyes. If a random sample of size 1200 U.S. citizens is drawn, then the probability that less than 348 U.S. citizens have green eyes is _______.
Answers
Answer:
P(X is less than 348) = 0.2148
Step-by-step explanation:
Given that:
Sample proportion (p) = 0.3
Sample size = 1200
Let X be the random variable that obeys a binomial distribution. Then;
\(X \sim Bin(n = 1200,p =0.3)\)
The Binomial can be approximated to normal with:
\(\mu = np = 1200 \times 0.3 \\ \\ \mu= 360\)
\(\sigma = \sqrt{np(1-p) } \\ \\ \sigma = \sqrt{1200 \times (0.3)(1-0.3) } \\ \\ \sigma = 15.875\)
To find:
P(X< 348)
So far we are approximating a discrete Binomial distribution using the continuous normal distribution. 348 lies between 347.5 and 348.5
Normal distribution:
x = 347.5, \(\mu\) = 360, \(\sigma\) = 15.875
Using the z test statistics;
\(z = \dfrac{x - \mu}{\sigma}\)
\(z = \dfrac{347.5 - 360}{15.875}\)
\(z = \dfrac{-12.50}{15.875}\)
z = -0.7874
z ≅ - 0.79
The p-value for P(X<347.5) = P(Z < -0.79)
From the z tables;
P(X<347.5) = 0.2148
Thus;
P(X is less than 348) = 0.2148
Solve for x
x^2 - 8x = -3
Answers
The solutions for the quadratic equation:
x^2 - 8x = -3
Are:
x = 7.6x = 0.4How to solve the quadratic equation?Here we want to solve the quadratic equation:
x^2 - 8x = -3
First we can move all the terms to the left side so we get:
x^2 - 8x + 3 = 0
Using the quadratic formula (or Bhaskara's formula) we can get the solutions for x as:
\(x = \frac{8 \pm \sqrt{(-8)^2 - 4*¨1*3} }{2*1} \\\\x = \frac{8 \pm 7.2 }{2}\)
Then the two solutions for the quadratic equation are:
x = (8 + 7.2)/2 = 7.6
x = (8 - 7.2)/2 =0.4
Learn more about quadratic equations by reading:
https://brainly.com/question/1214333
#SPJ1
264 divided by 8 what is the answer
Answers
Answer:
20.5 or 20 1/2
Step-by-step explanation:
calculator -.-
Answer:
2112
Step-by-step explanation:
:)
A box has the shape of a rectangular prism with height 28 cm. If the height is increased by 0.2cm, by how much does the surface area of the box increase? L=13 W=8.7 H=28
Answers
The surface area of the box increases by 27.4 cm² when the height is increased by 0.2 cm.
To find the increase in surface area, we first need to calculate the initial surface area of the box and then calculate the surface area after increasing the height.
The formula for the surface area of a rectangular prism is given by:
Surface Area = 2*(length width + length height + width*height)
Initial Surface Area:
Length (L) = 13 cm
Width (W) = 8.7 cm
Height (H) = 28 cm
Initial Surface Area = 2*(138.7 + 1328 + 8.7*28)
Next, we calculate the new surface area after increasing the height by 0.2 cm. The new height is:
New Height = Initial Height + Increase in Height = 28 cm + 0.2 cm
New Surface Area = 2*(138.7 + 13(28+0.2) + 8.7*(28+0.2))
To find the increase in surface area, we subtract the initial surface area from the new surface area:
Increase in Surface Area = New Surface Area - Initial Surface Area
Let's calculate the values:
Initial Surface Area = 2*(138.7 + 1328 + 8.728) = 2(113.1 + 364 + 243.6) = 2*(720.7) = 1441.4 cm²
New Surface Area = 2*(138.7 + 13(28+0.2) + 8.7*(28+0.2)) = 2*(113.1 + 377.2 + 244.1) = 2*(734.4) = 1468.8 cm²
Increase in Surface Area = New Surface Area - Initial Surface Area = 1468.8 cm² - 1441.4 cm² = 27.4 cm²
Therefore, the surface area of the box increases by 27.4 cm² when the height is increased by 0.2 cm.
For such more questions on Increase in surface area
https://brainly.com/question/23851972
#SPJ11
A study found that 85% of sports business executives surveyed believed that sponsor development of ________ in new venues will be a benefit of top-tier sponsorships in coming years.
Answers
Can you please help me
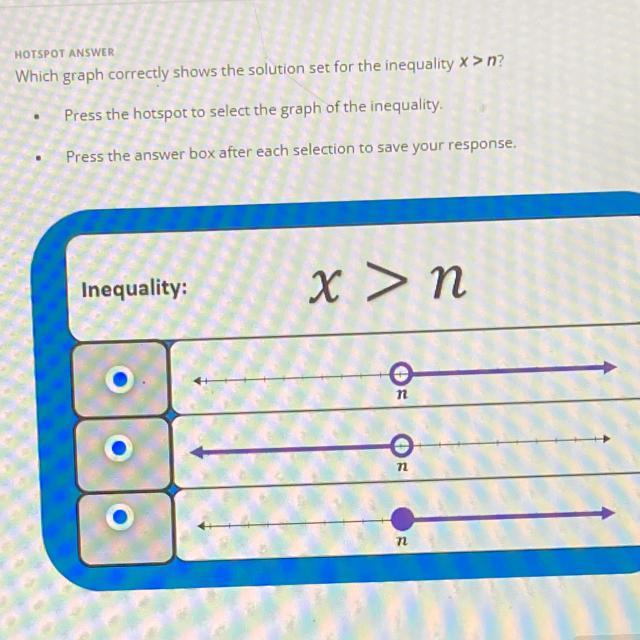
Answers
Answer:
first graph
Step-by-step explanation:
x > n
the graph will have an open circle at the value n , indicating that x cannot equal n ( note solid circle if x ≥ n )
the arrow from n will point in the right direction, indicating values of x greater than n.
the graph representing x > n is the first graph
For the following vectors, (a) find the dot product v•w ; (b) find the angle between v and w , (c) state whether the vectors are parallel, octagonal, or neither. V=-3i-4j, w=6i+8j
A- v•w
B-the angle between v and w is theta ^•?
C- the vectors v and w are?
Answers
B) The angle between vectors v and w can be found using the formula: cos(theta) = (v • w) / (||v|| ||w||), where ||v|| and ||w|| are the magnitudes of vectors v and w respectively.
First, we need to find ||v|| and ||w||:
||v|| = sqrt((-3)^2 + (-4)^2) = 5
||w|| = sqrt((6)^2 + (8)^2) = 10
Now, we can substitute in the values to get:
cos(theta) = (-50) / (5 * 10) = -1
theta = arccos(-1) = pi radians or 180 degrees.
Therefore, the angle between vectors v and w is 180 degrees.
C) Two vectors are parallel if their directions are the same, which can be determined by comparing their unit vectors.
The unit vector of v is:
v_hat = v / ||v|| = (-3/5)i + (-4/5)j
The unit vector of w is:
w_hat = w / ||w|| = (6/10)i + (8/10)j = (3/5)i + (4/5)j
We can see that the unit vectors are in opposite directions, which means that the vectors are anti-parallel or opposite. Therefore, the vectors v and w are neither parallel nor orthogonal.
simplify the following y^-1z^5×y^3z^2
Answers
Answer:=y^3z^7y
Step-by-step explanation:
a mathematics professor assigns two problems for homework and knows that the probability of a student solving the first problem is 0.90, the probability of solving the second is 0.45, and the probability of solving both is 0.20. (round your answers to three decimal places.)
Answers
The required probabilities for the given sections of the question are a) P(A|B) = 0.111, b) P(B|A) = 0.059.
Explain conditional probability?The probability of occurrence of any occasion A when one more occasion B corresponding to A has proactively happened is known as contingent likelihood.
According to question:A = occasion of tackling the first problem
B = occasion of tackling the second problem
Given
P(A) = 0.85
P(B) = 0.45
P(A and B) = 0.05
Section (a)
Jed has tackled the subsequent issue. So we're given that occasion B has occurred. We need to track down P(A|B) which is the likelihood of occasion An occurrence given B has occurred.
Utilize the restrictive likelihood equation
P(A|B) = P(A and B)/P(B)
P(A|B) = 0.05/0.45
P(A|B) = 0.111111
P(A|B) = 0.111
Part (b)
Same thought as to some degree (a), yet presently we need to track down P(B|A). We know occasion A has occurred and we need to find the likelihood of occasion B happening in light of A.
P(B|A) = P(B and A)/P(A)
P(B|A) = P(A and B)/P(A)
P(B|A) = 0.05/0.85
P(B|A) = 0.05882
P(B|A) = 0.059
Thus, required probability are a) P(A|B) = 0.111, b) P(B|A) = 0.059.
To know more about conditional probability visit:
brainly.com/question/11899923
#SPJ4
Correct question:
a mathematics professor assigns two problems for homework and knows that the probability of a student solving the first problem is 0.90, the probability of solving the second is 0.45, and the probability of solving both is 0.20. (round your answers to three decimal places.)
(a) Jed has solved the second problem. What is the probability he also solves the first problem? (b) Edna has solved the first problem. What is the probability she also solves the second problem?
Anu was checking her emails she casually told her friend siting next to her the ratio of unread emails in my inbox is 4:1 The total number of emails is 120 what is the number of unread emails in her inbox
Answers
In a case whereby Anu was checking her emails and she casually told her friend siting next to her the ratio of unread emails in my inbox is ratio 4:1 where the total number of emails is 120 then the number of unread emails in her inbox is 96mails.
How can the unread mails be calculated?The concept that will be used here is ratio. An ordered pair of numbers a and b, represented as a / b, is a ratio if b is not equal to 0. A proportion is an equation that sets two ratios at the same value. For instance, you could express the ratio as follows: 1: 3 if there is 1 boy and 3 girls (for every one boy there are 3 girls)
The total mails in her box is 120
The we can represent the unread mails as 4x and read mails be 1x
This can be expressed as :
(4x+1x)=120mails
5x=120mails
x=120/5
x=24
This implies that the uread mails(4×24)
=96mails
Then the number of the read mail =(1×24)=24mails
Learn more about emails at:
https://brainly.com/question/20731943
#SPJ1
Give an example of two different sets of data, in which both box plots have the same range and IQR and yet represent completely different data. Explain.
Answers
Answer:
set 1 and 2
Step-by-step explanation:
Set 1 has 10
Set 2 has 13
calculate the average power radiated by each square meter of the sun's surface. (hint: the formula for the surface area of a sphere is a
Answers
The average power radiated by each square meter of the sun's surface is approximately 386 W/m². This value is calculated by dividing the total power radiated by the sun (approx. 386 billion Megawatts) by its surface area (approx. 6.08 x 10¹⁸ square meters). The formula for the surface area of a sphere is 4πr².
Sun Power Output CalculationThe average power radiated by each square meter of the sun's surface can be calculated as follows:
Calculate the total power radiated by the sun:The total power radiated by the sun is approximately 386 billion
Megawatts (3.86 x 10³³ erg/s).
Calculate the surface area of the sun:The surface area of the sun can be calculated using the formula for
the surface area of a sphere:
A = 4πr², where r is the radius of the sun (approx. 6.96 x 10⁸
meters).
Plugging in the values, we get:
A = 4π (6.96 x 10⁸)² = 6.08 x 10¹⁸ square meters.
Divide the total power by the surface area:Finally, divide the total power by the surface area to get the
average power radiated by each square meter of the sun's surface:
P = 3.86 x 10³³ erg/s / 6.08 x 10¹⁸ m² = 386 W/m².
Learn more about Sun Power Output Calculation here:
https://brainly.com/question/30174924
#SPJ4
Sam takes 4 hours to peel 32 potatoes, while Josh takes 5 hours to peel 30 potatoes. (a) How long is it going to take both Sam and Josh to peel 100 potatoes together? (b) How many potatoes will they peel together in 12 hours?
Answers
We can define a rate as the quotient between two variables.
With this we will find:
a) 7.14 hours
b) 168 potatoes.
Knowing that Sam takes 4 hours to peel 32 potatoes, the rate at which he peels potatoes is:
S = (32 potatoes)/(4 hours) = 8 potatoes per hour.
And we know that Josh needs 5 hours to peel 30 potatoes, then Josh's rate is:
J = (30 potatoes)/(5 hours) = 6 potatoes per hour.
a) If Josh and Sam work together, then the rate at wich they work is:
(S + J)
And we want to find the time T such that they peel 100 potatoes.
Then we need to solve for T:
(S + J)*T = 100 potatoes
(8 potatoes per hour + 6 potatoes per hour)*T = 100 potatoes
(14 potatoes per hour)*T = 100
T = 100/(14 potatoes per hour) = 7.14 hours
So they need 7.14 hours to peel 100 potatoes.
b) Here we just need to compute:
(S + J)*12 hours
(14 potatoes per hour)*12 hours = 168 potatoes.
If you want to learn more, you can read:
https://brainly.com/question/24542879
both clocks ring toget (b) Two bells hanged at a school were adjusted at 10:00 am in such a way th one of them rings at the interval of every 45 minutes and another at every minutes. At what time will both bells ring together ?
Answers
The Least common multiple (LCM) The time at which both bells will ring together is 10:45 am, and the Subsequent times will be 11:30 am, 12:15 pm, 1:00 pm, and so on, with an interval of 45 minutes between each occurrence.
The time at which both bells will ring together, we need to find the least common multiple (LCM) of the intervals at which each bell rings.
The first bell rings every 45 minutes, and the second bell rings every minute. We want to find the point at which both intervals align, meaning they both divide evenly into the same amount of time.
To find the LCM, we can list the multiples of each interval until we find a common multiple.
Multiples of 45 minutes: 45, 90, 135, 180, 225, 270, 315, 360, 405, ...
Multiples of 1 minute: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, ...
From the lists above, we can observe that the least common multiple occurs when both intervals coincide at the same time, which is 45 minutes.
Thus, the two bells will ring together every 45 minutes.
If we consider the initial adjustment time of 10:00 am, the first time both bells will ring together is at 10:45 am. After that, they will continue to ring together every 45 minutes throughout the day.
Therefore, the time at which both bells will ring together is 10:45 am, and the subsequent times will be 11:30 am, 12:15 pm, 1:00 pm, and so on, with an interval of 45 minutes between each occurrence.
To know more about Least common multiple (LCM) .
https://brainly.com/question/16054958
#SPJ11
Convert 2,430 yards to km
Answers
Answer:
2.221992
Step-by-step explanation:
can i have the crown pls ૮ ♡ﻌ♡ა
Answer:
2.221
Step-by-step explanation:
SOMEONE PLEASE HELPP MEE

Answers
The end-points of the line segment will be negative 1.25 and 0.25.
What is a number line?A number line refers to a straight line in mathematics that has numbers arranged at regular intervals or portions along its width. A number line is often shown horizontally and can be postponed in any direction.
The length of the line segment is 1.50 units and the midpoint of the line segment is negative 0.50. Then the end-points of the line segment are given as,
⇒ - 0.50 ± (1.50) / 2
Simplify the expression, then we have
⇒ - 0.50 ± (1.50) / 2
⇒ - 0.50 - (1.50) / 2, - 0.50 + (1.50) / 2
⇒ - 0.50 - 0.75, - 0.50 + 0.75
⇒ - 1.25, 0.25
The end-points of the line fragment will be negative 1.25 and 0.25.
More about the number line link is given below.
https://brainly.com/question/13189025
#SPJ1

Determine the turning points and distinguish between them when necessary y=x³ - 3x - 9x + 4
Answers
The turning points of the function y = x³ - 3x² - 9x + 4 are (3, -23) and (-1, 9).
To determine the turning points of the given function y = x³ - 3x² - 9x + 4, we need to find the critical points where the derivative of the function is equal to zero.
1. Find the derivative of the function:
y' = 3x² - 6x - 9
2. Set the derivative equal to zero and solve for x:
3x² - 6x - 9 = 0
3. Factorize the quadratic equation:
3(x² - 2x - 3) = 0
4. Solve the quadratic equation by factoring or using the quadratic formula:
(x - 3)(x + 1) = 0
This gives us two possible values for x: x = 3 and x = -1.
5. Substitute these critical points back into the original function to find the corresponding y-values:
For x = 3:
y = (3)³ - 3(3)² - 9(3) + 4
= 27 - 27 - 27 + 4
= -23
For x = -1:
y = (-1)³ - 3(-1)² - 9(-1) + 4
= -1 - 3 + 9 + 4
= 9
6. Therefore, the turning points are (3, -23) and (-1, 9).
Note: It appears that there was a typo in the original equation, where the term "-9x" should have been "-3x²". The above solution assumes the corrected equation.
For more such questions on points, click on:
https://brainly.com/question/26865
#SPJ8
Adrienne has chickens and ducks on her farm. She has 48 chickens and 28 ducks. What ratio describes the number of ducks to the number of chickens?
Answers
The table shows the number of students graduating from an online university in selected year . Use a calculator to write a cubic model for the number of graduates in a given year since 2002. Then use the model to estimate the number of graduates in 2008.
Answers
There were approximately 5,184 graduates in 2008.
The cubic model is a useful tool for estimating the number of graduates in a given year, as it takes into account the trend of the data points. This allows us to make an educated guess about the number of graduates in a given year, despite not having data points for that year.The cubic model for the number of graduates from an online university since 2002 can be expressed as y = -7.8x^3 + 74.4x^2 + 437x - 9,150. Here, x is the number of years since 2002, and y is the number of graduates in that year. To estimate the number of graduates in 2008, we can plug in x = 6 into the equation, giving us y = 5,184. That is, there were approximately 5,184 graduates in 2008.
Learn more about cubic model here:
https://brainly.com/question/23134736
#SPJ4
Hello can someone please answer this question i will mark you the Brainliest

Answers
Answer:
A) 310 cm²
Step-by-step explanation:
The surface area is the area of the two-dimensional surfaces of this three-dimensional figure.
Start by multiplying each 5x4 rectangle. There are four of them that are visible from the front.
4(5 · 4) 4(20) = 80 cm²Now, find the surface area of the large rectangle in the back and the left side of the figure.
2(10 · 4) = 80 cm²Find the surface area of the top of this figure.
10 · 5 = 50 cm²5 · 5 = 25 cm²Find the surface area of the bottom of this figure (it's the same as the area of the top).
50 + 25 = 75 cm²Add all of the surface areas together to find the total surface area of the figure.
80 + 80 + 75 + 75 = 310 cm²√2x² + 7x + 5√2 = 0
find the roots of the following quadratic equation by factorization method
PLS HELP ME FAST
Answers
Step-by-step explanation:
√2x² + 7x +√2=0
2x + 7x + √ 2 =0
√2=9x
x = o.15713484
A scientist wants a 64 milliliter acid solution with a concentration of 8%. She has concentrations of 2% and 10%. How much
of each solution must she use to get the desired concentration?
Answers
Answer:
16 milliliters of 2% solution
48 milliliters of 10% solution
Step-by-step explanation:
x = 2% solution
y = 10% solution
System of Equations:
x + y = 64
.02x + .10y = 64(.08)
use Substitution: y = 64 - x
.02x + .10(64 - x) = 5.12
.02x + 6.4 - .10x = 5.12
-.08x = -1.28
x = 16
y = 64 - 16 which equals 48
A programmer plans to develop a new software system. In planning for the operating system that he will​ use, he needs to estimate the percentage of computers that use a new operating system. How many computers must be surveyed in order to be 99​% confident that his estimate is in error by no more than two percentage points question mark s?​a) Assume that nothing is known about the percentage of computers with new operating systems. n=_______.(Round up to the nearest​ integer.)b) Assume that a recent survey suggests that about 96​% of computers use a new operating system. n=_______.(Round up to the nearest​ integer.)
Answers
Answer:
a) \(n=\frac{0.5(1-0.5)}{(\frac{0.02}{2.58})^2}=4160.25\)
And rounded up we have that n=4161
b) \(n=\frac{0.96(1-0.96)}{(\frac{0.02}{2.58})^2}=639.01\)
And rounded up we have that n=640
Step-by-step explanation:
Part a
The confidence level is 99% , our significance level would be given by \(\alpha=1-0.99=0.01\) and \(\alpha/2 =0.005\). And the critical value would be given by:
\(z_{\alpha/2}=-2.58, z_{1-\alpha/2}=2.58\)
The margin of error for the proportion interval is given by this formula:
\( ME=z_{\alpha/2}\sqrt{\frac{\hat p (1-\hat p)}{n}}\) (a)
And on this case we have that \(ME =\pm 0.02\) and we are interested in order to find the value of n, if we solve n from equation (a) we got:
\(n=\frac{\hat p (1-\hat p)}{(\frac{ME}{z})^2}\) (b)
Since we don't have prior info for the true proportion we can use \(\hat p=0.5\). And replacing into equation (b) the values from part a we got:
\(n=\frac{0.5(1-0.5)}{(\frac{0.02}{2.58})^2}=4160.25\)
And rounded up we have that n=4161
Part b
For this case we have a prior estimation ofr the proportion:
\( \hat p=0.96\)
And replacing we got:
\(n=\frac{0.96(1-0.96)}{(\frac{0.02}{2.58})^2}=639.01\)
And rounded up we have that n=640
A baseball diamond is a square that is 90 feet on each side. What is the distance a catcher has to throw the ball from home to second base?
Answers
So 90 squared + 90 squared = c2
90 x 90= 8100 x 2 is equal to 16200.
16200= c2
The square root of 16200 is about 127.27 feet. That’s the answer
Line AB contains points A(4, 5) and B(9, 7). What is the slope of ?
– negative StartFraction 5 Over 2 EndFraction
– negative StartFraction 2 Over 5 EndFraction
StartFraction 2 Over 5 EndFraction
StartFraction 5 Over 2 EndFraction
Answers
The slope of line AB with points A(4, 5) and B(9, 7) is 2/5.
What is slope?The slope or gradient of a line is a number that describes both the direction and the steepness of the line.
We have,
A(4, 5) and B(9, 7)
The slope of a line with points A and B is given by:
= d - b / c - a
Where A(a, b) and B(c, d) are the coordinates of the points.
We have the points:
A(4, 5) = (a, b)
B(9, 7) = (c, d)
The slope of the line AB:
= (7 - 5) / (9 - 4) = 2 / 5
Therefore the slope of line AB with points A(4, 5) and B(9, 7) is 2/5.
Learn more about slopes here:
https://brainly.com/question/3605446
#SPJ1
In the diagram below, BD is parallel to XY What is the value of y?
.
B
**
O A. 20
O B. 130
O C. 110
D. 70
Answers
Answer:
\(y =110^\circ\)
Step-by-step explanation:
Given
See attachment for diagram
Required
Find y
From the attachment, 70 and y are interior angles.
So:
\(70 + y = 180\)
Solve for y
\(y = 180 - 70\)
\(y =110^\circ\)

I need help with graphing the points and solving it

Answers
We have a system of inequalities:
\(\begin{gathered} y\ge-2x-2 \\ y>\frac{1}{3}x \end{gathered}\)We can graph this inequalities as:
The points that satisfy both equations should be in the most shaded area (area marked with A)
If we graph the points listed, we get:
The point (-1,4) is the only one that satisfy both inequalities.
Answer: Point (-1,4) [Option B]

