Suppose y varies inversely with x, and y = 36 when x=112
What inverse variation equation relates x and y ?
Answers
The inverse variation equation that relates x and y is x = 4032 / y.
What is the equation that relates x and y?if two variables vary inversely, there is a negative relationship between both variables. the increase in one variable leads to a decrease in the other variable
The equation that represents inverse proportion : x = b/y
where b = constant of proportionality
112 = b /36
b = 36 x 112 = 4032
The equation : x = 4032 / y
To learn more about inverse proportion, please check: https://brainly.com/question/27233899
#SPJ1
Related Questions
What is the result of the division?

Answers
A shipping box is 36 inches by 24 inches by 18 inches
how many cubic feet can it hold
Answers
Answer:
To find the volume of the shipping box in cubic feet, we need to convert the dimensions from inches to feet and then calculate the volume.
Given:
Length = 36 inches
Width = 24 inches
Height = 18 inches
Converting the dimensions to feet:
Length = 36 inches / 12 inches/foot = 3 feet
Width = 24 inches / 12 inches/foot = 2 feet
Height = 18 inches / 12 inches/foot = 1.5 feet
Now, we can calculate the volume of the box by multiplying the length, width, and height:
Volume = Length * Width * Height
Volume = 3 feet * 2 feet * 1.5 feet
Volume = 9 cubic feet
Therefore, the shipping box can hold 9 cubic feet.
Step-by-step explanation:
First convert the units because it's asking for the cubic feet but they give us the measurements in inches.
To convert inches to feet we divide the number by 12.
36 ÷ 12 = 3
24 ÷ 12 = 2
18 ÷ 12 = 1.5
Now to find the volume, we multiply it all together.
3 × 2 × 1.5 = 9
It can hold 9 cubic feet.
Hope this helped!
The point (5, -2) is translated by (x,y)→
(x - 4, y + 5), then rotated 90°
clockwise. What are the coordinates of the final image?
Answers
Answer:
(1,3)
Step-by-step explanation:
hope it's help ful
The question is asked in the attached file,. Kindly someone answer it in the best way.

Answers
According to the Empirical Rule, 99.7% of the measures fall within 3 standard deviations of the mean in the normal distribution.
What does the Empirical Rule state?The Empirical Rule states that, for a normally distributed random variable, the symmetric distribution of scores is presented as follows:
The percentage of scores within one standard deviation of the mean of the distribution is of approximately 68%.The percentage of scores within two standard deviations of the mean of the distribution is of approximately 95%.The percentage of scores within three standard deviations of the mean off the distribution is of approximately 99.7%.More can be learned about the Empirical Rule at https://brainly.com/question/10093236
#SPJ1
how manys pounds of mixed nuts that contain 20% peanuts must eugene add to 16 pounds of mixed nuts that contain 70% peanuts to make a mixture with 60% peanuts?
help
Answers
We can add 10 pounds of mixed nuts that contain 20% peanuts by solving equations.
What are equations?Algebraically speaking, an equation is a statement that shows the equality of two mathematical expressions.
For instance, the two equations 3x + 5 and 14, which are separated by the 'equal' sign, make up the equation 3x + 5 = 14.
So, the quantity of mixed nuts we need is x pounds.
There are 0.70 pounds of peanuts in this mixture.
3 pounds of peanuts make up the 20% mix, or 0.20*15.
We got the equation:
0.70 x + 3 = 0.40(x + 15)
Now, solve this equation as follows:
0.70 x + 3 = 0.40(x + 15)
0.70 x + 3 = 0.40(x + 15)
0.70x + 3 = 0.40x + 6
0.70x - 0.40x = 6 - 3
0.30x = 3
x = 10 pounds
Therefore, we can add 10 pounds of mixed nuts that contain 20% peanuts by solving equations.
Know more about equations here:
brainly.com/question/28937794
#SPJ1
What is the volume of a rectangular prism if the length is 21 feet width is nine and height is seven that's not nice what is the volume of a rectangular prism if the length is 21 feet width is nine and height is 7 feet
Answers
The volume of the prism is 1323 feet³ (cubic feet).
Step-by-step explanation:1. Annotate the values.Length= 21 feet.
Width= 9 feet.
Height= 7 feet.
2. Find a formula.The formula to calculate the volume of rectangular prisms is the following:
\(\sf V_{RP} =l*w*h\); where "l" is the length; "w" is the width, and "h" is the height of the prism.
Check the attached image to see where these values are measured from.
3. Calculate.Substitute the variables in the formula by the values on step 1.
\(\sf V_{RP} =l*w*h=(21\ feet)*(9\ feet)*(7\ feet)=\boxed{\sf1323\ feet}.\)
The volume of the prism is 1323 feet³ (cubic feet).
-------------------------------------------------------------------------------------------------------
Learn more about calculations of volumes and operations around volume here:
https://brainly.com/question/30569232
https://brainly.com/question/29462977
https://brainly.com/question/28308963
https://brainly.com/question/31881728

Answer:
The volume of the rectangular prism is 1323 cubic feet.
Step-by-step explanation:
Step 1: Write down the formula for the volume of a rectangular prism:
\(\qquad\Large\boxed{\rm{\:\:\:V = l \times w \times h\:\:\:}}\)
Step 2: Substitute the given values for the length, width, and height:
\(\qquad\Large\rm{V = 21\: ft \times 9\: ft \times 7\: ft}\)
Step 3: Multiply the numbers together:
\(\qquad\Large\rm\implies{V = 1323\: ft^3}\)
Step 4: Write the final answer with the appropriate units:
The volume of the rectangular prism is 1323 cubic feet.
\(\blue{\overline{\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad}}\)
i will give mor points ans please
Answers
Answer:
Step-by-step explanation:
| − | = | + 9I
THERE ARE TWO POSSIBILITIES
2x-1=4x+9 and 2x-1=-4x-9
2x-4x=9+1 and 2x+4x=-9+1
-2x=10 and 6x=-8
x=-5 and x=-8/6
x=-5 and x=-4/3
SOLUTION SET ={-5,-4/3}
\(\frac{2x-1}{3}-\frac{3x}{4}=\frac{5}{6}\\ taking LCM\\\frac{8x-4-9x}{12}=\frac{5}{6}\\\frac{-1x-24}{12}=\frac{5}{6}\\ by cross multiplication\\6(-1x-4)=12*5\\-6x-24=60\\-6x=60+24\\-6x=84\\\\x=-14\\soltion set {-14}\)
\(10+\sqrt{10m-1}=13\\\sqrt{10m-1}=13-10\\\\\sqrt{10m-1}=3\\ taking square on both sides\\10m-1=3^2\\10m-1=9\\10m=9+1\\10m=10\\m=1\)
the number of solution to a linear equation is 1
2(x - 4) = 6 then x is ----7
Solution of | + | = − is ---------13/3,5/3
Урна содержит 10 белых и 10 черных шаров. Вынимают 5 раз по два шара (без возврата). С какой вероятностью каждый раз вынимали по 2 шара разного цвета?
An urn contains 10 white and 10 black balls. Two balls are taken out 5 times (without return). What is the probability that 2 balls of different colors were drawn each time?
Answers
Answer:
≈4,365%.
Step-by-step explanation:
1) для нахождения требуемой вероятности необходимо найти вероятность каждого из пяти выниманий, а затем перемножить их;
2) при каждом вынимании вероятности:
\(P_1=\frac{C^1_{10}*C^1_{10}}{C^2_{10}}=\frac{10}{19};\\P_2=\frac{C^1_9*C_9^1}{C^2_{18}}=\frac{9}{17};\\P_3=\frac{C^1_8*C_8^1}{C^2_{16}}=\frac{8}{15};\\P_4=\frac{C^1_7*C^1_7}{C^2_{14}}=\frac{7}{13};\\P_5=\frac{C^1_6*C^1_6}{C^2_{12}}=\frac{6}{11};\)
3) требуемая вероятность:
P=P₁*P₂*P₃*P₄*P₅≈0,04365.
From least to greatest, What are the x–coordinates of the three points where the graphs of the equations intersect? If approximate, enter values to the hundredths.
,
,
Answers
The x-coordinates where the graphs of the equations intersect are x = -1 and x = 3
How to determine the x-coordinates where the graphs of the equations intersect?From the question, we have the following parameters that can be used in our computation:
y = 2x
y = x² - 3
The x-coordinates where the graphs of the equations intersect is when both equations are equal
So, we have
x² - 3 = 2x
Rewrite the equation as
x² - 2x - 3 = 0
When the equation is factored, we have
(x + 1)(x - 3) = 0
So, we have
x = -1 and x = 3
Hence, the x-coordinates are x = -1 and x = 3
Read more about equations at
https://brainly.com/question/148035
#SPJ1
Question
From least to greatest, What are the x–coordinates of the three points where the graphs of the equations intersect? If approximate, enter values to the hundredths.
y = 2x
y = x² - 3
You have to conduct a survey in your school to find out which mode of transportation students prefer the most. Arrange the steps for comple
this project in order from start to finish.
Answers
Answer:
Here are the steps for conducting a survey in your school to find out which mode of transportation students prefer the most, arranged in order from start to finish:
1) Define the objective: Clearly define the objective of the survey, which is to determine the preferred mode of transportation among students in your school.
2) Determine the sample size: Decide on the number of students you want to include in your survey. This will depend on factors such as the size of your school and the resources available for conducting the survey.
3) Design the survey questionnaire: Create a well-designed survey questionnaire that includes relevant questions about different modes of transportation. Ensure that the questions are clear, unbiased, and cover all the necessary aspects.
4) Seek necessary permissions: If required, seek permission from school authorities or relevant individuals to conduct the survey on school premises and to involve students.
5) Pre-test the survey: Before distributing the survey to the entire student population, pre-test the questionnaire on a small group of students to identify any potential issues or areas for improvement.
6) Distribute the survey: Once the questionnaire has been finalized and pre-tested, distribute it to the selected sample of students. Ensure that the survey is distributed in a fair and unbiased manner, taking into account the diversity of the student population.
7) Collect the survey responses: Set a specific timeframe for students to complete the survey and collect the responses. Consider using a combination of online platforms and physical collection methods to maximize participation.
8) Analyze the data: Once you have collected all the survey responses, analyze the data to determine the preferred mode of transportation among students. Use appropriate statistical tools and techniques to interpret the results accurately.
9) Present the findings: Prepare a report or presentation summarizing the survey findings. Include key insights, trends, and any significant findings related to the preferred mode of transportation among students.
10) Share the results: Share the survey results with the school community, including students, teachers, and administrators. This can be done through presentations, newsletters, or other suitable communication channels.
By following these steps, you will be able to conduct a comprehensive survey to determine the preferred mode of transportation among students in your school.
Hope this helps!
I can not do it for you but I can give you what you should do
Explanation: take a survey
Hey, Can anyone assist me with a bunch of calculus questions, thank you in advance


Answers
Answer:
1. (a) [-1, ∞)
(b) (-∞, -1) ∪ (1, ∞)
2. (a) (1, 3)
(b) (-∞, 1) ∪ (3, ∞)
3. (a) 9.6 m and 0.4 m
(b) 03:08 and 15:42
Step-by-step explanation:
The domain of a function is the set of all possible input values (x-values).
The range of a function is the set of all possible output values (y-values).
Question 1Part (a)
When x < 0, the function is f(x) = x².
Since the square of any non-zero real number is always positive, the range of the function f(x) for x < 0 is (0, ∞).
When x ≥ 0, the function is f(x) = sin(x).
The minimum value of the sine function is -1 and the maximum value of the sine function is 1. As the sine function is periodic, the function oscillates between these values. Therefore, the range of function f(x) for x ≥ 0 is [-1, 1].
The range of function f(x) is the union of the ranges of the two separate parts of the function. Therefore, the range of f(x) is [-1, ∞).
Part (b)
The domain of the function g(x) = ln(x² - 1) is the set of all real numbers x for which (x² - 1) is positive, since the natural logarithm function (ln) is only defined for positive input values.
Find the values of x:
\(\implies x^2-1 > 0\)
\(\implies x^2 > 1\)
\(\implies x < -1, \;\;x > 1\)
Therefore, the domain of function g(x) is (-∞, -1) ∪ (1, ∞).
Question 2Part (a)
To determine the interval where f(x) < 0, we need to find the values of x for which the quadratic is less than zero.
First, set the function equal to zero and solve for x:
\(\begin{aligned} x^2-4x+3&=0\\x^2-3x-x+3&=0\\x(x-3)-1(x-3)&=0\\(x-1)(x-3)&=0\\ \implies x&=1,\;3\end{aligned}\)
Therefore, the function is equal to zero at x = 1 and x = 3 and so the parabola crosses the x-axis at x = 1 and x = 3.
As the leading coefficient of the quadratic is positive, the parabola opens upwards. Therefore, the values of x that make the function negative are between the zeros. So the interval where f(x) < 0 is 1 < x < 3 = (1, 3).
Part (b)
Since the square root of a negative number cannot be taken, and dividing a number by zero is undefined, function f(x) has to be positive and not equal to zero: f(x) > 0.
As the parabola opens upwards, the values of x that make the function positive are less than the zero at x = 1 and more than the zero at x = 3.
Therefore the domain of g(x) is (-∞, 1) ∪ (3, ∞).
Question 3Part (a)
The range of a sine function is [-1, 1]. Therefore, to calculate the maximal and minimal possible water depths of the bay, substitute the maximum and minimum values of sin(t/2) into the equation:
\(\textsf{Maximum}: \quad 5+4.6(1)=9.6\; \sf m\)
\(\textsf{Maximum}: \quad 5+4.6(-1)=0.4\; \sf m\)
Part (b)
To find the times when the depth is maximal, set sin(t/2) to 1 and solve for t:
\(\implies \sin \left(\dfrac{t}{2}\right)=1\)
\(\implies \dfrac{t}{2}=\dfrac{\pi}{2}+2\pi n\)
\(\implies t=\pi+4\pi n\)
Therefore, the values of t in the interval 0 ≤ t ≤ 24 are:
\(t = \pi=3.14159265...\sf hours\;after\;mindnight\)\(t=5 \pi = 15.7079632...\sf hours\;after\;mindnight\)Convert these values to times:
03:08 and 15:42Simplify.
2x-4
²-8+12
O
O
O
-6
x+6
x-6
-
x-2
²-82+12
Answers
The simplified value of (2x - 4)² is 4x² - 16x + 16.
First, let us understand the algebraic identities;
Algebraic identities are equations in which the left hand side of the equation is identically equal to the right hand side of the equation.
Some of the identities are:
(a + b)² = a² + 2ab + b²(a - b)² = a² - 2ab + b², etc.We are given (2x - 4)².
Use the identity (a - b)² = a² - 2ab + b² to expand to the given expression.
So, a = 2x and b = 4.
Put it into the identity, we will get;
Therefore,
(2x - 4)² = (2x)² - 2 * 2x * 4 + (4)² = 4x² - 16x + 16
Thus, the simplified value of (2x - 4)² is 4x² - 16x + 16.
To learn more about the algebraic identities visit:
https://brainly.com/question/16857438
#SPJ1
On the following unit circle, θ θtheta is in radians and tan ( θ ) = − 0.99 0.1 = − 9.9 tan(θ)= 0.1 −0.99 =−9.9tangent, left parenthesis, theta, right parenthesis, equals, start fraction, minus, 0, point, 99, divided by, 0, point, 1, end fraction, equals, minus, 9, point, 9. y y x x 1 1 − 1 −1 1 1 − 1 −1 θ θ ( 0.1 , − 0.99 ) (0.1,−0.99) A unit circle with an angle from the positive x-axis to a ray labeled theta. The point where the ray intersects the circle is labeled 0.1, negative 0.99 and is in the fourth quadrant. Without a calculator, evaluate the following expressions to the nearest

Answers
Answer: tan(pi+theta)=-9.9
Tan(2pi+theta)=-9.9
Step-by-step explanation:
By trigonometric expressions we conclude that the values of the tangent functions of the angles π + θ and 2π + θ radians are both equal to - 9.9.
How to calculate trigonometric functions from unit circle
A unit circle is a circle with a radius of a unit used to calculate the value of trigonometric functions associated to a right triangle. In this case, the tangent function for a point (x, y) is:
tan θ = y/x (1)
The trigonometric expression for the tangent of the sum of two angles:
\(\tan (\alpha + \theta) = \frac{\tan \alpha + \tan \theta}{1 - \tan \alpha \cdot \tan \theta}\) (2)
Now we proceed to calculate the trigonometric expressions:
\(\tan (\pi + \theta) = \frac{\frac{-0.99}{0.1}+0}{1-\left(\frac{-0.99}{0.1}\right)\cdot (0)}\)
\(\tan (\pi + \theta) = -9.9\)
\(\tan (2\pi + \theta) = \frac{\frac{-0.99}{0.1}+0}{1-\left(\frac{-0.99}{0.1}\right)\cdot (0)}\)
\(\tan (2\pi + \theta) = -9.9\)
By trigonometric expressions we conclude that the values of the tangent functions of the angles π + θ and 2π + θ radians are both equal to - 9.9.
To learn more on trigonometric expressions: https://brainly.com/question/6904750
#SPJ2
What is the length of EF in the right triangle below?
D
26
10
E
F
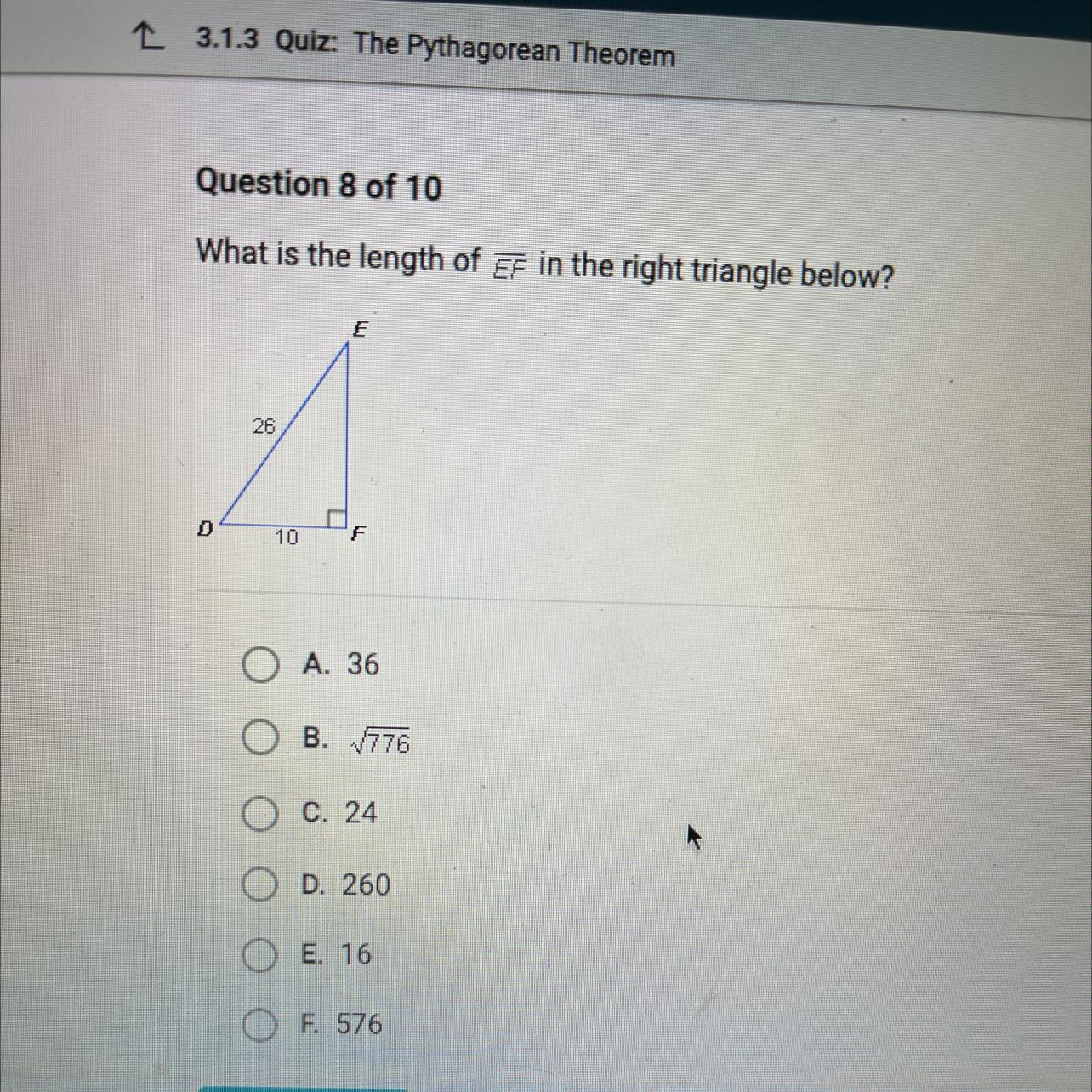
Answers
The measure of side length EF in the right triangle is 24.
What is the measure of side length EF?The Pythagorean theorem states that the "square on the hypotenuse of a right-angled triangle is equal in area to the sum of the squares on the other two sides.
It is expressed as;
c² = a² + b²
From the diagram:
Hypotenuse DE = c = 26
Leg DF = a = 10
Leg EF = b = ?
Plug in the values and solve for b:
c² = a² + b²
26² = 10² + b²
676 = 100 + b²
b² = 676 - 100
b² = 576
b = +√576 ( we take the positive value since we are dealing with dimensions)
b = 24
Therefore, the length EF is 24.
Option C)24 is the correct answer.
Learn more about Pythagorean theorem here: brainly.com/question/343682
#SPJ1
What is the surface area of the square pyramid? 6 square meters 16 square meters 28 square meters 49 square meters
Answers
Answer:
It's 16, i did the unit test already.
Step-by-step explanation:
He buys atoy car for 150 the sells it for $120find his percentage loss
Answers
Answer: 80%
Step-by-step explanation:
divide 120 by 150 and you get .8 then you move the decimal over 2
PLS HELP 20 points !!!

Answers
For the expression (3w²)/(w⁴) the simplified-value is 3/w², the correct option is (c).
The "Simplified-Expression" refers to an algebraic expression that has been reduced to its most basic and concise form, without changing the value of the expression.
The simplified expression is the most reduced-form, and it has the same value as the original expression.
We have to simplify the expression (3w²)/(w⁴),
We can rewrite w⁴ as (w²)², which means that we can cancel one of the w² terms in the numerator and denominator.
This gives us : (3w²)/(w⁴) = (3/1) × (w²/(w²)²) = 3/w²
Therefore, the simplified value of is (c) 3/w².
Learn more about Expression here
https://brainly.com/question/24020271
#SPJ1
In a marketing survey, a random sample of 1020 supermarket shoppers revealed that 268 always stock up on an item when they find that item at a real bargain price.
a. Find a 95% confidence interval for p?
b. What is the margin of error based on a 95% confidence interval?
Answers
Answer:
a) 95% of the confidence intervals created using this method would include the true proportion of shoppers who stock up on bargains.
b) Margin of error = 0.0270.
Step-by-step explanation:
a)
\(\hat{p}\) = point estimate of p \(= 268/1020 =0.2627\)
\(\hat{q}= 1 - 0.2627 = 0.7373\)
\(SE = \sqrt{\hat{p}\hat{q}/n}\\\\=\sqrt{0.2627\times 0.7373/1020}=0.0138\\\alpha = 0.05\)
From Table, critical values of \(Z= \pm1.96\) ,
Lower limit
\(= \hat{p} - Z SE\\ = 0.2627 - (1.96 X 0.0138) \\ = 0.2627 - 0.0276 \\ = 0.236\)
upper limit = 0.2627 + 0.0276
= 0.2903
Correct option:
95% of the confidence intervals created using this method would include the true proportion of shoppers who stock up on bargains.
b) Margin of error =Z SE
= 1.96 X 0.0141
= 0.0270.
Enter the unknown value that makes this statement true.
35 is % of 70
Answers
Answer:
Step-by-step explanation:
35 = x% of 70
35 = 1/2 of 70
x% = 50%
x = 50
For the real-valued functions f (x)=x² +4 and g(x)=x-5, find the composition f g and specify its domain using interval notation.0 0.0DOf(x) = 1

Answers
Ok, so
We got these two functions:
\(\begin{gathered} f(x)=x^2+4 \\ g(x)=x-5 \end{gathered}\)We're going to find the composition (f o g)(x).
This composition is the same that evaluate the function f(x) in g(x).
This is, f (g(x)):
\(\begin{gathered} f(x-5) \\ =(x-5)^2+4 \end{gathered}\)Simplifying:
\(\begin{gathered} =x^2-10x+25+4 \\ =x^2-10x+29 \end{gathered}\)As these two functions are polynomials, then, the domain of (fog)(x), will be:
\((-\infty,\infty)\)In the figure below, triangle ABC is similar to triangle PQR, as shown below:. PLEASE HELP ME!!!!!!!!!!

Answers
Answer:
35 i think
Step-by-step explanation:
If OQ and RT are parallel lines and mQPS = 136°
Answers
Angle QPS and angle RTS are congruent, both measuring 136°. Additionally, since OQ and RT are parallel, angle PSQ and angle RTS are alternate interior angles and are also congruent.
If OQ and RT are parallel lines and m QPS = 136°, we can use the property that when a transversal intersects two parallel lines, the corresponding angles are congruent.
Therefore, angle QPS and angle RTS are congruent, both measuring 136°. Additionally, since OQ and RT are parallel, angle PSQ and angle RTS are alternate interior angles and are also congruent.
Hence, angle PSQ measures 136° as well. In summary, angles QPS, PSQ, and RTS all have a measure of 136°.
This is because when two lines are parallel and intersected by a transversal, the corresponding angles and alternate interior angles are congruent.
For more such questions on congruent
https://brainly.com/question/29789999
#SPJ8
The complete question is given below:
If OQ and RT are parallel lines and m QPS = 136°
Andre's coin jar contains 85 cents. There are no quarters or pennies in the jar, so the jar has all nickels, all dimes, or some of each.
Let x' be the number of nickels and y be the number of dimes.
Which of the following equations represents this situation?
O x+y=85
Oy+x=85
0 5x+10y = 85
10x + 5y = 85

Answers
Answer:
C, 5x + 10y = 85
Step-by-step explanation:
There are 5 cents in a nickel, so that will be 5x because x will be the number of nickels as said earlier and 5 will be the nickel.
There is 10 cents in a dime, so that will be 10y because y will be the number of dimes used as mentioned, and 10 will be the dime.
Both of those added, (5x + 10) will have a result of 85.
That's why 5x + 10y = 85 would best be the appropriate equation to use here.
x+y=7 in slope intercept form
Answers
Answer:
y = -x + 7
Step-by-step explanation:
The slope formula is as follows:
y = mx + b
So, in order to get x + y = 7 into slope intercept form we have to do the following things:
Subtract x from both sidesIf you do this step then your equation should look like this:
y = -x + 7
Hope this helps!!
- Kay
Answer:
y = -x + 7
Step-by-step explanation:
Start with the givenx + y = 7
Use the Subtraction Property of Equality to isolate the y-variablex + y = 7
-x -x
Simplyy = -x + 7
How many solutions does the system of equations below have? y=-3/4x+1/6
Answers
The solution is the point (0, 1/6) y = 1/6
Given the equation y = (-3/4)x + 1/6, which represents a linear equation, there is no "system" of equations involved since there is only one equation.
In this case, the equation is in slope-intercept form (y = mx + b),
where m represents the slope (-3/4) and b represents the y-intercept (1/6).
The slope-intercept form allows us to determine various properties of the equation.
Since there is only one equation, the solution to this equation is a single point on the Cartesian plane.
Each pair of x and y values that satisfy the equation represents a solution.
For example, if we choose x = 0, we can substitute it into the equation to find the corresponding y value:
y = (-3/4)(0) + 1/6
y = 1/6
Therefore, the solution is the point (0, 1/6).
In summary, the given equation has a unique solution, represented by a single point on the Cartesian plane.
Any value of x plugged into the equation will yield a corresponding y value, resulting in a unique point that satisfies the equation.
For similar question on linear equations.
https://brainly.com/question/22688504
#SPJ8
A soccer league has $6,333 to buy new soccer balls. If each ball costs $3, how many balls can the league buy?
Answers
Answer: 2,111 soccer balls
Step-by-step explanation:
We will divide the total amount of money by the price per ball to find how many balls the league can buy.
$6,333 / $3 = 2,111
The league can buy 2,111 soccer balls.
An aircraft seam requires 29 rivets. The seam will have to be reworked if any of these rivets is defective. Suppose rivets are defective independently of one another, each with the same probability. (Round your answers to four decimal places.)
(a) If 17% of all seams need reworking, what is the probability that a rivet is defective?
(b) How small should the probability of a defective rivet be to ensure that only 5% of all seams need reworking?
Answers
The probability that a rivet is defective is 0.0247, and in ensuring that only 5% of all seams need reworking then the probability of a defective rivet is 0.0059.
Let p be the probability of a rivet being defective. The probability of a seam being defective is given by the binomial distribution:
P(defective) = 29Cx × p^x × (1-p)^(29-x)
where x is the number of defective rivets.
We know that 17% of seams are defective, so:
0.17 = ∑_{x=1}^{29} 29Cx × p^x × (1-p)^(29-x)
Solving for p, we have:
p = 0.0247
If only 5% of all seams need reworking, then:
0.05 = ∑_{x=1}^{29} 29Cx × p^x × (1-p)^(29-x)
Solving for p, we have:
p = 0.0059
To learn more about probability visit: https://brainly.com/question/13604758
#SPJ4
Question 1: What is the GCF of 10x2+15x?
10
5x2
10x2
5x
x
10x
5
Question 2: What is your answer to step 2, when factoring 10x2−15x?
picture attached
Question 2 options:
10x + 15
2x2−3x
2x - 3
2x + 3
10x-15
10x - 15x
Question3: Factor 10x2− 15x (hint step 3)

Answers
Answer:
694
Step-by-stp explanation:
Gator Brews manufactures three types of brews: A, B, and C. These brews are produced via twa production processes: 1 and 2. Running process 1 for an hour costs $400 and yields three hundred gallons of brew A, one hundred gallons of brew B, and one hundred gallons of brew C. Running process 2 for an hour costs $100 and yields one hundred gallons of brew A, one hundred gallons of brew B. To meet customer demands, at least 1000 gallons of brew A, 500 gallons of brew B, and 300 gallons of brew C must be produced daily. Gator Brews wants to minimize the cost of running both processes. Set up and answer this question in worksheet "Part 6" using the simplex method in solver. (15 points) X1-hrs of process 1 X2 - hrs of process 2 MIN Z = 400x1 +100X2 s.t. Gallons of A 300 x1 + 100 x2 1000 Gallons of B 100 x1 + 100 x2 2500 Gallons of C 100 x1 + 0x2 2 300
Answers
Answer:
z(min) = 1400
x = 3
y = 2
Step-by-step explanation:
Formulation:
Let´s call
x number of running hours of process 1
y number of running hours of process 2
Then Objective Function to minimize is:
z = 400*x + 100*y
Constrains:
Subject to
Demand constraint ( by type of brews)
300*x + 100y ≥ 1000
100*x + 100*y ≥ 500
100*x ≥ 300
General constraint
y≥0 Note that we already have x≥= (in the third constraint)
By using the on-line slver we find:
z (min) = 1400 $
x = 3
y = 2
QUESTION 4 PATTERNS, FUNCTIONS AND ALGEBRA 1. Given 6x³-8x³+2+9x7-4x a. How many terms are there in the polynomial? State the degree of the polynomial c. Determine the value of the polynomial if x=-1 b.
Answers
Answers:
a) There are 5 termsb) Degree = 7c) The value is -1==========================================
Explanation:
a) Each term is separated by a plus or a minus.b) The degree is equal to the largest exponent. This applies to single variable polynomials only.c) Replace each x with -1. Then use the order of operations PEMDAS to simplify. You should get -1 as the answer. Use a calculator to confirm. It is a coincidence that we have the same input and output. This will not always happen with any general polynomial function.