The following 10 scores were input in the gradebook for Prof. Thompson's class.74, 75, 78, 79, 80, 81, 82, 84, 84, 87Identify all values that are outliers.
Answers
To identify the ouliers we can use the Interquartile Range (IQR).
1. To find the IQR, we need to have the data set in order:
74, 75, 78, 79, 80, 81, 82, 84, 84, 87.
2. Find the median:
As we have an even set of numbers, just place a mark in the center of the data set:
74, 75, 78, 79, 80 | 81, 82, 84, 84, 87
3. Place parentheses around the numbers above and below the mark we just made:
(74, 75, 78, 79, 80) | (81, 82, 84, 84, 87)
4. Find the median in each group, it would be Q1 and Q3:
(74, 75, 78, 79, 80) | (81, 82, 84, 84, 87)
Q1=78 and Q3=84
5. Subtract Q1 from Q3:
Q3-Q1=84-78=6
This is the IQR: 6.
6. Multiply the IQR by 1.5:
IQR*1.5 = 6*1.5 = 9
7. Subtract this value from Q1:
Q1-9= 78-9 = 69 This is the lower limit
8. Add the value to Q3:
Q3+9= 84+9 = 93 This is the upper limit
Identify the numbers that are under the lower limit and above the upper limit, those are the outliers.
As you can see, in the data set there are not outliers.
Related Questions
Help plsssssssssssssssssssssss

Answers
Answer:
He rode his bike\(\frac{36}{5}\) mi
Step-by-step explanation:
\(\frac{7}{4}\) x \(\frac{4}{5}\) Simplify
7 x \(\frac{1}{5}\) = \(\frac{36}{5}\)
Answer:7/6
Step-by-step explanation:7/8 * 4/3=1 1/6 Simplest form would be 7/6
Chloe reads 7 pages of a mystery book in 9 minutes. What is her average reading rate in pages per
minute?
Answers
Answer:
1.25
Step-by-step explanation:
you have to take the 9 pages and divide by 7 and then divide that by 60 and u get 1.25
Sam's dad gave him $30 for washing their car. He used the money to buy a basketball for $7.50 and three sports drinks for $2.75 each, Sam also bought a bag
of candy
if Sam went home with 1/3 of the money his dad gave him how much did the bag of candy cost?
Answers
Answer:
4.25 $
Step-by-step explanation:
2.75 × 3 = 8.25
8.25 + 7.50 = 15. 75
30 - 17.75 = 14.25
14.25 - 10 = 4.25
The bag of candy costs $4.25
The sum of the lengths of KLM is 24.62 cm. The length of KL is 3 cm and the length of LM is 17.8 cm. What is the length of KM and what kind of triangle is this?
Answers
Answer:
The Answer Is A/3.82
Step-by-step explanation:
i got it by subtracting the sum of 3 and 17.8 off 24.62. Hope this helps!
i need help with this one plz! (marking BRAINLIST) :)

Answers
Answer:
Sinx = c/b
cosx = a/b
tanx = c/a
Step-by-step explanation:
B is hypotenuse, a is adjacent, c is opposite of angle x.
Sin = opposite/hypotenuse
cos = adjacent/hypotenuse
tan = opposite/adjacent
The ratio of the number of students to the number of parking spaces on a college campus is 4:1. Which expression could be used to find the number of parking spaces on the campus if there are 2,240 students?
Answers
Answer:
4/1 = 2240/x
Step-by-step explanation:
students : parking spaces = 4 : 1
4/1 = 2240/x
Answer:
4/1 = 2240/x
Step-by-step explanation:
pls tell me if wrong have a good day/night<3
Which statement BEST expresses a connection between gravity and friction? A. Gravity and friction work together to provide the strong, opposing force that slows a snowboarder's ride. B. Gravity and friction are connected as they are the only two factors influencing speed when snowboarding. C. Gravity and friction are opposing forces; gravity holds a snowboarder in place while friction pulls a snowboarder down. D. Gravity and friction result in successful snowboarding after the transference of gravity into energy and a lubricating water layer produced by friction.
Answers
Answer:
D
Step-by-step explanation:
I had this question on a test and D was right
it's worded the exact same way
Answer:
a.
providing a force to propel the snowboarder down a slope to gain speed
The guy above me is a fool
Step-by-step explanation:
You want to take out a $219,000 mortgage (home loan). The interest rate on the loan is 4.5%, and the loan is for 30 years. Your monthly payments are $1,109.64. How much will still be owed after making payments for 15 years? Round your answer to the nearest dollar.
Answers
After making payments for 15 years, the amount still owed on the mortgage would be approximately $145052.36.
To determine how much will still be owed after making payments for 15 years, we can use the formula for the remaining balance on a mortgage:
Remaining balance = P ((1 + r)ⁿ - (1 + r)ᵇ) / ((1 + r)ⁿ - 1)
where:
P = the initial loan amount (in this case, $219,000)
r = the monthly interest rate (which is the annual interest rate divided by 12)
n = the total number of monthly payments (which is 30 years times 12 months per year, or 360 months)
b = the number of monthly payments made so far (which is 15 years times 12 months per year, or 180 months)
First, we need to calculate the monthly interest rate:
r = 4.5% / 12 = 0.00375 = 0.375%
Next, we can plug in the values to get:
Remaining balance = $219,000 ((1 + 0.00375)³⁶⁰- (1 + 0.00375)¹⁸⁰) / ((1 + 0.00375)³⁶⁰ - 1)
= $145052.36
To learn more about loan calculations;
https://brainly.com/question/28244942
#SPJ1
Translate the sentence into an equation. The sum of 2 times a number and 3 is 9. Use the variable b for the unknown number.
Answers
Answer:
Answer: 2b+3 = 7
=================================================
Work Shown:
b = unknown number
2b = 2 times a number
2b+3 = the sum of 2 times a number and 3
2b+3 = 7, since the expression above is set equal to 7
Step-by-step explanation:
A cannonball is fired in the air at an angle of 45°. How far does it travel before it is 600 feet above ground? (Assume the cannonball travels in a straight line. Ignore the force of gravity and wind resistance. Round your answer to the nearest foot.)
Answers
Answer:
Step-by-step explanation:
Since the cannonball is fired at an angle of 45°, it will have the same horizontal and vertical velocities.
Let x be the distance it travels before it is 600 feet above ground. At this point, its vertical displacement will be 600 feet, and we can use the formula for vertical displacement:
y = v0*t + (1/2)at^2
Since there is no initial vertical velocity and we are ignoring gravity, a = 0 and the equation simplifies to:
y = 0*t + 0 = 600
Solving for t, we get:
t = sqrt(2y/a) = sqrt(2*600/0) = undefined
This means that the cannonball will never be 600 feet above ground if we ignore gravity. Since this is not realistic, we cannot answer this question without additional information or by assuming that gravity is acting on the cannonball.
There is a 30 percent chance that A can fix her busted computer. If A cannot, then there is a 40 percent chance that her friend B can fix it.
a) Find the probability it will be fixed by either A or B.
b) If it is fixed, what is the probability it will be fixed by B.
Answers
a) The probability that the computer will be fixed by either A or B is 58%.
b) The probability that it was fixed by B is 57.14%
Given data:
a)
To find the probability that the computer will be fixed by either A or B, we can use the principle of addition for probabilities.
The probability that A can fix the computer is 30% or 0.30, and the probability that B can fix the computer if A cannot is 40% or 0.40.
Therefore, the probability that either A or B can fix the computer is the sum of these probabilities:
P(A or B) = P(A) + P(B if A cannot) = 0.30 + (0.70 * 0.40) = 0.30 + 0.28 = 0.58
Therefore, there is a 58% probability that the computer will be fixed by either A or B.
b)
Let's denote event A as A fixing the computer and event B as B fixing the computer.
P(A) = 0.30 (probability A can fix the computer)
P(B|A') = 0.40 (probability B can fix the computer given that A cannot)
To find P(B|A), the probability that B fixes the computer given that it was fixed, use Bayes' theorem:
P(B|A) = (P(A|B) * P(B)) / P(A)
Since the computer is fixed, P(A) + P(A') = 1, so P(A) = 1 - P(A') = 1 - 0.30 = 0.70
P(B|A) = (P(A|B) * P(B)) / P(A)
P(B|A) = (1 * 0.40) / 0.70
P(B|A) = 0.40 / 0.70
P(B|A) ≈ 0.5714
Hence, if the computer is fixed, there is a 57.14% probability that it was fixed by B.
To learn more about Bayes's theorem, refer:
https://brainly.com/question/29598596
#SPJ4
Question #3
Given the following stemplot, determine the maximum value of the original data set.
O 100
8
98
9
0000
Test Scores
5
479
6 146779
7 002557799
8 12223455789
9 000333368
Answers
The maximum value of the original data set is 109.
To determine the maximum value of the original data set from the given stemplot, we need to look at the rightmost digits in each stem and identify the highest value.
Looking at the stemplot:
O 10 | 0 0 8 9 8 9 0 0 0
0 20 | 5 4 7 9 6
0 30 | 1 4 6 7 7 9 7
0 40 | 0 0 2 5 5 7 7 9 9 8
0 50 | 1 2 2 2 3 4 5 5 7 8 9 9
0 60 | 0 0 0 3 3 3 3 6 8
The rightmost digits in each stem represent the original data values. We can see that the highest value occurs in the stem "10" with a rightmost digit of "9".
Therefore, the maximum value of the original data set is 109.
For such more question on value:
https://brainly.com/question/843074
#SPJ8
A bagel shop sells coffee in a container shaped like a rectangular prism. A graphic designer who works for the bagel shop drew the net below to create a design for the container.
Answers
1598 cm square is the area of the container.
According to the statement
we have given that the container is rectangular prism
And Length of rectangular prism is 34cm
Width of rectangular prism is 17 cm
Height of rectangular prism is 20 cm
we use the below written formula to find the surface area
Surface area formula A=(wl+hl+hw)
To find the surface area of the container.
Substitute the values of Length, width and height in the formula then
A=(wl+hl+hw)
A=((17)(34)+(20)(34)+(20)(17))
After solving the values
A=(578+680+340)
A= 1598
So, 1598 cm square is the area of the container.
Learn more about AREA here https://brainly.com/question/6613758
#SPJ1
Solve the following inequality algebraically. |x – 5| =< 8
Answers
l x -5 l ≤ 8
There are two results:
x-5 ≤ 8 and x-5 ≥ -8
Solve each inequality
x-5 ≤ 8
x ≤ 8+5
x≤ 13
x-5 ≥ -8
x ≥ -8+5
x ≥ -3
Solution:
-3 ≤ x ≤ 13
solve only number 6

Answers
To find the tangent line of the graph:
⇒ must find:
point at which the tangent line touches the graphslope of the tangent lineLet's find the point at which the tangent line touches the graph:
At x = -1,
\(y = ((-1)^3+2)^5=(-1+2)^5=1^5=1\)
Point: (-1,1)
Let's find the slope of the tangent line
⇒ get the derivation of function than plug (-1) in the x-position to get
the exact slope
\(\frac{d}{dx}(x^3+2)^5=5(x^3+2)^4*\frac{d}{dx}(x^3+2)=5(x^3+2)^4*3x^2\\ \\ 5((-1)^3)+2)^4*3(-1)^2=5(-1+2)^4*3*1=5*(1)^4*3=5*1*3=15\)
Slope of tangent line: 15
Now put all the calculated value into the point-slope form:
\((y-y_{0})=m(x-x_{0} )\)
\((x_{0} ,y_{0} )\) --> point on the tangent linem --> tangent slope's valueSo:
\((y-1)=15(x+1)\\y - 1= 15x + 15\\y = 15x + 15 + 1\\y = 15x + 16\)
Thus the tangent line's equation is y = 15x + 16
Answer: y = 15x + 16
Hope that helps!
Find the probability of no successes in six trials of a binomial experiment in which the probability of success is 30%.
Answers
Answer: 0.02655
Step-by-step explanation:
Explanation: The formula for finding the probability of no successes in a binomial experiment is given by (1 - p)^n, where p is the probability of success in a single trial and n is the number of trials. In this case, p = 0.30 and n = 6. So, the probability of no successes is (1 - 0.30)^6 = 0.02655.
3=5/(2-X), solve for x
Answers
The solution for x in the equation 3 = 5/(2 - x) is 11/3
How to determine the solution for x in the equationFrom the question, we have the following parameters that can be used in our computation:
3 = 5/(2 - x)
Cross multiply the equation
so, we have the following representation
3(2 - x) = 5
This gives
2 - x = 5/3
So, we have
x = 2 + 5/3
Evaluate the sum of the like terms
x = 11/3
Hence, the solution for x in the equation is 11/3
Read more about equation at
https://brainly.com/question/148035
#SPJ1
A ladder of length (2x+6) feet is positioned x feet from a wall. If the ladder reaches a height of (2x+4) feet along the wall. Find the longest leg.
A. 10ft
B. 24ft
C. 26ft
D. 13cm
Answers
Using the Pythagoras theorem, the longest leg has the length of 24 feet.
Given that,
A ladder of length (2x+6) feet is positioned x feet from a wall.
Height of the ladder = (2x + 6) feet
Distance of ladder from the wall = x feet
Height of the wall that the ladder is placed = (2x + 4) feet
These three lengths form s right triangle where (2x + 6) feet is the hypotenuse.
Longest leg is (2x + 4) feet
Using the Pythagoras theorem,
(2x + 6)² = (2x + 4)² + x²
4x² + 24x + 36 = 4x² + 16x + 16 + x²
4x² + 24x + 36 = 5x² + 16x + 16
x² - 8x - 20 = 0
(x - 10) (x + 2) = 0
x = 10 or x = -2
x = 2 is not possible.
So x = 10
Longest leg = 2x + 4 = 20 + 4 = 24 feet
Hence the length of the longest leg is 24 feet.
Learn more about Pythagoras theorem here :
https://brainly.com/question/343682
#SPJ1
center (-4, -7), tangent to x = 2
Answers
Answer:
(x + 4)^2 + (y + 7)^2 = 36
Step-by-step explanation:
The given information describes a circle with its center at (-4, -7) and tangent to the vertical line x = 2. To determine the radius of the circle, we need to find the distance between the center and the tangent line.
The distance between a point (x1, y1) and a line Ax + By + C = 0 is given by:
d = |Ax1 + By1 + C| / sqrt(A^2 + B^2)
In this case, the equation of the line is x = 2, which can be written as 1x + 0y - 2 = 0. Therefore, A = 1, B = 0, and C = -2. The center of the circle is (-4, -7), so x1 = -4 and y1 = -7. Substituting these values into the formula, we get:
d = |1*(-4) + 0*(-7) - 2| / sqrt(1^2 + 0^2)
d = |-6| / sqrt(1)
d = 6
Therefore, the radius of the circle is 6 units. The equation of a circle with center (h,k) and radius r is given by:
(x - h)^2 + (y - k)^2 = r^2
Substituting the values we have found, we get:
(x + 4)^2 + (y + 7)^2 = 36
This is the equation of the circle that satisfies the given conditions.
Sunset Lake is stocked with 2800 rainbow trout and after 1 year the population has grown to 7000. Assuming logistic growth with a carrying capacity of 28000, find the growth constant kk, and determine when the population will increase to 14600.
Answers
The growth constant is 1.0986 and the trout population will increase to 14600 after 2.1 years. The result is obtained by using the logistic equation.
How to find the increase of population?The increase of population can be found by using the logistic equation. It is
\(P(t) = \frac{K}{1 + Ae^{-kt} }\)
Where
P(t) = population at time t (in years)K = carrying capacityA = (K- P₀)/P₀k = growth constant of proportionalityt = time (in years)Sunset Lake is stocked with the rainbow trout. We have
P₀ = 2800P(1) = 7000K = 28000Find the growth constant k and time t when P(t) = 14600!
A = (K - P₀)/P₀
A = (28000 - 2800)/2800
A = 25200/2800
A = 9
After 1 year, we have 7000 rainbow trout. The growth constant is
\(7000 = \frac{28000}{1 + 9e^{-k(1)} }\)
\(1 + 9e^{-k} = 4\)
\(9e^{-k} = 3\)
\(e^{-k} = \frac{1}{3}\)
k = - ln (1/3)
k = 1.0986
Use k value to find the time when the population will increase to 14600!
\(14600 = \frac{28000}{1 + 9e^{-1.0986t} }\)
\(1.9178 = 1 + 9e^{-1.0986t}\)
\(0.9178 = 9e^{-1.0986t}\)
\(\frac{0.9178 }{9} = e^{-1.0986t}\)
\(t = \frac{ln \: 0.10198}{-1.0986}\)
t = 2.078
t ≈ 2.1 years
It is in another 1.1 years after t = 1.
Hence, the growth constant k is 1.0986 the population will increase to 14600 when t is 2.1 years.
Learn more about increase of population here:
brainly.com/question/13060148
#SPJ4
1/2-1/6
Jzjzhhzhzhzhhz
Answers
Answer:
ummm the answer is very simple
The answer is 0/6
Step-by-step explanation:
\( \frac{1}{2 \times 3} - \frac{1}{6} \)
\( \frac{1}{6} - \frac{1}{6} \)
\(1 - 1 = \frac{0}{6} \)
Find the length of the hypotenuse. Round your answer to the nearest tenth if necessary.
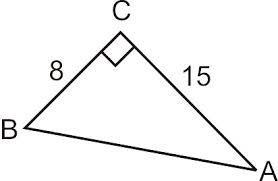
Answers
Answer:
a^2 + b^2 = c^2
8^2 + 15^2 = c^2
64 + 225 = c^2
289 = c^2
17 = c
The hypotenuse is 17.
Brainliest? ;)
Solve for x and show steps . Is the solution extraneous ? Check your work to show how you determined if the solution is extraneous or not
Square 4x-3=5
Answers
The solution of the equation 4x - 3 = 5 is not extraneous .
How to solve an equation?Extraneous solutions are values that we get when solving equations that aren't really solutions to the equation.
Therefore, let's solve the equation to know whether it is extraneous solution.
Hence,
4x - 3 = 5
add 3 to both sides of the equation
4x - 3 + 3 = 5 + 3
4x = 8
divide both sides of the equation by 4
4x / 4 = 8 / 4
x = 2
Therefore, it is not extraneous solution.
learn more on equation here: https://brainly.com/question/29135995
#SPJ1
Select the correct answer from each drop-down menu. The inequality 5m − 7 > 16 holds true for all numbers _ than _ in the set {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}.
Answers
The values of {m} that is greater than 4.6 represent the solution of the given inequality.
An inequality is used to compare two or more expressions or numbers.
For example -
2x > 4y + 3
x + y > 3
x - y < 6
The given inequality is -
5m - 7 > 16
Adding 7 on both sides, we get -
5m - 7 + 7 > 16 + 7
5m > 23
m > 23/5
m > 4.6
Therefore, the values of {m} that is greater than 4.6 represent the solution of the given inequality.
To solve more questions on inequality, visit the link-
brainly.com/question/11897796
#SPJ1
two stores sell cds in packages, as shown in the table below.

Answers
Answer:
Store A is 2 dollars greater than store B
Step-by-step explanation:
Store A Store B
1 : 0.70 1 : 0.60
20 : 14 20: 12
Hope that helps!
Compare the best estimate for 1.789/178 and 0.05. Which is less?
Answers
Answer:
The smaller number in 0.01
Step-by-step explanation:
To find this answer, just take the fraction and find the quotient of both numbers.
1.789/178 = 0.01005056179
Now take the quotient and compare it to 0.05.
Is 0.01 larger or 0.05 - the answer is 0.01.
85% of x is 51. Write an equation that represents the situation.
Answers
Answer:
85/100*x=51
Step-by-step explanation:
85x=5100
Carolyn was asked to solve the following system of equations. Her work is shown.
What error did Carolyn make? Identify her mistake and explain the error.

Answers
The mistake is on the second line of her work.
She wrote -2x + 4 when it should have been -2x -4 because she multiplied -2 by 2 the 4 would be negative: -2 x 2 = -4
Then adding 4 to the 7, x would be 11
Answer: She’s wrong because on the second line, she should’ve put -2x-4 instead of -2x+4 . X equals 11 because if you add 4 to 7 that’s what you’ll get ,
Step-by-step explanation:
To purchase 12,100 worth of machinery for her business, Latoya made a down payment of 1800 and took a business loan for the rest. After 3 years of paying monthly payments of 313.36, she finally paid off the loan.
A, what was the total amount latoya ended up paying for the machinery. (including down payment and monthly payments)
B. How much interest did latoya pay on the loan
Answers
The total amount that Latoya ended up paying for the machinery, was $ 13, 080 .96
The amount of interest that Latoya paid was $ 980.96
How to find the total amount paid ?The total amount paid by Latoya for the machinery can be found as :
= Down payment of the machinery + ( Monthly payments x Number of months per year x Number of years )
= 1, 800 + ( 313. 36 x 12 x 3 )
= $ 13, 080 .96
The total interest paid on the loan was :
= ( Monthly payments x Number of months per year x Number of years ) - Worth of the machine - down payment
= ( 313. 36 x 12 x 3 ) - 12, 100 - 1, 800
= $ 980.96
Find out more on total interest at https://brainly.com/question/14419626
#SPJ1
What is the answer pleaseee

Answers
The cross-sectional area of the cylinder with a base diameter of 44cm is approximately 1520.5 cm².
What is the cross-sectional area of the cylinder?A cylinder is simply a 3-dimensional shape having two parallel circular bases joined by a curved surface.
The cross-sectional area of a cylinder is expressed as;
Cross-sectional area A = πr²
From the diagram:
The dameter of the base of the base of the cylinder is 44cm.
We can determine the radius by dividing the diameter by 2:
Radius r = 44 cm / 2
Radius r = 22 cm
Now, plug the value of the radius into the formula to find the cross-sectional area:
Cross-sectional area A = πr²
Cross-sectional area A = π(22 cm)²
Cross-sectional area A = 484π cm²
Cross-sectional area = 1520.5 cm²
Therefore, the cross-sectional area is approximately 1520.5 cm².
Learn about volume of cylinder here: brainly.com/question/16788902
#SPJ1