The phone company NextFell has a monthly cellular plan where a customer pays a flat monthly fee and then a certain amount of money per minute used on the phone.

Answers
a. Since the cost, in dollars, is 47 for 260 minutes, we have:
\(\begin{gathered} y=mx+b \\ 47=260m+b \end{gathered}\)Also, since the cost, in dollars, is 108 for 870 minutes, we have:
\(108=870m+b\)Now, subtracting the first equation from the second, we obtain:
\(\begin{gathered} 108-47=870m+b-260m-b \\ \\ 61=610m \\ \\ m=\frac{61}{610} \\ \\ m=0.1 \end{gathered}\)Now, we can use this result to find the value of b:
\(\begin{gathered} 108=870\cdot0.1+b \\ \\ b=108-87 \\ \\ b=21 \end{gathered}\)Therefore, the equation is:
\(y=\mathbf{0.1x+21}\)b. Now, we need to find y for x = 894. We have:
\(\begin{gathered} y=0.1\cdot894+21 \\ \\ y=89.4+21 \\ \\ y=110.4 \end{gathered}\)Thus, the answer is:
If 894 minutes are used, the total cost will be 110.4 dollars.
Related Questions
ON A COMPUTER SCREEN ANSWER ASAP
Point M is drawn as the midpoint of BC.
Which of the following could be used as part of the proof that B2C? Select three that apply.
AB AC because of the definition of an isosceles triangle
BAC because corresponding parts of congruent triangles are congruent.
AABM 4 AACM because of the SAS triangle congruence criterion
BMCM because of the definition of a midpoint
AM A AM because of the Symmetric Property
Answers
Answer:
A. AB = AC because of the definition of an isosceles triangle
B. ∠B = ∠C because corresponding parts of congruent triangles are congruent.
D. BM = CM because of the definition of a midpoint
Step-by-step explanation:
A. An isosceles triangle is a triangle with two equal sides, hence:
AB = AC because of the definition of an isosceles triangle. option A is correct.
D. Since Point M is drawn as the midpoint of BC, hence:
BM = CM because of the definition of a midpoint. Option D is correct.
E. Reflexive property of congruence states that an angle, line segment, or shape is always congruent to itself. hence AM ≈ AM because of reflexive property.
AM ≈ AM because of the Symmetric Property is wrong. Option E is wrong.
C) The side - side - side (SSS) triangle congruence theorem states that if all the sides of two triangles are equal, then they are congruent triangles.
Since BM = CM, AM = AM and AB = AC, hence ΔABM = ΔACM because of the SSS triangle congruence criterion
ΔABM = ΔACM because of the SAS triangle congruence criterion is wrong. Option C is wrong.
D. Corresponding parts of congruent triangles are congruent. hence:
∠B = ∠C because corresponding parts of congruent triangles are congruent. Option B is correct

look at pic 10 pts will mark brainilest

Answers
Answer:
B
Step-by-step explanation:
Please awnser asap I will brainlist

Answers
They can buy 120 vans, 60 small trucks, and 80 large trucks.
How to find the number of van, small trucks and large truck needed?The truck company plans to spend 10 million on 260 vehicles. Each commercial van cost 25,000 dollars. Each small truck 50,000 dollars and each large truck 50,000 dollars. They needed twice as many van as small truck
Therefore,
let
s = number of small truck
number of van = v
let
l = number of large truck
v + s + l = 260
25,000(v) + 50,000(s) + 50,000(l) = 10,000, 000
v + 2s + 2l = 400
Hence,
v = 2s
So,
2s + 2s + 2l = 400
4s + 2l = 400
2s + s + l = 260
3s + l = 260
2s + l = 200
s = 60
l = 200 - 2(60)
l = 200 - 120
l = 80
v = 2(600 = 120
Therefore, they can buy the following:
number of small truck = 60
number of van = 120
number of large truck = 80
learn more on cost here: brainly.com/question/27903912
#SPJ1
Non Shaded Shaded
Area
Area
8
Find the radius
of the small circle

Answers
Answer:
The answer is 16pi or 50.3cm² to 1 d.p
Step-by-step explanation:
The non shaded=area of shaded
d=8
r=d/2=4
A=pir³
A=p1×4²
A=pi×16
A=16picm² or 50.3cm² to 1d.p
Answer:
3.45 cm (3 s.f.)
Step-by-step explanation:
We have been given a 5-sided regular polygon inside a circumcircle. A circumcircle is a circle that passes through all the vertices of a given polygon. Therefore, the radius of the circumcircle is also the radius of the polygon.
To find the radius of a regular polygon given its side length, we can use this formula:
\(\boxed{\begin{minipage}{6 cm}\underline{Radius of a regular polygon}\\\\$r=\dfrac{s}{2\sin\left(\dfrac{180^{\circ}}{n}\right)}$\\\\\\where:\\\phantom{ww}$\bullet$ $r$ is the radius.\\ \phantom{ww}$\bullet$ $s$ is the side length.\\\phantom{ww}$\bullet$ $n$ is the number of sides.\\\end{minipage}}\)
Substitute the given side length, s = 8 cm, and the number of sides of the polygon, n = 5, into the radius formula to find an expression for the radius of the polygon (and circumcircle):
\(\begin{aligned}\implies r&=\dfrac{8}{2\sin\left(\dfrac{180^{\circ}}{5}\right)}\\\\ &=\dfrac{4}{\sin\left(36^{\circ}\right)}\\\\ \end{aligned}\)
The formulas for the area of a regular polygon and the area of a circle given their radii are:
\(\boxed{\begin{minipage}{6 cm}\underline{Area of a regular polygon}\\\\$A=\dfrac{nr^2\sin\left(\dfrac{360^{\circ}}{n}\right)}{2}$\\\\\\where:\\\phantom{ww}$\bullet$ $A$ is the area.\\\phantom{ww}$\bullet$ $r$ is the radius.\\ \phantom{ww}$\bullet$ $n$ is the number of sides.\\\end{minipage}}\)
\(\boxed{\begin{minipage}{6 cm}\underline{Area of a circle}\\\\$A=\pi r^2$\\\\where:\\\phantom{ww}$\bullet$ $A$ is the area.\\\phantom{ww}$\bullet$ $r$ is the radius.\\\end{minipage}}\)
Therefore, the area of the regular pentagon is:
\(\begin{aligned}\textsf{Area of polygon}&=\dfrac{5 \cdot \left(\dfrac{4}{\sin\left(36^{\circ}\right)}\right)^2\sin\left(\dfrac{360^{\circ}}{5}\right)}{2}\\\\&=\dfrac{5 \cdot \left(\dfrac{4}{\sin\left(36^{\circ}\right)}\right)^2\sin\left(72^{\circ}\right)}{2}\\\\&=\dfrac{\dfrac{80\sin\left(72^{\circ}\right)}{\sin^2\left(36^{\circ}\right)}}{2}\\\\&=\dfrac{40\sin\left(72^{\circ}\right)}{\sin^2\left(36^{\circ}\right)}\\\\&=110.110553...\; \sf cm^2\end{aligned}\)
The area of the circumcircle is:
\(\begin{aligned}\textsf{Area of circumcircle}&=\pi \left(\dfrac{4}{\sin\left(36^{\circ}\right)}\right)^2\\\\&=\dfrac{16\pi}{\sin^2\left(36^{\circ}\right)}\\\\&=145.489779...\; \sf cm^2\end{aligned}\)
The area of the shaded area is the area of the circumcircle less the area of the regular pentagon plus the area of the small central circle.
The area of the unshaded area is the area of the regular pentagon less the area of the small central circle.
Given the shaded area is equal to the unshaded area:
\(\begin{aligned}\textsf{Shaded area}&=\textsf{Unshaded area}\\\\\sf Area_{circumcircle}-Area_{polygon}+Area_{circle}&=\sf Area_{polygon}-Area_{circle}\\\\\sf 2\cdot Area_{circle}&=\sf 2\cdot Area_{polygon}-Area_{circumcircle}\\\\2\pi r^2&=2 \cdot \dfrac{40\sin\left(72^{\circ}\right)}{\sin^2\left(36^{\circ}\right)}-\dfrac{16\pi}{\sin^2\left(36^{\circ}\right)}\\\\2\pi r^2&=\dfrac{80\sin\left(72^{\circ}\right)}{\sin^2\left(36^{\circ}\right)}-\dfrac{16\pi}{\sin^2\left(36^{\circ}\right)}\\\\\end{aligned}\)
\(\begin{aligned}2\pi r^2&=\dfrac{80\sin\left(72^{\circ}\right)-16\pi}{\sin^2\left(36^{\circ}\right)}\\\\r^2&=\dfrac{40\sin\left(72^{\circ}\right)-8\pi}{\pi \sin^2\left(36^{\circ}\right)}\\\\r&=\sqrt{\dfrac{40\sin\left(72^{\circ}\right)-8\pi}{\pi \sin^2\left(36^{\circ}\right)}}\\\\r&=3.44874763...\sf cm\end{aligned}\)
Therefore, the radius of the small circle is 3.45 cm (3 s.f.).

2(−6.4 + w) = 33.46
I NEED THIS ANSWER FAST
Answers
Answer:
W=23.13
Step-by-step explanation:
2(−6.4 + w) = 33.46
divide both sides
-6.4+w=16.73
move the constant to the right
w=16.73+6.4
end result-
w=23.13
Answer:
answer is 23.13
write an exponential model given two points:
(10, 140) and (11,220)
Answers
Hey guys I need help
-2z-xy=x+7 solve for x
If you could show the steps that’ll be awesome.
Answers
Answer:
\(x = -\frac{7 + 2z}{(y + 1)}\)
Step-by-step explanation:
-2z - xy = x + 7
Add 2z to both sides:
-2z + 2z - xy = x + 7 + 2z
-xy = x + 7 + 2z
Next, subtract x from both sides:
-xy - x = x - x + 7 + 2z
- xy - x = 7 + 2z
Factor out -x from the left-hand side of the equation:
- x(y + 1) = 7 + 2z
Divide both sides by - (y + 1) to isolate x:
\(\frac{x(y + 1)}{- (y + 1)} = \frac{7 + 2z}{-(y + 1)}\)
\(x = -\frac{7 + 2z}{(y + 1)}\)
Please mark my answers as the Brainliest, if you find this helpful :)
Please help with my exit ticket

Answers
9514 1404 393
Answer:
A. 2,144.66 in³
Step-by-step explanation:
The formula for the volume of a sphere is ...
V = (4/3)πr³
The radius is half the diameter, so this can be written in terms of diameter as ...
V = (4/3)π(d/2)² = (π/6)d³
For a diameter of 16 inches, the volume is ...
V = (π/6)(16 in)³ ≈ 2,144.66 in³
A local recreation center offers a yearly membership for $265. The center offers
aerobics classes for an additional $5 per class.
a. Write an equation that represents the total cost of the membership. (Suppose that y is the total cost and x the the number of classes)
b. Carly spent $500 one year. How many aerobics classes did she take?
Answers
Answer:
a. y = 265 + 5x
b. 500 = 265 + 5x
5x = 500 - 265
5x = 235
x = 235/5
x = 47
She took 47 aerobic classes.
Step-by-step explanation:
Total Cost is yearly cost + 5 into however many aerobic classes you take.
Find the number of classes by substituting values in the equation.
PLEASE HELP IMAGE ATTACHED!

Answers
The value of the determinants are
D=13
Dx =26
Dy =52
Dz =26
What is determinant?
The determinant of a matrix is a scalar value calculated for a given square matrix. Linear algebra deals with the determinant, it is calculated using the elements of a square matrix. It can be thought of as a scaling factor for the matrix transformation. Useful for solving a system of linear equations, calculating the inverse of a matrix, and numerical operations.
Given system is
x+ y-z= 4
3x+4y-3z=16
9x- 3y+4z=14
from the system the determinants become,
D= 1 1 -1
3 4 -3
9 -3 4
D= 1(16-9)-1(12+27)-1(-9-36)
=7-39+45
13
Dx=4 1 -1
16 4 -3
14 -3 4
=26
Dy=1 4 -1
3 16 -3
9 14 4
=52
Dz=1 1 4
3 4 16
9 -3 14
=26
Hence, D=13, Dx=26, Dy=52, Dz=26
To know more about determinants from the given link.
https://brainly.com/question/24254106
#SPJ1
Write the following rational expression in lowest term
Answers
Given rational expression is
\(\frac{t^2-4}{6t-12}\)Factor the numerator and denominator first.
\(\begin{gathered} t^2-4=t^2-2^2 \\ =(t+2)(t-2) \end{gathered}\)Factor the denominator 6t-12:
\(\begin{gathered} 6t-12=6t-6\cdot2 \\ =6(t-2) \end{gathered}\)So,
\(\begin{gathered} \frac{t^2-4}{6t-12}=\frac{(t+2)(t-2)}{6(t-2)} \\ =\frac{t+2}{6} \end{gathered}\)Therefore, the given expression in lowest form is
\(\frac{t+2}{6}\)Keep getting stuck on this question don’t really understand what to do

Answers
The Solution:
Given the functions below:
\(\begin{gathered} f(x)=-4x-8 \\ \text{and} \\ g(x)=3x^2+x \end{gathered}\)We are required to find the value of f(-1)g(2)
So,
\(f(-1)\text{ means that we should substitute -1 for x in f(x)}\)\(f(-1)=-4(-1)-8=4-8=-4\)Similarly,
g(2) means we should substitute 2 for x in g(x).
\(g(2)=3(2)^2+2=3(4)+2=12+2=14\)Now, we shall multiply f(-1) and g(2) together.
\(f(-1)g(2)=f(-1)\times g(2)=-4\times14=-56\)Therefore, the correct answer is [option C]
SOMEBODY HELP MATH 100 POINTS BRAINLIEST⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️ HELP MATH 100 POINTS BRAINLIEST ⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️HELP MATH 100 POINTS BRAINLIESTHELP MATH 100 POINTS BRAINLIEST⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️ HELP MATH 100 POINTS BRAINLIEST ⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️HELP MATH 100 POINTS BRAINLIESTHELP MATH 100 POINTS BRAINLIEST⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️ HELP MATH 100 POINTS BRAINLIEST ⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️HELP MATH 100 POINTS BRAINLIEST
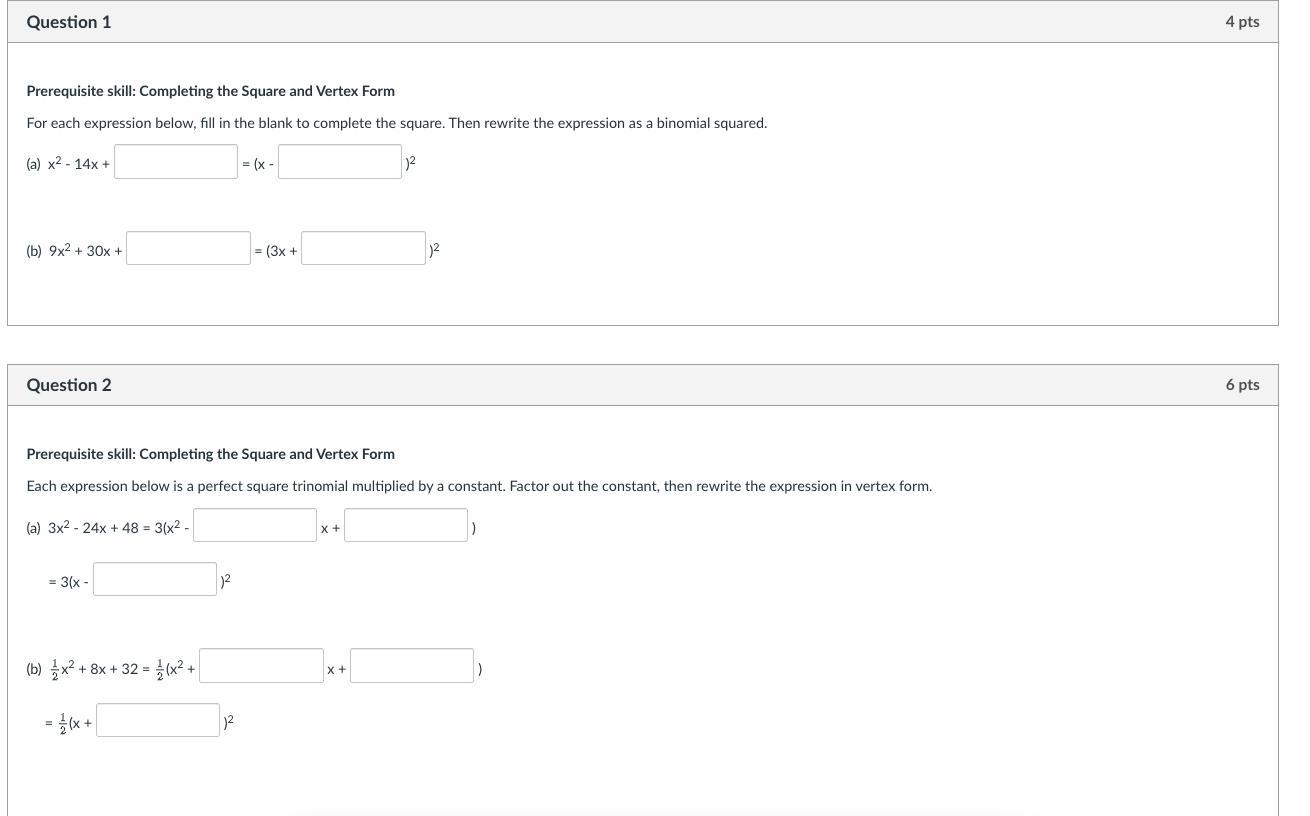
Answers
Answer:
\(\textsf{1.(a)} \quad x^2-14x+\boxed{49}=\left(x-\boxed{7}\right)^2\)
\(\textsf{1.(b)} \quad 9x^2 + 30x +\boxed{25}= \left(3x +\boxed{5}\right)^2\)
\(\begin{aligned}\textsf{2.(a)}\quad3x^2-24x+48&=3\left(x^2-\boxed{8}\:x+\boxed{16}\right)\\&=3\left(x-\boxed{4}\right)^2\end{aligned}\)
\(\begin{aligned}\textsf{2.(b)}\quad \dfrac{1}{2}x^2+8x+32&=\dfrac{1}{2}\left(x^2+\boxed{16}\:x+\boxed{64}\right)\\&=\dfrac{1}{2}\left(x+\boxed{8}\right)^2\end{aligned}\)
Step-by-step explanation:
Question 1(a) When completing the square for a quadratic equation in the form ax² + bx + c where the leading coefficient is one, we need to add the square of half the coefficient of the x-term:
\(x^2-14x+\left(\dfrac{-14}{2}\right)^2\)
\(x^2-14x+\left(-7\right)^2\)
\(x^2-14x+49\)
We have now created a perfect square trinomial in the form a² - 2ab + b². To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2 -2ab + b^2 = (a -b)^2}\)
Therefore:
\(a^2=x^2 \implies a=1\)
\(b^2=49=7^2\implies b = 7\)
Therefore, the perfect square trinomial rewritten as a binomial squared is:
\(x^2-14x+\boxed{49}=\left(x-\boxed{7}\right)^2\)
(b) When completing the square for a quadratic equation where the leading coefficient is not one, we need to add the square of the coefficient of the x-term once it is halved and divided by the leading coefficient, and then multiply it by the leading coefficient:
\(9x^2 + 30x +9\left(\dfrac{30}{2 \cdot 9}\right)^2\)
\(9x^2 + 30x +9\left(\dfrac{5}{3}\right)^2\)
\(9x^2 + 30x +9 \cdot \dfrac{25}{9}\)
\(9x^2 + 30x +25\)
We have now created a perfect square trinomial in the form a² + 2ab + b². To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2 +2ab + b^2 = (a +b)^2}\)
Therefore:
\(a^2=9x^2 = (3x)^2 \implies a = 3x\)
\(b^2=25 = 5^2 \implies b = 5\)
Therefore, the perfect square trinomial rewritten as a binomial squared is:
\(9x^2 + 30x +\boxed{25}= \left(3x +\boxed{5}\right)^2\)
\(\hrulefill\)
Question 2(a) Factor out the leading coefficient 3 from the given expression:
\(3x^2-24x+48=3\left(x^2-\boxed{8}\:x+\boxed{16}\right)\)
We have now created a perfect square trinomial in the form a² - 2ab + b² inside the parentheses. To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2 -2ab + b^2 = (a -b)^2}\)
Factor the perfect square trinomial inside the parentheses:
\(=3\left(x-\boxed{4}\right)^2\)
(a) Factor out the leading coefficient 1/2 from the given expression:
\(\dfrac{1}{2}x^2+8x+32=\dfrac{1}{2}\left(x^2+\boxed{16}\:x+\boxed{64}\right)\)
We have now created a perfect square trinomial in the form a² + 2ab + b² inside the parentheses. To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2+2ab + b^2 = (a +b)^2}\)
Factor the perfect square trinomial inside the parentheses:
\(=\dfrac{1}{2}\left(x+\boxed{8}\right)^2\)
Step-by-step explanation:
Since ABCD is a rectangle
⇒ AB = CD and BC = AD
x + y = 30 …………….. (i)
x – y = 14 ……………. (ii)
(i) + (ii) ⇒ 2x = 44
⇒ x = 22
Plug in x = 22 in (i)
⇒ 22 + y = 30
⇒ y = 8
Need help on this please

Answers
\(9 (4\sqrt{5x {}^{} } ) - 2(4 \sqrt{5x}) = 5(4 \sqrt{5x} )\)
Hope this helped ya!
Find the value of x. Then, find the measure of each labelled angle.
x=_
(7x+10)°=_
(15x+16)°=_

Answers
Answer:
x = 7deg
Step-by-step explanation:
7x + 10 + 15x + 16 = 180 (angles adjacent to each other in a //polygon are supplementary)
22x = 154
x = 7deg
This is a question on polygons and angles. If you wish to venture further into it/understand this topic better, you may want to follow my Instagram account (learntionary), where I post some of my own notes on certain topics and also some tips that may be useful to you :)
Write an equation that represents the line.
Use exact numbers.

Answers
Answer:
y=5/6x+8/3
Step-by-step explanation:
Let's use the slope-intercept form:
y=mx+b
m: slope
b: y-intercept
x and y: x and y coordinate pair
We start by finding the slope.
Slope = (y₂-y₁)/(x₂-x₁)
Slope = (6-1)/(4-(-2)) These are the two points on the line given to us
Slope = 5/6
Now we find the y-intercept:
y=5/6x+b
We can plug in one of the x and y coordinate pairs into the equation:
6=5/6(4)+b
6=10/3+b
b=8/3
Since we have the y-intercept and the slope, we can write the equation:
y=5/6x+8/3
Answer:
Step-by-step explanation:
( - 2 , 1 )
( 4 , 6 )
m = \(\frac{1-6}{-2-4}\) = \(\frac{5}{6}\)
y - 6 = \(\frac{5}{6}\) ( x - 4 )
y = \(\frac{5}{6}\) x - \(\frac{10}{3}\) + 6
y = \(\frac{5}{6}\) x + \(\frac{8}{3}\)

A simple random sample of 60 households in city 1 is taken. In the sample, there are 45 households that decorate their houses with lights for the holidays. A simple random sample of 50 households is also taken from the neighboring city 2. In the sample, there are 40 households that decorate their houses. What is a 95% confidence interval for the difference in population proportions of households that decorate their houses with lights for the holidays
Answers
Answer:
The calculated value of z = - 0.197 falls in the critical region therefore we reject the null hypothesis and conclude that at the 5% significance level there is significant difference in population proportions of households that decorate their houses with lights for the holidays
Step-by-step explanation:
We formulate the null and alternative hypotheses as
H0: p1= p2 there is no difference in population proportions of households that decorate their houses with lights for the holidays
against Ha : p1≠ p2 (claim) ( two sided)
The significance level is set at ∝= 0.05
The critical value for two tailed test at alpha=0.05 is ± 1.96
or Z∝= 0.05/2= ± 1.96
The test statistic is
Z = p1-p2/√pq(1/n1 +1/n2)
p1= proportions of households decorating in city 1 = 45/60=0.75
p2= proportions of households decorating in city 2 = 40/50= 0.8
p = the common proportion on the assumption that the two proportion are same.
p = \(\frac{n_1p_1 +n_2p_2}{n_1+n_2}\)
Calculating
p =60 (0.75) + 50 (0.8) / 110
p= 45+ 40/110= 85/110 = 0.772
so q = 1-p= 1- 0.772= 0.227
Putting the values in the test statistic and calculating
z= 0.75- 0.8/ √0.772*0.227( 1/60 + 1/50)
z= -0.05/√ 0.175244 ( 110/300)
z= -0.05/0.25348
z= -0.197
The calculated value of z = - 0.197 falls in the critical region therefore we reject the null hypothesis and conclude that at the 5% significance level there is significant difference in population proportions of households that decorate their houses with lights for the holidays
What are t + 8 + 3t terms and like
Answers
Answer:
t+8+3t
8+4t
Step-by-step explanation:
I guess the question is incomplete
A student bikes 5000 m East to school in 30.0 min (1800 seconds), realizes he forgot his calculator for physics, spends 30.0 min (1800 seconds) going back going home, and then races back to school in 27.0 minutes (1620 seconds).
What is the student’s total distance traveled?
_______ meters
The number of seconds it took the student to travel back and forth is ________
seconds.
Determine the student’s average speed. ________
m/s
Answers
The total distance covered is 15000 m. The total time taken is 5220 seconds and the speed is 2.87 m/s.
What is the speed?We know that speed has to do with the ratio of the distance that has been covered to the time taken. The speed is a scalar quantity and as such we do not consider the direction hence we would not consider that going back in the opposite direction. The total distance can be obtained algebraically.
The total distance that the student travelled can be obtained from;
5000 m + 5000 m + 5000 m
= 15000 m
The total time taken in seconds = 1800 seconds + 1800 seconds + 1620 seconds
= 5220 second
Speed = Distance/ Time
= 15000 m/5220 second
= 2.87 m/s
Learn more about speed:https://brainly.com/question/28224010
#SPJ1
Brainlist will be marked if right

Answers
Answer:
B is the linear relationship
Answer:
second option where y = 8, 16 and 24
Step-by-step explanation:
second option where y = 8, 16 and 24
This table shows a linear relationship because the y-values increase by the same amount each time (i.e. the difference between the y-values is the same).
If x=5 and y=7, evaluate the following expression:
20−(3y−4x)
Answers
Answer:
\(\huge\boxed{\bf\:19}\)
Step-by-step explanation:
Given,
x = 5y = 7Now, the expression is: \(20 - (3y - 4x)\).
To solve this question we just need to substitute the values of x & y in the given expression. Then,
\(20 - (3y - 4x)\\= 20 - (3(7) - 4(5))\\= 20 - (21 - 20)\\= 20 - 1\\= \boxed{\bf\:19}\)
\(\rule{150pt}{2pt}\)
8/10-5/10 help me i need to do this for math
Answers
Answer:
3/10
Step-by-step explanation:
Answer:
\(\frac{3}{10}\)
Step-by-step explanation:
\(\frac{8}{10}\) - \(\frac{5}{10}\) = \(\frac{3}{10}\)
Hope this helps. Plz give brainliest.
Find the length of the missing leg in the following triangle

Answers
Answer:
9
Step-by-step explanation:
a² +b²=c²
a²+40²=41²
a²=41²-40²
a²= 81
\( \sqrt{ {a}^{2} } = \sqrt{81} \)
a=9
749/d * d/749 = 1
d=?
Answers
Answer:
D=1
Step-by-step explanation:
1. Combine multiplied terms into a single fraction
2. Cancel terms that are in both numerator and denominator
3. Divide by 1
Answer:
I honestly don't know but I think its all real numbers but not zero
Step-by-step explanation:
If we have the following equations, y = 2x + 6 and 3y = 3x - 5, which function
has the highest rate of change?
Answers
In the xy-coordinate plane, the points (4, 2) and (-1, k) are on a line that is perpendicular to the line y=2x+1 . What is the value of k
Answers
A line of two points (4, 2) and (-1, k) is perpendicular to the line y=2x+1, then k = 9/2.
Given a line with equation y = mx + c, the slope is denoted by m.
Given 2 points with slopes m₁ and m₂, those two lines are perpendicular if:
m₁ x m₂ = -1
The given line equation is: y = 2x+1
Hence,
m₁ = 2
Compute the slope from 2 points: (4, 2) and (-1, k)
m₂ = (k - 2) / (-1 - 4)
m₂ = (-1/5) (k - 2)
Use the condition for perpendicular lines:
m₁ x m₂ = -1
2 x (-1/5) (k - 2) = -1
2k - 4 = 5
2k = 9
k = 9/2
Learn more about line equation here:
https://brainly.com/question/29813143
#SPJ4
The height (in centimeters) of a candle is a linear function of the amount of time (in hours) it has been burning. When graphed, the function gives a line with a slope of −0.4. See the figure below. Suppose that the height of the candle after 11 hours is 16.6 centimeters. What was the height of the candle after 6 hours?

Answers
Answer:
height of the candle after 6 hours= 18.6 centimeters
Step-by-step explanation:
the function gives a line with a slope of −0.4.
the height of the candle after 11 hours is 16.6 centimeters.
after 6 hours, the height will be
But slope= y2-y1/x2-x1
Y2 is the unknown
Y1 = 16.6
X1= 11 hours
X2= 6 hours
y2-y1/x2-x1= -0.4
(Y2-16.6)/(6-11)= -0.4
(Y2-16.6)/(-5)= -0.4
(Y2-16.6)= -5( -0.4)
(Y2-16.6)= 2
Y2 = 2+16.6
Y2 = 18.6 centimeters
height of the candle after 6 hours= 18.6 centimeters
Help I need done quick

Answers
Answer: 160
Step-by-step explanation:
I divided 144/9 to see how many students are their per 10% of the 90% of students and got the answer 16. I then added 16 as the other missing 10% to 144 and got the answer 160.
Sarah wants to install carpet to cover her rectangular dining room floor, which has a length of 12 feet and a width of 9 feet. The cost to install the carpet is $5 per square foot. Sarah predicts that the total cost to install the carpet will be $500. Which statement BEST explains why Sarah’s prediction is incorrect? PLS HELP TY
A. Sarah rounded the area of the floor to 110 square feet.
B. Sarah rounded the area of the floor to 100 square feet.
C. Sarah rounded the area of the floor to 98 square feet.
D. Sarah rounded the area of the floor to 108 square feet.
Answers
Answer:
B
Step-by-step explanation:
12 long 9 wide = 12*9 =108 sqft
$5/sqft
so she'll need 108*5 =540
but she rounded to 100 sqft
The shape of a telescope lens approximated by the equation y = 0.0023x ^ 2 + 2.758 * 10 ^ - 16 Describe the relationship
Answers
It is non-linear but it is proportional
Therefore, the correct option is:
A. Non-linear and proportional