There are 5 machines each of which when running suffers breakdown at an average rate of 2 per hour. There are 2 servicemen and only one man work on a machine at a time. If ‘n’ machine are out of order when n > 2 then (n – 2) of them wait until a service man is free. Once a serviceman starts work on a machine the time to complete the repair has an exponential distribution with mean of 5 minutes. Find the distribution of the number of machines out of action at a given time. Find also the average time an out-of-action machine has to spend waiting for the repairs to start
Answers
- The distribution of the number of machines out of action at a given time is Poisson(2). - The average time an out-of-action machine has to spend follows an Exponential distribution with a mean of 5 minutes.
Given that each machine suffers breakdown at an average rate of 2 per hour, we can model the breakdown process as a Poisson distribution with a rate parameter λ = 2.
The number of machines out of action at a given time follows a Poisson distribution. Let's denote this random variable as X.
X ~ Poisson(λ), where λ is the rate parameter.
For the given scenario, λ is the average number of breakdowns per hour, which is 2.
To find the average time an out-of-action machine has to spend waiting for the repairs to start, we need to consider the following:
When n > 2 machines are out of order, (n - 2) machines have to wait until a serviceman is free.
Once a serviceman starts work on a machine, the time to complete the repair follows an exponential distribution with a mean of 5 minutes.
Let's denote the random variable Y as the time spent waiting for repairs to start on an out-of-action machine:
Y ~ Exponential(1/5), where 1/5 is the rate parameter (μ) representing the mean repair time of 5 minutes.
Learn more about Exponential distribution here:
https://brainly.com/question/30481829
#SPJ11
Related Questions
An aunt decides to give $2000 to her niece and nephew. She divided it into the ratio of their ages. If
the girl is 13 years old and the boy is 12 years old, how much will each get?
Answers
Step-by-step explanation:
The Niece is 13 years old
The nephew is 12 years old
the summation of their ages is 25
if $2000 was shared among them
The Niece:
13/25 x 2000/1
0.54 x 2000 = $1040
Nephew:
12/25 x 2000/1
0.48 x 2000
= $960
what is the greatest possible product of a four digit number and a three digit number obtained from seven distinct digits
Answers
the greatest possible product of a four-digit number and a three-digit number obtained from seven distinct digits is 2,463,534.
To find the greatest possible product of a four-digit number and a three-digit number obtained from seven distinct digits, we can start by considering the largest possible values for each digit.
Since we need to use seven distinct digits, let's assume we have the digits 1, 2, 3, 4, 5, 6, and 7 available.
To maximize the product, we want to use the largest digits in the higher place values and the smallest digits in the lower place values.
For the four-digit number, we can arrange the digits in descending order: 7, 6, 5, 4.
For the three-digit number, we can arrange the digits in descending order: 3, 2, 1.
Now, we multiply these two numbers to find the greatest possible product:
7,654 * 321 = 2,463,534
To know more about number visit:
brainly.com/question/3589540
#SPJ11
which equation is true for the value b=2a. 2b+24=30b. 3b-2=4c. b+4=8d. 2b-3=0
Answers
3(2)-2=4, the second is true. the answerb is b
3x + 6 =
plss help me with this
Answers
Answer:
3× + 6
3+6=9
9×3=3
Finish
Answer:
3
(
+
2
)Step-by-step explanation:
4) What is the value of v?

Answers
Answer:
v = 110
Step-by-step explanation:
The big line is a 180 degree line. We need to find the value of the missing side so we take 70 degrees and subtract it from the total angle 180 degrees. That leaves us 110 degrees, so v = 110 degrees.
Raymond's hair was 13 centimeters long after his last haircut, and it grows 7 centimeters
every year. Raymond last got his hair cut 6 years ago. How long is it now? Write and solve an
equation to find the answer.
Answers
Equation - 13 + 7(6) = x
Solved Answer - 55
Explanation:
Not the best at writing equations, but I’ll try
13 + 7(6) = x
13 + 42 = x
55 = x
A ball dropped vertically falls d metres in t seconds
d is directly proportional to the square of t
Answers
The constant of proportionality, k, is 5.
In the next 8 seconds, the ball will drop 320 metres.
Given that the distance fallen, denoted as d, is directly proportional to the square of time, denoted as t, we can express this relationship as:
d ∝ t²
To find the constant of proportionality, we can use the information provided. It states that the ball drops 80 metres in the first 4 seconds. Substituting these values into the proportionality equation, we have:
80 ∝ 4²
Simplifying, we have:
80 ∝ 16
To determine the constant of proportionality, we divide both sides of the equation by 16:
80/16 = 5 = k
Therefore, the constant of proportionality, k, is 5.
Now that we have determined the constant of proportionality, we can use it to find the distance the ball drops in the next 8 seconds. We substitute the value of t = 8 into the proportionality equation:
d = k * t²
d = 5 * 8²
d = 5 * 64
d = 320
Therefore, in the next 8 seconds, the ball will drop 320 metres.
for such more question on distance
https://brainly.com/question/12356021
#SPJ8
Question
A ball, dropped vertically, falls d metres in t seconds. D is directly proportional to the square of t. The ball drops 80 metres in the first 4 seconds. How far does the ball drop in the next 8 seconds?
Aisha is picking out some movies to rent, and she is primarily interested in children's movies and comedies. She has narrowed down her selections to 15 children's movies and 11 comedies. How many different combinations of 33 movies can she rent if she wants at least one comedy?
Answers
To determine the different combinations of 33 movies that Aisha can rent if she wants at least one comedy, we can use the combination formula as follows: nCr = n! / r! (n - r)!
Where n is the total number of movies available, r is the number of movies Aisha wants to rent, and nCr represents the number of combinations.
To find the number of combinations when Aisha wants to rent at least one comedy, we can use the complement rule which states that the probability of an event occurring is equal to 1 minus the probability of the event not occurring. In this case, the probability of Aisha not renting any comedy is equal to the number of combinations of 33 movies she can rent without a comedy divided by the total number of combinations possible. We can then subtract this probability from 1 to find the probability of Aisha renting at least one comedy.
Number of combinations of 33 movies without a comedy = nCr = 15C33 = 0 (since there are only 15 children's movies available and Aisha wants to rent 33 movies)
Total number of combinations possible = nCr = (15 + 11)C33 = 26C33
Using the complement rule,
Probability of Aisha not renting any comedy = 0 / 26C33 = 0
Probability of Aisha renting at least one comedy = 1 - 0 = 1
Therefore, Aisha can rent all the 33 movies since the probability of her not renting any comedy is zero. The number of different combinations of 33 movies she can rent is therefore equal to the total number of combinations possible, which is 26C33.
Know more about complement rule here:
https://brainly.com/question/29146128
#SPJ11
I need help
Solving this problem

Answers
The required value of x is 22 degrees for the given figure.
Adjacent angles are a sort of additional angle. Adjacent angles share a common side and vertex, such as a corner point. Their points do not overlap in any manner.
As we know that supplementary angles are defined as when pairing of angles addition to 180° then they are called supplementary angles.:
According to the given figure, it can be written as follows:
2x + 24 + 6x - 20 = 180
8x + 4 = 180
8x = 180 - 4
8x = 176
x = 176/8
x = 22
Therefore, the required value of x is 22 degrees for the given figure.
Learn more about supplementary angles here:
brainly.com/question/3027144
#SPJ1
The complete question is as follows:
Find the value of x for the below figure.

Last year Tyler used 60 feet of fencing to enclose a rectangular garden with an area of 200 ft². This year Tyler plans to use 120 feet of fencing to enclose a garden similar in shape. What will be the area of the garden?
Answers
Answer:
Area of new garden = 800 ft²
Step-by-step explanation:
Given:
Old fencing = Parameter of old garden = 60 ft
Area of old garden = 200 ft
Find:
Area of new garden if Parameter of new garden is 120 ft
Computation:
Assume;
Length of old garden = l
Width of old garden = b
So,
2[l + b] = 60
l + b = 30
l = 30 - b
Area of old garden = 200 ft
l x b = 200
So,
(30 - b)b = 200
b² - 30b + 200 = 0
b² - 20b - 10b + 200
b(b-20) - 10(b-20)
(b-20)(b-10)
So,
Width of old garden = 10 ft
Length of old garden = 20 ft
New parameter is double
So,
Width of new garden = 10 x 2 = 20 feet
Length of old garden = 20 x 2 = 40 feet
Area of new garden = l x b
Area of new garden = 20 x 40
Area of new garden = 800 ft²
I will mark as brainly please hurry!
Nicholas started a canned-food drive at school. The equation representing this is y = 235x + 15, where x is the number of days, and y is the number of cans collected. Explain how to determine how many days it would take to collect 2600 cans.
Answers
Answer:
just divide and add x and y
Step-by-step explanation:
Answer:
11 days
Step-by-step explanation:
2600 = 235x+15
- 1 5 - 15
2585 235x
/235 /235
11 = x
For the standard normal random variable z, find z for each situation. If required, round your answers to two decimal places. For those boxes in which you must enter subtractive or negative numbers use a minus sign. (Example: -300)'
a. The area to the left of z is 0.1827. z =
b. The area between −z and z is 0.9830. z =
c. The area between −z and z is 0.2148. z =
d. The area to the left of z is 0.9997. z =
e. The area to the right of z is 0.6847. z=
Answers
The z-values for the given situations are approximate:
a. The area to the left of z is 0.1827. z = -0.90
b. The area between −z and z is 0.9830. z = 2.17
c. The area between −z and z is 0.2148. z = 0.85
d. The area to the left of z is 0.9997. z = 3.49
e. The area to the right of z is 0.6847. z= -0.48
a. For an area of 0.1827 to the left of z, the corresponding z-value can be found using a standard normal distribution table or a statistical calculator. The z-value is approximately -0.90.
b. To find the z-value for an area between -z and z equal to 0.9830, we need to find the value that corresponds to (1 - 0.9830)/2 = 0.0085 in the upper tail of the standard normal distribution. Using the table or calculator, the z-value is approximately 2.17.
c. Similarly, for an area between -z and z equal to 0.2148, we find the value that corresponds to (1 - 0.2148)/2 = 0.3926 in the upper tail. The z-value is approximately 0.85.
d. For an area of 0.9997 to the left of z, we find the value that corresponds to 0.9997 in the upper tail. The z-value is approximately 3.49.
e. To find the z-value for an area to the right of z equal to 0.6847, we find the value that corresponds to 1 - 0.6847 = 0.3153 in the upper tail. The z-value is approximately -0.48.
In summary, the z-values for the given situations are approximate:
a. -0.90
b. 2.17
c. 0.85
d. 3.49
e. -0.48
These values can be used to determine the corresponding percentiles or probabilities for the standard normal distribution. The values are typically found using standard normal distribution tables or statistical calculators that provide the cumulative probability distribution function (CDF) for the standard normal distribution.
For more such answers on z-values
https://brainly.com/question/28000192
#SPJ8
The supplement of an angle is 129 what is the measure of the angle
Answers
Answer:
51
Step-by-step explanation:
A cake decorator mixed 3 cups of red frosting with 7 cups of blue frosting to make a purple frosting. Which ratio of cups of red frosting to cups of blue frosting will make the same shade of purple frosting?
Answers
Answer: 3 to 10. will be the ratio.
Step-by-step explanation:
A company uses samples of size 9 to construct an X-bar chart to control the mean of the diameter of a drive shaft. On a certain day, a new employee takes a sample of size 4 and plot this sample average on the X-bar chart that is constructed with samples of size 9. Assuming the process is in control, what is the probability that this sample average falls outside the 3- sigma control limits of the X-bar chart?
Group of answer choices
0.00%
0.27%
1.24%
4.55%
13.36%
18.35%
31.73%
Answers
The probability that the sample average falls outside the 3-sigma control limits of the X-bar chart is 0.27%.
The 3-sigma control limits are calculated using the standard deviation of the process. If the process is in control, then 99.73% of the sample averages will fall within the 3-sigma control limits. The remaining 0.27% of the sample averages will fall outside the control limits.
In this case, the sample size is 4, which is smaller than the sample size of 9 that was used to construct the control chart. This means that the control limits for the sample of size 4 will be narrower than the control limits for the sample of size 9.
As a result, the probability that the sample average falls outside the control limits will be higher for the sample of size 4.
Specifically, the probability that the sample average falls outside the 3-sigma control limits for a sample of size 4 is 0.27%. This means that there is a 0.27% chance that the new employee will observe a sample average that falls outside the control limits, even if the process is in control.
Visit here to learn more about probability:
brainly.com/question/13604758
#SPJ11
A granola recipe calls for 2 1/3 (mixed number 2 and 1/3) cups of almonds. A bag of almonds contains 2 cups. To make 2 1/2 (mixed number 2 and 1/2) batches of granola, Ali buys 5 bags of almonds. How many cups of almonds will he have left over?
Answers
Answer:
4 1/6 cups of almonds left
Step-by-step explanation:
Granola recipe = 2 1/3 cups of almonds
2 1/2 batches of granola = 2 1/3 cups of almonds × 2 1/2
= 2 1/3 × 2 1/2
= 7/3 × 5/2
= (7*5)/(3*2)
= 35/6
= 5 5/6 cups of almonds
A bag of almonds = 2 cups
5 bags of almonds = 10 cups
Cups of almonds left = 10 cups - 35/6 cups
= 60-35/6
= 25/6
= 4 1/6 cups
Travis makes 3.80 l of dessert. he wants to fill 250 ml cups with the dessert. which calculation can be used to determine the number of cups travis can fill?
Answers
Convert 3.80 liters to milliliters, multiply by 1000, divide by 250, find 15.2 cups Travis can fill with 3.80 liters.
To determine the number of cups Travis can fill with 3.80 liters of dessert, we need to convert the volume from liters to milliliters. Since there are 1000 milliliters in 1 liter, we can calculate the total volume of the dessert in milliliters by multiplying 3.80 liters by 1000:
3.80 liters * 1000 ml/liter = 3800 ml
Next, we divide the total volume of the dessert (3800 ml) by the volume of each cup (250 ml) to find the number of cups Travis can fill:
3800 ml / 250 ml/cup = 15.2 cups
Therefore, Travis can fill approximately 15.2 cups with the 3.80 liters of dessert.
To know more about volume Visit:
https://brainly.com/question/28058531
#SPJ11
BRAINLY TO WHOEVER CAN HELP PLS OMG ASAP

Answers
Answer:
1: C
2:A
Step-by-step explanation:
Dialation is just the multiplucation of the size. If the original point is 2, 4 dialated to 2 is would be 4, 8. Basiccly just multiply by 2 in this example.
What is the slope of the line shown?

Answers
Answer:
The slope is 3
Step-by-step explanation:
\( \frac{6 - 0}{0 - ( - 2)} = \frac{6 - 0}{0 + 2} = \frac{6}{2} = 3\)
Hope it is helpful dear ✌️✌️✌️✌️
suppose you have an argument that has three premises, all of which are true, and a true conclusion. if so, then the argument must be
Answers
The conclusion might be accurate or inaccurate.
The conclusion could be true or false if an argument has some true premises and some false premises and is valid. You only know that the premises cannot both be true and the conclusion must be false because the argument is sound. But the incorrect premises already rule out the possibility of possessing this set of truth values (that is, you cannot have all true premises). As a result, the argument's validity is unaffected whether the conclusion is true or untrue. As a result, the conclusion of an argument that contains only false premises may or may not be true.
Can an argument have all true premises and a false conclusion?TRUE. A valid argument cannot, by definition, have a false conclusion and all true premises.
Therefore, a valid argument must have an erroneous premise if it has a false conclusion.
To learn more about true premises and a false conclusion visit:
https://brainly.com/question/15019295
#SPJ4
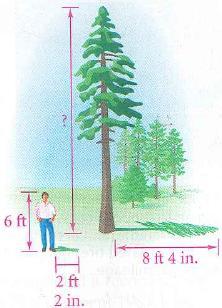
Suppose you work on a tree farm and you need to find the height of each tree. You know that the length of an object with its height. Find the constant of variation
Answers
Answer:
The answer is below
Step-by-step explanation:
Suppose you work on a tree farm and you need to find the height of each tree. You know that the length of an object varies directly with its height. a) Find the constant of variation b) find the height of the tree
Solution:
a) Let y represent the length of an object and x represent the height of the object. Given that y ∝ x. Let k be the constant of variation, therefore the relationship between y and x is:
y = kx
y = 2 ft 2 in = 13/6 ft (1 ft = 12 in)
x = 6 ft
Substituting gives:
13/6 = k(6)
k = 13/6 ÷ 6
k = 13/36
b) y = (13/36)x
Given that y = 8ft 4 in = 25/3 ft
Substituting:
y = (13/36)x
25/3 = (13/36)x
x = 25/3 ÷ (13/36)
x= 300/13 ft ≈ 23 ft
Simplify the expression completely.
-3V24 - V.
Answers
Answer:
-V (3 V^23 + 1)
Step-by-step explanation:
Simplify the following:
-3 V^24 - V
Factor -V out of -3 V^24 - V:
Answer: -V (3 V^23 + 1)
A triangle has a 40 degree angle and a 35 degree angle. What is the measure of the third angle? 75 degrees 75 degrees 95 degrees 95 degrees 105 degrees 105 degrees 125 degrees
Answers
Answer:
105°
Step-by-step explanation:
Bya angle sum property of triangle
40+35+x=180
x= 180-75
x= 105°
Hope it helps you
Write the equation of the line that passes through the points ( 9 , − 7 ) (9,−7) and ( − 5 , 3 ) (−5,3). Put your answer in fully simplified point-slope form, unless it is a vertical or horizontal line.

Answers
The equation of line is y = -5/7 x -4/7.
we have the points (9,−7) and ( − 5 , 3 ).
So, slope of line
= (3 + 7)/ (-5 -9)
= 10 / (-14)
= -5/7
and, the equation of line is
y + 7 = -5/7 (x - 9)
y+ 7 = -5/7 x + 45/7
y = -5/7 x + 45/7 - 7
y = -5/7 x -4/7
Learn more about Slope here:
https://brainly.com/question/3605446
#SPJ1
Which of the following is/are correct? (Select all that apply. You have only one submission for this question.) If u and v are parallel, then either u.v=jul lvl or u. V-lul lvl. The vector projuv is parallel to v If u and v are orthogonal, then u xv = 0. The expression u. (vw) is meaningful and the result is a scalar. Suppose u: O. If u xv=uxw, it follows that vw. If u and v are parallel, then u xv = 0. The expression u u can be negative
Answers
The correct statements are If u and v are orthogonal, then u × v = 0. The vector proj_v u is parallel to v. If u and v are parallel, then u × v = 0.
The statement "If u and v are parallel, then either u · v = |u||v|" is incorrect. The correct statement is "If u and v are parallel, then u · v = |u||v|".
The statement "The expression u.(vw) is meaningful and the result is a scalar" is incorrect. The expression u.(vw) is not meaningful because the dot product is only defined for vectors of the same dimension.
The statement "Suppose u: O. If u × v = u × w, it follows that v = w" is incorrect. The correct statement is "Suppose u ≠ 0. If u × v = u × w, it follows that v - w is parallel to u".
Finally, the statement "The expression u · u can be negative" is incorrect. The dot product u · u is always non-negative, and is only equal to zero if and only if u = 0
Learn more about orthogonal here
https://brainly.com/question/31043750
#SPJ11.
use graphing the solve the systems of equations? x^2+6x+8 and x+4
Answers
The solution of the given system of equations is (-2, -4).
The given system of equations is:x² + 6x + 8 = 0x + 4 = 0To solve the system using graphing, follow the given steps below:Step 1: Graph both the equations on the same coordinate axes. For this, rewrite the given quadratic equation as y = x² + 6x + 8. Then, draw the graphs of y = x² + 6x + 8 and y = -4 on the same coordinate plane. The graphs of both equations intersect at x = -2. Therefore, the solution of the system is (-2, -4).
The graph of y = x² + 6x + 8 is given below: The graph of y = -4 is a straight horizontal line passing through the point (-4, 0).The graph of both the equations on the same coordinate axes is given below: Step 2: Identify the point of intersection of the graphs. The point of intersection of the graphs is the solution of the system. Therefore, the solution of the system is (-2, -4).
For more such questions on equations
https://brainly.com/question/29174899
#SPJ8
Which of the following is a Linear Inequality in Two Variables?
A. 2x² + 3y ≥ 6
B. 3x + 6y ≤ 9
C. 7x + 2y = 8
D. 2x - 7 < 12
Answers
The linear inequality in two variables is 3x + 6y ≤ 9 . Option B
What is linear inequality?Linear inequalities are inequalities that involve at least one linear algebraic expression, that is, a polynomial of degree 1 is compared with another
Inequalities are math expressions or statements that use the inequalities "less than or equal to", "greater than or equal to", "less than", "greater than", and "not equal to".
Linear expressions are math statements or expressions whose expressions of a degree 1 (Highest exponent).
Variables are mathematical symbol or term that represents the unknown values.
In the problem, the question asks for a linear inequality in two variables. As you can see, all of the choices are linear expressions. The only option that uses one of the inequality symbols and has two unknown variables is the third option. So, it's the option B.
To learn more about linear inequalities at: https://brainly.com/question/29614696
#SPJ1
can you please help me
Step by step as well for brainliest

Answers
Answer:
Step-by-step explanation:
42:7=ED:24
cross multiply 42 into 24.
Then divide by 7
you will get ED
Then use pythageorous theorem.
Ed square + 42 square=Ef square
Then do square root of Ef square
Please just give me the answer

Answers
Answer:
x = 4
Step-by-step explanation:
We use the formula:
a² + b² = c²
x² + 3² = 5²
x² + 9 = 25
x² = 16
\(\sqrt{x^2} =\sqrt{16}\)
x = 4
Define a function in Scheme that
returns True if a matrix (list of lists) is symmetric and returns
False otherwise.
Answers
Here's a Scheme function that checks whether a matrix is symmetric or not:
```scheme
(define (is-symmetric-matrix matrix)
(define (get-element matrix i j)
(if (null? matrix)
#f
(if (= i 0)
(if (null? (car matrix))
#f
(if (= j 0)
(car (car matrix))
(get-element (cdr matrix) i (- j 1))))
(get-element (cdr matrix) (- i 1) j))))
(define (is-matrix-symmetric-helper matrix i j)
(if (null? matrix)
#t
(if (equal? (get-element matrix i j)
(get-element matrix j i))
(is-matrix-symmetric-helper matrix i (+ j 1))
#f)))
(if (null? matrix)
#t
(is-matrix-symmetric-helper matrix 0 0)))
```
The function `is-symmetric-matrix` takes a matrix as an input, which is represented as a list of lists. It uses a helper function called `is-matrix-symmetric-helper` to compare each element of the matrix with its corresponding element in the transposed position. The `get-element` function is used to retrieve the element at position `(i, j)` in the matrix.
The `is-matrix-symmetric-helper` function recursively iterates over the matrix, comparing each element with its transposed element. If any pair of corresponding elements is found to be different, it immediately returns `#f` (False), indicating that the matrix is not symmetric. If it reaches the end of the matrix without finding any differences, it returns `#t` (True), indicating that the matrix is symmetric.
Finally, the main `is-symmetric-matrix` function first checks if the matrix is empty. If it is, it immediately returns `#t` since an empty matrix is considered symmetric. Otherwise, it calls the helper function with the initial indices `(0, 0)` and returns its result.
Learn more about Scheme function: https://brainly.com/question/33167627
#SPJ11