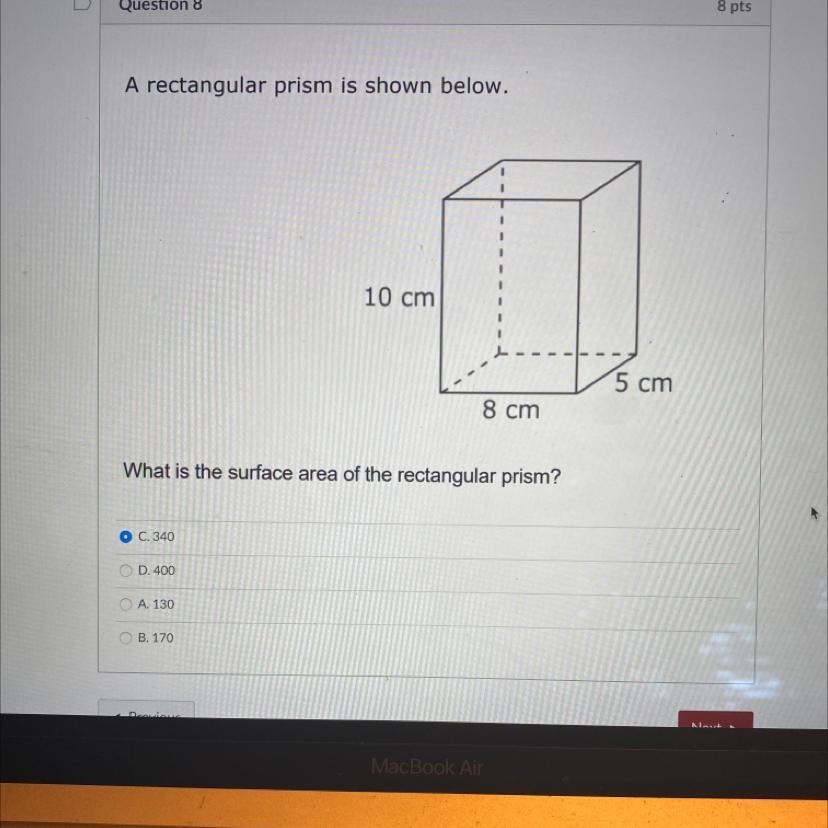
Answers
340 you were right
Step-by-step explanation:
Answer:
340
Step-by-step explanation:
first you have to find one side
i will go with 10 and 8
10*8=80
there are two of them
160 save this number in your bank
8*5=40 for the base
there are two of these too
80 save this number in your mental bank
for the last side 10 and 5
10*5=50 there are two of them
100
now add them all up
100+80+160=340
hope this helps!
Related Questions
Astorepays$87foracoat.Thestoremarksupthepriceby50%.Whatistheamountofthemark-up?
Answers
Answer:
87*0.5 = 43.5
43.5
Step-by-step explanation:
Please help on this answer
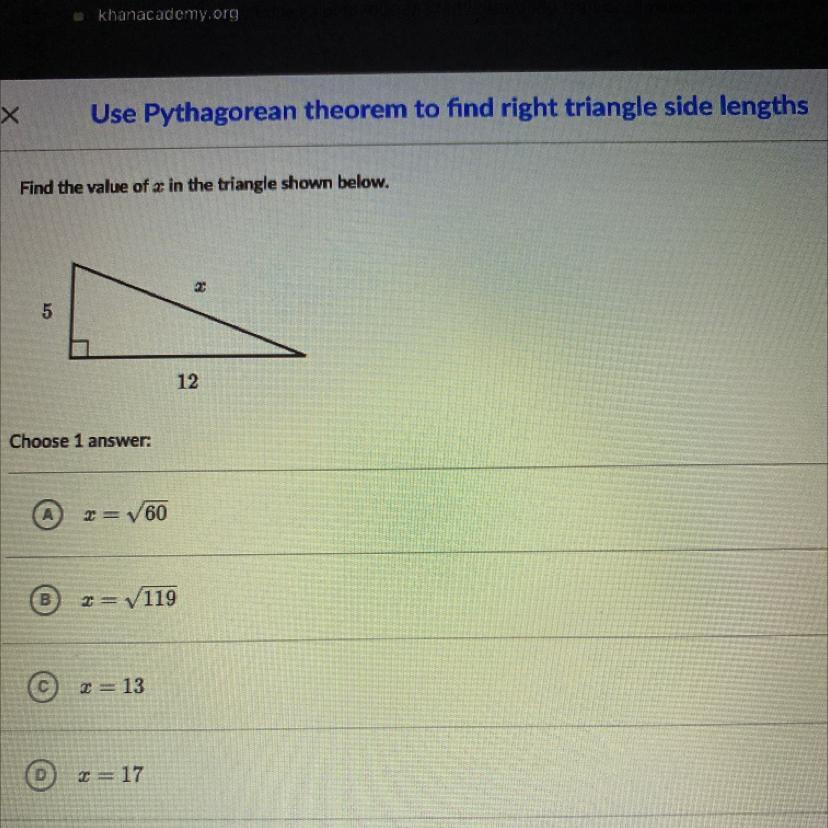
Answers
Answer:
Step-by-step explanation:
5^2 + 12^2 = x^2
25 + 144 = x^2
169 = x^2
13 = x
answer is C
Answer:
13
Step-by-step explanation:
Will mark brainliest.
What is pi?
Answers
Answer: 3.14159265358979.....
Step-by-step explanation:
Answer:
3.14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 59230 78164 06286 20899 86280 34825 34211 7067.
for the simple harmonic motion equation d=9 cos(pi/2t) what is the period
Answers
The period of the simple harmonic motion described by the equation d = 9 cos(pi/2t) is 4 seconds. The period is the time it takes for the motion to complete one full cycle, and in this case, it takes 4 seconds to do so.
To understand why the period is 4 seconds, let's examine the equation. The cosine function has a period of 2π radians or 360 degrees. In this equation, the argument of the cosine function is (π/2)t. To find the period, we need to determine the value of t that corresponds to one full cycle of the cosine function.
Since the argument is (π/2)t, one full cycle occurs when (π/2)t increases by 2π radians or 360 degrees. Solving for t, we have:
(π/2)t = 2π
Dividing both sides by π/2, we get:
t = 4
Therefore, the value of t that corresponds to one full cycle is 4 seconds, which is the period of the simple harmonic motion described by the equation.
Learn more about time period of SHM from here brainly.com/question/31082787
#SPJ11
what does d' measure
Answers
The difference between amount of two proportions is measured by D'.
D' is a metric for comparing differences between two proportions. It serves as a gauge for comparing how far apart the two proportions are from one another. It is determined by multiplying the difference between the two proportions by the sum of the standard deviations of the two proportions. The outcome is a measurement of how many standard deviations there are between the two proportions.
In statistical tests like the Chi-Square test or the Z-test, D' is most frequently employed to calculate the difference between two proportions. It is a helpful way to compare two proportions because it indicates whether or not the difference is statistically significant. Given that it takes into consideration the variability of each sample, it is especially helpful when comparing two proportions when the sample sizes are different. In data-mining applications, where it can be used to find correlations between two proportions, D' is also a helpful measure of the separation between two proportions.
Learn more about amount here
https://brainly.com/question/28970975
#SPJ4
A rotation of 180 degrees around the orgin will move a shape how many quadrants ?
Answers
Answer:
2 quadrants
Step-by-step explanation:
If it is 360 it would be 180 times 2 leading you back to where you started so 2 a point at (x,y) would turn into (-x,-y) when moved 180 degrees
solve this equation 3+√2/√5+√3
Answers
Answer:
5.36 is the answer thats what the calculator said.
Help i need the estimated difference between 3,475 and 7,652
Answers
Answer: 4177 rounds to 4180
Step-by-step explanation:
7652-3475=4177
4177 rounds to 4180
A sign painter must spend 8n^2/3+400 dollars to make n signs. how many signs can the painter make for $1200?
Answers
The sign painter can make 1000 signs for $1200. To solve this problem, we need to set up an equation that relates the cost of making n signs to the number of signs produced.
We are given that the cost is given by the expression \(8n^{2/3}\)+400. Therefore:
\(8n^{2/3}\) + 400 = cost
We want to find the number of signs that can be made for $1200. So we set up another equation:
\(8n^{2/3}\) + 400 = 1200
Simplifying this equation, we get:
\(8n^{2/3}\) = 800
\(n^{2/3}\) = 100
\(n^2\) = \(100^3\)
n = 1000
Therefore, the sign painter can make 1000 signs for $1200.
To check our answer, we can substitute n = 1000 into the original equation:
\(8n^{2/3}\) + 400 = \(8(1000)^{2/3}\) + 400 = 1200
So our answer is correct.
To learn more about number of signs, refer:-
https://brainly.com/question/29127048
#SPJ11
Please help and provide explanations!! Will mark as a brainliest !

Answers
The smallest possible value of x is 8.
Given:
LCM of x and 60 = 240
240 = 2*2*2*2*3*5
= \(2^{4} *3*5\)
60 = 2*2*5*3
= \(2^2*5*3\)
so x must have the same primes as 240.
x = \(2^i*3^j*5^k\)
i<=4 and j,k <= 1
so,
x = \(2^4\)
x = 8.
Therefore the smallest possible value of x is 8.
Learn more about the LCM here:
https://brainly.com/question/20739723
#SPJ1
the cost of 30 second commercial during the super bowl increased approximately linearly from 3.1 millions
Answers
If the cost of a 30-second commercial during the Super Bowl increased approximately linearly from 3.1 million, it means that there is a linear relationship between the cost and time.
To determine the exact relationship or equation, we would need more data points or information. However, based on the given information, we can describe the linear relationship between the cost (C) and time (T) using the slope-intercept form of a linear equation:
C = mT + b
Where:
C is the cost of the commercial
T is the time (in seconds)
m is the slope (rate of increase in cost per unit of time)
b is the y-intercept (initial cost at T = 0)
In this case, we know that the initial cost (when T = 0) is 3.1 million. Therefore, the equation becomes:
C = mT + 3.1 million
Without more data points or information, we cannot determine the exact value of the slope (m) or the equation of the linear relationship. To obtain a more accurate and specific equation, additional data or context is necessary.
Learn more about cost here:
https://brainly.com/question/14566816
#SPJ11
let r be the region bounded by the graphs of y=sin(pi x) and y=x^3-4x as shown in the figure above
Answers
Area shaded represents the area bounded by both the graphs of the functions y = sin(πx) and y = x³ - 4x.
What is the area bounded by two curves?An area bounded by two curves is the area under the smaller curve subtracted from the area under the larger curve. This will get you the difference, or the area between the two curves.
Given is the region {r} bounded by the graphs of y = sin(πx) and y = x³ - 4x.
Refer to the graph attached. The shaded region is the area bounded by both the graphs of the functions y = sin(πx) and y = x³ - 4x.
Therefore, area shaded represents the area bounded by both the graphs of the functions y = sin(πx) and y = x³ - 4x.
To solve more questions on graphs, visit the link below -
brainly.com/question/28951560
#SPJ1

A magazine advertises that a subscription price of $29.99 (for 12 issues) represents a savings of 70% from the newsstand price. What is th e price of one issue at the newsstand ?
Answers
I think the answer is 20.99
Matti is making moonshine in the woods behind his house. He’s
selling the moonshine in two different sized bottles: 0.5 litres
and 0.7 litres. The price he asks for a 0.5 litre bottle is 8€, for
a
Answers
Based on the calculation, it appears that Matti had approximately 94 bottles of 0.5 litres and 11 bottles of 0.7 litres in the last patch of moonshine that he sold.
To solve the problem using the determinant method (Cramer's rule), we need to set up a system of equations based on the given information and then solve for the unknowns, which represent the number of 0.5 litre bottles and 0.7 litre bottles.
Let's denote the number of 0.5 litre bottles as x and the number of 0.7 litre bottles as y.
From the given information, we can set up the following equations:
Equation 1: 0.5x + 0.7y = 16.5 (total volume of moonshine)
Equation 2: 8x + 10y = 246 (total earnings from selling moonshine)
We now have a system of linear equations. To solve it using Cramer's rule, we'll find the determinants of various matrices.
Let's calculate the determinants:
D = determinant of the coefficient matrix
Dx = determinant of the matrix obtained by replacing the x column with the constants
Dy = determinant of the matrix obtained by replacing the y column with the constants
Using Cramer's rule, we can find the values of x and y:
x = Dx / D
y = Dy / D
Now, let's calculate the determinants:
D = (0.5)(10) - (0.7)(8) = -1.6
Dx = (16.5)(10) - (0.7)(246) = 150
Dy = (0.5)(246) - (16.5)(8) = -18
Finally, we can calculate the values of x and y:
x = Dx / D = 150 / (-1.6) = -93.75
y = Dy / D = -18 / (-1.6) = 11.25
However, it doesn't make sense to have negative quantities of bottles. So, we can round the values of x and y to the nearest whole number:
x ≈ -94 (rounded to -94)
y ≈ 11 (rounded to 11)
Therefore, based on the calculation, it appears that Matti had approximately 94 bottles of 0.5 litres and 11 bottles of 0.7 litres in the last patch of moonshine that he sold.
for such more question on litres
https://brainly.com/question/27877215
#SPJ8
Question
Matti is making moonshine in the woods behind his house. He’s selling the moonshine in two different sized bottles: 0.5 litres and 0.7 litres. The price he asks for a 0.5 litre bottle is 8€, for a 0.7 litre bottle 10€. The last patch of moonshine was 16.5 litres, all of which Matti sold. By doing that, he earned 246 euros. How many 0.5 litre bottles and how many 0.7 litre bottles were there? Solve the problem by using the determinant method (a.k.a. Cramer’s rule).
A gymnasium is 40 m long. Starting at one end lines are taped every 5 yd across the floor.
How many lines are taped across the floor?
Answers
Answer:
8 lines
Step-by-step explanation:
5 yards = 4.572 meters
40 m /4.572 = 8.7489063867
8 lines
how do put this 7+2x=11+5x
Answers
collect like terms
2x - 5x = 11 - 7
- 3x = 4
divide both sides
x = - 4/3
In alternative form: x = - 1 1/3
In decimal form: -1.333
write the equations of all the circles

Answers
The equation of a circle with center (a, b) and radius r is:
(x - a)^2 + (y - b)^2 = r^2
(x, y) represents any point on the circle
What is a circle?A circle is described as a shape consisting of all points in a plane that are at a given distance from a given point, the center.
The properties of the circle are as follows:
The circles are said to be congruent if they have equal radii.The diameter of a circle is the longest chord of a circle.Equal chords of a circle subtend equal angles at the centre.The radius drawn perpendicular to the chord bisects the chord.Learn more about properties of the circle at: https://brainly.com/question/4244936
#SPJ1
Divide 6x²y-12x⁴y+ 15x³y²-3x²y² by 3x²y
Answers
Answer:
\( \frac{6 {x}^{2}y - 12 {x}^{4} y + 15 {x}^{3} {y}^{2} - 3 {x}^{2} {y}^{2} }{3 {x}^{2}y } \\ \frac{2 \times 3 {x}^{2}y - 6 {x}^{2} 3 {x}^{2} y + 5xy3 {x}^{2} y - y3 {x}^{2} y}{3 {x}^{2}y } \\ cancel3 {x}^{2} y \: from \: all \: term \\ = \frac{2 - 6 {x}^{2} + 5x y - y }{1} \\ = 2 - 6 {x}^{2} + 5xy - y \\ thank \: you\)
How much cardboard is used in inches
5.375×8.625×1.625 are the dimensions
Answers
The amount of cardboard used is 138.3046875 square inches.
To find the amount of cardboard used, we need to calculate the surface area of the given dimensions.
The surface area of a rectangular prism can be found by multiplying the length, width, and height of the prism.
Surface Area = 2(length × width + width × height + height × length)
Plugging in the given dimensions:
Length = 5.375 inches
Width = 8.625 inches
Height = 1.625 inches
Surface Area = 2(5.375 × 8.625 + 8.625 × 1.625 + 1.625 × 5.375)
Simplifying the equation:
Surface Area = 2(46.328125 + 14.078125 + 8.74609375)
Surface Area = 2(69.15234375)
Surface Area = 138.3046875 square inches
Therefore, 138.3046875 square inches of cardboard were consumed.
for such more question on surface area
https://brainly.com/question/20771646
#SPJ8
A scalene triangle has one side that is 16 centimeters long and one side that is 5 centimeters long. Which value could be the perimeter of the triangle? 5
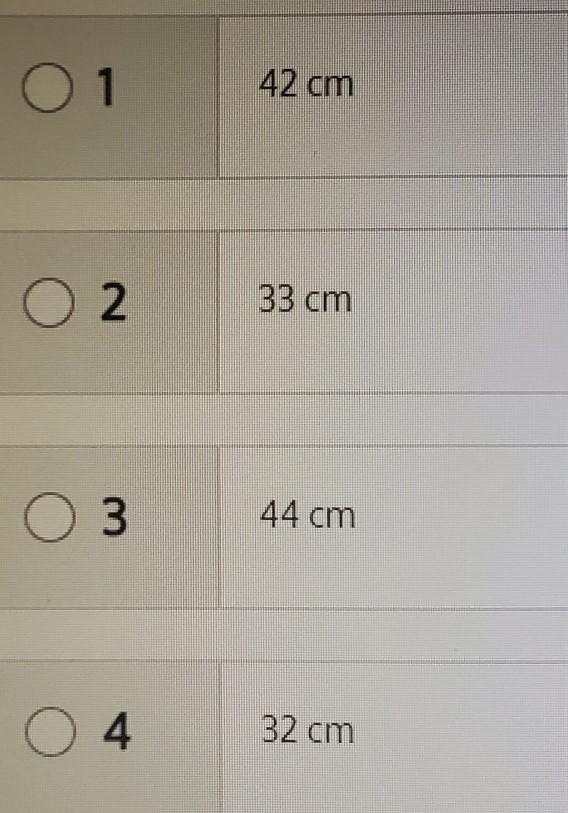
Answers
Since the triangle is scalene, then every side must have diferent size. The options are
\(\begin{gathered} 42-16-5=21 \\ 33-16-5=12 \\ 44-16-5=23 \\ 32-16-5=11 \end{gathered}\)Then, all the options can be the perimeter of the triangle
Graph the equation
y
=
x
2
−
12
x
+
35
y=x
2
−12x+35 on the accompanying set of axes. You must plot 5 points including the roots and the vertex.
Answers
X^2-12x+35=0
A=1 B=-12 C=35
B^2-4ac=(-12)^2 -4(1)(35)
=144 -140
=4
x=(-b+/- square root of b^2 -4ac) /over/ (2a)
Plug in the numbers
x=-(-12) sqr (-12)^2 4(1)(35) / (2)(1)
X=12 +/-sqr 4 / 2
Positive outcome
x=12 + sqr 4 / 2
x=12+2/2
x=7 <— this one
Negative outcome
x=12-2i/2
x=6-i
Vertex: (6,-1)
What is the square root of 10 plus 25 minus 5 times 20
Answers
Answer: √
10
−
75
Step-by-step explanation:
Answer:
463.245553
Step-by-step explanation:
3.16227766+25-5 times 20
Find the area of a rectangle with a length of 11.2 inches and a height of 9.4 inches
show your work
Please help
Answers
Answer: 105.28 inches
Find the range of f(x) = 5x - 4 for the domain = {2, 4, 6}]
Answers
Answer:
Step-by-step explanation:
For this question they are asking you to find y when x is {2, 4, and 6}
That means you need to plug 2,4, and 6 into the equation and solve.
For example:
f(x) = 5x - 4
f(2) = 5(2) - 4
f(2) = 10 - 4
f(2) = 6
f(x) = 5x - 4
f(4) = 5(4) -4
f(4) = 20 - 4
f(4) = 16
f(x) = 5x - 4
f(6) = 5(6) - 4
f(6) = 30 - 4
f(6) = 26
Answer:
6,16,26 is the answer
Step-by-step explanation:
The base of a right triangular prism is right angle triangle if the height of the prism is 12 cm and the longer side of the base is 5 cm while the shortest side is 3 cm then find A)The lateral surface area B)The total surface area
Answers
Answer:
A) 144 cm²;B) 156 cm².-------------------------------
The base is a right triangle with shortest side of 3 cm and hypotenuse of 5 cm.
Then, according to Pythagorean Theorem, its longer leg is:
\(\sqrt{5^2-3^2} =\sqrt{25-9} =\sqrt{16}=4 \cm\) Part AFind the lateral surface area:
LSR = Ph = (3 + 4 + 5)*12 = 12*12 = 144 cm²Part BFind the area of two triangle bases:
A = 2*(1/2)bh = 3*4 = 12 cm²Find the total surface area by adding up base area and lateral surface area:
TSA = 12 + 144 = 156 cm²Calculate f(8) should be a numerical value

Answers
Hey there!
f(x) = g(x) = h(x) = y
Since, you have the value of x (8), you can substitute it in the equation to make it easier to solve. We just have to find your f(x) value (also known as the y-value)
f(x) -0 -3 * x^2 - 2
f(x) = -3x^2 - 2
y = -3x^2 - 2
y = -3(8)^2 - 2
y = -3(8^2) - 2
y = -3(8 * 8) - 2
y = -3(64) - 2
y = -192 - 2
y = -194
Therefore, your answer should be:
f(x) = -194
Good luck on your assignment & enjoy your day!
~Amphitrite1040:)
2. A parallelogram must be a rhombus when its (2 pts)
(1) diagonals are perpendicular
(2) diagonals are congruent
(3) opposite sides are parallel
(4) opposite sides are congruent
Answers
A parallelogram must be a rhombus when its diagonals are perpendicular.
What is a rhombus?A rhombus is a quadrilateral that has all its four sides equal in length. The diagonals of the rhombus bisect each other at a right angle. Also, the opposite angles of a rhombus are equal in measure and opposite sides are parallel to each other.
Given that, a parallelogram is a rhombus,
According to the definition of a rhombus, we know that, The diagonals of the rhombus bisect each other at a right angle.
Hence, the true statement is A parallelogram must be a rhombus when its diagonals are perpendicular.
For more references on rhombus, click;
https://brainly.com/question/27870968
#SPJ2
21
The cash price for a boiler is £2000
Customers can pay the cash price or pay monthly.
Cash Price
Pay Monthly
£2000
60 monthly payments of £40
Work out the percentage increase from the cash price when paying monthly
Maths
Answers
The percentage rise from the cash price when paying monthly is 20%.
To calculate the percentage increase from the cash price when paying monthly, we need to compare the total amount paid when paying monthly with the cash price.
The cash price for the boiler is £2000. When paying monthly, the customer makes 60 payments of £40 each. Total amount paid monthly = 60 * £40 = £2400. To find the percentage increase, we can use the following formula:
Percentage increase = ((Total amount paid monthly - Cash price) / Cash price) * 100.
Substituting the values, we get:
Percentage increase = ((£2400 - £2000) / £2000) * 100 = (£400 / £2000) * 100 = 20%.
Therefore, the percentage increase from the cash price when paying monthly is 20%. This means that the customer pays 20% more than the cash price over the 60-month period when opting for monthly payments.
To know more about cash price, refer here :
https://brainly.com/question/1114543#
#SPJ11
an inlet pipe on a swimming pool can be used to fill the pool in 26 hours. the drain pipe can be used to empty the pool in 30 hours. if the pool is 25 filled and then the inlet pipe and drain pipe are opened, how many more hours would it take to fill the pool? round your answer to two decimal places, if needed.
Answers
The total time required to fill the pool completely as per the inlet and drain pipe capacity is given by 146.25 hours.
Let's assume that the capacity of the pool is 1 unit .
The inlet pipe can fill the pool at a rate of 1/26 units per hour.
The drain pipe can empty it at a rate of 1/30 units per hour.
When both pipes are open,
The net rate of filling is the difference between the rate of filling and the rate of emptying,
Net rate = Rate of filling - Rate of emptying
⇒Net rate = 1/26 - 1/30
⇒Net rate = (30 -26 )/780
⇒Net rate = (4)/780
⇒Net rate = 1/195 units per hour
Since the pool is already 25% filled.
This implies,
It still needs to be filled by another 0.75 units.
The time required to fill the pool by 0.75 units at a net rate of 1/195 units per hour can be found using the formula,
Time = Amount of filling needed / Net rate
⇒Time = 0.75 / (1/195)
⇒Time = 146.25 hours
Therefore, the total time taken to fill the pool completely would take another 146.25 hours.
learn more about time here
brainly.com/question/26428266
#SPJ4
Write the slope intercept form of the equation of each line given the slope and y intercept

Answers
Answer:
Heyy, could you please take a screenshot? It'll be so much easier to see haha. Try Snipping tool if you have Windows, and Command + Shift + 4 for screenshot on Mac. Then I can answer.
Step-by-step explanation: