Answers
Answer:x=37
Step-by-step explanation:
Related Questions
The coordinates for a quadrilateral are A(3, 5), B(7, 5), C(8, 3) and D(4, 3). Determine the type of quadrilateral.
Group of answer choices
Rectangle
Parallelogram
Square
Rhombus
Answers
Answer:
Rhombus
Step-by-step explanation:
Just graph on the coordinate grid.
Answer:
Parallelogram
Step-by-step explanation:
You have to put the coordinates in a Cartesian diagram and connecting the points you will find the figure
the reciprocal of 5 and 4/9
Answers
Answer:
1/5 and 9/4
Step-by-step explanation:
Reciprocal is basically the vertically flipped version of the original number. To find the reciprocal, rewrite the numbers in fractions and then swap the numerator and the denominator. So 5/1 becomes 1/5, 4/9 becomes 9/4.
What is a expression? What is a mathematical equation? What is Equation Modelling? What is the reciprocal of a number?
A mathematical expression is made up of terms (constants and variables) separated by mathematical operators. A mathematical equation is used to equate two expressions. Equation modelling is the process of writing a mathematical verbal expression in the form of a mathematical expression for correct analysis, observations and results of the given problem. The reciprocal of a number [x] is given by [1/x].
We have the following numbers -
5 and 4/9
We can write -
x = 5
y = 4/9
So, the reciprocal of [x] would be [1/x]. Therefore, the reciprocal of 5 will be 1/5.
The reciprocal of [y] would be [1/y]. Therefore, the reciprocal of 4/9 will be 9/4.
Therefore -
the reciprocal of 5 will be 1/5. the reciprocal of 4/9 will be 9/4.
To solve more questions on Equations, Equation Modelling and Expressions visit the link below -
brainly.com/question/14441381
#SPJ2
what is the product of each equation?
\(\left(3a^{2}b^{4}\right)\left(-8ab^{3}\right)\)
\(\left(3a^{2}b^{7}\right)\left(5a^{3}b^{8}\right)\)
\(\left(-2d^{2}+s\right)\left(5d^{2}-6s\right)\)
\(\left(3x-6\right)\left(2x^{2}-7x+1\right)\))
\(\left(7x^{2}y^{3}\right)\left(3x^{5}y^{8}\right)\)
\(\left(y^{2}+3y+7\right)\left(8y^{2}+y+1\right)\)
\(\left(4s+2\right)\left(5s^{2}+10s+3\right)\)
Answers
The solution to the products of exponents is as follows;
1) -24a³b⁷
2) 15a⁵b¹⁵
3) -10d⁴ + 17sd² - 6s²
4) 6x³ - 33x² + 45x - 6
5) 21x⁷y¹¹
6) 8y⁴ + 25y³ + 60y² + 10y + 7
7) 20s³ + 50s² + 32s + 6
How to find product of exponents?The Product of Powers Property of exponents states that when we multiply two powers with the same base, we add the exponents.
1) (3a²b⁴) * (-8ab³)
= -24a³b⁷
2) (3a²b⁷) * (5a³b⁸)
= 15a⁵b¹⁵
3) (-2d² + s)(5d² - 6s)
Expanding the bracket to get;
(-10d⁴ + 5sd² + 12sd² - 6s²)
= -10d⁴ + 17sd² - 6s²
4) (3x - 6) * (2x² - 7x + 1)
= 6x³ - 33x² + 45x - 6
5) (7x²y³) * (3x⁵y⁸)
= 21x⁷y¹¹
6) (y² + 3y + 7) * (8y² + y + 1)
= 8y⁴ + 25y³ + 60y² + 10y + 7
7) (4s + 2) * (5s² + 10s + 3)
= 20s³ + 50s² + 32s + 6
Read more about product of Exponents at; https://brainly.com/question/847241
#SPJ1
Solve for x:
4(x + 4) = 6(x - 2)
O A. x = 9
B. x = 14
O C. x = 8
D. x = 1
Answers
Answer:
x = 14
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDASAlgebra I
Equality PropertiesStep-by-step explanation:
Step 1: Define equation
4(x + 4) = 6(x - 2)
Step 2: Solve for x
Distribute: 4x + 16 = 6x - 12Subtract 4x on both sides: 16 = 2x - 12Add 12 on both sides: 28 = 2xDivide 2 on both sides: 14 = xRewrite: x = 14Step 3: Check
Plug in x to verify it's a solution.
Substitute: 4(14 + 4) = 6(14 - 2)Add/Subtract: 4(18) = 6(12)Multiply: 72 = 72And we have our final answer!
Answer: 14 = x
Step-by-step explanation: Start by distributing through the parenthses
on each side of the equation to get 4x + 16 = 6x - 12.
Now move your x's to the right and numbers
to the left and you get 28 = 2x.
Divide both sides by 2 and 14 = x.
PLEEAASSEE help i will give brainliest

Answers
Answer:
e) 17 miles
Step-by-step explanation:
15^2+8^2=289
\(\sqrt{289\)=17
NEED ANSWER ASAP PORFAVOR WILL GIVE BRAINLIEST

Answers
Answer:
20 mph
Step-by-step explanation:
Given that a dolphin swam 7 1/2 miles in 3/8 hour, you want its average speed in miles per hour.
Average speedThe average speed is the ratio of distance to time:
speed = distance/time
speed = (7 1/2 mi)/(3/8 h) = (15/2)(8/3) mi/h = 20 mi/h
The dolphin's average speed was 20 miles per hour.
k means algorithm terminates when mcq
Answers
The K-Means algorithm terminates when. a user-defined minimum value for the summation of squared error differences between instances and their corresponding cluster center is seen.
The K-Means algorithm terminates when
A) a user-defined minimum value for the summation of squared error differences between instances and their corresponding cluster center is seen.
B) the cluster centers for the current iteration are identical to the cluster centers for the previous iteration.
C) the number of instances in each cluster for the current iteration is identical to the number of instances in each cluster of the previous iteration.
D) the number of clusters formed for the current iteration is identical to the number of clusters formed in the previous iteration.
Learn more about k means algorithm here :
https://brainly.com/question/15862564
#SPJ4
In a survey, 200 college students were asked whether they live on campus and if they own a car. Their responses are summarized in the following table below.

Answers
If in a survey, 200 college students were asked whether they live on campus and if they own a car, 55% of college students in the survey don't own a car.
To find the percent of college students who don't own a car, we need to add up the number of students who don't own a car and divide it by the total number of students in the survey. In this case, the total number of students in the survey is 200.
From the table, we can see that there are 88 students who live on campus and don't own a car, and 22 students who don't live on campus and don't own a car. So the total number of students who don't own a car is 88 + 22 = 110.
To find the percentage, we divide the number of students who don't own a car by the total number of students in the survey and then multiply by 100 to get the percentage:
Percentage of students who don't own a car = (110/200) x 100% = 55%
When working with percentages, we need to divide the number we are interested in by the total and then multiply by 100 to get the percentage.
To learn more about survey click on,
https://brainly.com/question/26551559
#SPJ1
Aaron took a taxi from his house to the airport. The taxi company charged a pick-up fee of $2 plus $3.50 per mile. The total fare was $58, not including the tip. Which equation could be used to determine xx, the number of miles in the taxi ride?
Answers
Answer:
58 = 3.5x + 2
Step-by-step explanation:
Since $3.50 is charged for every mile, we multiply x by 3.5 like this: 3.5x
$2 is already added on as a free so + 2
$58 is the total amount of money for all of the charges including the per mile and pick-up fee.
This was we can solve for the number of miles, x
58 = 3.5x + 2
- 2 - 2
56 = 3.5x
56/3.5 = 3.5x/3.5
x = 16
The taxi drove a total of 16 miles
What is the area of this figure?
3 cm
9 cm
5 cm
23 cm
6 cm
11 cm
8 cm
19 cm

Answers
Answer:
218 cm²
Step-by-step explanation:
= high × wide
= 9 × 2
= 18
= 6 × (5+3)
= 6 × 8
= 48
= 8 × (11+5+3)
= 8 × 19
= 152
area throughout
= 152 + 48 + 18
= 218 cm²
what is the area of the triangle? Round answers the nearest tenth.

Answers
Answer:
28.8 yd^2
Step-by-step explanation:
Area of triangle = (1/2) · b · h
Base = 9 yd
Height = 6.4 yd
We take
(1/2) · 9 · 6.4 = 28.8 yd^2
So, the area of the triangle is 28.8 yd^2
Need Help ASAP
Formula 1 can be written alternatively as formula 2. Use algebra to show your steps how formula 1 can be manipulated to create formula 2.
Formula 1:
\(f(n)=\left\\ ({\sqrt[{12}]{2}}\,\right)^{n-49}\times 440\,{\text{Hz}}\,}\)
Formula 2:
\(f(n) = 440 (2)^{\frac{n-49}{12} }\)
Answers
Answer:
Steps are shown
Step-by-step explanation:
Exponent Rules
We need to recall this fundamental rule for exponents:
\(\displaystyle \sqrt[n]{a^m}=a^{m/n}\)
We are given the expression:
\(f(n)=\left ({\sqrt[{12}]{2}}\,\right)^{n-49}\times 440\,{\text{Hz}}\)
We'll use algebra and the above rule to manipulate the expression.
First, get rid of the unit Hz and move the coefficient 440 to the left:
\(f(n)=440\left ({\sqrt[{12}]{2}}\,\right)^{n-49}\)
Now we convert the radical into an exponent form:
\(\displaystyle \left ({\sqrt[{12}]{2}}\,\right)^{n-49}=(2)^{\frac{n-49}{12}}\)
Substitute:
\(f(n)=440\left ({\sqrt[{12}]{2}}\,\right)^{n-49}=440~(2)^{\frac{n-49}{12}}\)
This is the very same expression in formula 2, as required.
Solve for x:
(a) 4x - 21 = 5 - 9x
Answers
Answer:
X = 2
Step-by-step explanation:
First we'll need to simplify this equation:
Add 9x on both sides:
13x - 21 = 5
Add 21 on both sides:
13x = 26
Divide 26/13
26/13 = 2
X=2
(You can check this yourself by plugging x into the equation)
can someone please help thank you

Answers
Answer:
I'm sorry your paper is not clear please retake the picture and again attached it
Step-by-step explanation:
the function f is defined by f(x)=150/x-z where z is a constant. find z if the value of f at x=1/5 is equal to 250
Answers
Answer:
z=500
Step-by-step explanation:
since we know that the whole equation is equal to 250, we can substitute values in.
250=150/1/5 -z
250=750-z
-500=-z
z=500
The value of z for the function f(x)=150/x-z is z=500.
What is an expression?The mathematical expression combines numerical variables and operations denoted by addition, subtraction, multiplication, and division signs.
Mathematical symbols can be used to represent numbers (constants), variables, operations, functions, brackets, punctuation, and grouping. They can also denote the logical syntax's operation order and other properties.
Given that the function f is defined by f(x)=150/x-z where z is a constant. The value of the function at x = 1/5 is 250.
The value of the constant z will be calculated as,
The whole equation is equal to 250, we can substitute values in.
250=150/1/5 -z
Simplify the equation and solve for the value of z,
250=750-z
-500=-z
z=500
Therefore, the value of z for the function f(x)=150/x-z is z=500.
To know more about an expression follow
https://brainly.com/question/24748644
#SPJ3
Evaluate the expression:
6² x (16 +19) — 10³
Answers
36×(35)-1000=1260-1000=260
What are the angle names given in the picture?
Plzzzz anyone answer I post question but no one answers them but plz anyone answer this time it’s a project and it’s due date is today plz helppp

Answers
Answer:
tbh there are quite a lot of possibilities
I'll just name the properties but not show which angle applies to it cos that's too time consuming
Step-by-step explanation:
vertically opposite angles
interior / exterior alternate angles
corresponding angles
angles on a straight line are supplementary
sketch the area represented by g(x). g(x) = x t2 dt 1
Answers
The area represented by g(x) is a triangular region with base 1 and height (7/3) x, where x is the variable along the horizontal axis. The resulting shape will be a right triangle with vertices at (0,0), (1,0), and (0, (7/3) x).
It seems like you are asking to sketch the area represented by the function g(x) given as the integral of x with respect to t from 1 to 2. However, there seems to be a typo in your question. I will assume that you meant g(x) = ∫[1 to x] t^2 dt. Please follow these steps to sketch the area represented by g(x):
1. Draw the function y = t^2 on the coordinate plane (x-axis: t, y-axis: t^2).
To sketch the area represented by g(x) = x t2 dt 1, we first need to evaluate the definite integral. Integrating x t2 with respect to t gives us (1/3) x t3 + C, where C is the constant of integration. Evaluating this expression from t=1 to t=2 gives us (1/3) x (2^3 - 1^3) = (7/3) x.
2. Choose an arbitrary x-value between 1 and 2 (e.g., x = 1.5).
3. Draw a vertical line from the x-axis to the curve of y = t^2 at x = 1.5. This line represents the upper limit of the integral.
4. Draw another horizontal axis from the x-axis to the curve of y = t^2 at x = 1. This line represents the lower limit of the integral.
5. The area enclosed by the curve y = t^2, the x-axis, and the vertical lines at x = 1 and x = 1.5 represents the area for the given value of x.
In conclusion, the area represented by g(x) = ∫[1 to x] t^2 dt can be sketched by plotting the curve y = t^2, choosing a specific x-value between 1 and 2, and then finding the enclosed area between the curve, x-axis, and the vertical lines at x = 1 and x = chosen x-value.
Learn more about horizontal axis:
brainly.com/question/29774083
#SPJ11
What is the area of the triangle?
8
10
6
units
2
IF U GET THE ANSWER THABK YOU AO MUCH
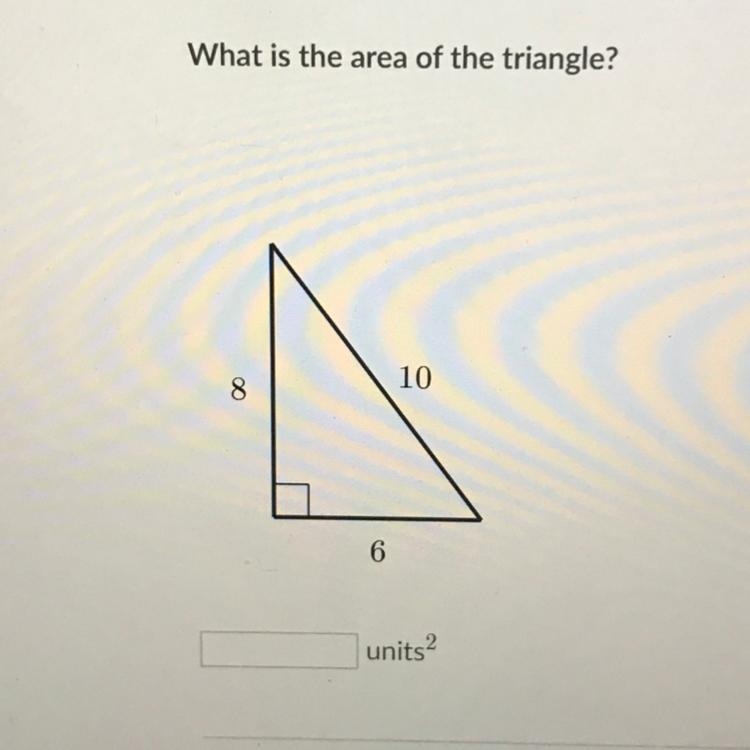
Answers
Answer:
24
Step-by-step explanation:
multiply base x height
HELLOOOOO CAN ANYBODY HELP

Answers
The function can be represented as follows;
(s + t)(x) = 5x + 5
(s - t)(x) = -3x - 1
(s.t)(x) = 4x + 5
How to solve functions?Function can be solved by using techniques of substitution.
s(x) = x + 2
t(x) = 4x + 3
Therefore,
(s + t)(x) = s(x) + t(x)
s(x) + t(x) = x + 2 + 4x + 3
s(x) + t(x) = x + 4x + 2 + 3
s(x) + t(x) = 5x + 5
(s - t)(x) = s(x) - t(x)
s(x) - t(x) = x + 2 - (4x + 3)
s(x) - t(x) = x + 2 - 4x - 3
s(x) - t(x) = x - 4x + 2 - 3
s(x) - t(x) = -3x - 1
(s.t)(x) = s(t(x))
s(t(x)) = (4x + 3) + 2
s(t(x)) = 4x + 3 + 2
s(t(x)) = 4x + 5
learn more on function here: https://brainly.com/question/12961756
#SPJ1
1. 1. Under a dilation
of scale factor 2 with the center at the origin, if S (6, 7), what will
be the coordinates of the point S'?
2. What is the scale factor of the group dilation (with center at the origin) if point E (5,3)
becomes E' (15,9)?
3. Under a dilation of scale factor 5 with the center at the origin, if M (3,6), what will be
the coordinates of the point M'?
4. What is the scale factor of the dilation (with center at the origin) if point H (4,6)
becomes H' (24, 36)?
5. Under a dilation of scale factor 4 with the center at the origin, if J (2, 3), what will be
the coordinates of the point J'?
6. What is the scale factor of the dilation (with center at the origin) if point U (5,7)
becomes U' (25, 35)?
7. Under a dilation of scale factor 7 with the center at the origin, if K (5,6), what will be
the coordinates of the point K'?
8. What is the scale factor of the dilation (with center at the origin) if point A (4,5)
becomes A' (16, 20)?
Answers
2: 3
3:(15,30)
4: 6
5(8,12)
6:5
7:(35,42)
8:;
Which expression is equivalent to V-80?
O-4.5
O
-4./5;
4.5;
0
4.5
Answers
Answer:
Your answer is: 4v5i
Step-by-step explanation:
Hope this helped : )
What is the diameter of a circle with the equation (x – 4)2 + (y + 6)2 = 64?
a. 4
b. 8
c. 16
d. 64
Answers
Answer:
16Step-by-step explanation:
step one:
given data
we are given the equation of the circle as
\((x -4)2^ + (y + 6)^2 = 64\)----------------1
We know that the general equation for a circle is
\(( x - h )^2 + ( y - k )^2 = r^2\)--------------2
comparing the two equations above, we can immediately compare the term on the other side of the equality sign that is
r^2=64
square root both sides
r=√64
r=8
since the radius is 8, hence the diameter is
d=2
r= 2*8
=16
Answer:
C. 16
Step-by-step explanation:
Edge!
the perimeter of a rectangle is 62 m.
Answers
Answer:
c o n f u s i o n
Step-by-step explanation:
Uh... I dunno, sure, the perimeter of a rectangle is 62 m, I guess?
Assume there is a sample of n
1
=4, with the sample mean
X
1
=35 and a sample standard deviation of S
1
=4, and there is an independent sample of n
2
=5 from another population with a sample mean of
X
ˉ
2
=31 and a sample standard deviation S
2
=5. In performing the pooled-variance t test, how many degrees of freedom are there? There are degrees of freedom. (Simplify your answer.)
Answers
There are 7 degrees of freedom.
In performing the pooled-variance t test, the degrees of freedom can be calculated using the formula:
df = (n1 - 1) + (n2 - 1)
Substituting the given values:
df = (4 - 1) + (5 - 1)
df = 3 + 4
df = 7
Therefore, there are 7 degrees of freedom.
Learn more about degrees of freedom
brainly.com/question/32093315
#SPJ11
There are 7 degrees of freedom for the pooled-variance t-test.
To perform a pooled-variance t-test, we need to calculate the degrees of freedom. The formula for degrees of freedom in a pooled-variance t-test is:
\(\[\text{{df}} = n_1 + n_2 - 2\]\)
where \(\(n_1\)\) and \(\(n_2\)\) are the sample sizes of the two independent samples.
In this case, \(\(n_1 = 4\)\) and \(\(n_2 = 5\)\). Substituting these values into the formula, we get:
\(\[\text{{df}} = 4 + 5 - 2 = 7\]\)
In a pooled-variance t-test, we combine the sample variances from two independent samples to estimate the population variance. The degrees of freedom for this test are calculated using the formula \(df = n1 + n2 - 2\), where \(n_1\)and \(n_2\) are the sample sizes of the two independent samples.
To understand why the formula is \(df = n1 + n2 - 2\), we need to consider the concept of degrees of freedom. Degrees of freedom represent the number of independent pieces of information available to estimate a parameter. In the case of a pooled-variance t-test, we subtract 2 from the total sample sizes because we use two sample means to estimate the population means, thereby reducing the degrees of freedom by 2.
In this specific case, the sample sizes are \(n1 = 4\) and \(n2 = 5\). Plugging these values into the formula gives us \(df = 4 + 5 - 2 = 7\). Hence, there are 7 degrees of freedom for the pooled-variance t-test.
Therefore, there are 7 degrees of freedom for the pooled-variance t-test.
Learn more about t-test
https://brainly.com/question/13800886
#SPJ11
Triangle HIJ, with vertices H(5,2), I(8,5), and J(3,9), is drawn inside a rectangle, as shown below.
Answers
The calculated area of the triangle is 13.5 square units
How to calculate the area of the triangle?From the question, we have the following parameters that can be used in our computation:
H(5,2), I(8,5), and J(3,9)
The area of the triangle in square units is calculated as
Area = 1/2 * |x₁y₂ - x₂y₁ + x₂y₃ - x₃y₂ + x₃y₁ - x₁y₃|
Substitute the known values in the above equation, so, we have the following representation
Area = 1/2 * |5 * 5 - 8 * 2 + 8 * 9 - 3 * 5 + 3 * 2 - 5 * 9|
Evaluate the sum and the difference of products
Area = 1/2 * 27
So, we have
Area = 13.5
Hence, the area of the triangle is 13.5 square units
Read more about area at
brainly.com/question/24487155
#SPJ1
Question
Triangle HIJ, with vertices H(5,2), I(8,5), and J(3,9), is drawn inside a rectangle, as shown below.
Calculate the area of the triangle
Given g(x) = 2x - 4, solve for x when g(x) = 0
Answers
Answer:
2
Step-by-step explanation:
2×2=4 4-4=0 so the answer is 2
Answer:
2
Step-by-step explanation:
g(x)=2x-4
x=? when g(x)=0
we know,
g(x)=2x-4
0=2x-4
4=2x
x=4/2
x=2#
A recipe calls for 1/2 cup of flour for every 8 teaspoons of milk.How much flour should be used for 4 teaspoons of milk?
Answers
Answer:
I think it's probably 1/4
Step-by-step explanation: It's probably 1/4 since you are really only taking away both of the ones and then dividing 2 and 8 that equals 4 so then you add the only 1 of the the ones and then you get 1/4
Help! ∠A=? Round to the nearest hundredths.
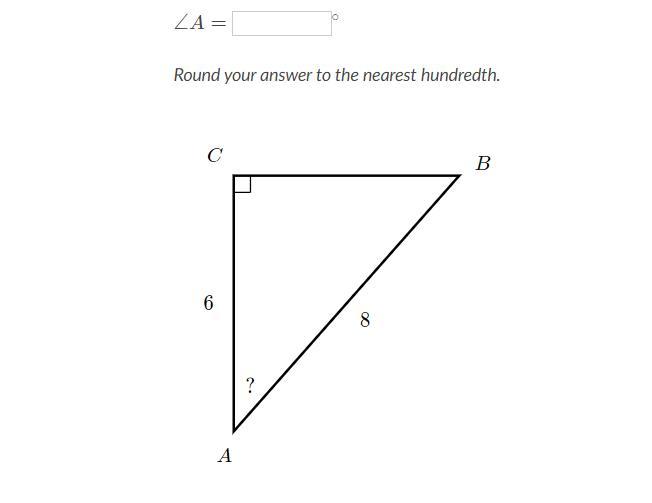
Answers
Hi there, here's your answer:
So given in the question is a right angled triangle, ΔABC, right angled at C
Also given AC = 6 units, AB = 8 units
To find, ∠A
We know that cosФ = \(\frac{adj}{hyp}\)
And \(\frac{6}{8} = \frac{2}{3} = 0.67\)
Therefore, the angle measure of ∠A will be 47.93°
Determine the angle between the two lines with equations 4x - 5y = 11 and 2x + 3y = 7.
Answers
Answer:
The angle between the two lines is 72.35° ⇒ to the nearest hundredth
Step-by-step explanation:
The angle between the two lines is the difference between their angles with the positive part of the x-axis (Ф = Ф\(_{2}\) - Ф\(_{1}\)) The slope of the line equal to the tangent of the angle between the line and the positive part of the x-axis (m = tan Ф)The slope of the line whose equation is ax + by = c is m = \(\frac{-a}{b}\)∵ The equation of the first line is 4x - 5y = 11
∴ a = 4 and b = -5
→ By using the 3rd rule of the slope above
∵ m\(_{1}\) = \(\frac{-4}{-5}\) = \(\frac{4}{5}\)
∴ m\(_{1}\) = 0.8
→ By using the 2nd rule above
∵ tan Ф\(_{1}\) = 0.8
∴ Ф\(_{1}\) = \(tan^{-1}\)(0.8)
∴ Ф\(_{1}\) = 38.66° ⇒ to the nearest hundredth
∵ The equation of the first line is 2x + 3y = 7
∴ a = 2 and b = 3
→ By using the 3rd rule of the slope above
∵ m\(_{2}\) = \(\frac{-2}{3}\)
∴ m\(_{2}\) = \(-\frac{2}{3}\)
→ By using the 2nd rule above
∵ tan Ф\(_{2}\) = \(-\frac{2}{3}\)
∴ Ф\(_{2}\) = \(tan^{-1}\)( \(-\frac{2}{3}\))
∴ Ф\(_{2}\) = -33.69° ⇒ to the nearest hundredth
→ By using the 1st rule above
∵ Ф = -33.69 - 38.66
∴ Ф = -72.35°
→ Ignore the negative sign
∴ The angle between the two lines is 72.35° ⇒ to the nearest hundredth
V.I.N:
You can use this rule to find the angle between 2 lines tan Ф = I\(\frac{m_{2}-m_{1}}{1+m_{1}.m_{2}}\)I
