Which capital letters have one or more lines of symmetry?
A) X
B) Z
C) H
D) C
Answers
Answer:
h has 4 lines x has 2 z has 3 c has none
Step-by-step explanation:
Related Questions
find all values of x such that (6, x, −11) and (5, x, x) are orthogonalfind all values of x such that (6, x, −11) and (5, x, x) are orthogonal
Answers
The values of x that make the vectors (6, x, -11) and (5, x, x) orthogonal are x = 5 and x = 6.
To find all values of x such that (6, x, -11) and (5, x, x) are orthogonal, we will use the dot product of the two vectors. Two vectors are orthogonal if their dot product is zero.
2 vectors are called orthogonal if they are perpendicular to each other, and after performing the dot product analysis, the product they yield is zero.
In mathematical terms, the word orthogonal means directed at an angle of 90°. Two vectors u,v are orthogonal if they are perpendicular, i.e., they form a right angle, or if the dot product they yield is zero.
1: Write down the two vectors.
Vector A = (6, x, -11)
Vector B = (5, x, x)
2: Calculate the dot product of the two vectors.
A · B = (6 * 5) + (x * x) + (-11 * x)
3: Set the dot product equal to zero, as the vectors are orthogonal.
30 + x^2 - 11x = 0
4: Rearrange the equation to solve for x.
x^2 - 11x + 30 = 0
5: Factor the quadratic equation.
(x - 5)(x - 6) = 0
6: Solve for x.
x = 5 or x = 6
Learn More About Vector's: https://brainly.com/question/3184914
#SPJ11
The graph represents a mechanic’s labor costs for a given number of hours of car repair. A graph titled Car Repairs. The horizontal axis shows Labor Time (hours) numbered 0.25 to 2.5, and the vertical axis shows Labor Costs (dollars), numbered 25 to 250. The line remains constant at $50 dollars over 1 hour, then increases sharply. The line remains at 50 dollars from 0 to 1 hour, then move upward to end at 175 dollars at 2.5 hours.
Answers
Answer:
A: All repairs requiring 1 hour or less have the same labor cost.
Step-by-step explanation:
Answer:
A: All repairs requiring 1 hour or less have the same labor cost.
Step-by-step explanation: all right!
The measure of two remote interior angles of a triangle are x - 10 and 4x + 4 The exterior angle of the triangle measures 3x + 54 Solve for the measure of the exterior angle .
Answers
The measure of the exterior angle of the triangle is 144 degrees.
How to solve angles of a triangle?The exterior angle theorem states that the measure of an exterior angle is equal to the sum of the measures of the two remote interior angles of the triangle.
Therefore, the measure of the two remote interior angles of a triangle are x - 10 and 4x + 4. The exterior angle of the triangle measures 3x + 54 .
Let's solve for the exterior angle.
x - 10 + 4x + 4 = 3x + 54
5x - 6 = 3x + 54
5x - 3x = 54 + 6
2x = 60
x = 60 / 2
x = 30
Therefore,
exterior angle = 3x + 54 = 3(30) + 54 = 90 + 54 = 144 degrees
learn more on triangle here:https://brainly.com/question/11379452
#SPJ1
Quick algebra 1 question for 50 points!
Only answer if you know the answer, Tysm!

Answers
Answer:
No this is not a function because the x-values repeat. In a function you can have the the output duplicate but not the input. The input at 3 has duplicates s o this is not a function.
Step-by-step explanation:
Definition
A relation is called to be a function if every domain has an unique range
f(x)=yHere
f(3)=-9,4As
f(3) has 2 corresponding values it's not a function
Elise said that 0.1 equals 1% complete the explanation of her mistake
Answers
what are the odds in favor of rolling twl number cubes and having a 7 on the first roll and doubles on the second roll?
please give an explanation

Answers
In a picture with 1st number cube as 1 to 6 numbers and the 2nd number cube as 1 to 7. the probability of obtaining the number 7 is \(\frac{1}{7}\).
Given that,
There is a picture with 1st number cube as 1 to 6 numbers and the 2nd number cube as 1 to 7.
We have to calculate the probability of getting sum of 7.
That is,
Total possibility =Number of the 1st number cube \(\times\) number of the 2nd number cube.
=6\(\times\)7
=42
The probability of getting sim of 7 is
Check in the row where the 7 is there and count it
From the picture we can say 7 in is 6 rows.
So, =\(\frac{6}{42}\\\)
=\(\frac{1}{7}\)
Therefore, the probability of obtaining the number 7 is \(\frac{1}{7}\).
To learn more about cubes visit: https://brainly.com/question/28134860
#SPJ1
*WILL MARK BRAINLIEST* The triangle below is isosceles. Find the length of side xx in simplest radical form with a rational denominator.

Answers
Answer: 5sqrt2, 10sqrt2/2
Step-by-step explanation:
The isosceles triangle, or 45-45-90 rule states that the hypotenuse is x × square root of 2.
Divide the hypotenuse, 10, by sqrt 2 to get 5sqrt2
However , if you're looking to keep it in fraction form, you will need to rationalize the denominator. Multiply the numerator and denominator to get the fraction, 10sqrt2/2
The graph of FX), shown below, has the same shape as the graph ofG(X) = x2, but it is shifted to the left 3 units. What is its equation?FX) ----A. F(x) = x² + 3B. FX) = (x - 3)2C. FX) = x2.3D. Rx) = (x + 3)?

Answers
We can represent the horizontal shift of a quadratic equation by adding or subtracting the constant h to the function
\(\begin{gathered} f(x)=a(x-h)^2+k \\ \text{where} \\ h\text{ is the horizontal shift} \end{gathered}\)\(\begin{gathered} \text{The function }f(x)\text{ has a default values of} \\ a=1 \\ h=0 \\ k=0 \\ \\ \text{A shift to the left of 3 units means that we will have }h=-3\text{ that means} \\ \\ F(x)=(x-(-3))^2 \\ \\ \text{Simplify},\text{ and we get} \\ F(x)=(x+3)^2 \end{gathered}\)determine whether the pair of planes is parallel, orthogonal, or neither. let g be the plane −9x 2y−5z=48 and h be the plane 2x−y−4z=−28.
Answers
The pair of planes are neither parallel nor orthogonal.
HOW TO DETERMINEThe pair of planes given, g:
-9x + 2y - 5z = 48 and h:
2x - y - 4z = -28, are neither parallel nor orthogonal.
To determine this, we can find the normal vectors of each plane.
The normal vector of g is <9,2,-5> and the normal vector of h is <2,-1,-4>.
Since the normal vectors are not parallel or perpendicular to each other, the planes are neither parallel nor orthogonal.
Learn more about orthogonal at
https://brainly.com/question/2292926
#SPJ11
Which graph represents the solution set of the inequality x + 2 greater-than-or-equal-to 6 A number line goes from negative 9 to positive 9. A solid circle appears on positive 3. The number line is shaded from positive 3 through negative 9. A number line goes from negative 9 to positive 9. An open circle appears at positive 3. The number line is shaded from positive 3 through positive 9. A number line goes from negative 9 to positive 9. A closed circle appears at positive 4. The number line is shaded from positive 4 through positive 9. A number line goes from negative 9 to positive 9. An open circle appears at positive 4. The number line is shaded from positive 4 through negative 9.
Answers
Answer:
C. A number line goes from negative 9 to positive 9. A closed circle appears at positive 4. The number line is shaded from positive 4 through positive 9Step-by-step explanation:
Given inequality:
x + 2 ≥ 6Solution is:
x ≥ 6 - 2x ≥ 4Since the number line is restricted to -9, + 9 interval, the solution will appear as shaded part to the right from 4 through 9, where 4 is included point.
Correct answer choice is C
Urgent! Find the length of the tangent segment AC given circle B below
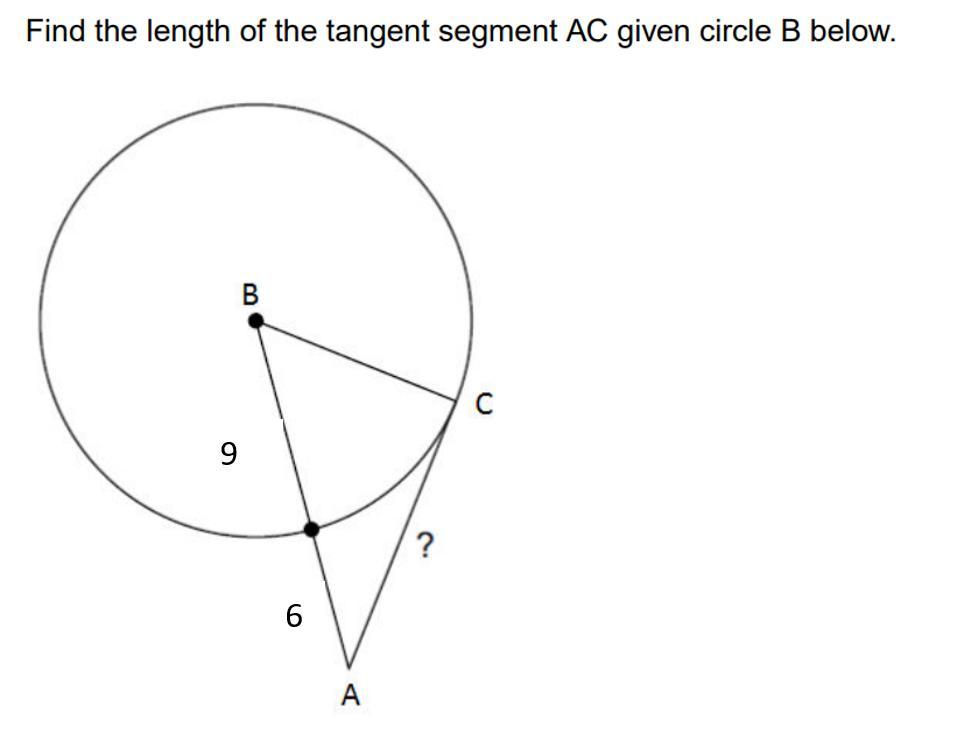
Answers
Answer:
AC ≈ 12
Step-by-step explanation:
the angle between the tangent AC and the radius BC is 90°
then Δ ABC is right
note that BC = 9 ( radius of circle )
using Pythagoras' identity in the right triangle
AC² + BC² = AB²
AC² + 9² = (9 + 6)² = 15²
AC² + 81 = 225 ( subtract 81 from both sides )
AC² = 144 ( take square root of both sides )
AC = \(\sqrt{144}\) = 12
Sharkey's Fun Center contains a number of electronic games as well as a miniature golf course and various rides located outside the building. Paul Sharkey, the owner, would like to construct a water slide on one portion of his property. Mr. Sharkey gathered the following information about the slide: a. Water slide equipment could be purchased and installed at a cost of $525,000. According to the manufacturer, the slide would be usable for 12 years after which it would have no salvage value. b. Mr. Sharkey would use straight-line depreciation on the slide equipment. c. To make room for the water slide, several rides would be dismantled and sold. These rides are fully depreciated, but they could be sold for $127.750 to an amusement park in a nearby city. d. Mr. Sharkey concluded that about 50,000 more people would use the water slide each year than have been using the rides. The admission price would be $5.00 per person (the same price the Fun Center has been charging for the old rides). e. Based on experience at other water slides, Mr. Sharkey estimates that annual incremental operating expenses for the slide would be: salaries, $95,000; insurance, $5,800; utilities, $14,600; and maintenance, $11,400. Required: 1. Prepare an income statement showing the expected net operating income each year from the water slide. 2-a. Compute the simple rate of return expected from the water slide. 2-b. Based on the above computation, would the water slide be constructed if Mr. Sharkey requires a simple rate of return of at least 13% on all investments? 3-a. Compute the payback period for the water slide. 3-b. If Mr. Sharkey accepts any project with a payback period of five years or less, would the water slide be constructed?
Answers
1. The expected net operating income each year from the water slide is $238,150.
2. The simple rate of return expected from the water slide is 12.5%.
Let us discuss in a detailed way:
⇒ To calculate the net operating income, we need to consider the additional revenue from increased attendance and subtract the incremental operating expenses.
The additional attendance from the water slide is estimated to be 50,000 people per year. With an admission price of $5.00 per person, the additional revenue would be $250,000 ($5.00 x 50,000).
The incremental operating expenses for the water slide amount to $126,800 ($95,000 + $5,800 + $14,600 + $11,400).
Therefore, the expected net operating income each year is $238,150 ($250,000 - $126,800).
⇒ The simple rate of return is calculated by dividing the average annual net income by the initial investment cost and expressing it as a percentage.
The average annual net income is calculated by subtracting the annual operating expenses from the additional revenue generated. In this case, the average annual net income is $113,350 ($238,150 - $124,800).
The initial investment cost is $525,000.
Using these values, the simple rate of return is 21.6% ($113,350 / $525,000).
To know more about simple rate of return, refer here:
https://brainly.com/question/17164328#
#SPJ11
What is the rule for the function that is graphed?
y = 2 x + 2
y = 2 x – 3
y = 3 x + 1
y = 3 x – 4

Answers
Answer: y = 3x — 2
Step-by-step explanation:
What was Art’s total deposit?
a.
$1,701.23
b.
$1,545.83
c.
$1,856.63
d.
$1516.35
Answers
Answer:
B
$1,545.83
Step-by-step explanation:
Which point gives the y-intercept of f(x) = - x2 + 4x - 3?
A) (-3,0)
B) (0,3)
C) (0.-3)
D) (3,0)

Answers
Answer:
The y intercept is (0,-3)
Step-by-step explanation:
The y intercept is when x =0
f(x) = - x^2 + 4x - 3
f(0) = 0 +0 -3
f(0) =-3
The y intercept is (0,-3)
Compare the leakage current ratio of a transistor under the following configurations? y = 1, n = 0.1, Pr = 0.35 V, VDD = 1 V, T = 300K, VTHo = 0.4 V (threshold voltage without DIBL and body effects). VDD VDD 0 0 킬 0.2 V Answer: 152 ×.
Answers
The answer to the question is 7
The leakage current ratio of a transistor can be determined by comparing the leakage current in different configurations. In this case, we are given the parameters y, n, Pr, VDD, T, and VTHo.
The leakage current ratio is the ratio of the leakage current in two different configurations. In this case, we need to compare the leakage current when VDD is 0 and 0.2 V.
Using the given parameters and the formula for the leakage current, we can calculate the leakage current for both configurations.
When VDD is 0, the leakage current is given by:
I_leakage = y * Pr * exp[(VTHo-VDD)/n*VT]
Plugging in the values, we get:
I_leakage(0) = 1 * 0.35 * exp[(0.4-0)/0.1*VT] = 7.79 × 10^-10 A
When VDD is 0.2 V, the leakage current is given by:
I_leakage = y * Pr * exp[(VTHo-VDD)/n*VT]
Plugging in the values, we get:
I_leakage(0.2) = 1 * 0.35 * exp[(0.4-0.2)/0.1*VT] = 5.11 × 10^-9 A
Therefore, the leakage current ratio is:
I_leakage(0.2)/I_leakage(0) = (5.11 × 10^-9)/(7.79 × 10^-10) = 6.56
Rounded to the nearest integer, the leakage current ratio is 7.
To learn more about leakage current : brainly.com/question/29545860
#SPJ11
35. The parallel sides of an isosceles trapezoid shown below are 20 centimeters long and 32 centimeters long, respectively . What is the area in square centimeters, of the trapezoid?
Answers
To find the area of an isosceles trapezoid, we need to know the lengths of the parallel sides and the height (or altitude) of the trapezoid.
In this case, we know that one parallel side is 20 centimeters long and the other parallel side is 32 centimeters long. However, we don't know the height of the trapezoid.
To find the height of the trapezoid, we can draw a line perpendicular to the parallel sides, creating two right triangles.
The height of the trapezoid is the hypotenuse of one of these right triangles, and we can use the Pythagorean theorem to find its length.
The legs of the right triangle are:
- Half of the difference between the parallel sides: (32 - 20) / 2 = 6
- The height of the trapezoid (which we'll call h)
Using the Pythagorean theorem, we can write:
h^2 = 6^2 + x^2
where x is the length of the height of the trapezoid.
Simplifying, we get:
h^2 = 36 + x^2
We still don't know the value of x, but we do know that the height of the trapezoid is perpendicular to the bases, so it forms a rectangle with the shorter base. Therefore, the height is also the length of the two sides of a right triangle with a hypotenuse of 20 (half of the shorter base).
Using the Pythagorean theorem again, we can write:
h^2 + 6^2 = 20^2
Simplifying, we get:
h^2 = 400 - 36
h^2 = 364
h ≈ 19.06
Now that we know the height of the trapezoid, we can use the formula for the area of a trapezoid:
Area = (base1 + base2) / 2 x height
Plugging in the values we know, we get:
Area = (20 + 32) / 2 x 19.06
Area ≈ 526.24 square centimeters
Therefore, the area of the isosceles trapezoid is approximately 526.24 square centimeters.
Answer:
260
Step-by-step explanation:
To find the area of an isosceles trapezoid, you need to know the lengths of the parallel sides (called bases) and the height (the perpendicular distance between the bases). The formula for the area of an isosceles trapezoid is: A = (1/2) * (a + b) * h, where A is the area, a and b are the lengths of the bases, and h is the height12
In your message, you have given the lengths of the bases as 20 cm and 32 cm, but you have not given the height. You need to measure or know the height to find the area. If you have the height, you can plug it into the formula and calculate the area. For example, if the height is 10 cm, then:
A = (1/2) * (a + b) * h A = (1/2) * (20 + 32) * 10 A = (1/2) * 52 * 10 A = 26 * 10 A = 260 cm^2
The area of the isosceles trapezoid is 260 square centimeters
How to convert 95 confidence z score?
Answers
The z-score associated with a 95% confidence level is approximately 1.96.
The z-score associated with a 95% confidence level is the value of the standard normal distribution that corresponds to an area of 0.95 to the left of the z-score.
Using a standard normal distribution table or calculator, we can find that the z-score associated with a 95% confidence level is approximately 1.96.
Therefore, if we want to calculate the z-score for a 95% confidence level, we can use the formula
z = invNorm(1 - α/2)
where α is the significance level (α = 0.05 for a 95% confidence level), and inv Norm is the inverse normal cumulative distribution function. Using this formula, we can calculate the z-score as:
z = inv Norm(1 - 0.05/2)
= inv Norm(0.975) ≈ 1.96
Therefore, the z-score is 1.96
Learn more about z-score here
brainly.com/question/15016913
#SPJ4
A windshield wiper is 45 cm long and
creates a central angle of 120° in one
wipe. what is the sector area?
Answers
The windshield sector area is 706.86 cm².
To calculate the sector area of the windshield wiper, we need to use the formula for the area of a sector of a circle. The formula is:
A = (θ/360°) x πr²
where A is the area of the sector, θ is the central angle of the sector in degrees, and r is the radius of the circle.
In this problem, we are given that the windshield wiper has a length of 45 cm, which means that the radius of the circle traced by the wiper is 45 cm/2 = 22.5 cm.
We are also given that the wiper creates a central angle of 120° in one wipe. Substituting these values into the formula, we get:
A = (120°/360°) x π(22.5 cm)²
A = (1/3) x π x (22.5 cm)²
A ≈ 706.86 cm²
Therefore, the sector area of the windshield wiper is approximately 706.86 square centimeters.
To learn more about sector area refer here:
https://brainly.com/question/16367606
#SPJ11
if i have one
mom then she dies how many moms do i have
Answers
Answer:
Step-by-step explanation:
1-1=0
Answer:You will have 0 moms.
Step-by-step explanation:
First you take 1 away from 1.
After that you get your answer of 0.
(ii) the position of a ball rolling in a straight line is given by x = 2.0 - 3.6 t 1.1 t 2 , where x is in meters and t in seconds.
Answers
The position of the ball at t = 2 seconds is -0.8 meters.
The position of a ball rolling in a straight line is given by the equation x = 2.0 - 3.6t + 1.1t^2, where x is the position in meters and t is the time in seconds. To find the position of the ball at a specific time, we can plug in the value of t into the equation and solve for x.
For example, if we want to find the position of the ball at t = 2 seconds, we can plug in 2 for t and solve for x:
x = 2.0 - 3.6(2) + 1.1(2)^2
x = 2.0 - 7.2 + 4.4
x = -0.8
Therefore, the position of the ball at t = 2 seconds is -0.8 meters.
Similarly, we can plug in any value of t into the equation to find the position of the ball at that specific time.
Learn more about Position
brainly.com/question/15668711
#SPJ11
Solve the following equation for. 1 a2 d2 d2 + 2 ℏ2 |E| = 0, Assume a standard trial solution = A exp(iB). (Use the following as necessary: a, E, , and ℏ. ) A = B = Find the allowed energies and angular momenta. (Use the following as necessary: a, , ℏ, and n, the quantum number. ) E =
Answers
To solve the given equation using the standard trial solution with quantum number, we substitute A exp(iB) for the wavefunction in the time-independent Schrödinger equation:
-ℏ²/(2m) (d²/dx²)[A exp(iB)] + V(x) A exp(iB) = E A exp(iB)
where m is the mass of the particle, V(x) is the potential energy function, and E is the total energy of the particle.
Simplifying this equation, we get:
-A exp(iB) ℏ²/(2m) [(d²/dx²) + 2imB(dx/dx) - B²] + V(x) A exp(iB) = E A exp(iB)
Dividing both sides by A exp(iB) and simplifying further, we get:
-ℏ²/(2m) (d²/dx²) + V(x) = E
Since the potential energy function V(x) is not specified in the problem, we cannot find the allowed energies and angular momenta. However, we can solve for the energy E in terms of the given variables:
E = -ℏ²/(2m) (d²/dx²) + V(x)
We can also express the allowed energies in terms of the quantum number n, which represents the energy level of the particle:
E_n = -ℏ²/(2m) (π²n²/a²) + V(x)
where a is a constant that represents the size of the system.
The allowed angular momenta can be expressed as:
L = ℏ√(l(l+1))
where l is the orbital angular momentum quantum number. The maximum value of l for a given energy level n is n-1, so the total angular momentum quantum number can be expressed as:
J = l + s
where s is the spin quantum number.
Thus, we can solve for the energy in terms of the quantum number n:
E = - \((ℏ^2\pi ^2n^2)/(2ma^2)\)
For more details regarding quantum number, visit:
https://brainly.com/question/16746749
#SPJ4
25 POINTS! URGENT! HELP PLS!! 3 PARTS BUT YOU CAN DO HOW EVER MANY U WANT
What do you know about the number of edges and vertices for each figure?
How do you know?
a)
A prism has 12 faces.
b)
A pyramid has 7 faces.
c)
A Platonic solid has 12 faces.
Answers
Consider the function below. (If an answer does not exist, enter DNE.) f(x) = 1/2 x^4 - 4x^2 + 2 (a) Find the interval of increase. (Enter your answer using interval notation.) Find the interval of decrease. (Enter your answer using interval notation.) (b) Find the local minimum value(s). (Enter your answers as a comma-separated list.) Find the local maximum value(s). (Enter your answers as a comma-separated list.) (c) Find the inflection points. Find the interval where the graph is concave upward. (Enter your answer using interval notation.) Find the interval where the graph is concave downward. (Enter your answer using interval notation.)
Answers
the interval where the graph is concave upward is (2/√3, ∞) and the interval where the graph is concave downward is(∞-2/√3).
The given function is f(x) = 1/2 x^4 - 4x^2 + 2.(a) To find the interval of increase, we need to find the values of x for which the function is increasing.To find the interval of decrease, we need to find the values of x for which the function is decreasing.We know that if f'(x) > 0, then the function is increasing in that interval. Similarly, if f'(x) < 0, then the function is decreasing in that interval.f'(x) = 2x³ - 8x= 2x(x² - 4)= 2x(x - 2)(x + 2)Critical points occur where f'(x) = 0, or where the derivative does not exist.f'(x) = 0 when 2x(x - 2)(x + 2) = 02x = 0 (x - 2)(x + 2) = 0x = 0, ±2The critical points are x = 0, ±2. We can use these critical points to determine the intervals of increase and decrease of the function.Using the first derivative test, we find that:On the interval (-∞, -2), f'(x) < 0, so f(x) is decreasing.On the interval (-2, 0), f'(x) > 0, so f(x) is increasing.On the interval (0, 2), f'(x) < 0, so f(x) is decreasing.On the interval (2, ∞), f'(x) > 0, so f(x) is increasing.Therefore, the interval of increase is (−2, 0) U (2, ∞) and the interval of decrease is (−∞, −2) U (0, 2).(b) To find the local minimums and maximums, we need to find the critical points of the function and then determine whether they correspond to a local minimum or maximum.To do this, we need to use the second derivative test. If f''(x) > 0, then the function has a local minimum at that point. If f''(x) < 0, then the function has a local maximum at that point.f''(x) = 6x² - 8f''(0) = -8 < 0, so f(x) has a local maximum at x = 0.f''(-2) = 20 > 0, so f(x) has a local minimum at x = -2.f''(2) = 20 > 0, so f(x) has a local minimum at x = 2.Therefore, the local maximum is at x = 0, and the local minimums are at x = -2 and x = 2.(c) To find the inflection points, we need to find where the concavity of the function changes. This occurs where the second derivative is zero or undefined.f''(x) = 6x² - 8= 2(3x² - 4)We need to find where 3x² - 4 = 0.3x² = 4x = ±2/√3The inflection points are at x = -2/√3 and x = 2/√3.To find the intervals where the function is concave upward or downward, we need to determine the sign of the second derivative.f''(x) > 0, the function is concave upward.f''(x) < 0, the function is concave downward.f''(-2/√3) = 2(3(-2/√3)² - 4) < 0, so the function is concave downward on the interval (-∞, -2/√3).f''(2/√3) = 2(3(2/√3)² - 4) > 0, so the function is concave upward on the interval (2/√3, ∞).
To know more about this, derivative visit
https://brainly.com/question/29144258
#SPJ11
given that count is an integer and count = 0, the following for-loop is an infinite loop. for (int j = 0; j < 1000; ) count++;
Answers
The loop will keep executing infinitely, leading to an infinite loop.
What is for loop ?
For loop can be defined as, it run the given code in the given number of times , at first it intialises the value and than checks the condition and than increments or decrements the value.
Yes, the given for-loop is an infinite loop.
The loop condition j < 1000 is based on the variable j, which is initialized to 0, but j is never incremented or modified inside the loop. Therefore, the condition j < 1000 will always be true, and the loop will continue to execute indefinitely.
Although the variable count is being incremented inside the loop, it is not being used in the loop condition or in any other way that would cause the loop to terminate.
Hence, the loop will keep executing infinitely, leading to an infinite loop.
To lean more about For loop from given link.
https://brainly.com/question/30494342
#SPJ1
Keith buys an item for $629. He gives the cashier a $50 bill. How much money should Keith get back?
Answers
Answer:
None
Step-by-step explanation:
This doesn't really make sense, If the item is 629$ and Keith only gives 50$ Keith is the one who should pay.
Answer:
Keith should get $43.71
Step-by-step explanation:
The answer is 43.71 because 50 minus 6.29 equals 43.71
Work out the volume of the cuboid 4cm 10cm 15cm

Answers
Answer:
600 m³
Step-by-step explanation:
Attached Below
If it helps, mark as brainliest. : )

Find the 9th term of the geometric sequence 9, 27, 81, ...
Answers
Answer:
a(9) = 59049
Step-by-step explanation:
The general term of a geometric sequence is a(n) = a(1)*r^(n - 1), where r is the common ratio.
Here, each new element is found by multiplying the previous one by 3. Thus, r = 3, and the general geometric series for this particular series is
a(n) = 9*3^(n - 1)
The 9th term is a(9) = 9*3(9 - 1) = 9*3^8 = 59049
The value of x is 6, what is the value of y?
What is the scale factor? Explain your reasoning:¾=0.75

Answers

2+2 for educational purposes
Answers
Answer:
2+2 =4
Step-by-step explanation:
Answer:
4
Step-by-step explanation: