which direction does the gradient v point in the direction of maximum increase or maximum decrease in v
Answers
The negative of the gradient (-grad f(x)) points in the direction of the maximum decrease of f from x.
The gradient of a scalar-valued function is a vector that points in the direction of the maximum increase of the function.
In other words, if we consider a point in the domain of the function and take the gradient at that point, the direction of the gradient vector indicates the order in which the function increases the most from that point. Conversely, the negative gradient points in the direction of the maximum decrease of the function.
Specifically, let f be a scalar-valued function of n variables \((f: R^n - > R),\)and let x be a point in the domain of f. The gradient of f at x is defined as the vector:
\(grad f(x) = (∂f/∂x1, ∂f/∂x2, ..., ∂f/∂xn)\)
where ∂f/∂xi denotes the partial derivative of f with respect to xi evaluated at x, the direction of the gradient vector grad f(x) at x is the direction in which f increases the most from x, and the magnitude of the gradient vector is the rate of change of f at x in that direction.
The negative of the gradient (-grad f(x)) points in the direction of the maximum decrease of f from x.
Learn more about gradient functions at
brainly.com/question/30865649
#SPJ4
Related Questions
Dan Pawlik is paid a straight commission of $5.75 for each item he sells. Last month he sold 103 items. Find his estimated and exact commissions.
Answers
Answer:
\(Estimated\ Commission = \$618\)
\(Exact\ Commission = \$592.25\)
Step-by-step explanation:
Given
\(Commission = \$5.75\)
\(Items = 103\)
Required
Find the estimate and exact commission
Estimate Commission
First, we need to approximate the given commission
\(Commission = \$6\)
\(Estimated\ Commission = Commission * Items\)
\(Estimated\ Commission = \$6 * 103\)
\(Estimated\ Commission = \$618\)
Exact Commission
\(Exact\ Commission = Actual\ Commission * Items\)
\(Exact\ Commission = \$5.75 * 103\)
\(Exact\ Commission = \$592.25\)
Simplify the following expression. 10x + 6 + 2(x + 5)
Answers
Answer:
12x+10
Step-by-step explanation:
10x+2(x+5)
10x+2x+10
12x+10
Plz answer my questions
Answers
I neeeeed heeeelp please

Answers
Answer:
10b/y^2
Step-by-step explanation:
Hope this helps! :)
The credit remaining on a phone card (in dollars) is a linear function of the total calling time made with the card (in minutes). The remaining credit after 36 minutes of calls is
$24.24, and the remaining credit after 55 minutes of calls is $21.20. What is the remaining credit after 63 minutes of calls?
Answers
The remaining credit after 63 minutes of calls is $19.92.
What is the remaining credit after 63 minutes of calls?From the information illustrated, the remaining credit after 36 minutes of calls is $24.24, and the remaining credit after 55 minutes of calls is $21.20.
The rate will be:
= (24.24 - 21.20) / (55 - 36)
= 3.04 / 19
= 0.16
The remaining credit after 63 minutes of calls will be:
= $21.20 - ((63 - 55) × $0.16)
= $21.20 - $1.28
= $19.92
The credit is $19.92.
Learn more about equations on:
brainly.com/question/2972832
#SPJ1
-1/4 plus 3/5
Answer or else
Answers
The algebric expression -1/4 + 3/5 is equal to 7/20 when simplified.
To solve the expression -1/4 + 3/5, we need to find a common denominator for the fractions and then perform the addition.
The common denominator for 4 and 5 is 20. We can rewrite the fractions with this denominator:
-1/4 = -5/20
3/5 = 12/20
Now that the fractions have the same denominator, we can add them:
-5/20 + 12/20 = (-5 + 12)/20 = 7/20
Therefore, -1/4 + 3/5 is equal to 7/20.
To further simplify the fraction, we can check if there is a common factor between the numerator and denominator. In this case, 7 and 20 have no common factors other than 1, so the fraction is already in its simplest form.
Thus, the final answer is 7/20.
For more such question on algebric expression. visit :
https://brainly.com/question/4344214
#SPJ8
The animals at a safari park include camels,
kangaroos and meerkats.
There are 12 more kangaroos than there are
camels.
There are 3 times as many meerkats as there
are camels.
There are the same number of kangaroos as
there are meerkats.
How many camels are there at the safari park?
Answers
m = 3c
k = m
Equating the RHS of the first two equations gives
3c = c + 12
2c = 12
c = 6
There are 6 camels
During a huge snowstorm in the White Mountains last year, it
snowed 60.5 cm in one day. Use the facts to find how much
this is in meters.
X
3
Conversion facts for length
1000 millimeters (mm) - 1 meter (m)
100 centimeters (cm) - 1 meter (m)
10 decimeters (dm) 1 meter (m)
1 dekameter (dam) -10 meters (m)
1 hectometer (hm) 100 meters (m)
1 kilometer (km)
1000 meters (m)
Answers
By using the facts given, 60.5 cm is 0.605 m or 0.605 meters.
Given: Convert 60.5 cm to meters
And the facts are as follows:
1000 milli-meters (mm) - 1 meter (m)
100 centimeters (cm) - 1 meter (m)
10 decimeters (dm) - 1 meter (m)
1 deka-meter (dam) -10 meters (m)
1 hectometer (hm) - 100 meters (m)
1 kilometer (km) - 1000 meters (m)
What is the length?
Length is the measurement of something from one point to another point.
Length can also be the distance between two points.
The shortest length between two times is known as displacement.
There are different ways to measure the length between two points or objects.
The SI unit of length is metered (m)
Also, kilometers or miles are used to measure large distances.
How to convert from centimeters (cm) to meters (m)?
1 meter or 1 m is equivalent to 100 centimeters or 100 cm. So let us apply the unitary method.
100 cm = 1 m
So 1 cm = 1 / 100 m
Therefore, x cm will be x / 100 m
Let’s solve the problem.
Given 60.5 cm to show in meters
So 100 cm = 1 m
1 cm = 1 / 100 m
60.5 cm = 60.5 / 100 m
60.5 cm = 0.605 m
Hence by using the facts given 60.5 cm is 0.605 m or 0.605 meters.
Know more about “length conversions” here: https://brainly.com/question/17930331
#SPJ9
HELP NEED ASAP PLS HELP

Answers
Answer:
MN = 56
Step-by-step explanation:
This can only be solved if we know the relation of MN to other dimensions of the trapezoid. If we assume MN is a midline (AM=MD, BN=NC), then MN is the average of the base lengths:
MN = (AB +CD)/2
2MN = AB +CD . . . . . multiply by 2
2(12x -4) = 8x +72 . . . fill in the given values for the segment lengths
24x -8 = 8x +72 . . . . . eliminate parentheses
16x = 80 . . . . . . . . . . . add 8-8x
x = 5 . . . . . . . . . . . . . . divide by 16
MN = 12(5) -4 = 56 . . . find the length of MN using its formula
Unsure of how to solve not getting answer in the choice list myself
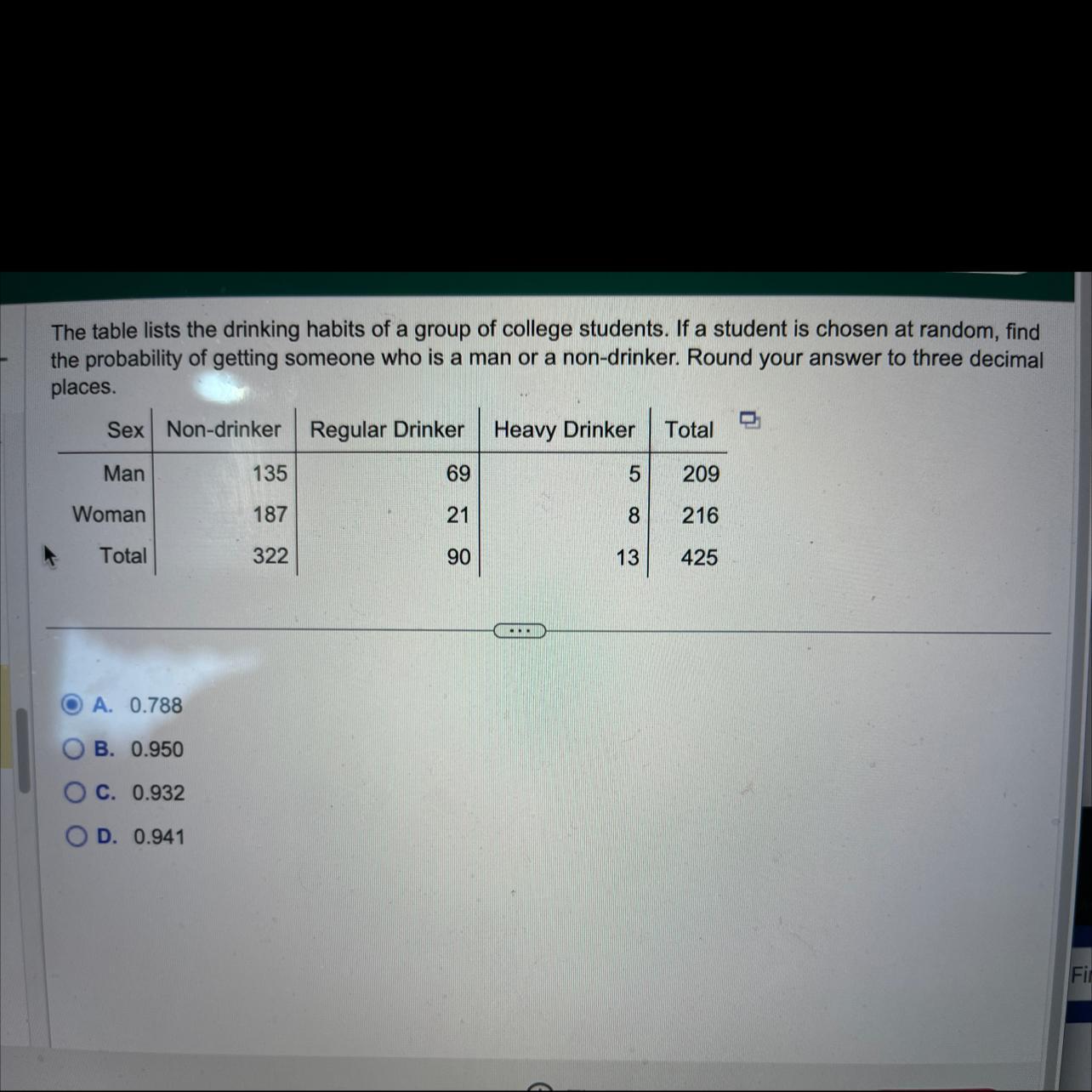
Answers
Option C is correct. probability of choosing man and non drinker is given s 0.932
What is probability?Probability is a branch of mathematics that deals with the study of random events or experiments, and the likelihood or chance of certain outcomes occurring. It is concerned with quantifying the uncertainty of events and helps us make predictions or informed decisions in situations where the outcome is not certain.
probability of choosing man and non drinker= 209 / 425 + 322 / 425 - 135 / 425
= 0.4917 +0.7576 - 0.3176
= 0.9317
this is approximately 0.932
Read more on probability here https://brainly.com/question/24756209
#SPJ1
among all simple closed curves in the plane oriented counterclockwise find the one alon which the work done
Answers
Using the Green's Theorem, the one along which the work done by the force is 11π/16.
In the given question we have to find the one along which the work done by the force is the greatest.
The given closed curves in the plane is
\(F(x,y)=\left(\frac{x^{2}y}{4} + \frac{y^3}{3}\right)\hat{i}+x\hat{j}\)
Suppose C be a simple smooth closed curve in the plane. It is also oriented counterclockwise.
Let S be the interior of C.
Let P = \(\frac{x^{2}y}{4} + \frac{y^3}{3}\) and Q = x
So the partial differentiation is
\(\frac{\partial P}{\partial y}=\frac{x^2}{4}+y^2\) and \(\frac{\partial Q}{\partial x}\) = 1
By the Green's Theorem, work done by F is given as
W= \(\oint \vec{F}d\vec{r}\)
W= \(\iint_{S}\left ( \frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y} \right )dxdy\)
W= \(\iint_{S}\left ( 1-\frac{x^2}{y}-y^2 \right )dxdy\)
Let C = x^2+y^2 = 1 and
x = rcosθ, y = rsinθ
0≤r≤1; 0≤θ≤2π
There;
W = \(\int_{r=0}^{1}\int_{\theta=0}^{2\pi}\left ( 1-\frac{r^2\cos^2\theta}{4}-r^2\sin^2\theta \right )\left|\frac{\partial(x,y)}{\partial{r,\theta}}\right|d\theta dr\)
and \(\frac{\partial (x,y)}{\partial(r, \theta)}=\left|\begin{matrix}\cos\theta &-r\sin\theta \\ \sin\theta & r\cos\theta\end{matrix} \right |\) = r
Thus;
W = \(\int_{r=0}^{1}\int_{\theta=0}^{2\pi}\left ( 1-\frac{r^2\cos^2\theta}{4}-r^2\sin^2\theta \right )rd\theta dr\)
After solving
W = 11π/16
Hence, the one along which the work done by the force is 11π/16.
To learn more about Green's Theorem link is here
brainly.com/question/28384298
#SPJ4
The right question is:
Among all simple smooth closed curves in the plane, oriented counterclockwise, find the one along which the work done by the force:
\(F(x,y)=\left(\frac{x^{2}y}{4} + \frac{y^3}{3}\right)\hat{i}+x\hat{j}\)
is the greatest. (Hint: First, use Green’s theorem to obtain an area integral—you will get partial credit if you only manage to complete this step.)
Find the quotient of z₁ by z2. Express your answer in
trigonometric
form.
² - 3 (0 (4) + (*))
Z₁ cos
+/sin
Z₂
²2 = 7 (cos(377)+
COS
8
O A. 7 (cos (577) + i sin (5/77))
8
B.
21(cos(577)+isin (577))
8
OC. 21 cos
21(cos(-7)+ i sin(-77))
O D. 7 (cos(-7) + + sin(-7))
i
+/sin
37T
8

Answers
The quotient of z₁ by z₂ in trigonometric form is:
7/21 * (cos(584°) + i sin(584°))
To find the quotient of z₁ by z₂ in trigonometric form, we'll express both complex numbers in trigonometric form and then divide them.
Let's represent z₁ in trigonometric form as z₁ = r₁(cosθ₁ + isinθ₁), where r₁ is the magnitude of z₁ and θ₁ is the argument of z₁.
We have:
z₁ = 7(cos(577°) + i sin(577°))
Now, let's represent z₂ in trigonometric form as z₂ = r₂(cosθ₂ + isinθ₂), where r₂ is the magnitude of z₂ and θ₂ is the argument of z₂.
From the given information, we have:
z₂ = 21(cos(-7°) + i sin(-77°))
To find the quotient, we divide z₁ by z₂:
z₁ / z₂ = (r₁/r₂) * [cos(θ₁ - θ₂) + i sin(θ₁ - θ₂)]
Substituting the given values, we have:
z₁ / z₂ = (7/21) * [cos(577° - (-7°)) + i sin(577° - (-7°))]
= (7/21) * [cos(584°) + i sin(584°)]
The quotient of z₁ by z₂ in trigonometric form is:
7/21 * (cos(584°) + i sin(584°))
Option C, 21(cos(-7°) + i sin(-77°)), is not the correct answer as it does not represent the quotient of z₁ by z₂.
For more questions on trigonometric form
https://brainly.com/question/31744474
#SPJ8
Caleb is going to invest 120 and leave it in an account for 18 years. Assuming the interest is compounded quarterly, what interest rate, to the nearest tenth of a percent would be required for Cale’s to end up with 300
Answers
The compound interest model has a quarterly interest rate is approximately 1.3 %.
How to determine the compound interest rate associated to an account
Herein we find the case of an amount of money deposited that is increased by means of compound interest, whose model is described below:
C' = C · (1 + r / 100)ⁿ
Where:
C - Original capital, in monetary units.C' - Resulting capital, in monetary units.r - Quarterly interest rate, in percentage.n - Number of quarters.First, clear the interest rate in compound interest model:
C' = C · (1 + r / 100)ⁿ
C' / C = (1 + r / 100)ⁿ
\(r = 100\cdot \left(\sqrt [n] {\frac {C'} {C}} - 1\right)\)
Second, substitute all known variables and make all calculations: (n = 72, C = 120, C' = 300)
\(n = 100 \cdot \left(\sqrt[72]{\frac{300}{120} } - 1\right)\)
n ≈ 1.281
The quarterly interst rate for the compound interest model is approximately 1.3 %.
To learn more on compound interest models: https://brainly.com/question/29335425
#SPJ1
Answer:5.1%
Step-by-step explanation:
Find the inverse of the function f(x) = 2x - 4.
g(x) = 1/2x - 1/4
g(x) = 1/4x - 1/2
g(x) = 4x + 2
g(x) = 3x+2
Answers
Answer:
None of the options are correct, but I got g(x)=1/2x+2.
Step-by-step explanation:
You start with the equation. You first need to change f(x) to y, and switch the x and y values. After this, your equation would be x=2y-4. Then, you need to icolate the y value, and to do that you first cancel out the four by adding it to both sides, and now your equation should be x+4=2y. The second step in icolating the y value is dividing everything in the equation by two. Now that the y is icolated, you equation should be y=1/2x+2. You then change the y to be g(x), and that's how I got my answer, g(x)=1/2x+2. You should ask your teacher about this, becuase from my calculations, none of the given responses would be correct. Sorry if that doesn't help you at all but yeah
Answer:
D, g(x) = 1/2 x + 2
Step-by-step explanation:
The second answer IS ONE TO ONE
Aunt Rebecca is pricing cakes for a baby shower she is throwing. She wants one large cake shaped like a duckling and also some cupcakes in pastel colors. Winchester Bakery charges $4 for each cupcake, plus $30 for the large cake. Linda's Sweet Shoppe charges $40 for the large cake and $2 for each cupcake. If Aunt Rebecca orders a certain number of cupcakes, the cost will be the same at either bakery. What would the total cost be?
Answers
Answer:
Yes
Step-by-step explanation
13/12=1 1/12
Bandhan Bank employee salary after 10 years
Answers
Answer:
- Banking Operations salary in India with less than 1 year of experience to 10 years ranges from ₹ 1.4 Lakhs to ₹ 7 Lakhs with an average annual salary of ₹ 3.1 Lakhs based on 261 latest salaries
Find two square numbers that total 45
Answers
x^2+^2=45
if ×=3 and y=6
then 9+36=45
If the mean of a normal distribution is 26, what is the median of the distribution? O A. 22 O B. 14 C. 26 D. 18 SUB

Answers
Answer:
B
Step-by-step explanation:
26 divides by 2 = 13
13+2=14
If the mean GPA among students is 3.25 with a standard deviation of 0.75, what is the probability that a random sample of 300 students will have a mean GPA greater than 3.30
Answers
Answer:
The value is \(P(X > 3.30) = 0.12405\)
Step-by-step explanation:
From the question we are told that
The mean GPA is \(\mu = 3.25\)
The standard deviation is \(\sigma = 0.75\)
The sample size is n = 300
Generally the standard error of mean is mathematically represented as
\(\sigma_{\= x} = \frac{\sigma }{\sqrt{n} }\)
=> \(\sigma_{\= x} = \frac{0.75}{\sqrt{300} }\)
=> \(\sigma_{\= x} = 0.0433\)
Generally the probability that a random sample of 300 students will have a mean GPA greater than 3.30 is mathematically represented as
\(P(X > 3.30) = P(\frac{X - \mu}{\sigma_{\= x}} > \frac{3.30 -3.25}{ 0.0433} )\)
\(\frac{\= X -\mu}{\sigma } = Z (The \ standardized \ value\ of \ \= X )\)
\(P(X > 3.30) = P(Z> 1.155 )\)
From the z table the probability of (Z > 1.155 ) is
\(P(Z> 1.155 ) = 0.12405\)
\(P(X > 3.30) = 0.12405\)
HELPPPPPPPPPP !!!!!!!!!!

Answers
Answer:
Step-by-step explanation:
0.0000015
Sketch the lines through the point with the indicated slopes. Make the sketches on the same set of coordinate axes
Point
Slopes
(1, 1)
(a) 3 (b) -3 (c) -5/2 (d) Undefined
Answers
The sketch for slope is attached below.
What is slope?A line's slope is determined by how its y coordinate changes in relation to how its x coordinate changes. y and x are the net changes in the y and x coordinates, respectively. Therefore, it is possible to write the change in y coordinate with respect to the change in x coordinate as,
m = Δy/Δx where, m is the slope
Given:
Point Slopes
(1, 1) (a) 3
_ (b) -3
_ (c) -5/2
_ (d) Undefined
a) Now, using slope intercept form
y - 1= 3 (x-1)
y- 1= 3x- 3
y= 3x - 2
(b) Equation of a line has a slope -3 is given by
y - 1= (-3) (x-1)
y-1 = 3- 3x
y = -3x + 4
(c) Equation of a line has a slope -5/2 is given by
y - 1= (-5/2) (x-1)
y-1 = -5/2x + 5/2
y= -5/2x + 7/2
(d) The line parallel to y axis and passes through given point : x=1
"undefined" means the line is vertical.
Learn more about slope here:
https://brainly.com/question/10945523
#SPJ1

Is (1,8) a solution to the system of equations 3x+y=9 2x+9y=20
Answers

how do i know which one?

Answers
The inequality value that would be able to show/x/ ≤ 5 is option A
What is inequality?
In mathematics, inequality refers to a mathematical statement that expresses a relationship between two quantities, indicating that one quantity is greater than, less than, or not equal to the other.
The symbol that we have is telling us that the value of the x would be less than or it would be seen to be equal to five.
We can see that /x/ ≤ 5 would exclude the negative values and this can be seen in the option that is marked option A
Learn more about inequality:https://brainly.com/question/20383699
#SPJ1
Compare the values of the following numbers, using the symbols > (greater than), < (less than), and = (equal to).
0.5 _____0.500
Answers
Answer:
0.5 = 0.500
Step-by-step explanation:
Both numbers are five-tenths. The zeros to the right of the 5 are not place holders and do not change the value of the number.
0.5 = 0.500
Diane purchased a computer that was originally sold for 1252.00 it was discounted 32% how much did she pay
Answers
Answer:
400.64 is your answer
Step-by-step explanation:
I need brainlyest PLZ!!!!
Whats 9+10?
Answer the question.
Answers
Answer: 21
Step-by-step explanation: Okay but actually its 19 :)
Simplify
(2x– 3) (5x4 – 7x3 + 6x2 – 9)
A. 10x5 – 29x4 + 33x3 - 18x2 18x + 27
B. 10x5 - x4-9x3 – 18x2 -18x - 27
C. 10x5 + 29x4 – 33x3 + 18x2 + 18x - 27
D. 10x5 + x4 + 33x3 + 18x2 + 18x + 27
Answers
Answer: (A)=10x5−29x4+33x3−18x2−18x+27
Step-by-step explanation:
How i solved it was by simplifying each answer there was available and (A) was the most compatiable answer!
=(2x+−3)(5x4+−7x3+6x2+−9)
=(2x)(5x4)+(2x)(−7x3)+(2x)(6x2)+(2x)(−9)+(−3)(5x4)+(−3)(−7x3)+(−3)(6x2)+(−3)(−9)
=10x5−14x4+12x3−18x−15x4+21x3−18x2+27
=10x5−29x4+33x3−18x2−18x+27
Answer:
=(2x+−3)(5x4+−7x3+6x2+−9)
=(2x)(5x4)+(2x)(−7x3)+(2x)(6x2)+(2x)(−9)+(−3)(5x4)+(−3)(−7x3)+(−3)(6x2)+(−3)(−9)
=10x5−14x4+12x3−18x−15x4+21x3−18x2+27
=10x5−29x4+33x3−18x2−18x+27
Step-by-step explanation:
This figure is the pre-image of a prism that has undergone a dilation with a scale factor of 2/5.
What is the surface area of the image after the dilation?
206225 m²
26845 m²
51512 m²
58225 m²
Answers
Answer:
Step-by-step explanation:

Answer:
Yeah. The answer is \(206\frac{2}{25}\).
Step-by-step explanation:
1) Convert 2-7i to trigonometric form
2) Use the n-th roots theorem to find the requested roots of the given complex number.
Find the cube roots of 125
Answers
Answer:
1) \(\sqrt{53}(\cos286^\circ+i\sin286^\circ)\)
2) \(\displaystyle 5,-\frac{5}{2}+\frac{5\sqrt{3}}{2}i,-\frac{5}{2}-\frac{5\sqrt{3}}{2}i\)
Step-by-step explanation:
Problem 1
\(z=2-7i\\\\r=\sqrt{a^2+b^2}=\sqrt{2^2+(-7)^2}=\sqrt{4+49}=\sqrt{53}\\\\\theta=\tan^{-1}(\frac{y}{x})=\tan^{-1}(\frac{-7}{2})\approx-74^\circ=360^\circ-74^\circ=286^\circ\\\\z=r\,(\cos\theta+i\sin\theta)=\sqrt{53}(\cos286^\circ+i\sin 286^\circ)\)
Problem 2
\(\displaystyle z^\frac{1}{n}=r^\frac{1}{n}\biggr[\text{cis}\biggr(\frac{\theta+2k\pi}{n}\biggr)\biggr]\,\,\,\,\,\,\,k=0,1,2,3,\,...\,,n-1\\\\z^\frac{1}{3}=125^\frac{1}{3}\biggr[\text{cis}\biggr(\frac{0+2(2)\pi}{3}\biggr)\biggr]=5\,\text{cis}\biggr(\frac{4\pi}{3}\biggr)=5\biggr(-\frac{1}{2}-\frac{\sqrt{3}}{2}i\biggr)=-\frac{5}{2}-\frac{5\sqrt{3}}{2}i\)
\(\displaystyle z^\frac{1}{3}=125^\frac{1}{3}\biggr[\text{cis}\biggr(\frac{0+2(1)\pi}{3}\biggr)\biggr]=5\,\text{cis}\biggr(\frac{2\pi}{3}\biggr)=5\biggr(-\frac{1}{2}+\frac{\sqrt{3}}{2}i\biggr)=-\frac{5}{2}+\frac{5\sqrt{3}}{2}i\)
\(\displaystyle z^\frac{1}{3}=125^\frac{1}{3}\biggr[\text{cis}\biggr(\frac{0+2(0)\pi}{3}\biggr)\biggr]=5\,\text{cis}(0)=5(1+0i)=5\)
Note that \(\text{cis}\,\theta=\cos\theta+i\sin\theta\) and \(125=125(\cos0^\circ+i\sin0^\circ)\)
At an airport, 79% of recent flights have arrived on time. A sample of 7flights is studied. a.Compute the mean of this probability distribution. Round to two decimal places, if needed.b.Compute the standard deviation of this probability distribution. Round to two decimal places, if needed.c.Find the probability that exactly4of the flights were on time. Round to three decimal places.d.Find the probability that lessthan 4of the flights were on time. Round to three decimal places.e.Find the probability that more than 5of the flights were on time. Round to three decimal places. f.Find the probability that at least5of the flights were on time. Round to three decimal places.g.Find the probability that no more than 5of the flights were on time. Round to three decimal places
Answers
Answer:
a. 5.53
b. 1.078
c. 0.126
d. 0.109
e. 0.549
f. 0.834
g. 0.451
Step-by-step explanation:
The percentage of the flights that arrive on time, P(x) = 79%
The number of flights in the sample, n = 7 flights
a. The mean of the probability distribution, μ = ∑x·P(x)
Therefore, we have; μₓ = n·p
μₓ = 7 × 79/100 = 5.53
b. The standard deviation, σₓ = √(n·p·(1 - p))
∴ σₓ = √(7 × 0.79 × (1 - 0.79)) ≈ 1.078
c. We have;
p = 0.79
q = 1 - p = 1 - 0.79 = 0.21
By binomial probability distribution formula, we have;
The probability of exactly four, P(Exactly 4) = ₇C₄·p⁴·q³
P(Exactly 4) = 35 × 0.79⁴×0.21³ ≈ 0.12625
d. The probability of less than 4 is given as follows;
P(Less than 4) = ₇C₀·p⁰·q⁷ + ₇C₁·p¹·q⁶ + ₇C₂·p²·q⁵ + ₇C₃·p³·q⁴
∴ P(Less than 4) = 1×0.79^0 * 0.21^7 + 7 * 0.79^1 × 0.21^6 + 21*0.79^2*0.29^5+ 85×0.79^3*0.21^4 ≈ 0.109
The probability of less than 4 is ≈ 0.109
e. The probability that more than 5 is given as follows;
P(More than 5) = ₇C₆·p⁶·q¹ + ₇C₇·p⁷·q⁰
7×0.79^6 * 0.21 + 1 * 0.79^7 × 0.21^0 ≈ 0.549
f. The probability that at least 5 of the flight were on time is given as follows;
P(At least 5) = ₇C₅·p⁵·q² + ₇C₆·p⁶·q¹ + ₇C₇·p⁷·q⁰
∴ P(At least 5) = 21×0.79^5 * 0.21^2 + 7×0.79^6 * 0.21 + 1 * 0.79^7 × 0.21^0 ≈ 0.834
g. For the probability that no more than 5 of the flights were on time, e have;
P(At most 5) = 1 - P(More than 5)
∴ P(At most 5) = 1 - 0.549 ≈ 0.451.