Answers
Does not pass 0,0
If I’m wrong so sorry
Related Questions
1. Pia wants to mail some fabric from New York to San Francisco. The box she uses to ship costs $4.35. To ship
it, it costs $25 for the first 10 kilograms and $3.89 for each additional kilogram. Pia's fabric weighs 22.3
kilograms.
a. Which of the following is the best estimate for how much it will cost to ship?
A $48
B. $61
C. $73
D$77
b. What will be the exact cost?
Answers
Answer:
73
Step-by-step explanation:
22.3-10=12.3
12.3*3.89=47.847
25+47.847=72
73 is the closest
in a right triangle cos0=4/5. what is the exact value of cot(0)
Answers
In a right triangle with cos0 = 4/5, the exact value of cot(0) is 4/3.
In a right triangle, if cos0 = 4/5, then the exact value of cot(0) can be found using the Pythagorean Theorem and the definition of cotangent.
First, let's use the Pythagorean Theorem to find the third side of the right triangle.
If cos0 = 4/5, then the adjacent side is 4 and the hypotenuse is 5. The Pythagorean Theorem states that a^2 + b^2 = c^2, where a and b are the legs of the right triangle and c is the hypotenuse. Plugging in the known values, we get:
4² + b² = 5²
16 + b² = 25
b² = 9
b = 3
Now that we know the third side of the right triangle, we can use the definition of cotangent to find the exact value of cot(0).
Cotangent is defined as the ratio of the adjacent side to the opposite side. In this case, the adjacent side is 4 and the opposite side is 3, so:
cot(0) = 4/3
Therefore, the exact value of cot(0) is 4/3.
Learn more about Cotangent here: brainly.com/question/21626237
#SPJ11
what is 28.5 inches in height?
Answers
help help help!! pleaseee

Answers
Answer:
b
Step-by-step explanation:
i dont know how to explain it lol but its b
with the options Givin I found the anserw was B
a 15-foot statue casts a 20-foot shadow. how tall is a person who casts a 4-foot-long shadow? question 19 options: a) 5 feet b) 0.33 feet c) 3.75 feet d) 3 feet
Answers
Answer:
d
Step-by-step explanation:
the ratio of height : shadow of statue is 15 : 20 = 3 : 4
the ratio of height : shadow of person will also be 3 : 4
jet height of person be h , then
\(\frac{h}{4}\) = \(\frac{3}{4}\) ( cross- multiply )
4h = 12 ( divide both sides by 4 )
h = 3
then the person is 3 feet tall
Answer:
d) 3 feet
Step-by-step explanation:
Let (N(t))t a Poisson process with rate 3 per min. Let Sn denote
the time of the n-th event.
Find a. E[S10]
b. E[S4|N(1) = 3]
c.Var(S10).
d. E[N(4) − N(2)|N(1) = 3].
e. P[T20 > 3].
Answers
For a Poisson process with rate λ, the interarrival times between events are exponentially distributed with parameter μ = 1/λ. So, the time between the (n-1)-th and n-th event, denoted as Tn, follows an exponential distribution with parameter μ = 1/3 minutes.
Since Sn is the sum of the first n interarrival times, we have:
Sn = T1 + T2 + ... + Tn
The sum of n exponential random variables with parameter μ is a gamma random variable with shape parameter n and scale parameter μ. Therefore, Sn follows a gamma distribution with shape parameter n and scale parameter μ.
In this case, n = 10 and μ = 1/3. So, E[S10] can be calculated as:
E[S10] = n * μ = 10 * (1/3)
= 10/3 minutes.
Therefore, E[S10] = 10/3 minutes.
b. E[S4|N(1) = 3]:
Given that N(1) = 3, we know that there are 3 events in the first minute. Therefore, the time of the 4th event, S4, will be the sum of the first 3 interarrival times plus the time between the 3rd and 4th event.
Using the same reasoning as in part a, we know that the sum of the first 3 interarrival times follows a gamma distribution with shape parameter 3 and scale parameter 1/3. The time between the 3rd and 4th event, denoted as T4, follows an exponential distribution with parameter 1/3.
So, S4 = T1 + T2 + T3 + T4.
Since T1, T2, T3 are independent of T4, we can calculate E[S4|N(1) = 3] as:
E[S4|N(1) = 3] = E[T1 + T2 + T3 + T4]
= E[T1 + T2 + T3] + E[T4]
= (3/3) + (1/3)
= 4/3 minutes.
Therefore, E[S4|N(1) = 3] = 4/3 minutes.
c. Var(S10):
The variance of Sn, Var(Sn), for a Poisson process with rate λ, is given by:
Var(Sn) = n * σ^2,
where σ^2 is the variance of the interarrival times.
In this case, n = 10 and the interarrival times are exponentially distributed with parameter μ = 1/3. The variance of an exponential distribution is \(\mu^2\)So, \(\sigma^2 = \left(\frac{1}{3}\right)^2\)
= 1/9.
Substituting the values into the formula, we have:
Var(S10) = 10 * (1/9)
= 10/9.
Therefore, Var(S10) = 10/9.
d. E[N(4) − N(2)|N(1) = 3]:
Given that N(1) = 3, we know that there are 3 events in the first minute. Therefore, at time t = 2 minutes, there will be 3 - 1 = 2 events that have already occurred.
Now, we need to find the expected value of the difference in the number of events between time t = 4 minutes and t = 2 minutes, given that there were 3 events at t = 1 minute.
Since the number of events in a Poisson process follows a Poisson distribution with rate λt, where t is
To know more about Poisson process visit:
https://brainly.com/question/31769241
#SPJ11
Determine the degree of the following sequence: -17, 19, 55, 91, 127, 163,...1 st degree4 th degree3 rd degree2 nd degree
Answers
-17 19 55 91 127 163
36 36 36 36 36
6^2 6^2 6^2 6^2 6^2
It's a second degree sequence
What is the arc length of a circle that has a 6-inch radius and a central angle that is 65
degrees? Use 3.14 for л and round your answer to the nearest hundredth.
Answers
The arc length of the circle with a 6-inch radius and a central angle of 65 degrees is approximately 6.81 inches.
To find the arc length of a circle with a radius of 6 inches and a central angle of 65 degrees, we can use the formula:
Arc Length \(= (\theta /360) \times (2 \times \pi \times r)\)
where θ is the central angle in degrees,
r is the radius of the circle,
and π is the mathematical constant (approximately 3.14).
Substituting the given values into the formula:
Arc Length \(= (65/360) \times (2 \times 3.14 \times 6)\)
Simplifying the equation:
Arc Length \(= (0.1806) \times (37.68)\)
Arc Length ≈ 6.805 inches.
Rounding the answer to the nearest hundredth, we have:
Arc Length ≈ 6.81 inches
For similar question on arc length.
https://brainly.com/question/31549226
#SPJ11
40 points
hey whats the answer
pls show step explanation
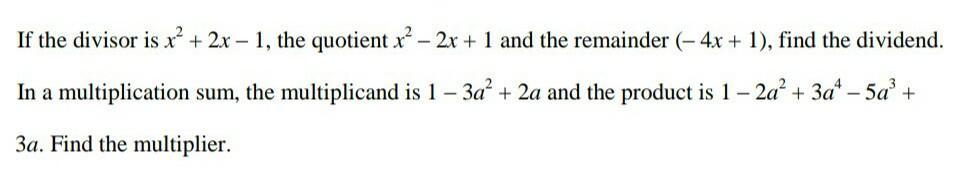
Answers
Answer:.
Answer:1.we have dividend =divisor*quotient+remainder=
(x²+2x-1)(x²-2x+1)+(-4x+1)
=x²(x²-2x+1)+2x(x²-2x+1)-1(x²-2x+1)-4x+1
=x⁴-2x³+x²+2x³-4x²+2x-x²+2x-1-4x+1
=x⁴-4x²
Dividend is x⁴-4x².
2.
Multiplier is a-a²+1.

Answer:
\(i \: hope \: the \: above \: picture \\ helps\)
\(have \: a \: nice \: day \: \)
\(#Liliflim\)

Let x be a positive number such that \(2x^2 = 4x + 9\). If x can be written in simplified form as \($\dfrac{a + \sqrt{b}}{c}$\) such that a, b, and c are positive integers, what is a + b + c?
Answers
Answer:
(4 ± 2\(\sqrt{22} \)) ÷ 4
Step-by-step explanation:
i changed equation to be 2x² - 4x - 9 = 0
i used the quadratic formula: (-b ± \(\sqrt{b^2-4ac} \)) ÷ 2a
where:
a = 2
b = -4
c = -9
Which exressionsl is equivalent to (q6)2
Answers
Answer:
q^12
Step-by-step explanation:
(q^6)^2
using the power of power rule we can multiply the exponents
q^6^2 = q^ (6*2) = q^ 12
I don't know what to do with this one????!!!!!

Answers
Answer:
Step-by-step explanation:
height of post ÷ length of shadow = 2/10 = ⅕
height of tower is ⅕ the length of its shadow.
⅕×125 = 25
The tower is 25 feet tall
Answer correctly please !!!!!!!!!!!!!!! Will mark brainliest !!!!!!!!!!!!!!!!!!!

Answers
Answer:
x=70
Step-by-step explanation:
If we extend the lines we can create an imaginary angle that is directly vertically opposite angle x (see picture for visualisation).
Then, using the rule that alternate interior angles are equal, we can deduct that this new angle is 30+40=70 degrees.
Finally, we know that vertically opposite angles are also equal meaning that x=70 degrees.
Hope this helped!

Place the LETTER of each value in its location in the real number system below

Answers
Answer:
Rational numbers are; A, E, F, I
Integers are; H and D
Whole numbers are J and B
Natural numbers is G
Please find attached the location of the letters on the real number system
Step-by-step explanation:
Rational numbers are numbers that can be expressed as the ratio, a/b, of two numbers as a/b where a and b are integers
Integers are the negative and positive whole numbers
Whole numbers are the positive counting numbers from 0 and above
Natural numbers are the positive counting numbers, sometimes including 0.

At the beginning of an experiment, the
number of bacteria in a colony was counted
at time t= 0. The number of bacteria in
the colony t minutes after the initial count
is modeled by the function below.
192
165
120
What is the average rate of change in the
number of bacteria for minutes 1 through 3
of the experiment?
9
45
A. 36
B. 48
C. 72
D. 96
--
Answers
Answer:
b
Step-by-step explanation:
i think it b! your welcome
Explanation:
Help with slope pleaseee
^^

Answers
You have to do to get the answer
(25 POINTS!!!!) a rectangular garden measures 5 feet by 4 feet. The length and width are both increased by the same amount and the new area is 56 square feet. What are the new dimensions of the garden?
Answers
The new dimensions of the garden are 8 feet and 7 feet.
What is rectangle?A rectangle is a part of a quadrilateral, whose sides are parallel to each other and equal.
Given that,
The length of rectangular garden = 5 feet,
And the width of rectangular garden = 4 feet.
The area of rectangular garden = 5 x 4 = 10 square feet.
Let the length and width are increased by x feet, to make the new area 56 square feet.
The new length = 5 + x,
and new width = 4 + x.
The area = 56
(5 + x) × (4 + x) = 56
Substitute, x= 3 which satisfies the equation,
So, the new length of garden = 5 + 3 = 8 feet,
And the new width of garden = 4 + 3 = 7 feet.
To know more about Rectangle on:
https://brainly.com/question/15019502
#SPJ5
question:
$1.59 for 12 shells
Answers
Answer:
about $0.13
Step-by-step explanation:
Answer:
13 cents
Step-by-step explanation:
1.59 divided by 12
Deshaun is selling raffle tickets for every 4 tickets he charge $28
Answers
Answer:
28/4=7
Step-by-step explanation:
Divide 4 by 28 and you get 7
Verify that the inverse of A™ is (A-')?. Hint: Use the multiplication rule for tranposes, (CD)? = DCT.
Answers
The inverse of the transpose of matrix A is equal to the transpose of the inverse of matrix A.
To verify that the inverse of A transpose (A^T) is equal to the transpose of the inverse of A (A^-1), we can use the multiplication rule for transposes, which states that (CD)^T = D^T * C^T.
Let's assume that A is an invertible matrix. We want to show that (A^T)^-1 = (A^-1)^T.
First, let's take the inverse of A^T:
(A^T)^-1 * A^T = I,
where I is the identity matrix.
Now, let's take the transpose of both sides:
(A^T)^T * (A^T)^-1 = I^T.
Simplifying the equation:
A^-1 * (A^T)^T = I.
Since the transpose of a transpose is the original matrix, we have:
A^-1 * A^T = I.
Now, let's take the transpose of both sides:
(A^-1 * A^T)^T = I^T.
Using the multiplication rule for transposes, we have:
(A^T)^T * (A^-1)^T = I.
Again, since the transpose of a transpose is the original matrix, we get:
A * (A^-1)^T = I.
Now, let's take the transpose of both sides:
(A * (A^-1)^T)^T = I^T.
Using the multiplication rule for transposes, we have:
((A^-1)^T)^T * A^T = I.
Simplifying further, we get:
A^-1 * A^T = I.
Comparing this with the earlier equation, we see that they are identical. Therefore, we have verified that the inverse of A transpose (A^T) is equal to the transpose of the inverse of A (A^-1).
In conclusion, (A^T)^-1 = (A^-1)^T.
To know more about inverse,
https://brainly.com/question/13593989
#SPJ11
"Use the graphical method to solve this problem:
Minimize Z = 15 X_1 + 20 X_2
Subject to X_1 + 2 X_2 ≥ 10
2X_1 – 3X_2 ≤ 6
X_1 + X_2 ≥ 6
and X_1 ≥ 0, X_2 ≥ 0"
Answers
Answer:
(X_1, X_2) = (2, 4)
Z = 110
Step-by-step explanation:
You want a graphical solution to ...
minimize Z = 15 X_1 +20 X_2
subject to ...
X_1 + 2 X_2 ≥ 102X_1 – 3X_2 ≤ 6X_1 + X_2 ≥ 6X_1 ≥ 0 X_2 ≥ 0GraphA graph of the reverse of the inequalities is attached. This makes the feasible solution region be white (rather than shaded multiple times), so its vertices are easier to see. (The dashed lines are part of the solution space.)
The vertex of the solution space that minimized the objective function is (X_1, X_2) = (2, 4). The minimum value of Z is 110.

two widely used metrics of variation are the __________ and the _________.
Answers
The two widely used metrics of variation are the coefficient of variation (CV) and the standard deviation (SD).
Coefficient of variation (CV) is a measure of relative variation and is often used to compare variation between populations or groups with different means. It is calculated as the ratio of the standard deviation to the mean, multiplied by 100 to express the result as a percentage. It's a dimensionless value, which means it can be used to compare the variation of different variables that are measured in different units.
Standard deviation (SD) is a measure of the amount of variation or dispersion of a set of values. It is calculated as the square root of the variance, which is the average of the squared differences from the mean. Standard deviation is a measure of absolute variation and is typically used to describe the spread of data within a single population or group.
Both of these metrics are important in understanding the variation within a population, with the CV being useful in comparing different groups and SD being used to describe the spread of data within a single group.
Learn more about standard deviation here: https://brainly.com/question/475676
#SPJ4
the sequence log 12(162), log 12(x), log 12(y), log 12(z), log 12(1250) is an arithmetic progression. what is x?
Answers
For a sequence \(log_{12} (162), log_{12} (x), log_{12}(y) , log_{12}(z) , log_{12}(1250)\) of arithmetic progression, the value of x is 270.
Given sequence;
\(log_{12} (162), log_{12} (x), log_{12}(y) , log_{12}(z) , log_{12}(1250)\)
The given sequence is an arithmetic progression,
\(log_{12} (162)+4d = log_{12}(1250)\)
Here, d is a common difference;
\(4d = log_{12}(1250)-log_{12} (162)\)
\(= log_{12}(1250/162)\)
\(d =\frac{1}{4} [log_{12}(1250/162)]\)
\(d = log_{12}(1250/162)^1^/^4\)
As we know the value of d we now need to add it to the first term to find x;
⇒ \(log_{12}(162)+ log_{12}(1250/162)^1^/^4\)
x = \((162)(1250/162)^1^/^4\)
x = 270
Hence, the value of x is 270.
To learn more about arithmetic progression click here:
brainly.com/question/20385181
#SPJ4
can anyone solve this?
6÷2(1+2)=
Answers
Answer:
9
Solving steps:
=> 6÷2(1+2)
divide 6 by 2
=> 3(1+2)
add values inside the bracket
=> 3(3)
multiply 3 by 3
=> 9
Answer:
9
Step-by-step explanation:
Use parenthesis, exponents, multiplication, division, addition, and subtraction, witch stands for PEMDAS.
1. 1+2 is the first step, since it is in the parenthesis. This gives you 3
2. You do 6÷2, since that is the next step. Since the operations are from left to right , you move on the next step, witch is divison. This also gives you 3.
3. You do the final step, witch is to multiply, so you do 3 x 3 , witch gives you 9.
Jenny has finished 12 of the 20 lessons and her piano book what percent did she finish
Answers
Answer:
\(let \: the \: percentage \: be \: x \\ therfore \: x\%of \: 20 = 12 \\ \frac{x}{100} \times 20 = 12 \\ \frac{x}{5} = 12 \\ x = 12 \times 5 \\ x = 60\%\)
hope it will help you
Arithmetic and geometric sequences plato/edumentuM

Answers
Answer:
A
Step-by-step explanation:
tank 2 goes down by a constant difference : -40
a zoo sponsored a one-day contest to name a new baby elephant. zoo visitors deposited entries in a special box between noon and 8 p.m. . the number of entries in the box t hours after noon is modeled by a differentiable function e for . values of , in hundreds of entries, at various times t are shown in the table above. (a) use the data in the table to approximate the rate, in hundreds of entries per hour, at which entries were being deposited at time . show the computations that lead to your answer. (b) use a trapezoidal sum with four subintervals given by the table to approximate the value of . using correct units, explain the meaning of in terms of the number of entries. (c) at 8 p.m., volunteers began to process the entries. they processed the entries at a rate modeled by the function p, where hundred of entries per hour for . according to the model, how many entries had not yet been processed by midnight ? (d) according to the model from part (c), at what time were the entries being processed most quickly? justify your answer?
Answers
(a) At 4pm, the rate is (130-70)/(4-2) = 30 entries/hour. (b) The trapezoidal sum approximates E(8) = 700 entries. (c) According to the model, 600 entries had not been processed by midnight. (d) The entries were being processed most quickly at 8pm, when p(8) = 60 entries/hour.
(a) At 4pm, the rate is (130-70)/(4-2) = 30 entries/hour.
(b) The trapezoidal sum is
E(8) = (50 + 70 + 110 + 130)/4 = 700/4
= 175.
E(8)=700 entries.
(c) According to the model, p(8) = 60 entries/hour. Since 8pm to midnight is 4 hours, the number of entries that had not been processed by midnight is 60*4 = 240 entries.
(d) The entries were being processed most quickly at 8pm, when p(8) = 60 entries/hour At 4pm, the rate of entry deposits was approximated by calculating the change in the number of entries over the change in the time, which was (130-70)/(4-2) = 30 entries/hour. Using a trapezoidal sum with four subintervals given by the table, E(8) was approximated to be 700 entries. According to the model, p(8) = 60 entries/hour, so the number of entries that had not been processed by midnight was 60*4 = 240 entries. The entries were being processed most quickly at 8pm, when p(8) = 60 entries/hour.
Learn more about hours here
https://brainly.com/question/13533620
#SPJ4
Sophia tas $146.32 imfer savings account. She has -3212.19 in her checking account
Which one of the following inequalities correctly compares the account values
Choose 1 answer
146.22 < -212.19
-212.13 < 146.22
Which one of the following descriptions is comed
Choose 1 answer
Sophia's savings account has a lower account value than her checking account
Answers
Answer: 1. -212.13 < 146.22
2. Sofia‘s checking account has a lower account value in her savings account
Step-by-step explanation: Your welcome
Answer:
B
Step-by-step explanation:
:)
Please help me !!!!!!!!

Answers
Answer:
The Eastern Continental Trail is 5,376 miles and the Erie Canalway Trail is 384 miles
Step-by-step explanation:
I took 5,760 divided it by 15 and got 384, I then subtracted 5,760 by 384 and got 5,376
help me solve this.

Answers
Answer:
A' (-1,2), B' (-5,-3), C' (3,2)
Step-by-step explanation:
Reflect triangle ABC across the y-axis.
Ry-axis: (x,y) → (-x,y)
A (1,2) → A' (-1,2)
B (5,-3) → B' (-5,-3)
C (-3,2) → C' (3,2)
I hope this helps :)
Answer:
this the season to be jolly falalalalaaaa la la la la
