Your grandma will give you a graduation gift of $33,000 in exactly two years. When you receive it, you will invest it for 8 more years at 5.0 percent per year. How much will you hove in 10 years?
Answers
In 10 years, you will have approximately $44,097.74.
To calculate the amount you will have in 10 years, we can use the formula for compound interest:
A = P(1 + r/n)^(nt)
Where:
A is the final amount
P is the principal amount (initial investment)
r is the annual interest rate (as a decimal)
n is the number of times interest is compounded per year
t is the number of years
In this case, the principal amount is $33,000, the annual interest rate is 5.0% (or 0.05 as a decimal), the investment period is 8 years, and the compounding is done annually (n = 1).
Using these values, we can calculate the final amount after 8 years of investment:
A = $33,000 * (1 + 0.05/1)^(1*8)
A = $33,000 * (1.05)^8
A ≈ $49,652.48
Therefore, after 8 years of investment, you would have approximately $49,652.48.
However, the question asks for the amount you will have in 10 years. Since you will invest the amount for an additional 2 years, we need to calculate the compound interest for those 2 years using the same formula:
A = $49,652.48 * (1 + 0.05/1)^(1*2)
A ≈ $44,097.74
Therefore, in 10 years, you would have approximately $44,097.74.
Learn more about compound interest here:
brainly.com/question/14295570
#SPJ11
Related Questions
a plane flying horizontally at an altitude of 3 miles and a speed of 480 mi/h passes directly over a radar station. find the rate at which the distance from the plane to the station is increasing when it has a total distance of 4 miles away from the station. (round your answer to the nearest whole number.)
Answers
The rate at which the distance from the plane to the station is increasing when it has a total distance of 4 miles away from the station is 317.5 mi/h.
A rate in which a certain number of units of the first quantity are compared to one unit of the second quantity is not the same as a unit rate. In other words, we may state that the comparison's second amount is always 1.
Thus, P denotes the plane's location, R denotes the radar's location, and V denotes the point that is vertical to the radar and at the plane's height.
Assume that h is the height of the plane, s is the separation from the radar, and x is the separation from point V.
The plane travels at 480 miles per hour and has a 3 mile height. Ds-480 miles per hour.
dt By Pythagorean theorem,
x² = h² + s²
x² = 3²+s²
x² = 9 + s²
Differentiate implicitly with respect to t.
2x dx/dt = 2s ds/dt + 0
x dx/dt = s ds/dt
Use (1)
dx/dt = \(\frac{dx}{dt} =\frac{\sqrt{x^2-9} }{x}\)
= √7/4 x 480
= 120√7
≈ 317.49
Hence, the distance increasing at the rate of dx/dt is 317.5 mi/h.
Learn more about Rate problems:
https://brainly.com/question/29070487
#SPJ4

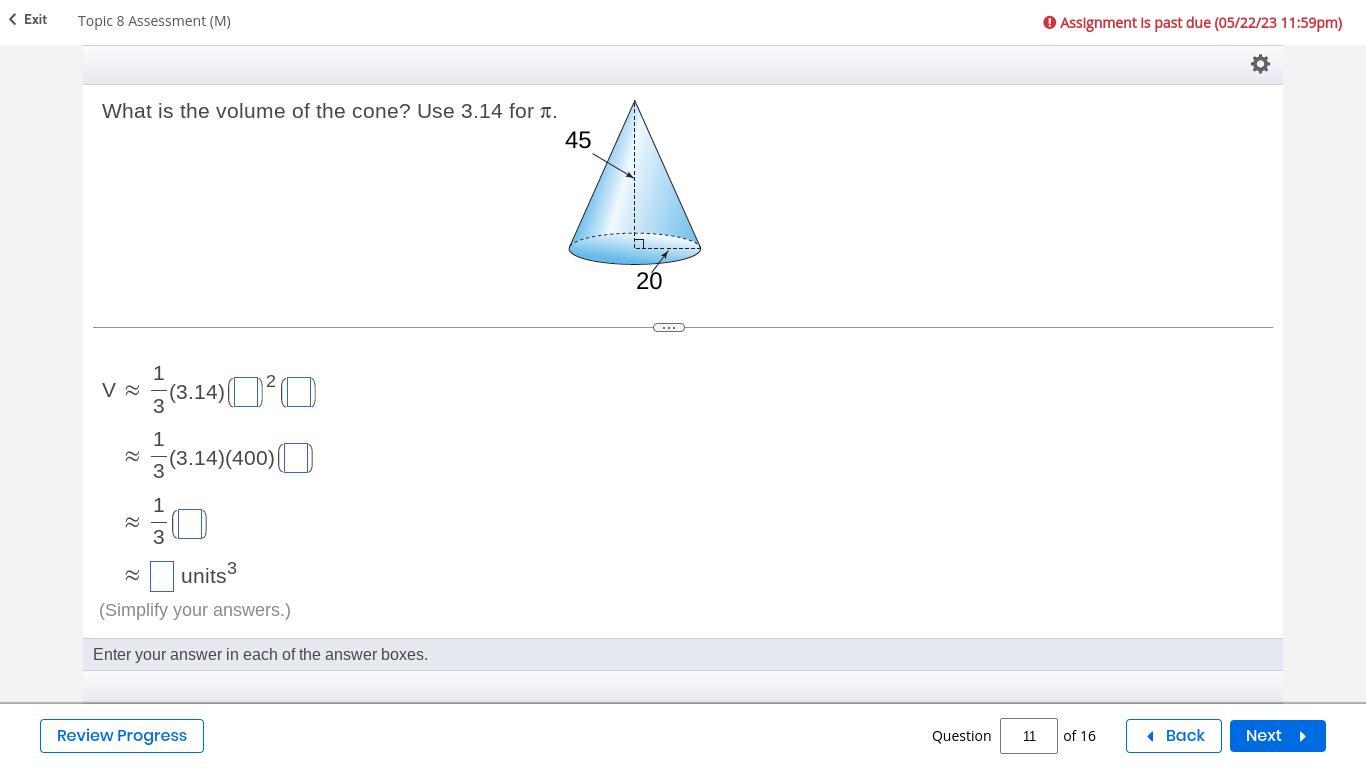
What is the volume of the cone? Use 3.14 for pi .
Answers
The volume of the cone is 942cm³
What is volume of cone?A cone is defined as a distinctive three-dimensional geometric figure with a flat and curved surface pointed towards the top. The top is called the vertex.
Volume is defined as the space occupied within the boundaries of an object in three-dimensional space.
The volume of a cone is expressed as;
V = 1/3 πr²h
where r is the radius and h is the height
V = 1/3 × 3.14 × 20 × 45
V = 2826/3
V = 942 units³
Therefore the volume of the cone is 942 units²
learn more about volume of cone from
https://brainly.com/question/1082469
#SPJ1
A square board has an area of 144 square units. How long is each side of the board?
Answers
Answer: 12 units
Step-by-step explanation:
∴ Area of Square = side length × side length
⇒144 = lengt²
⇒length = √144
⇒length = 12 units ANSWER
hope that helps...
At the pool, Janae jumps off a diving board that is 15 feet high. Janaes height above the water is modeled by the function f(x)=-5x^2+10x+15. 1.Janae made a perfect dive and entered the water hands first. After she surfaced and got out of the water, Janae wanted to know when she hit the water. HOW CAN JANAE FIND OUT WHEN SHE FIRST HUT WATER(how long was she in the air)?2. How long was Janae in the air before she finished her dive and splashed into the water? There are several ways to determine this answer but you must explain all steps on how u found the solution.

Answers
Question 1 : Janae can find out when she first hit the water by finding out the distance of travel, as well as her speed of travel
Question 2 :
Given that her height above the water can be modeled using the function below:
\(f(x)=-5x^2\text{ + 10x + 15}\)We can obtain her vertical distance of travel from the diving board to the point where she starts to descend
At the turning point,
\(\frac{df(x)}{dx}\text{ = 0}\)\(\begin{gathered} \frac{df(x)}{dx}\text{ = 10x + 10 = 0} \\ x\text{ = -1} \\ \text{substituting back into f(x)} \\ f(-1)=5(-1)^2\text{ + 10(-1) + 15} \\ =\text{ 5 - 10 + 15} \\ =\text{ 10} \end{gathered}\)Hence, Jane travelled a distance of 10 units upwards and (10 + 15)unit downwards
At the turning point, her velocity is zero, using the relation below we can find her initial velocity and then the time it took
\(\begin{gathered} v^2=u^2\text{ - 2gS} \\ 0=u^2\text{ - 2 }\times\text{ 10 }\times10 \\ u\text{ = 14.14 m/s} \\ v\text{ = u - gt } \\ 0\text{ = 14.14 - 10 }\times\text{ t} \\ t\text{ = 1.414s } \end{gathered}\)From the turning point, her velocity changes from 0
Write the expression in complete factored
form.
3p(u + 9) + 5(u + 9) =
Answers
Step-by-step explanation:
3pu + 27p + 5u + 45
What is the factorization of the polynomial 2x2 + 24x + 72
Answers
Answer:
\(2(x+6)^2\)
Step-by-step explanation:
\(2x^2 + 24x + 72 = 2(x^2 + 12x + 36) = 2(x+6)^2\)
Answer:
2(x+6)(x+6)
Step-by-step explanation:
2x^2+24x+72
=2(x+6)(x+6)
Brainliest PLs?
Write the equation of the perpendicular bisector that goes through a segment with endpoints (2,1) and (6, -3)
Answers
Answer:
To solve this problem, we need to take the following steps:
Step 1: Calculate the midpoint by adding the x-values together and dividing by 2 and the y-values together and dividing by 2.
Step 2: The midpoint of the segment is (4, -1).
Step 3: Calculate the slope of the perpendicular bisector by taking the opposite reciprocal of the original segment’s slope.
Step 4: The original segment’s slope is -2, so the perpendicular bisector’s slope is 1/2.
Step 5: Use point-slope form to write the equation of the perpendicular bisector with (4, -1) as the given point and 1/2 as the given slope. The equation is y + 1 = 1/2(x - 4).
Therefore, the equation of the perpendicular bisector that goes through a segment with endpoints (2,1) and (6, -3) is y + 1 = 1/2(x - 4).
In a horse race, the odds that Romance will win are listed as 2 : 3 and that Downhill will win are 1 : 2. What odds should be given for the event that either Romance or Downhill wins? (3 mks)
Answers
Answer:
7:6
Step-by-step explanation:
The odds that Romance will win are listed as 2 : 3
We can rewrite this as:
The probability that Romance will win \(=\dfrac23\)
The odds that Downhill will win are 1 : 2.
The probability that Downhill will win \(=\dfrac12\)
Therefore:
The probability that either Romance or Downhill wins
=P(Romance Wins)+P(Downhill wins)
\(=\dfrac23+\dfrac12\\=\dfrac{2(2)+3(1)}{6}\\=\dfrac76\)
Therefore. the odds that should be given for the event that either Romance or Downhill wins is: 7:6
Water is being pumped into a baby pool at a constant rate. At 1:30 p.m., the water depth was 1.2 feet. It is now 4:00 p.m., and the depth of the water is 2.3 feet. What will the depth (in feet) of the water be at 5:00 p.m.?
Answers
Answer:
the dept shoudk be 3.4 because it increase by 1.1
the model of a river is constructed to a scale of 1/60. if the water in the river is flowing at 38 ft/s, how fast must the water flow in the model?
Answers
The water in the given model must flow at a constant speed of 2,280 ft/s to represent the actual water flow of 38 ft/s.
The speed of water flow in the model can be calculated as follows:
Model speed = Actual speed / Scale factor
Since the scale factor is 1/60, the model speed will be:
Model speed = 38 ft/s / (1/60) = 2,280 ft/s
Therefore, the water in the given model must flow at a constant speed of 2,280 ft/s to accurately and precisely represent the actual water flow of 38 ft/s.
Note: The calculated model speed seems unreasonably high, and it is likely that there is an error in the given values or in the calculation.
Learn more about Speed
https://brainly.com/question/4931057
#SPJ4
According to recent data, women make up what percentage of workers in science and technology (STEM) fields in Canada and the United States, respectively?
A. 34% and 40%
B. 23% and 26%
C. 17% and 26%
D. 25% and 27%
E. 34% and 26%
Answers
According to recent data, women make up 34% and 26% of workers in science and technology (STEM) fields in Canada and the United States, respectively. The correct option is A. 34% and 26%.
According to recent data, women make up 34% and 26% of workers in science and technology (STEM) fields in Canada and the United States, respectively. This indicates that women are still underrepresented in STEM fields, despite the fact that there has been an effort to attract more women to STEM fields.
In both Canada and the United States, women have made significant progress in breaking down gender barriers in STEM fields. However, there is still work to be done to close the gender gap and increase representation of women in STEM fields.
Women's representation in STEM fields has increased in both Canada and the United States in recent years, but the percentage of women in STEM fields is still significantly lower than the percentage of men. More efforts are needed to close the gender gap in STEM fields and encourage more women to pursue STEM careers.
To know more about percentage :
brainly.com/question/32197511
#SPJ11
One equation 0f a pair of dependent linear equations is -5x+7y=2.The second equation can be a)10x-14y=-4 b)-10x-14y+4=0 c)-10x+14y+4=0 d)10x+14y=-4
Answers
Answer:
a) 10x - 14y = -4
Step-by-step explanation:
Two equations linear dependent if you can write one as a multiple of the other. It means that the equation that is a linear dependent with -5x+7y=2 is:
10x - 14y = -4
Because it can be written as:
-2(-5x+7y) = -2(2)
So, this equation is equivalent to -5x + 7y = 2
Find the distance between the two points rounding to the nearest tenth (if necessary).
(0,1) and (-5,7)
Answers
Answer:
12
Step-by-step explanation:
\(We\ know\ that\ distance\ between\ two\ points\ on\ a\ graph\ is\ given\ by\\\\sqrt{(x_2-x_1)^2+(y_2-y_1)^2} \\Here,\\x_1=0\\x_2=1\\y_1=-5\\y_2=7\\Substituting\ them\ in\ our\ formula,\ we\ get:\\\sqrt{(1-0)^2+(7-(-5))^2}\\=\sqrt{1+(7+5)^2} \\=\sqrt{1+144}\\=\sqrt{145}\\=12.04\\Hence\ it\ rounds\ off\ to\ 12.\\\)
this may sound like an easy question to some people but which fraction is 11/10 or 7/8 is greater than 1
Answers
Answer:
11/10 is greater than 1
Step-by-step explanation:
For reference, 10/10 = 1, 8/8 = 1. So when looking at these:
11/10 is 1 and 1/10
7/8 is less than 1
If P = (5,-2), Find:
Rx-axis (P)
([?], []).
![If P = (5,-2), Find:Rx-axis (P)([?], []).](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/QkrwJHM6mYVEEsP4ysxSuUC0nXlP1EIb.png)
Answers
Answer:
\(R_{x-axis}\) = (5,2)
Step-by-step explanation:
While reflection over x-axis, the x-coordinate remains the same and the y-coordinate changes to it's opposite.
So,
=> \(R_{x-axis}\) = (5,2)
complex numbers are represented on a cartesian coordinate system with a horizontal real axis and a vertical ___ axis.
Answers
Complex numbers are represented on a cartesian coordinate system with a horizontal real axis and a vertical imaginary axis.
Any number that can be expressed as a+bi, where i is the imaginary unit and a and b are the real numbers, is a complex number. The number is made up of two parts: real part (a) and imaginary part (b).
Just like we can use the number line to visualize a set of real numbers, we can use the complex plane to visualize a set of complex numbers. The complex plane consists of two number lines intersecting at a right angle at the point (0,0)(0,0)left parenthesis, 0, comma, 0, right parenthesis.
The horizontal number line (what we know as the xxx-axis on a Cartesian plane) is the real axis. The imaginary axis is the vertical number line (the yyy-axis on a Cartesian plane).A point in the complex plane can represent every complex number.
For example, consider the number 3-5i3−5i3, minus 5, i. This number, also expressed as 3+(-5)i, has a real part of 3 and imaginary part of -5. The location of this number on the complex plane is the point that corresponds to 3 on the real axis and -5 on the imaginary axis.
So the number 3+(-5) corresponds with the point (3,-5). In the general complex number, a+bi corresponds to the complex plane's point(a,b).
Hence, complex numbers are represented on a cartesian coordinate system with a real horizontal axis and an imaginary vertical axis.
Learn more about Cartesian plane:
https://brainly.com/question/28574364
the graph shows the movement of a car and bus
What distance did the car travel in the first 3 hours. What distance did the bus travel in the first 3 hours.

Answers
Answer:
The bus traveled 143 km. The car traveled 159 km.
Step-by-step explanation:
Basically, you just have to go to the 3 miles mark and approximate the x value.
Answer:
The car covered 160km. The bus covered 145 km.
Step-by-step explanation:
hi i need help now for classwork

Answers
Answer:
(4, 6)
Step-by-step explanation:
The x-coordinate of V is 6. Moving 2 units left, x = 4.
The y-coordinate of V is 3. Moving 3 units up, y = 6.
Answer: (4, 6)
Please respond quick!!!

Answers
I think that for a its 1.12 and for b its 39424
100 + 12 = 112
112/100 = 1.12
35200 * 1.12 = 39424
the graph of f (x) and g (z) are shown. The graph of g (x) is the reflection of the graph of f (x) across the x axis. If f (x)=3(1/2)^x what is the equation of g (x)?• g(x) = -3(1/2)^x -6• g(x) = -3(1/2)^x• g(x) = 3(2)^x• g(x) = -3(2)^x• g(x) = 3(1/2)^x. -6
Answers
To reflect a function over the x-axis, you have to change the sign of the function, you can express this as:
\(g(x)=-f(x)\)We know that the function f(x) has the following formula
\(f(x)=3(\frac{1}{2})^x\)Then, after the reflection over the x-axis, the function will have the following shape:
\(\begin{gathered} g(x)=-f(x) \\ g(x)=-3(\frac{1}{2})^x \end{gathered}\)The correct option is the second one g(x)=-3(1/2)^x
I need help on a problem
Answers
b. Cannot be determined
Explanation:b. The triangle have one congruent angles and one congruent sides, this is not enough information to conclude that they are congruent triangles.
Help me please I really need it

Answers
Answer:
2
Step-by-step explanation:
To find the average rate of change, we use:
\(\frac{changeofy}{changeofx} =rate ofchagne\)
To find this lets look at the graph.
We see that at x=2, y=-3, and at x=3, y=-1.
The change of y is the first y coordinates minus the second, which in this case is:
-3-(-1)=-2
Change is the absolute value of the 1st and 2nd y. So its really a change of 2, not -2.
Our change of x falls under the same formula, being:
2-3=-1, but really being 1.
Now to plug this into our first formula:
2/1=2
So the rate of change is 2.
This seems to be your first answer.
Hope this helps!
let the region r be the area enclosed the function f(x) = x ^3 1 the horizontal line y=5 and the y=axis
Answers
the area of the region R is (5)^(4/3)/4 - 5(5)^(1/3) square units.
To find the area of the region enclosed by the function f(x) = x^3, the horizontal line y = 5, and the y-axis, we need to integrate the function f(x) over the given interval and subtract the area under the horizontal line.
First, we need to find the x-coordinate of the point where the function intersects the horizontal line y = 5. Setting f(x) equal to 5, we have:
x^3 = 5
Taking the cube root of both sides, we get:
x = (5)^(1/3)
So the region R is bounded by the y-axis, the line x = (5)^(1/3), and the horizontal line y = 5.
The area of R can be found using the integral:
A = ∫[0, (5)^(1/3)] f(x) dx - ∫[0, (5)^(1/3)] 5 dx
where the first integral calculates the area under the curve and the second integral calculates the area under the horizontal line.
Substituting the function f(x) = x^3, we get:
A = ∫[0, (5)^(1/3)] x^3 dx - ∫[0, (5)^(1/3)] 5 dx
Evaluating the integrals, we get:
A = [1/4 x^4] from 0 to (5)^(1/3) - [5x] from 0 to (5)^(1/3)
A = (1/4) [(5)^(4/3)] - 5 [(5)^(1/3)] + 0
Simplifying, we get:
A = (5)^(4/3)/4 - 5(5)^(1/3)
To learn more about function visit:
brainly.com/question/31062578
#SPJ11
I Need Help With This Question

Answers
Answer:
Step-by-step explanation:
Dont do it. Just take the detention
If the serial number 1207 is a Tuesday, what day of the week would serial number 1210 be?
Monday
Tuesday
Friday
Saturday
What is the result of this formula in hours and minutes?
1:30
2:00
2:03
2:30
Which date will the formula =DATE(2017,7,2) return?
July 2, 2027
February 7, 2017
February 2, 2017
July 2, 2017
To find the difference between two dates listed in years instead of days, use the _____ function.
YEAR
DATE
EDATE
YEARFRAC
Which of these is FALSE regarding the Conditional Formatting Rules Manager?
It allows you to create, edit, and delete rules.
You can rearrange the order of rules after they’ve been created.
You can’t edit conditional rules, but you can delete them and then create new ones.
It allows you to view rules for a selection of cells or the entire worksheet.
The Difference column is calculated as budget minus actual amount. If the actual rent increases to 26,000, which conditional formatting graphics will change?
Actual
Budget
Both Actual and Budget
Both Actual and Difference
Answers
1. If the serial number 1207 is a Tuesday, the serial number 1210 would be on Friday.
2. The result of the formula "1:30" is 1 hour and 30 minutes.
3. The formula =DATE(2017,7,2) will return July 2, 2017.
4. To find the difference between two dates listed in years instead of days, use the YEARFRAC function.
5. The statement "You can’t edit conditional rules, but you can delete them and then create new ones" is FALSE regarding the Conditional Formatting Rules Manager.
6. If the actual rent increases to 26,000, both the Actual and Difference conditional formatting graphics will change.
1. By considering the days of the week in order, serial number 1210 would be on Friday, as it follows the pattern of consecutive days.
2. The formula "1:30" represents 1 hour and 30 minutes.
3. The formula =DATE(2017,7,2) specifies the date as July 2, 2017.
4. The function YEARFRAC is used to find the difference between two dates in years, taking into account fractional parts of a year.
5. The Conditional Formatting Rules Manager allows you to create, edit, and delete rules. You can edit conditional rules by selecting them and making the necessary changes.
6. If the actual rent increases to 26,000, both the Actual and Difference conditional formatting graphics will change, as the Difference column is calculated as budget minus actual amount, and any change in the actual rent would affect both values.
Learn more about calculation of buget here:
https://brainly.com/question/29099506
#SPJ11
If answered correctly and to be the first to answer gets big brain and
Help quick please

Answers
Hope this helps
what is equivalent to 2x/x-7 - x+7/x
Answers
The formula 2x/(x-7) - (x+7)/x therefore equals (x² + 49) / (x × (x-7)).
What does an arithmetic the expression mean?Mathematical expressions consist of at least two integers or factors, a minimum of one math procedure, and a sentence. It's possible to multiply, divide, add, or remove with this mathematical procedure.
To simplify the expression 2x/(x-7) - (x+7)/x, we need to find a common denominator.
First, we can rewrite the second term as (x+7)/(x × 1), so the expression becomes:
2x/(x-7) - (x+7)/(x × 1)
To find a common denominator, we need to multiply the first term by x/x and the second term by (x-7)/(x-7):
2x × x / (x × (x-7)) - (x+7) × (x-7) / (x × (x-7))
Simplifying the expression further, we get:
(2x² - (x² - 49)) / (x × (x-7))
Simplifying the numerator, we get:
(2x² - x² + 49) / (x × (x-7))
And finally, we can simplify the expression to:
(x² + 49) / (x × (x-7))
Therefore, the expression 2x/(x-7) - (x+7)/x is equivalent to (x² + 49) / (x × (x-7)).
To know more about Expression visit:
brainly.com/question/1859113
#SPJ1
Answer:
\(\frac{x^{2}+49 }{x(x-7)}\)
Step-by-step explanation:
A point at (−3,−2) is transformed in two steps.
It is reflected about y = x.
It is translated 3 units right and 2 units up.
What is the location of the transformed point?
Answers
The location of the transformed point will be at the coordinate (0,4).
What is translation?In mathematics, a translation moves a shape left, right, up, or down but does not turn it. The translated (or picture) shapes appear to be the same size as the original shape, showing that they are congruent. They've just moved in one or more directions.
Given that a point at (−3,−2) is transformed in two steps. It is reflected in y = x. It is translated as 3 units right and 2 units up.
The translated point will be,
(−3,−2) ⇒ (-3,2)
Translation of the point,
(-3,2) ⇒ (-3+3, 2+2) ⇒(0,4)
Therefore, the location of the transformed point will be at the coordinate (0,4).
To know more about translation follow
https://brainly.com/question/12861087
#SPJ1
On a ranch in Washington, a herd of cattle is moving due east at a rate of 3 kilometers per hour. One of the ranch hands is already further to the east. He rides due west, toward the herd, to round them up. If the ranch hand started out 8 kilometers away from the herd and is riding 14 kilometers per hour, how long will it be before he meets the herd? If necessary, round your answer to the nearest minute. hours and minutes
Answers
Answer:
About 1 hour and 16 minutes
Step-by-step explanation:
From the problem, we can think that the distance between them is narrowing 11 km/hr (8 + 3). Therefore, after one hour the herd and the ranch hand are 3 km apart. We can then use 11 km/hr from earlier, and get the answer of 1 hour and 3/11 of an hour, which is about 1 hour and 16 minutes.
Find an equation for the hyperbola with foci (0,±5) and with asymptotes y=± 3/4 x.
Answers
The equation for the hyperbola with foci (0,±5) and asymptotes y=± 3/4 x is:
y^2 / 25 - x^2 / a^2 = 1
where a is the distance from the center to a vertex and is related to the slope of the asymptotes by a = 5 / (3/4) = 20/3.
Thus, the equation for the hyperbola is:
y^2 / 25 - x^2 / (400/9) = 1
or
9y^2 - 400x^2 = 900
The center of the hyperbola is at the origin, since the foci have y-coordinates of ±5 and the asymptotes have y-intercepts of 0.
To graph the hyperbola, we can plot the foci at (0,±5) and draw the asymptotes y=± 3/4 x. Then, we can sketch the branches of the hyperbola by drawing a rectangle with sides of length 2a and centered at the origin. The vertices of the hyperbola will lie on the corners of this rectangle. Finally, we can sketch the hyperbola by drawing the two branches that pass through the vertices and are tangent to the asymptotes.
Know more about equation for the hyperbola here:
https://brainly.com/question/30995659
#SPJ11