A teacher assigns 10 questions for homework and wants to randomly pick 3 questions to be graded. Which one of the following procedures would practice a simple random sample?

Answer:

1, 4, 9, 16, 25, 36, 49, (....)

Answer:

\(\frac{-7}{10}\ or \ 0.7\)

Step-by-step explanation:

step 1.

\(\frac{1}{3} (\frac{-6}{4}-\frac{1}{2}(\frac{6}{5}))\)

step 2.

put it in a calculator

step 3

=\(\frac{-7}{10}\ or \ 0.7\)

Solution

we need to convert the following expression:

four less than half a number n

Then the best answer is:

The variance of  is approximately 1.6361 (rounded up to fourth decimal place).

To find the variance of , we need to first calculate its expected value or mean, E(). We can do this by using the formula:

E() = Σ xi pi

where xi is the number of courses and pi is the probability of taking xi courses.

E() = (1)(0.02) + (2)(0.01) + (3)(0.20) + (4)(0.17) + (5)(0.39) + (6)(0.20) + (7)(0.01) = 4.31

So the expected value of  is 4.31.

Next, we need to calculate the variance of . We can use the formula:

Var() = E[( - E())^2]

where E() is the expected value of , as calculated above.

Var() = (1-4.31)^2(0.02) + (2-4.31)^2(0.01) + (3-4.31)^2(0.20) + (4-4.31)^2(0.17) + (5-4.31)^2(0.39) + (6-4.31)^2(0.20) + (7-4.31)^2(0.01)

Var() = 1.6361

Therefore, the variance of  is approximately 1.6361 (rounded up to fourth decimal place).

Learn more about variance here:

https://brainly.com/question/32159408

#SPJ11

Answer:

2652 is the correct answer

The domain of f is [-5, ∞) because the vertex is the global minimum of a parabola that opens up.

The domain of any polynomial, including quadratics, is (–∞, ∞).

The domain of a parabola is always all real numbers (sometimes written (−∞,∞). The domain is all real numbers because every single number on the x− axis results in a valid output for the function (a quadratic).

When x=−b2a, y=c−b24a. Therefore the maximum or minimum value of the quadratic is c−b24a. Whether it is the maximum or minimum can be determined by examining the sign of a. If a is positive, then the range is y≥c−b24a

Hence, The range here is [-5, ∞), because the vertex is the global minimum of a parabola that opens up, and the global minimum is the lowest value.

To know more about domain and range , visit :

brainly.com/question/28135761

#SPJ1

Lines have a larger m value, that is, m > 1 have steeper slope and lines having an m value between 0 and 1, usually in the form of a fraction have a flatter slope .

Slope is the rate of change in the dependent variable with respect to the independent variable.

For an equation of line of the type - y= mx +c , the slope is given by the m value.

Now, if the value of m > 1 like m=1,2,3, ... , the lines have a steeper slope and have a steep nature.

Similarly, if the value of m < 1 i.e. 0 < m < 1 like m=1/2,2/3, ... fractional values,  the lines have a flatter slope and do not have a steep nature.

To learn more about slope of a line , visit link - brainly.com/question/16180119

#SPJ4

The angle x in the figure is:

x = 34.45°

Trigonometry deals with the relationship between the ratios of the sides of a right-angled triangle with its angles.

Consider triangle ABE:

AB² = AE² + BE²  (Pythagoras theorem)

Notice that AE = BE (This is indicated using the red mark). So we have:

AB² = AE² + AE²

Substitute:

4² = AE² + AE²

16 = 2AE²

AE² = 16/2

AE² = 8

AE = √8

AE = 2√2 in

Using trig. ratio:

sin x° = AE/AD (sine = opposite/hypotenuse)

sin x° = 2√2 / 5

sin x° = 0.5657

x = sin⁻¹(0.5657)

x = 34.45°

Learn more about Trigonometry on:

brainly.com/question/11967894

#SPJ1

To find the length of one side of Steve's hamster pen, we can use the formula for the perimeter of a square, which is P = 4s, where P is the perimeter and s is the length of one side. In this case, we know that the perimeter is 240 centimeters, so we can set up the equation 240 = 4s. To solve for s, we can divide both sides by 4, which gives us s = 60 centimeters. Therefore, the length of one side of Steve's hamster pen is 60 centimeters. This means that all four sides of the pen are equal in length, and the area of the pen would be 60 x 60 = 3600 square centimeters.
Hi! To find the length of one side of Steve's square hamster pen with a perimeter of 240 centimeters, you can follow these steps:

1. Understand that the perimeter of a square is the sum of all its sides. In a square, all sides are equal.
2. Since there are 4 sides in a square, you can divide the total perimeter by 4 to find the length of one side.
3. Perform the calculation: 240 cm / 4 = 60 cm.

So, the length of one side of Steve's hamster pen is 60 centimeters.

To know more about perimeter visit:

https://brainly.com/question/397857

#SPJ11

To know the number of data points, simply count the number of values in the data, these values are separated by a comma

Option A: 18, 91, 93, 55, 57, 18. is not correct (it has 6 data points)

Option B: 25, 26, 28, 91, 18, is not correct ( it has 5 data points)

Option C: 9, 12, 8,5, 12, 9, 7. is correct (it has 7 data points)

Option D: 7,5, 9, 11, 13, 4, 9, 18. is not correct ( it has 8 data points)

Option E: 95, 91, 87, 99, 95, 84, 77​. is correct (it has 7 data points)

Options C and E are correct

Answer:

i need a picture for this problem.

Step-by-step explanation:

Answer:

250°

Step-by-step explanation:

Got it right on edge

Answer:

p=17+6h

Step-by-step explanation:

Step-by-step explanation:

Only option B shows a proportional relationship (y = 3x).

Answer:

D

Step-by-step explanation:

Y=3x-1 is written as the slope-intercept form y=mx+b don't let the -1 confuse you.

Answer:

x=3

Step-by-step explanation:

(5x*2)+ ((x-3)2)=42

10x+2x-6=42

12x-6=42

    -6  -6

12x=36

x=3

Answer:

x=3

Step-by-step explanation:

(5x*2)+ ((x-3)2)=42

10x+2x-6=42

12x-6=42

   -6  -6

12x=36

x=3

Answer: answer is sharan

Step-by-step explanation:

Answer:

n=-6

Step-by-step explanation:

You would first multiply by 3 because you are trying to get n by itself?

then you will get the equation n-6=-12 then you will add six cause again you want n by itself and you get n=-6 because -12 plus 6 is -6

The option that is not a statistical question is D. how tall are the corn plants?

A statistical question is one that may be answered by gathering data and for which the data will vary. Questions answered with a single data point are not statistical questions since the data utilized to answer the question is not variable.

A statistical question is one that can be answered by gathering varying amounts of data. A statistical inquiry is one that yields varying responses and outcomes (data). It must be collected on more than one person and there must be room for the facts to vary.

Therefore, based on the information illustrated, the correct option is D. It was too general and not specific

Learn more about statistics on;

https://brainly.com/question/12150562

#SPJ1

The domain of a function is the set of numbers that can go into a given function.

The set of input values (x) for which a function generates an output value is known as the domain of the function (y).

we can write \(y = f(x).\)

domain is the full set of x-values that can be plugged into a function to produce a y-value.

The most effective approach to finding a domain will depend on the type of function.

The domain is expressed using an open bracket or parenthesis, the domain's two endpoints separated by a comma, and then a closed bracket or parenthesis.

To find domain of function we should know the property of that function like what the function can take inside it.

Like if we consider square root function \(\sqrt{x}\) so inside root negative numbers are not allowed so value of x should be positive means x>=0

So domain of square root function [0, ∞).

To know more about domain of function here

https://brainly.com/question/13113489

#SPJ4

If cosθ = 3/5 and θ is in quadrant IV, then sin(2θ) = -24/25.

If cosθ = 3/5 and θ is in quadrant IV, then sin(2θ) can be found using the double-angle formula for sine.

1: Identify the sine value for θ in quadrant IV. Since cosθ = 3/5 (adjacent/hypotenuse), we can use the Pythagorean theorem to find the opposite side: (5² - 3²) = 25 - 9 = 16. The opposite side length is 4, but since θ is in quadrant IV, sinθ is negative, so sinθ = -4/5.

2: Use the double-angle formula for sine: sin(2θ) = 2sinθcosθ.

3: Plug in the values of sinθ and cosθ into the formula: sin(2θ) = 2(-4/5)(3/5).

4: Calculate sin(2θ): sin(2θ) = (-8/5)(3/5) = -24/25.

You can learn more about Quadrant at: brainly.com/question/30979352

#SPJ11

Answer:

19/1

Step-by-step explanation:

(2x5)+1÷2x16+1

10+(1÷2)x16+1

10+(1/2x 16)+1

(10+8)+1

18+1

19=19/1

Hey there!

=> 2×5+1÷2×16+1

=> 10 + 1 ÷ 32 + 1

=> 11 ÷ 33

=> \( \frac{11}{33} \)

=> \( \frac{1}{3} \)

Range is R={n^2: n is natural number} U {n(n+1) : n is natural number}

The expression ⌈y⌉⋅⌊y⌋ represents the product of the ceiling and floor functions of y.

To find the range of all possible values of y, we need to consider the possible values of the ceiling and floor functions individually.

1. Ceiling function (⌈y⌉): This function rounds y up to the nearest integer. Since y is greater than 0, the ceiling of y will always be greater than or equal to y.

2. Floor function (⌊y⌋): This function rounds y down to the nearest integer. Again, since y is greater than 0, the floor of y will always be less than or equal to y.

Now, let's consider the product of the ceiling and floor functions, ⌈y⌉⋅⌊y⌋.

The product ⌈y⌉⋅⌊y⌋ will always be greater than or equal to 0 since y > 0 and this can take only integral values.

Therefore, the range of all possible values of y such that ⌈y⌉⋅⌊y⌋ is the set R={n^2: n is natural number} U {n(n+1): n is natural number}

Learn more about Floor Function: https://brainly.com/question/24306698

#SPJ11

Answer:

13.26 * 6 =79.56

Step-by-step explanation:

Y = c1 e^(3t) + c2 t e^(3t) + c3 e^(29t) + 1/6 x + 1/3296 e^(2x) (2043 sin(5x) - 3160 cos(5x)) + 1/48 e^(3x) (x^2 - 15x - 12) To use the superposition approach, we need to first find the general solution to the homogeneous equation:
y- 7y"+ 41y- 87y = 0
This can be done by assuming a solution of the form e^(rt) and solving for the characteristic equation:
r^3 - 7r^2 + 41r - 87 = 0
Using synthetic division or other methods, we can factor this to:
(r - 3)(r - 3)(r - 29) = 0
So the general solution to the homogeneous equation is:
y_h = c1 e^(3t) + c2 t e^(3t) + c3 e^(29t)

Next, we need to find particular solutions to each of the three non-homogeneous terms on the right-hand side of the equation:
1) x: We assume a particular solution of the form Ax + B. Substituting into the equation and solving for A and B, we get:
yp1 = 1/6 x
2) e^2x sin(5x): We assume a particular solution of the form (C sin(5x) + D cos(5x)) e^(2x). Substituting into the equation and solving for C and D, we get:
yp2 = 1/3296 e^(2x) (2043 sin(5x) - 3160 cos(5x))
3) (x^2 - 9) e^3x: We assume a particular solution of the form (Ex^2 + Fx + G) e^(3x). Substituting into the equation and solving for E, F, and G, we get:
yp3 = 1/48 e^(3x) (x^2 - 15x - 12)

Finally, we add up the homogeneous and particular solutions to get the final form of the particular solution:
Y = y_h + yp1 + yp2 + yp3
Y = c1 e^(3t) + c2 t e^(3t) + c3 e^(29t) + 1/6 x + 1/3296 e^(2x) (2043 sin(5x) - 3160 cos(5x)) + 1/48 e^(3x) (x^2 - 15x - 12)

learn more about homogeneous equations here: brainly.com/question/29870459

#SPJ11

Answer:B,C

Step-by-step explanation:

the other do is always numbers with t be oossblie because of the quadratic formula

Answer:

The center of circle is: (-7,4) and Radius is 7 units

or (-4,7) and Radius is 7 units

We have to compare the given equation of circle with standard equation of circle

Given equation is:

2nd pic

down below

Standard equation of circle is:

3rd pic

down below

Here

h and k are coordinates of center of circle

So,

comparing

1st pic

down below

Hence,

The center of circle is: (-7,4) and Radius is 7 units

Keywords: Circle, radius

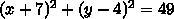
Answer:

Step-by-step explanation:

First expand the equation

That's

( x - 4)² + ( y - 7)² = 49

x² - 8x + 16 + y² - 14y + 49 - 49 = 0

x² + y² - 8x - 14y + 16 = 0

Comparing with the general equation of a circle

x² + y² + 2gx + 2fy + c = 0

2g = - 8 2f = - 14

g = - 4 f = - 7 c = 16

Center of a circle is ( - g , - f)

( --4 , --7)

Which is ( 4 , 7)

The radius of the circle is given by

r = √g² + f² - c

Where r is the radius

r = √ (-4)² + (-7)² - 16

= √16 + 49 - 16

= √49

Hope this helps you

Standard deviation of approximately 0.051 minutes for the quarter-mile runners. standard deviation for the one-mile runners is approximately 0.156 minutes.

To summarize the variability in the running times of quarter-mile and mile runners, we can calculate the sample standard deviation for each group of runners. This will provide a measure of the spread or dispersion of the data around the mean.

For the quarter-mile runners, the given times are 0.93, 0.97, 1.03, 0.90, and 1.00 minutes.

To compute the sample standard deviation, we first need to find the mean (average) of the quarter-mile times.

Adding up the times and dividing by the number of observations (5), we get a mean of 0.966 minutes.

Then, we calculate the deviations of each time from the mean, square these deviations, sum them up, divide by (n-1), where n is the number of observations, and take the square root.

This results in a sample standard deviation of approximately 0.051 minutes for the quarter-mile runners.

For the one-mile runners, the given times are 4.42, 4.45, 4.70, 4.80, and 4.60 minutes.

Following the same steps as above, we find that the sample standard deviation for the one-mile runners is approximately 0.156 minutes.

Therefore, based on the calculated sample standard deviations, the quarter-mile runners exhibit less variability or more consistent times compared to the one-mile runners.

To know more about Standard deviation visit:

brainly.com/question/13498201

#SPJ11

Explanation:

Angle E is 90 degrees. The segment DC = 53 is opposite this angle. Note how "DC" does not contain the letter "E". Furthermore, note how this is the largest side. So it's the hypotenuse.

The side ED = 28 is the opposite side of reference angle C, because "C" is nowhere to be found in the sequence "ED".

The side CE = 45 is the adjacent side because "E" is found in "CE".

The tangent ratio is...

tan(angle) = opposite/adjacent

tan(C) = ED/CE

tan(C) = 28/45