An identification code is to consist of 4 letters followed by 2 digits. Determine the following
a) How many different codes are possible if repetition of letters is permitted, repetition of numbers is not permitted, and the first three entries must all be the same letter
b) How many different codes are possible if the first letter must be an A, B, C, or D and repetition is not permitted?
Answers
explanation
Counting Possibilities with Repetition or No Repetition:
Counting the number of possibilities in a given situation can vary quite a bit depending on whether repetition is allowed or not. For example, if trying to find how many 6 letter passwords can be made with 10 letter choices, if the letters are allowed to be repeated then there are 10 choices for each letter in the password - resulting in... 10 x 10 x 10 x 10 x 10 x 10 = 10^6 =1,000,000 possible passwords.
However, if repetition of letters is not allowed, then there are 10 choices for the first letter, but only 9 for the second, 8 for the third, and so on. This results in only 10 x 9 x 8 x 7 x 6 x 5 = 151,200
Answer :
There are 26 letters to choose from and 10 digits (0 through 9).
(a) If the first three entries must all be the same letter, then there are 26 choices for the first entry, but only one choice for the second and third entries. The fourth entry can then be any letter, so there are 26 possible choices for the fourth entry. The fifth and sixth entry must be digits, but repetition of numbers are not permitted. So the fifth entry has 10 choices and the sixth entry only has 9 choices. This is a total of 26 x 1 x 1 x 26 x 10 x 9= 60,840
b) If the first letter must be one of A, B, C, or D, then there are 4 choices for the first entry. No repetition is allowed, so the second entry must be chosen out of the 25 remaining letters, and similarly the third and fourth entry will have 24 and 23 choices each. The fifth and sixth entry must be digits, but repetition of numbers are not permitted. So the fifth entry has 10 choices and the sixth entry only has 9 choices. 4 x 25 x 24 x 23 x 10 x 9=4,968,000 different codes
hope this helped alittle ..
Related Questions
Makayla is a botanist studying production of coconuts by two different groups of her coconut palms. She notices that Group 1 trees produce 25 percent more coconuts than Group 2. based on Makayla's observation, if Group 1 produced 150 coconuts, how many coconuts did group 2 produce?
Answers
If Group 1 trees produce 25 percent more coconuts than Group 2, proportionately, Group 2 trees produce 120 coconuts.
What is proportion?Proportion refers to the two ratios equated to each other.
Proportion shows how much quantity or value is contained in another.
We depict proportions using fractional values, such as fractions, decimals, and percentages.
The number of coconuts produced by Group 1 trees = 150
The percentage by which Group 1 trees produce more than Group 2 = 25%
Let Group 1's production compared to Group 2's = 1.25 (100% + 25%)
Let Group 2's production = 100% = 150/125 x 100
= 120 coconuts
Thus, Group 2 trees would produce 120 coconuts compared to Group 1 trees that produced 150, which was proportionately, 25% more.
Learn more about proportions at https://brainly.com/question/1496357
#SPJ1
E D 1389 xo С 76.2° B А Find the value of x. O 38.1 O 30.9 69 O 61.8

Answers
Based on the intersecting secants theorem, the value of x is: B. 30.9°
What is the Intersecting Secants Theorem?The intersecting secants theorem states that when two secants intersect, the measure of the angle they form is half the difference of the intercepted arcs.
Thus, based on the intersecting secants theorem, we would have the following:
x = 1/2(138 - 76.2)
x = 1/2(61.8)
x = 30.9°
Learn more about intersecting secants theorem on:
https://brainly.com/question/1626547
anybody answer me please with step by step explanation need complete detailed answer
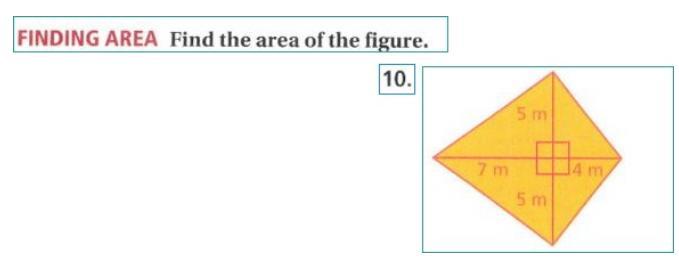
Answers
Answer:
A = 55
Step-by-step explanation:
take the two identical triangles and join them so that you get a rectangle wih sides 5 and 11. now multiply them togeter to get the are of the polynom
The area of triangle is 55 square centimeters.
What is area?Area is the amount of space occupied by a two-dimensional figure.
What is the formula for the area of triangle?The formula for the area of triangle is
\(Area = \frac{1}{2} \times base\times height\)
According to the given question.
We have a figure of a quadrilateral which is made up of four right angled tringles.
Now,
The area of a triangle with base 5cm and height 7 cm
= \(\frac{1}{2} \times 5\times 7\)
\(=\frac{35}{2}\)
\(= 17.5\) square centimeters
And, the area of triangle with base 4cm and height 5cm
= \(\frac{1}{2} \times 4\times 5\)
\(= 10\) square centimeters
Since, the quadrilateral is made up of 2 right angled triangle with base 5cm and height 7cm and 2 right angled triangle with base 4cm and height 5cm.
Therefore, the area of quadrilateral or the given fiure
= 2( area of triangle with height 7cm and base 5cm + area of triangle with base 4cm and height 5cm )
= 2(17.5 + 10) square centimeter
= 2 × 27.5
= 55 square centimeters
Hence, the area of triangle is 55 square centimeters.
Find out more information about area of triangle here:
https://brainly.com/question/19305981
#SPJ2
31 A packet of sweets has a mass of 0.24 kg. A grocer packed 12 such
packets of sweets into a box. If the total mass of the box and the sweets
is 4.06 kg, find the mass of the empty box.
Answers
Answer:
p = packet of sweets
12p = 4.06
p = .3383333
p = .340
The graph below shows the solutions to which inequality?
A. x^2-3x+3 ≥0
B. x² + 3x-3 <0
C. x²-3x+3<0
D. x² + 3x-3>0
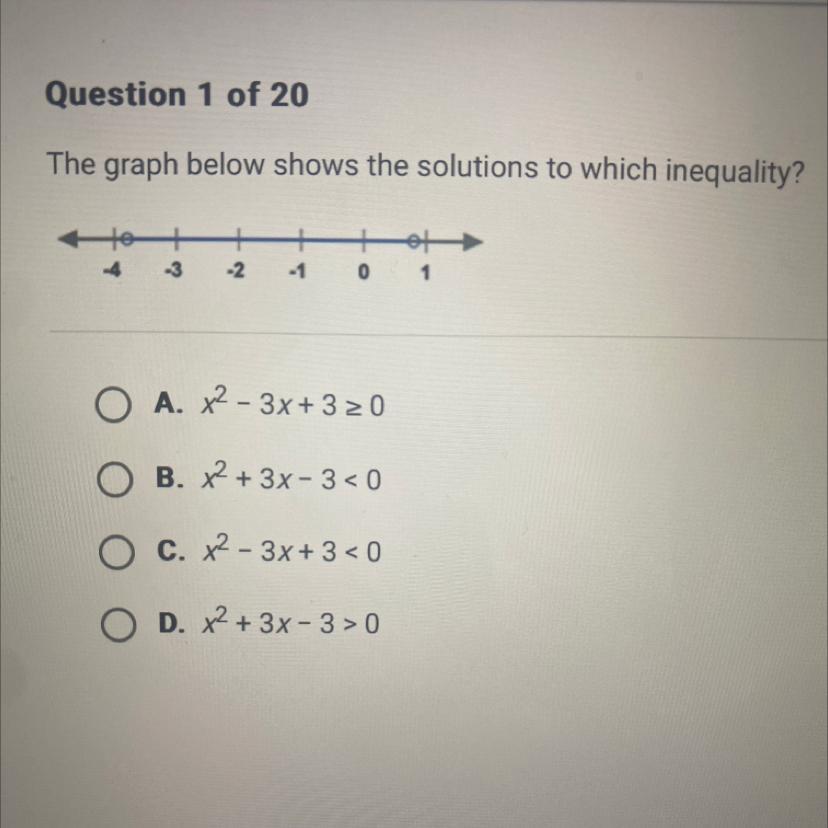
Answers
The inequality expression that corresponds to the solution of the inequality graph is x² + 3x - 3 < 0.
option B.
What is the solution of the inequality?The inequality expression that corresponds to the solution of the inequality graph is determined by simplifying the equations as follows;
The solution of the graph,
x > -4 and x < 1
The first equation with "≥" is ruled out because the graph doesn't have a thick dot.
Let's simplify the second expression;
x² + 3x - 3 < 0
solve using quadratic formula;
x > -3.79 or x < 0.79
The third expression is ruled out since its solution will be complex.
For the last expression;
x² + 3x - 3 > 0
x < -3.79 or x > 0.79
Thus, the correct inequality expression is x² + 3x - 3 < 0.
Learn more about inequality expression here: https://brainly.com/question/25275758
#SPJ1
5. A conical shaped pile of sand at the beach has a base circumference of 16.5 feet
and stands 10.4 feet high. The Department of Public Works is going to remove
75% of the sand. How much sand will be left in the pile after they remove 75% of
the sand?
Answers
Answer: 18.78 cubic feet
Step-by-step explanation:
The detailed analysis is attached below.

A ship is anchored off a long straight shoreline that runs north and south. From two observation points
miles apart on shore, the bearings of the ship are
and
. What is the distance from the ship to each of the observation points? Round each answer to the nearest tenth of a mile.
The distance from the north most ship to the observation is
miles.
The distance from the south most ship to the observation is
miles.
Answers
The distance from the north most ship to the observation is 2.9 miles and the distance from the south most ship to the observation is 9.9 miles.
The bearing is defined as the angle measured clockwise from the north direction. A ship is anchored off a long straight shoreline that runs north and south.
From two observation points miles apart on shore, the bearings of the ship are 52 degrees and 134 degrees respectively. To find the distance from the ship to each of the observation points, we can use trigonometry.
Let's call the distance from the north observation point to the ship x, and the distance from the south observation point to the ship y. The bearings from the north and south observation points can be drawn as follows:
[asy]
unitsize(1cm);
pair O = (0,0), N = (-2,0), S = (2,0), A = (-2,1), B = (2,-1);
draw(O--N--A,Arrow);
draw(O--S--B,Arrow);
\(label("$52^\circ$", N + 0.3*dir(52), NE);\)
\(label("$134^\circ$", S + 0.3*dir(134), SE);\)
draw(O--A--B--cycle,dashed);
\(label("$x$", (N+A)/2, W);\)
\(label("$y$", (S+B)/2, E);\)
[/asy]
We can use the tangent function to find x and y, since we have the angle and opposite side.
From the north observation point, we have:
\($$\tan(52^\circ) = \frac{x}{2}$$$$x = 2\tan(52^\circ) \approx 2.95$$\)
From the south observation point, we have:
\($$\tan(134^\circ) = \frac{y}{2}$$$$y = 2\tan(134^\circ) \approx 9.88$$\)
Therefore, the distance from the north most ship to the observation is 2.9 miles and the distance from the south most ship to the observation is 9.9 miles.
Know more about trigonometry here:
https://brainly.com/question/13729598
#SPJ8
A recipe for strawberry punch calls for 3/7 qt of ginger ale and 1/7 qt of strawberry soda. How much liquid is needed?
If the recipe is doubled, how much is needed?
If the recipe is halved, how much is needed?
Answers
Answer:4.7 qt of liquid is needed. If doubled, 8/7 qts of liquid is needed. if halved, 2/7 qts of liquid is needed.
Step-by-step explanation:
Add the two amounts of liquid to get the total amount of liquid:
1/7 qt + 3/7 qt = 4/7 qt (cannot be simplified further)
To double the recipe, multiply the total liquid amount by 2.
4/7 * 2/1 = 8/7
To half the recipe, multiply the total liquid amount by 1/2.
4/7 * 1/2 = 4/14 --> 2/7
The ratio of white marbles to blue marbles in Olivia's bag is 2 to 5. If there are more than 50 marbles in the bag, what is the minimum number of marbles that can be in the bag?
Answers
Step-by-step explanation:
the distributing ratio is 2:5.
that means for every 2 white marbles there must be 5 blue marbles.
so, we are taking about "groups" or multiples of 7 (2+5 = 7).
now, even 7×7 = 49 is too small.
but the next multiple of 7 (7×8 = 56) is now big enough to include at least 50 marbles.
so, in order to keep the 2:5 ratio strictly in place, the minimum number of marbles in the bag is 56.
C 67 zoom in 11 4 In math class, the following question was a warm-up for students. Write an equivalent expression for the following: 2 (3x + 4y +52) +4(x - y) to the warm-up question? 6.EE.4 · Alex wrote 24x + 4y + 147 Jonah wrote 9x + 4y + 72 Steven wrote 10x + 4y + 10Z Which, if any, of the three students wrote an expression that is equivalert to the warm-up question? Show you work to prove which expressio if any, are equivalent.
Answers
Answer:
Alex I think
Step-by-step explanation:
Given: AAEB and ADFC, ABCD, AE || DF, EB || FC, AC = DB
Prove: AEAB AFDC

Answers
By proving that ΔEAB and ΔFDC have congruent corresponding angles and proportional corresponding sides, we can conclude that ΔEAB ≅ ΔFDC.
Proving that Triangles are EqualGiven:
- Triangle ΔAEB and ΔDFC
- Line ABCD is straight (implies AC and BD are collinear)
- AE is parallel to DF
- EB is parallel to FC
- AC = DB
To prove: ΔEAB ≅ ΔFDC
Recall that:
AE || DF
EB || FC
AC = DB
AE || DF, EB || FC (Parallel lines with transversal line AB)
Corresponding angles are congruent:
∠AEB = ∠DFC (Corresponding angles)
∠EAB = ∠FDC (Corresponding angles)
Corresponding sides are proportional:
AE/DF = EB/FC (Corresponding sides)
AC/DB = BC/DC (Corresponding sides)
AC = DB
BC = DC (Equal ratios)
ΔEAB ≅ ΔFDC (By angle-side-angle (ASA) congruence)
∠EAB = ∠FDC
∠AEB = ∠DFC
AC = DB, BC = DC
Therefore, by proving that ΔEAB and ΔFDC have congruent corresponding angles and proportional corresponding sides, we can conclude that ΔEAB ≅ ΔFDC.
Learn more about triangles here:
https://brainly.com/question/30104125
#SPJ1
ASAPP PLEAASSEE!!!
Nathan deposits $940 every 2 months into his daughter's RESP. If the account earns 3.99% / annual, compound quarterly, how much will be in the account after 25 years?
Answers
There will be approximately $594,311.34 in Nathan's daughter's RESP after 25 years of depositing $940 every 2 months with a 3.99% annual interest rate compounded quarterly.
To calculate the amount in Nathan's daughter's RESP after 25 years, we can use the formula for compound interest:
A = P(1 + r/n)^(nt)
Where:
A = Final amount (amount in the account after 25 years)
P = Principal amount (amount deposited every 2 months)
r = Annual interest rate (in decimal form)
n = Number of times the interest is compounded per year
t = Number of years
In this case, Nathan deposits $940 every 2 months, so the principal amount (P) is $940. The annual interest rate (r) is 3.99% or 0.0399 in decimal form. Since the interest is compounded quarterly, the compounding frequency (n) is 4. The number of years (t) is 25.
Since Nathan deposits every 2 months, we need to calculate the total number of deposits made over 25 years. There are 12 months in a year, so in 25 years, there will be 25 * 12 = 300 months. However, since Nathan deposits every 2 months, the number of deposits (m) is 300 / 2 = 150.
Now, we can substitute these values into the formula:
A = 940(1 + 0.0399/4)^(4*25)
Calculating the exponent first:
(1 + 0.0399/4)^(4*25) ≈ 2.703236
Now, substituting the calculated exponent and the number of deposits into the formula:
A = 940 * 2.703236 * 150 ≈ $594,311.34
Therefore, there will be approximately $594,311.34 in Nathan's daughter's RESP after 25 years of depositing $940 every 2 months with a 3.99% annual interest rate compounded quarterly.
It's important to note that this calculation assumes Nathan makes the same $940 deposit every 2 months consistently over the 25-year period and does not make any withdrawals from the account during that time. Additionally, the actual amount may vary slightly due to rounding and any potential changes in interest rates over the years.
For more such questions on compounded visit:
https://brainly.com/question/24274034
#SPJ8
(12sin(pi/2x)*lnx)/((x³+5)(x-1))
lim as x approaches 1
Answers
The limit of the given function as x approaches 1 is 0.
To find the limit of the given function as x approaches 1, we need to evaluate the expression by substituting x = 1. Let's break it down step by step:
1. Begin by substituting x = 1 into the numerator:
\(\[12\sin\left(\frac{\pi}{2}\cdot 1\right)\ln(1) = 12\sin\left(\frac{\pi}{2}\right)\ln(1) = 12(1)\cdot 0 = 0\]\)
2. Now, substitute x = 1 into the denominator:
(1³ + 5)(1 - 1) = 6(0) = 0
3. Finally, divide the numerator by the denominator:
0/0
The result is an indeterminate form of 0/0, which means further analysis is required to determine the limit. To evaluate this limit, we can apply L'Hôpital's rule, which states that if we have an indeterminate form 0/0, we can take the derivative of the numerator and denominator and then evaluate the limit again. Applying L'Hôpital's rule:
4. Take the derivative of the numerator:
\(\[\frac{d}{dx}\left(12\sin\left(\frac{\pi}{2}x\right)\ln(x)\right) = 12\left(\cos\left(\frac{\pi}{2}x\right) \cdot \left(\frac{\pi}{2}\right) \cdot \frac{-1}{x} + \frac{\sin\left(\frac{\pi}{2}x\right)\ln(x)}{x}\right)\]\)
5. Take the derivative of the denominator:
\(\[\frac{d}{dx}\left((x^3 + 5)(x - 1)\right) = \frac{d}{dx}\left(x^4 - x^3 + 5x - 5\right) = 4x^3 - 3x^2 + 5\]\)
6. Substitute x = 1 into the derivatives:
Numerator: \(\[12\left(\cos\left(\frac{\pi}{2}\right) \cdot \left(\frac{\pi}{2}\right) \cdot \frac{-1}{1} + \sin\left(\frac{\pi}{2}\right) \cdot \frac{\ln(1)}{1}\right) = 0\]\)
Denominator: 4(1)³ - 3(1)² + 5 = 4 - 3 + 5 = 6
7. Now, reevaluate the limit using the derivatives:
lim as x approaches 1 of \(\[\frac{{12\left(\cos\left(\frac{\pi}{2}x\right) \cdot \left(\frac{\pi}{2}\right) \cdot \frac{{-1}}{{x}} + \sin\left(\frac{\pi}{2}x\right) \cdot \frac{{\ln(x)}}{{x}}\right)}}{{4x^3 - 3x^2 + 5}}\]\)
= 0 / 6
= 0
Therefore, the limit of the given function as x approaches 1 is 0.
For more such questions on L'Hôpital's rule
https://brainly.com/question/24116045
#SPJ8
What are the coordinates of the vertices of the final image? A. P’(12, -6), Q’(8, -7), R’(4, -4), and S‘(7, -1) B. P’(12, 8), Q’(8, 9), R’(4, 6), and S‘(7, 3) C. P’(-12, 6), Q’(-8, 7), R’(-4, 4), and S‘(-7, 1) D. P’(12, 6), Q’(8, 7), R’(4, 4), and S’(7, 1)
Answers
Answer:
Given that the vertices of quadrilateral PQRS are P(6,3), Q(4,2), R(2,4) and S(4,5) and the quadrilateral is dilated with a scale factor of 2, about the origin.
Now, let's find the new vertices of the dilated image:
Vertex P is dilated by a scale factor of 2, its new coordinates will be (2 × 6, 2 × 3) = (12, 6). Therefore, the new vertex P' is at (12, 6).
Vertex Q is dilated by a scale factor of 2, its new coordinates will be (2 × 4, 2 × 2) = (8, 4). Therefore, the new vertex Q' is at (8, 4).
Vertex R is dilated by a scale factor of 2, its new coordinates will be (2 × 2, 2 × 4) = (4, 8). Therefore, the new vertex R' is at (4, 8).
Vertex S is dilated by a scale factor of 2, its new coordinates will be (2 × 4, 2 × 5) = (8, 10). Therefore, the new vertex S' is at (8, 10).
Therefore, the coordinates of the vertices of the final image are P’(12, 6), Q’(8, 4), R’(4, 8), and S’(8, 10).So, the correct option is D. P’(12, 6), Q’(8, 4), R’(4, 8), and S’(8, 10).
Step-by-step explanation:
Hope this helps you!! Have a good day/night!!
Gwen and Max had breakfast at a cafe. Muffins cost $2 each, and fruit cups cost $4 each. Gwen had 2 muffins and 1 fruit cup. Max had 2 muffins and 1 fruit cup. How much did their breakfast cost?
Answers
Answer: Gwen's breakfast in total was $8. Max's Breakfast in total is $8 as well. so their breakfast together is $16 in total
Answer:
their breakfast cost 16 dollars
Step-by-step explanation:
because you would do 2 times 2 which is 4 and 1 times 4 which is also 4 add those two together to get 8 and the double it because max got the same thing
(ASAP) What is the measure of angle BDC

Answers
Answer:
105
Step-by-step explanation:
180-75 = 105.
*supplementary angles add up to 180*
Determine the following ratio

Answers
Using relations in a right triangle, the secant of angle θ is given by:
D. 5/4.
What are the relations in a right triangle?The relations in a right triangle are given as follows:
The sine of an angle is given by the length of the opposite side to the angle divided by the length of the hypotenuse.The cosine of an angle is given by the length of the adjacent side to the angle divided by the length of the hypotenuse.The tangent of an angle is given by the length of the opposite side to the angle divided by the length of the adjacent side to the angle.Using the Pythagorean Theorem, the hypotenuse of the triangle is given as follows:
h² = 9² + 12²
h = sqrt(9² + 12²)
h = 15.
The secant of an angle is 1 divided by the cosine, hence:
cos(θ) = 12/15 = 4/5.sec(θ) = 5/4.Which means that option D is correct.
More can be learned about relations in a right triangle at https://brainly.com/question/26396675
#SPJ1
Find a format option that would result in the following output format:
>> 5/16 + 2/7ans = 67/112
Answers
The format option that would result in the following output format:
>> 5/16 + 2/7ans = 67/112 is format compact; format rational; format shortG;
To achieve the desired output format of ">> 5/16 + 2/7ans = 67/112", you can use the following format option in MATLAB:
>> format compact; format rational; format shortG;
This sets the format to:
compact, to suppress excess blank lines in output
rational, to display fractions instead of decimal approximations
shortG, to display numbers in short format
With this format option, MATLAB will display the result of the computation as a fraction, and the output will be compact and free of excessive whitespace.
To learn more about format here:
https://brainly.com/question/27160842
#SPJ4
In a bank, 20 customers on the average, are served by a cashier in an hour. If
the service time has exponential distribution, what is the probability that;
(i) It will take more than 10 minutes to serve a customer?
(ii) A customer shall be free within 4 minutes
Answers
(i) The probability that it will take more than 10 minutes to serve a customer is approximately 0.1353.
(ii) The probability that a customer shall be free within 4 minutes is approximately 0.4866.
To solve this problem, we can use the exponential distribution formula. The exponential distribution is often used to model the time between events occurring at a constant average rate. In this case, we want to find the probability of specific service times.
Let's denote λ as the average number of customers served per hour. Given that 20 customers are served on average, we can determine λ by dividing the average number of customers by the time taken to serve them, which is 1 hour. Therefore, λ = 20 customers/hour.
Now, we can calculate the probability using the exponential distribution formula:
(i) To find the probability that it will take more than 10 minutes to serve a customer, we need to convert 10 minutes to hours, which is 10/60 = 1/6 hour. Let's call this value x.
The probability can be calculated as P(X > x) = 1 - P(X ≤ x), where X follows an exponential distribution with rate parameter λ.
P(X > 1/6) = 1 - P(X ≤ 1/6)
= 1 - (1 - \(e^{(-\lambda x))\) [Using the cumulative distribution function (CDF) of the exponential distribution]
= \(e^(- \lambda x)\)
= \(e^{(-20/6)\)
≈ 0.1353
(ii) To find the probability that a customer shall be free within 4 minutes, we convert 4 minutes to hours, which is 4/60 = 1/15 hour. Let's call this value y.
The probability can be calculated as P(X ≤ y), where X follows an exponential distribution with rate parameter λ.
P(X ≤ 1/15) = 1 - \(e^{(-\lambda y)\)
= 1 - \(e^{(-20/15)\)
≈ 0.4866
Therefore, the probability that a customer shall be free within 4 minutes is approximately 0.4866.
For more such questions on probability, click on:
https://brainly.com/question/251701
#SPJ8
21' 9" - 13' 1"
feet
<
>
Inches
Answers
Answer: 104 inches or 8' 8"
Step-by-step explanation:
1 foot = 12 inches
21 * 12 = 252 inches + 9 = 261 inches
13 * 12 = 156 + 1 = 157 inches
261 - 157 = 104 inches
104 / 12 = 8' 8"
Which scenario best matches the inequality x>3?
A. Joanna needs to be in bed by 10 p.m. It’s now just past 7 p.m. How many more hours, x, can Joanna stay up?
B. Lana stays after school from 3 p.m. until 6 p.m. How many hours, x, does she spend at school during that time frame
C. Ricardo has a math exam. He started studying at 4 p.m. and will not stop until after 7 p.m. How much time, x, will he spend studying?
D. Jared’s baseball game starts at 12 p.m. The game needs to end before 3 p.m. because another team must use the field. How much time, x, can Jared’s team play?
Answers
Answer:
B
Step-by-step explanation:
6TH GRADE MATH SOMEONE PLEASE GIVE ANSWER TYSM

Answers
The surface area of the vase is 168.4 square inches.
What is a cylinder?
A cylinder is a three-dimensional geometric shape that has two congruent circular bases connected by a curved surface.
The surface area of the cylindrical vase can be found using the formula SA = B + Ph, where B is the area of the base, P is the perimeter of the base, and h is the height of the vase. Since the vase has a circular base, the area of the base can be found using the formula for the area of a circle: B = πr², where r is the radius of the base.
The diameter of the vase is 4.3 inches, so the radius is half of that, or 2.15 inches. The area of the base is therefore:
B = πr² = 3.14 * (2.15)² ≈ 14.46 square inches.
The perimeter of the base is the circumference of the circle, which can be found using the formula C = 2πr:
P = 2πr = 2 * 3.14 * 2.15 ≈ 13.53 inches.
Now we can use the formula SA = B + Ph to find the surface area of the vase:
SA = B + Ph = 14.46 + 13.53 * 11 ≈ 168.39 square inches.
Rounding to the nearest tenth of a square inch, the surface area of the vase is approximately 168.4 square inches.
To know more about cylinders visit:
brainly.com/question/15891031
#SPJ1
The monthly rents for five apartments advertised in a newspaper were $650, $650, $800, $1900, and $820. Use the mean, median, and mode of the rents to answer the question. Which value best describes the monthly rents?
Answers
Answer:
The Median Best Describes The Monthly Rents
the mean is add up all the numbers and then divide by the amount of numbers so it is 4820 then divide by 5 = 964 so the mean of all of then is 964
the median you have to put it in slamets to biggest so 650 650 800 820 1900 and then you have to put the one(s) in the middle witch is 800 so the median is 800
the mode is the most common numbers that show up and there is 2 650 and one of everything else so the mode is 650
Hope This Helped
What is the greatest common factor of 42 and 81?
Answers
Answer:
3
Step-by-step explanation:
42 is 2 x 3 x 7
81 is 3 x 3 x 3 x 3
3 is the greatest common factor
Answer:
3
Step-by-step explanation:
3 is the greatest common factor of 42 and 81
If segment AB measures 2 cm, how long is A'B? Explain.
Answers
Transformation involves moving a segment away from its original location.
The length of A'B' is 2cm
The length of AB is given as:
\(AB = 2cm\)
From the complete question, we understand that AB was translated to A'B'
Translation is a rigid transformation.
This means that it does not alter the length of the segment that is being translated.
So, the length of A'B' is represented as:
\(A'B' = AB\)
Substitute 2cm for AB
\(A'B' =2cm\)
Hence, the length of A'B' is 2cm
Read more about transformations at:
https://brainly.com/question/13801312
The function y = 40x describes the distance Shu Ling has traveled in miles after x hours. Use the graph to estimate how many miles Shu Ling will travel in 12 hours.
Answers
Answer: y = 40*12 = 480
Step-by-step explanation:
15.5x{(2 x 2.4)+3.2}-2^4
Answers
Answer:
108
Step-by-step explanation:
I used a calculator
PLS HELP ME WITH THIS QUESTION
PLS SHOW YOUR WORKING OUT

Answers
The formula for y in terms of x and c is given as follows:
\(y = \frac{c^5}{\sqrt{x}}\)
What is a proportional relationship?A proportional relationship is a type of relationship between two quantities in which they maintain a constant ratio to each other. This means that if one quantity is multiplied by a certain factor, the other quantity will also be multiplied by the same factor.
The equation that defines the proportional relationship is given as follows:
y = kx.
In which k is the constant of proportionality, representing the increase in the output variable y when the constant variable x is increased by one.
An inverse proportional relationship is modeled as follows:
y = k/x.
In this problem, we have that y is inverse proportional to the square root of x, hence the equation is given as follows:
\(y = \frac{k}{\sqrt{x}}\)
When x = c², y = c^4, hence the constant k is obtained as follows:
\(c^4 = \frac{k}{\sqrt{c^2}}\)
k/c = c^4
k = c^5.
Hence the equation is:
\(y = \frac{c^5}{\sqrt{x}}\)
More can be learned about proportional relationships at https://brainly.com/question/7723640
#SPJ1
evalute the expression m=4 n=5 and p=-2
n^m
Answers
5 • 5 • 5 • 5 = 625
Answer:
625
Step-by-step explanation:
(5)4
=625
Hope it's help you ❤️❤️❤️❤️❤️❣️❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️
Find the volume of a frustum of a pyramid with square base of side 22, square top of side 13 and height 20.
Answers
The volume of a frustum of a pyramid with given dimensions is 6260 cubic units.
What is frustum of pyramid?
The top of a conventional pyramid is removed to create the frustum, which is a pyramid. It is known as a truncated pyramid for this reason. The height of a pyramid is represented by the letter h and is the distance from its base to its summit. Similar to it, it has two bases and a slant height indicated by the letter "s" (top and bottom).
We are given frustum of a pyramid with square base of side 22, square top of side 13 and height 20.
We know that volume of frustum of pyramid(V) = h(b^2 + a^2 + ab)/3
We are given b = 22, a = 13 and h = 20
From this, we get
⇒V = h(b^2 + a^2 + ab)/3
⇒V = 20(22^2 + 13^2 + 22*13)/3
⇒V = 20(484 + 169 + 286)/3
⇒V = 20(939)/3
⇒V = 20*313
⇒V = 6260 cubic units
Hence, the volume of a frustum of a pyramid with given dimensions is 6260 cubic units.
Learn more about frustum of a pyramid from the given link
https://brainly.com/question/29332606
#SPJ4