Last year, the school library had a total of x books. Over the summer, the library acquired another 35 books and now has a total of 2,943 books. Which equation could be used to find x, the number of books the library had last year?
Answers
Answer:
the equation is x= 2908
Step-by-step explanation:
you need to find the number of books they had by taking the new total and subtract it by the number they add and that would equal x in the problem
Related Questions
2) Find the arc length of the function over the given interval y=x^3/2 from (0,0) to (1,1).
Answers
To find the arc length of the function y = x^(3/2) over the interval from (0,0) to (1,1), we can use the arc length formula for a curve y = f(x) on the interval [a, b]:
L = ∫[a,b] √[1 + (f'(x))^2] dx . First, we need to find the derivative of the function y = x^(3/2). Taking the derivative, we have y' = (3/2)x^(1/2).
Now, let's substitute these values into the arc length formula. The interval is from 0 to 1, so a = 0 and b = 1: L = ∫[0,1] √[1 + ((3/2)x^(1/2))^2] dx. Simplifying the expression inside the square root: L = ∫[0,1] √[1 + (9/4)x] dx.
To find the integral, we can use integration techniques such as substitution or simplification. After evaluating the integral, we will have the arc length of the curve y = x^(3/2) from (0,0) to (1,1). Note: Since the integral expression is a bit complex, it is not possible to provide the exact numerical value without evaluating the integral explicitly.
Learn more about arc here: brainly.com/question/31612770
#SPJ11
what is a = b =c =and y - intercept for the equation y = - 3x^2 + 15
Answers
a=-3, b=0, c=15
y-intercept: 15
1) In this quadratic equation, we can tell the following about their coefficients.
\(a=-3,\:b=0,\:c=15\)2) The y-intercept, in a quadratic equation, is always the coefficient "c". So, we can tell that:
\(y-intercept:\:15\)An oil company purchased an option on land in Alaska. Preliminary geologic studies assigned the following prior probabilities.P(high-quality oil) = 0.50P(medium-quality oil)= 0.20P(no oil) = 0.30If required, round your answers to two decimal places.What is the probability of finding oil?
Answers
Since these are the only two categories that contain oil, the probability of finding oil is the sum of the probabilities of finding high-quality oil and medium-quality oil.
How to calculate and what is probability?Given that to find
P(finding oil) = P(high-quality oil) + P(medium-quality oil)
= 0.50 + 0.20
= 0.70
Thus the probability of finding oil is 0.70, or 70%.
Probability is a measure of how likely an event is to occur. It is a number between 0 and 1, with 0 indicating that the event is impossible and 1 indicating that the event is certain. The probability of an event is calculated by dividing the number of possible outcomes by the number of favourable outcomes.
To know more about probability visit:-
https://brainly.com/question/30034780
#SPJ1
where is the altitude of polaris (the maximum)
Answers
The altitude of Polaris, also known as the North Star, refers to its angle above the horizon when observed from a specific location on Earth.
The altitude of Polaris varies depending on the observer's latitude.
For an observer at the North Pole (latitude 90 degrees), Polaris appears directly overhead, at an altitude of 90 degrees. This means Polaris is at the zenith, the highest point in the sky.
For observers at other latitudes in the Northern Hemisphere, Polaris will appear lower in the sky. The altitude of Polaris is equal to the observer's latitude. For example, if you are at a latitude of 40 degrees north, Polaris will have an altitude of approximately 40 degrees above the horizon.
It's important to note that the altitude of Polaris remains relatively constant throughout the night and throughout the year due to its proximity to the celestial north pole. This makes it a useful navigational reference point for determining direction and latitude in the Northern Hemisphere.
To know more about North Star refer here:
https://brainly.com/question/32168908
#SPJ11
Cody has a bag of 28 pencils. Each pencil is 18 centimeters long. What is the combined length of the pencils in meters?
The total length of all 28 pencils is __ meters.
Answers
Answer:
504
Step-by-step explanation:
Please answer this math question for me? There is two questions in this one picture

Answers
Answer:
the diameter on question 2 is 6. I don't know question 1
Answer:
I dont know for sure so answer as your own risk but I think first one is center of a circle
and second one I believe is 6 Hope that helps!
half of a number is 16. What is the number?
A. 8
B. 4
C. 64
D. 32
Answers
Answer:
32
Step-by-step explanation:
becaus 168 2 is 32
Well...
8+8=16
16+16=32 so the answer is 32 Here's why
So you know that the half of the number is 16 well you would have to add itself so 16+16=32
Hope I could help
Brainlist please?
T is the midpoint of S and U. ST=7x+4 & TU=10x-2. What is the value of SU?
Answers
Answer:
SU = 36
Step-by-step explanation:
T is the mid point so the distance of ST and TU is the same. Since ST and TU are the same, 7x + 4 = 10x - 2.
Solve for x
7x + 4 = 10x - 2
7x - 10x = - 2 - 4
-3x = -6
x = 2.
Find SU
SU = ST + TU
= (7x + 4) + (10x - 2)
substitute the value for x into the equation (x=2)
[7(2) + 4] + [10(2) - 2] = 36
I hope this helps :)
use mathematical induction to prove that if n people stand in a line, where n is a positive integer, and if the first person in the line is a woman and the last person in line is a man, then somewhere in the line there is a woman directly in front of a man.
Answers
In both cases, for a line of k+1 people, there exists a woman directly in front of a man. Thus, by mathematical induction, the statement holds true for all positive integers n where the first person is a woman and the last person is a man.
To prove this statement using mathematical induction, we will first establish a base case. When n = 2, there are only two people in the line, and the statement is true. The first person is a woman and the last person is a man, and therefore the woman is directly in front of the man.
Next, we assume that the statement is true for n = k, where k is a positive integer. That is, if k people stand in a line with a woman first and a man last, then there is a woman directly in front of a man somewhere in the line.
Now, we need to show that the statement is also true for n = k + 1. Suppose k + 1 people stand in a line, with a woman first and a man last. We can remove the first person (the woman) and consider the remaining k people. By our induction hypothesis, there is a woman directly in front of a man somewhere in this line of k people.
Now, we have two cases for the position of the woman and man in the line of k people:
Case 1: The woman directly in front of the man is in the first k positions. In this case, we can add the first person back into the line, and the statement is true for n = k + 1.
Case 2: The woman directly in front of the man is in the last k positions. In this case, we can remove the first person and consider the line of k people from the second person to the last person. By our induction hypothesis, there is a woman directly in front of a man somewhere in this line of k people. When we add the first person back into the line, this woman will be directly in front of the man, and the statement is again true for n = k + 1.
Therefore, by mathematical induction, we have shown that if n people stand in a line, where n is a positive integer, and if the first person in the line is a woman and the last person in line is a man, then somewhere in the line there is a woman directly in front of a man.
Mathematical induction to prove the given statement. We'll use the terms base case, induction hypothesis, and induction step.
Base case (n=2): When there are two people in the line (a woman followed by a man), it's clear that there's a woman directly in front of a man. This establishes our base case.
Induction hypothesis: Assume that for some positive integer k, if there are k people in a line with a woman at the beginning and a man at the end, there exists a woman directly in front of a man.
Induction step: Let's prove this for k+1 people. We have two cases:
1. If the second-to-last person is a woman, we can remove the last man and have a line of k people. By the induction hypothesis, there exists a woman directly in front of a man in this line, and this also holds for the k+1 people line.
2. If the second-to-last person is a man, we can remove the first woman and have a line of k people. By the induction hypothesis, there exists a woman directly in front of a man in this line. When we add back the first woman, she is now directly in front of the second-to-last man, which also satisfies the condition.
In both cases, for a line of k+1 people, there exists a woman directly in front of a man. Thus, by mathematical induction, the statement holds true for all positive integers n where the first person is a woman and the last person is a man.
To learn more about mathematical induction, click here:
brainly.com/question/29503103
#SPJ11
components arriving at a distributor are checked for defects by two different inspectors (each component is checked by both inspectors). the first inspector detects 88% of all defectives that are present, and the second inspector does likewise. at least one inspector does not detect a defect on 24% of all defective components. what is the probability that the following occur?
Answers
The probability that a defective component can be detected by only one inspector is 0.2112. the probability that all three defective components in a batch escape detection by both inspectors is 0.00178.
(a) To calculate the probability that a defective component will be detected by only one inspector, we can use the formula for conditional probability: P(detected by first inspector | not detected by second inspector) = P(detected by first inspector and not detected by second inspector) / P(not detected by second inspector).
The probability that a defective component will be detected by the first inspector and not detected by the second inspector can be calculated as follows: P(detected by first inspector and not detected by second inspector) = P(detected by first inspector) * P(not detected by second inspector | detected by first inspector) = 0.88 * (1 - 0.88) = 0.1056.
The probability that a defective component will not be detected by the second inspector is: P(not detected by second inspector) = 1 - P(detected by second inspector) = 1 - 0.88 = 0.12.
The probability that a defective component will be detected by exactly one of the two inspectors can be calculated as follows: P(detected by exactly one inspector) = P(detected by first inspector and not detected by second inspector) + P(detected by second inspector and not detected by first inspector) = 0.1056 + 0.1056 = 0.2112.
(b) To calculate the probability that all three defective components in a batch escape detection by both inspectors, we can use the formula for independent events: P(all three defective components escape detection) = P(first defective component escapes detection) * P(second defective component escapes detection) * P(third defective component escapes detection) = (1 - 0.88)^3 = 0.00178.
So the probability that all three defective components in a batch escape detection by both inspectors is 0.00178.
Learn more about probability here brainly.com/question/30034780
#SPJ4
Complete question : components arriving at a distributor are checked for defects by two different inspectors (each component is checked by both inspectors). the first inspector detects 88% of all defectives that are present, and the second inspector does likewise. at least one inspector does not detect a defect on 24% of all defective components. what is the probability that the following occur? (a) A defective component will be detected only by the first inspector? A defective component will be detected by exactly one of the two inspectors? (b) All three defective components in a batch escape detection by both inspectors (assuming inspections of different components are independent of one another)?
The area of a rectangle is 26.88 square centimeters. The length of the rectangle is 9.6 centimeters. What is the width of the rectangle in centimeters?
Answers
Answer:
26.88 divided by 9.6 is 2.8
Meaning that the width is 2.8 cm
I can’t figure this out

Answers
its the first one or A
Answer:
The answer to that is the first one :)
Jalisa earned $71.25 today babysitting, which is $22.50 more than she earned babysitting yesterday. The equation d + 22.50 = 71.25 can be used to represent this situation, where d is the amount Jalisa earned babysitting yesterday. Which is an equivalent equation that can be used to find the amount Jalisa earned babysitting yesterday?
Answers
Answer:
A 71.25
Step-by-step explanation:
Answer:
Step-by-step explanation:
The answer is a I took the test

What is the most common error when entering a formula is to reference the wrong cell in the formula?
Answers
The most common error when entering a formula is to reference the wrong cell in the formula.
This error occurs when the cell references within a formula do not match the intended cells. It can lead to incorrect calculations and produce unexpected results. For example, if a formula is supposed to use data from cell A1 but mistakenly refers to cell B1, the calculation will be based on the wrong data. It is important to double-check and ensure that the cell references in a formula accurately reflect the intended data sources to avoid this common mistake.
Know more about cell references here:
https://brainly.com/question/31171096
#SPJ11
Carmen purchased a prepaid phone card for $30. Long distance calls cost 19 cents a minute using this card. Carmen used her card only once to make a long
distance call. If the remaining credit on her card is $26.39, how many minutes did her call last?
Answers
Answer:
19
Step-by-step explanation:
30-26.39=3.61
3.61 divided by 0.19 = 19
hope this helps :)
ANSWER QUICKLY!!!Sal's Sandwich Shop sells wraps and sandwiches as part of its lunch specials. The profit on every sandwich is $2, and the profit on every wrap is $3. Sal made a profit of $1,470 from lunch specials last month. The equation 2x + 3y = 1,470 represents Sal's profits last month, where x is the number of sandwich lunch specials sold and y is the number of wrap lunch specials sold.
(QUESTION!!!)---->Write the equation in function notation. Explain what the graph of the function represents. Be sure to use complete sentences.
Answers
Answer:
f(x)= -2/3x+490
Step-by-step explanation:
The graph of the function represents the amount of money Sal has, as a function of the number of sandwich lunch specials he sells.
Answer:
1. slope intercept form is y=mx+b, where m is the slope and b is y-intercept. To write this in slope intercept form we must isolate the y.
2x+3y=1470
2x+3y-2x=1470-2x( subtraction will cancel the positive 2x on the left side)
3y=-2x+1470 ( since they are not like terms we can not combine them, we leave them separate)
3y/3=-2/3x+1470/3( cancel the 3 by dividing, EVERYTHING IN THE EQUATION gets divided to keep it equal)
So, y=2/3x+490 in other words the slope of the equation is -2/3 and the y-intercept is 490.
2. To graph this equation plot 490 on the y-axis first, seeing it is the y-intercept. Then count over to the right 3 and down 2, to find your next point and do this for every other point.
.3. In function notation this would look like this : f(x)=-2/3x+490. This function shows how the profit on wrap specials has changed as the number of sandwich specials sold increases
5. The next month Sals profit increased. The function changes because the y-intercept changes. The slope will stay the same.
Step-by-step explanation:
Write the equation of the line that passes through the points (7,7) and (-7, -7). Put your answer in fully reduced point-slope form, unless it is a vertical or horizontal line.
Answers
PLEASE help find measure of angle - TEst review today

Answers
Answer:
alternate exterior angles and lines are parallel so
10x is congruent to 11x-8
second question
alternate interior angles and lines are paralles so angles are congruent


for which sample sizes is the first quartile always equal to one of the values in the sample?
Answers
The first quartile is always equal to one of the values in the sample when the sample size is a multiple of 4.
This is because the first quartile is the median of the lower half of the data set, and when the sample size is a multiple of 4, there is anThe first quartile is always equal to one of the valuesin the sample when the sample size is a multiple of 4. This is because the first quartile is the median of the lower half of the data set, and when the sample size is a multiple of 4, there is an even number of values in the lower half of the data set. Therefore, the first quartile will be one of the values in the sample. For example, if the sample size is 8, the first quartile will be the median of the first 4 values, which will be one of the values in the sample.
In summary, the first quartile is always equal to one of the values in the sample when the sample size is a multiple of 4. of values in the lower half of the data set. Therefore, the first quartile will be one of the values in the sample. For example, if the sample size is 8, the first quartile will be the median of the first 4 values, which will be one of the values in the sample.
In summary, the first quartile is always equal to one of the values in the sample when the sample size is a multiple of 4.
Read more about quartile here:https://brainly.com/question/28277179
#SPJ11
Please help! offering 25 points, 5 stars, and a thanks. Ive asked this 3 times now

Answers
Answer:
17 quarters
Step-by-step explanation:
Let q = quarters
n = nickels
.25q + .05n = 5.90
we have 16 more nickels than quarters so add 16 quarters to make them equal
n = q+16
Substitute
.25q + .05( q+16) = 5.90
Distribute
.25q+.5q+.80=5.90
Combine like terms
.30q +.8 = 5.90
Subtract .8 from each side
.30q = 5.10
Divide each side by .3
.3q/.3 = 5.1/.3
q = 17
Answer:
Gisel have:
17
quarters
Step-by-step explanation:
1 nickel = 5 cents
1 quarter = 25 cents
1 dollar = 100 cents
5,90 dollars = 5,9*100 = 590 cents
then:
n = t + 16
5n + 25t = 590
n = quantity of nickels
t = quantity of quarters
5(t+16) + 25t = 590
5*t + 5*16 + 25t = 590
5t + 80 + 25t = 590
30 t = 590 - 80
30 t = 510
t = 510 / 30
t = 17
n = t + 16
n = 17 + 16
n = 33
Check:
5n + 25t = 590
5*33 + 25*17 = 590
165 + 425 = 590
Someone help me solve just these two questions
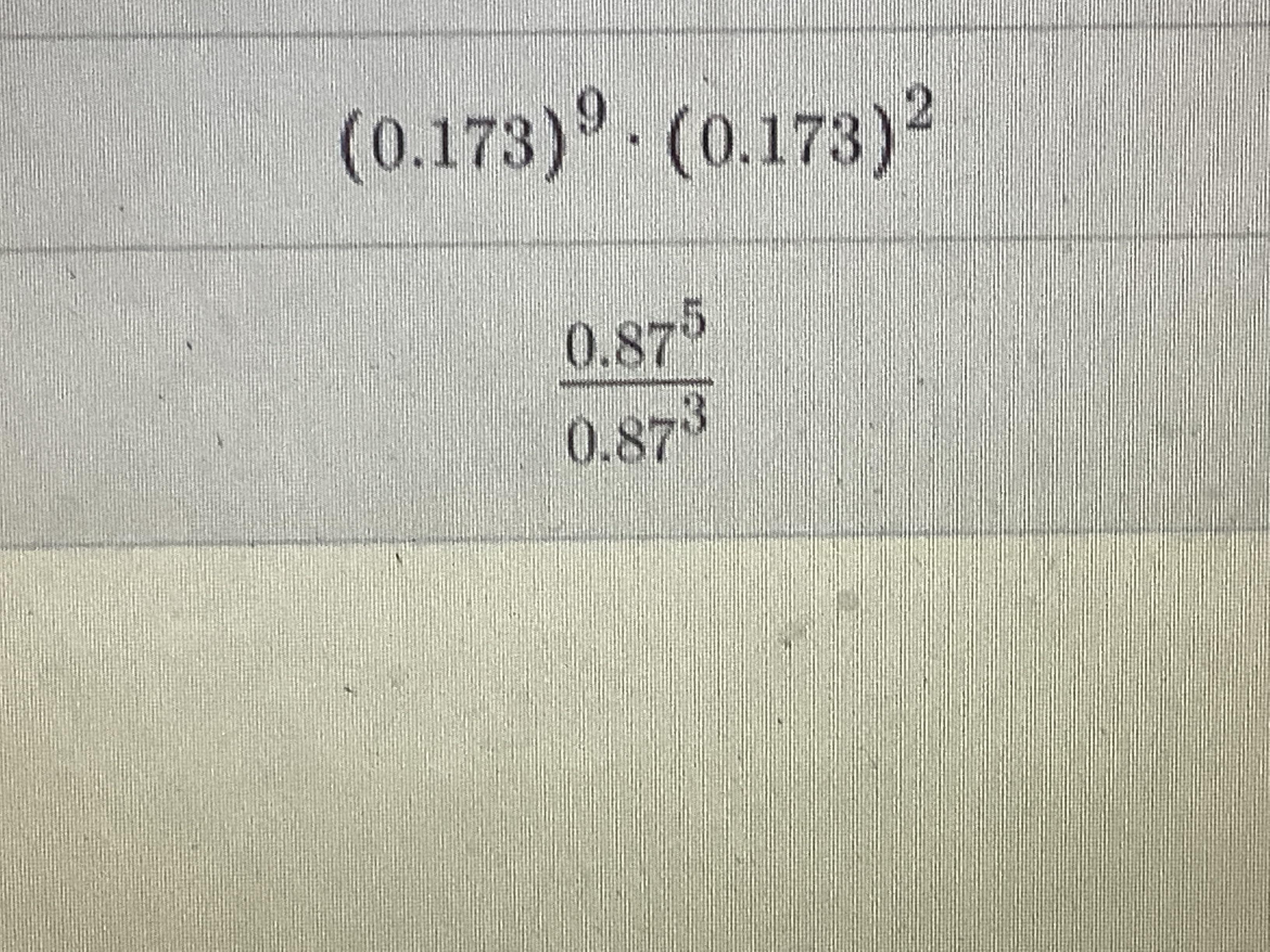
Answers
Answer:
(0.173)¹¹(0.87)²Step-by-step explanation:
Q1
(0.173)⁹ × (0.173)² When two terms with equal bases with different powers are multiplied, it is equal to the base with the sum of the powers(0.173)⁹⁺² (0.173)¹¹Q2
0.87⁵/0.87³When two terms with equal bases with different powers are divided, it is equal to the base with the difference of the powers(0.87)⁵⁻³(0.87)²Let D be a constant tensor whose components do not depend upon the coordinates. Show that
(x ⋅D) = D
where x =xi eˆi is the position vector.
Answers
To prove (x ⋅ D) = D, we can use the definition of the dot product and the fact that D is a constant tensor with components that do not depend on the coordinates.
Let x = xi eˆi be the position vector and let D have components Dij. Then, we have:
(x ⋅ D)i = xjDij
Using the summation convention, we can write this as:
(x ⋅ D)i = xiDii
Since D is a constant tensor, we know that Dii = D for all i. Therefore:
(x ⋅ D)i = xiD
Thus, we have shown that (x ⋅ D) = D, as required.
Learn more about Vectors:
https://brainly.com/question/25705666
#SPJ4
The position of a particle moving along the x-axis is given by x(t) = t^3 + 9t^2 − 21t with t is in [0, 2].
(a) Find the velocity and acceleration of the particle.
(b) For what t-values is the velocity 0? (Enter your answers as a comma-separated list.)
(c) When is the particle moving to the left (velocity is negative)? (Enter your answer using interval notation.)
When is the particle moving to the right (velocity is positive)? (Enter your answer using interval notation.) (
d) What is the farthest the particle gets to the left? What is the farthest the particle gets to the right?
(e) When is the velocity increasing? (Enter your answer using interval notation. If an answer does not exist, enter DNE.) When is the velocity decreasing? (Enter your answer using interval notation. If an answer does not exist, enter DNE.)
(f) What is the maximum velocity of the particle? v =
Answers
Therefore, the particle is moving to the right on the intervals (−∞, -7) and (1, ∞) and to the left on the interval (−7, 1).
(a) Velocity is the first derivative of position.
Thus, we have;
vx(t) = x'(t) = 3t² + 18t − 21a(t)
= v'(t) = 6t + 18
(b) Setting the velocity function to zero:vx(t) = 3t² + 18t − 21 = 0 ⇒ t² + 6t − 7 = 0 (t + 7)(t − 1) = 0t = −7, 1.
Thus, the velocity is zero at t = -7 and t = 1.
(c) From the velocity function, we see that:v(t) > 0 on the intervals (−∞, -7) and (1, ∞)v(t) < 0 on the interval (−7, 1).
Therefore, the particle is moving to the right on the intervals (−∞, -7) and (1, ∞) and to the left on the interval (−7, 1).
(d) The position of the farthest point to the left is found as the minimum value of the position function in the interval [0,2].
The position of the farthest point to the right is found as the maximum value of the position function in the interval [0,2].
The minimum value of x(t) is:
x(7/3) = (7/3)³ + 9(7/3)² − 21(7/3) = −107/27
The maximum value of x(t) is:x(2) = 2³ + 9(2)² − 21(2) = 7
(e) Acceleration is the derivative of the velocity. The acceleration is given as a(t) = 6t + 18vx(t) is increasing when vx'(t) > 0vx'(t) = 6t + 18 > 0
⇒ t > −3vx(t) is decreasing when vx'(t) < 0vx'(t) = 6t + 18 < 0
⇒ t < −3
Thus, the velocity is increasing on the interval (−3, ∞) and is decreasing on the interval (−∞, −3).
(f) The maximum velocity of the particle is found at the critical points of the velocity function. The velocity function has critical points at t = −7 and t = 1vx(−7) = 0 and vx(1) = 0vx(t) is increasing on the interval (−7, 1) and is decreasing on the interval (−∞, −7) ∪ (1, ∞).
Thus, the maximum velocity of the particle is vx(1) = 0.
vx(t) = 3t² + 18t − 21a(t) = 6t + 18vx(1) = 0t = −7, 1v(t) > 0 on the intervals (−∞, -7) and (1, ∞)v(t) < 0 on the interval (−7, 1)
The farthest point to the left is at t = 7/3
The farthest point to the right is at t = 2vx(t) is increasing on the interval (−3, ∞) and is decreasing on the interval (−∞, −3).
Maximum velocity is 0.
To know more about velocity,
https://brainly.com/question/80295
#SPJ11
What is the solution to the following system of equations
4x+2y=6
X-y=3

Answers
Answer:
The solution of the equation 4x + 2y = 6 and x − y = 3 will be D. (2, –1)
Step-by-step explanation:
4x + 2y = 6 ....… (1)
x − y = 3 …..... (2)
Example, for equation 2 is:
x - y = 3
x = 3 + y
Put in equation 1:
4(y + 3) + 2y = 6
4y + 12 + 2y = 6
6y = -6
y = -6/6
y = -1
We have the value of y, then the value of x will be:
x = 3 + y
= 3 + (-1)
= 3 - 1
= 2
So, the solution of the equation 4x + 2y = 6 and x − y = 3 will be (2, –1)
Aman is graduating from college and looking forward to his new role in his job as a computer scientist for a large firm. This is an example of
Answers
The answer is B. anticipatory socialization. Aman's anticipation and excitement about his new role as a computer scientist indicate his engagement in anticipatory socialization.
Anticipatory socialization refers to the process through which individuals learn and internalize the values, norms, and behaviors associated with a future role or status they aspire to have. In this case, Aman's graduation from college and his upcoming job as a computer scientist represent a transition to a new role.
As he looks forward to this new position, he is likely engaging in activities such as researching the company, learning about the responsibilities of a computer scientist, and acquiring the necessary skills to excel in his job. By doing so, Aman is preparing himself and adjusting his attitudes and behaviors to fit the expectations of his future role, which characterizes anticipatory socialization.
Learn more about anticipatory socialization here:
https://brainly.com/question/32050760
#SPJ11
The complete question is:
Aman is graduating from college and looking forward to his new role in his job as a computer scientist for a large firm. This is an example of
A.the imagination stage
B.anticipatory socialization.
C.the game stage.
D.looking-glass self
please help me please

Answers
Answer:
b I think.
Step-by-step explanation:
sorry if im wrong
The current stock price of khhnon 8 - solvnson ப6) is $178, and the stock does not pyy dividends. The instantarnoun the liren rate of return is 6%. The instantaneous standard deviation of J. J's stock is 30% You want to purchate a put option on thik woek with an evercise nrice of $171 and an expiration date 60 davs from now. Assume 365 davt in a year. With this intermation. you the N(d2) as 0.63687 Using Black-Schales, the put option should be worth today.
Answers
The put option should be worth $8.11 The current stock price of khhnon 8 - solvnson ப6) is $178 Instantaneous rate of return is 6% Instantaneous standard deviation of J.
J's stock is 30%Strike price is $171 Expiration date is 60 days from now The formula for the put option using the Black-Scholes model is given by: C = S.N(d1) - Ke^(-rT).N(d2)
Here,C = price of the put option
S = price of the stock
N(d1) = cumulative probability function of d1
N(d2) = cumulative probability function of d2
K = strike price
T = time to expiration (in years)
t = time to expiration (in days)/365
r = risk-free interest rate
For the given data, S = 178
K = 171
r = 6% or 0.06
T = 60/365
= 0.1644
t = 60N(d2)
= 0.63687
Using Black-Scholes, the price of the put option can be calculated as: C = 178.N(d1) - 171.e^(-0.06 * 0.1644).N(0.63687) The value of d1 can be calculated as:d1 = [ln(S/K) + (r + σ²/2).T]/σ.
√Td1 = [ln(178/171) + (0.06 + 0.30²/2) * 0.1644]/(0.30.√0.1644)d1
= 0.21577
The cumulative probability function of d1, N(d1) = 0.58707 Therefore, C = 178 * 0.58707 - 171 * e^(-0.06 * 0.1644) * 0.63687C = 104.13546 - 96.02259C
= $8.11
Therefore, the put option should be worth $8.11.
To know more about stock price visit:
https://brainly.com/question/18366763
#SPJ11
Can someone make sure that the first one is right and can someone help me with the second one please I need to get this right please

Answers
Answer:
1. B
2. A
Step-by-step explanation:
1. Here, the figure is reflected over the line depicted. This answer is correct.
2. Here the image shifts down and across, making it a glide.
a student takes a true-false test that has 14 questions and guesses randomly at each answer. let x be the number of questions answered correctly. find p(5)
Answers
The probability of answering 5 questions correctly on a true-false test with 14 questions when guessing randomly, or P(5), is 0.155 (or 15.5%).
To find P(5), the probability of answering 5 questions correctly on a true-false test with 14 questions when guessing randomly, we can use the binomial probability formula:
P(x) = C(n, x) * p^x * q^(n-x)
Where:
n is the number of trials (14 questions)
x is the number of successful outcomes (5 correct answers)
p is the probability of success (0.5 for random guessing on a true-false test)
q is the probability of failure (1 - p, which is also 0.5 for a true-false test)
Plugging in the values, we have:
P(5) = C(14, 5) * (0.5)^5 * (0.5)^(14-5)
Using the binomial coefficient C(14, 5) = 2002, we calculate:
P(5) = 2002 * (0.5)^5 * (0.5)^9
P(5) = 2002 * 0.5^14
P(5) ≈ 0.155
Learn more about probability here:
https://brainly.com/question/29782219
#SPJ11
Find 3[g(4)] if g(x) = -2x + 10
Answers
Answer:
6
Step-by-step explanation:
= 3[-2(4) + 10]
= 3(-8 + 10)
= 3(2)
The function is given as g(x) = -2x + 10 then the solution of the 3[g(4)] would be equal to 6.
What is a function?A function is a type of relation, or rule, that maps one input to a specific single output.
Functions that are formed by composing two or more functions in a way that one's output is another's input are called composite functions.
They are also called functions of functions.
We have to find 3[g(4)] if g(x) = -2x + 10
3[g(4)] = 3[-2(4) + 10]
3[g(4)] = 3(-8 + 10)
3[g(4)] = 3(2)
3[g(4)] = 6
Learn more about function here:
https://brainly.com/question/2253924
#SPJ2