Let n≥3. A list of numbers x1,x2,.....xn has mean μ and standard deviation σ. A new list of numbers y1,y2,....yn is made as follows : y1=2x1+x2,y2=2x1+x2 and yj=xj for j=3,4,....n. The mean and the standard deviation of the list are μ^ and σ^. Then which of the following is necessarily true?A μ=σ^ and σ≤σ^B μ=μ^ and σ≥σ^C σ=σ^D μ=μ^
Answers
The question is asking which of the following statements is necessarily true regarding the mean and standard deviation of a list of numbers after a transformation is applied. To answer this, we must consider the transformations that were applied and the definitions of mean and standard deviation.
Mean (μ) is the average of all the numbers in the list, calculated by summing all the numbers and dividing by the total number of numbers in the list. Standard Deviation (σ) is a measure of how spread out the numbers in the list are, calculated by finding the square root of the average of the squares of the differences between each number in the list and the mean.
The transformation applied to the list of numbers is y1=2x1+x2,y2=2x1+x2 and yj=xj for j=3,4,....n. We can see from this that the first two numbers in the new list will have their values multiplied by 2 and added together, while the remaining numbers in the list will have their values remain unchanged. This means that the mean and standard deviation of the new list will remain unchanged.
Therefore, the correct answer is Option C: σ=σ^. Since the mean and standard deviation of the new list remain unchanged after the transformation, they will both equal the same values they had before the transformation, i.e. μ=μ^ and σ=σ^.
To know more about mean and standard deviation refer here:
https://brainly.com/question/28108712
#SPJ11
Related Questions
lmn is straight line coordinates of L (-3,1) coordinates of M (4,9) LM:MN is 2:3 find coordinates of N
Answers
The coordinates of point N are (8.66, 21)
What is the general equation of a Straight line? What is Section Formula in 2 - D geometry?The general equation of a straight line is -
[y] = [m]x + [c]
where -
[m] is slope of line which tells the unit rate of change of [y] with respect to [x].
[c] is the y - intercept i.e. the point where the graph cuts the [y] axis.
The coordinates of a point dividing a straight line joining two coordinates in the ratio m : n is given by -
x = \($\frac{mx_2+nx_1}{m+n}\)
y = \($\frac{my_2+ny_1}{m+n}\)
We have LMN as a straight line such that the coordinates of L are (-3,1) , coordinates of M are (4,9) and LM : MN is 2 : 3.
Assume the coordinates of point N are (a, b).
We can write -
9 = (2b + 3)/5
4 = (-6 + 3a)/5
2b + 3 = 45
b = 21
3a - 6 = 20
3a = 26
a = 8.66
Therefore, the coordinates of point N are (8.66, 21)
To solve more questions on section formula, visit the link below -
brainly.com/question/25377004
#SPJ1
how do you do this question

Answers
Answer:
Look at the explanation
Step-by-step explanation:
Type of angle pair: parallel angle pair
These angles are: corresponding angles
So, x = 68°
Suppose that scores on an exam are normally distributed with mean 80 and standard deviation 5, and that scores are not rounded. a a. What is the probability that a student scores higher than 85 on the exam? b. Assume that exam scores are independent and that 10 students take the exam. What is the probability that 4 or more students score 85 or higher on the exam?
Answers
a. The probability that a student scores higher than 85 on the exam can be calculated using the standard normal distribution and the given mean and standard deviation.
b. The probability that 4 or more students score 85 or higher on the exam can be calculated using the binomial distribution, assuming independence of the exam scores and using the probability calculated in part (a).
a. To find the probability that a student scores higher than 85 on the exam, we need to calculate the area under the normal distribution curve to the right of the score 85.
By standardizing the score using the z-score formula, we can use a standard normal distribution table or a statistical calculator to find the corresponding probability.
The z-score is calculated as (85 - mean) / standard deviation, which gives (85 - 80) / 5 = 1. The probability of scoring higher than 85 can be found as P(Z > 1), where Z is a standard normal random variable.
This probability can be looked up in a standard normal distribution table or calculated using a statistical calculator.
b. To calculate the probability that 4 or more students score 85 or higher on the exam, we can use the binomial distribution. The probability of a single student scoring 85 or higher is the probability calculated in part (a).
Assuming independence among the students' scores, we can use the binomial probability formula: P(X ≥ k) = 1 - P(X < k-1), where X is a binomial random variable representing the number of students scoring 85 or higher, and k is the number of students (4 in this case). We can then plug in the values into the formula and calculate the probability using a statistical calculator or software.
To learn more about standard deviation visit:
brainly.com/question/13498201
#SPJ11
Which expression shows the result of applying the distributive property to −2(13x−15)?
Answers
I need help with this one too


Answers
The two column proof is completed as follows
Statement Reason
1 DE bisects /BDC Given
DE bisects angle BEC Given
2. angle BDE ≅ angle CDE An angle bisector divides an angle into
two congruent angles
3. angle BED ≅ angle CED An angle bisector divides an angle into
two congruent angles
4. line DE ≅ line DE Reflexive Property
5. Δ BDE ≅ Δ CDE ASA
6. line BE ≅ line CE Corresponding Parts of Congruent
Triangles are Congruent (CPCTC)
7. line AE ≅ line AE Reflexive Property
8. Δ AEB ≅ Δ AEC SAS
9. ∠ ABE ≅ ∠ ACE Corresponding Parts of Congruent
Triangles are Congruent (CPCTC)
What is ASA?In geometry, ASA stands for "angle-side-angle" and refers to a method of proving that two triangles are congruent.
To prove that two triangles are congruent using the ASA postulate, you need to show that:
Two angles of one triangle are congruent to two angles of the other triangle.The included sides (the sides between the two congruent angles) are also congruent.In the problem the included side is line DE
Learn more about ASA at:
https://brainly.com/question/3999145
#SPJ1
If the diameter of a circle is 46 centimeters long, how long is the radius of the circle?
OA. 184 centimeters
OB B. 11.5 centimeters
OC. 92 centimeters
OD. 23 centimeters
Answers
Answer:
r = 23
Step-by-step explanation:
Using the formula
d = 2rSolving for r
r = d / 2 = 46 / 2 = 23T/F: an example of a weight used in the calculation of a weighted index is quantity consumed in a base period.
Answers
False. The quantity consumed in a base period is not an example of a weight used in the calculation of a weighted index.
In the calculation of a weighted index, a weight is a factor used to assign relative importance or significance to different components or categories included in the index. These weights reflect the contribution of each component to the overall index value. The purpose of assigning weights is to ensure that the index accurately reflects the relative importance of the components or categories being measured.
An example of a weight used in a weighted index could be market value, where the weight is determined based on the market capitalization of each component. This means that components with higher market values will have a greater weight in the index calculation, reflecting their larger impact on the overall index value.
On the other hand, the quantity consumed in a base period is not typically used as a weight in a weighted index. Instead, it is often used as a reference point or benchmark for comparison. For example, in a price index, the quantity consumed in a base period is used as a constant quantity against which the current prices are compared to measure price changes.
Therefore, the statement that the quantity consumed in a base period is an example of a weight used in the calculation of a weighted index is false.
To learn more about weight, click here:
brainly.com/question/19053239
#SPJ1
Which two triangles below are similar?
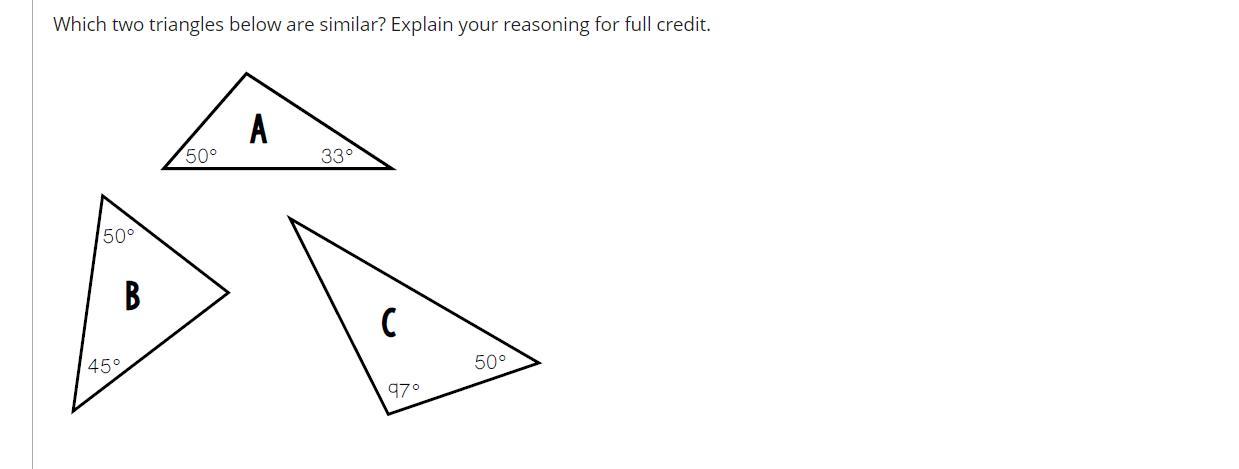
Answers
Answer:
Triangle A and B
Step-by-step explanation:
Both triangles have two same angles.
If Triangle A is rotated like Triangle B, they would be the same.
Vice versa, if Triangle B is rotated like Triangle A, it would be the same.
If my answer is incorrect, pls correct me!
If you like my answer and explanation, mark me as brainliest!
-Chetan K
Given that BD is both the median and altitude of ABC, congruence postulate
SAS is used to prove that ABC is what type of triangle?

Answers
Answer:
isosceles
Step-by-step explanation:
An isosceles triangle is one with two equal-length sides. The correct option is D.
What is an isosceles triangle?An isosceles triangle is one with two equal-length sides. It is sometimes stated as having exactly two equal-length sides, and sometimes as having at least two equal-length sides, with the latter form containing the equilateral triangle as a particular case.
Any triangle, whose median is also the altitude of the triangle is an isosceles triangle. Since it is given that BD is both the median and altitude of ΔABC. Therefore, the given ΔABC is an isosceles triangle.
Learn more about Isosceles Triangle:
https://brainly.com/question/2456591
#SPJ5
Un lote con forma cuadrada tiene una superficie de LaTeX: \sqrt{\frac{4225}{16}\:\:\:\:m^2}\:\:\:\:\:. Si el dueño del lote quiere colocar 3 hileras de alambres alrededor del terreno, ¿cuantos metros necesitará?
Answers
Answer:
The owner needs 195 meters of wire
Step-by-step explanation:
If the lot is squared shaped, then its area is given by the formula:
\(Area =x^2\)
where x is the side of the square. Then considering the value they provide for the surface, each side must be of length:
\(x^2=\frac{4225}{16} \,m^2\\x=\sqrt{\frac{4225}{16}} \,\,m\\x=16.25\,\,m\)
Then the perimeter around this square lot is four times that side length:
Perimeter = 4 (16.25 m) = 65 m
and since the owner wants three rows of wire, the total length of wire needed is:
3 (65 m) = 195 m
Andrea has 6 hours to spend training for an upcoming race. She completes her training by running full speed the distance of the race and walking back the same distance to cool down. If she runs at a speed of 7mph and walks back at a speed of 3mph, how long should she plan to spend walking back
Answers
Andrea should plan to spend 4.2 hours walking back.
Let's start by finding the total distance Andrea runs. Since she runs the full distance of the race and then walks back the same distance, the total distance she covers is twice the race distance.
Let D be the race distance. Therefore, the total distance Andrea covers is 2D.
Next, we can use the formula:
time = distance / speed
The time it takes for Andrea to run the race distance at a speed of 7mph is:
time to run = D / 7
Similarly, the time it takes for Andrea to walk back the same distance at a speed of 3mph is:
time to walk = D\3
The total time Andrea spends training is 6 hours, so we can write:
time to run + time to walk = 6
Substituting the expressions for time to run and time to walk, we get:
D / 7 + D / 3 = 6
We can simplify this equation by finding a common denominator for the fractions:
(3D + 7D) / (3 × 7) = 6
10D / 21 = 6
Multiplying both sides by 21:
10D = 126
D = 12.6 miles
Now that we know the race distance, we can find the time it takes Andrea to walk back:
time to walk = D / 3 = 12.6 / 3 = 4.2 hours
for such more question on hours
https://brainly.com/question/17146782
#SPJ11
If P(B)=0.3,P(A∣B)=0.5,P(B ′ )=0.7, and P(A∣B ′ )=0.8, find P(B∣A).
Answers
If P(B)=0.3, P(A|B)=0.5, P(B')=0.7and P(A|B')=0.8, then the value of the probability P(B|A)= 0.2113
To find the value of P(B|A), follow these steps:
The probability of B given A can be given by the product of the probability of A given B and the probability of B, divided by the total probability of B. So, the formula for P(B|A) = P(A|B) * P(B) / [P(A|B)*P(B)+P(A|B')*P(B')]. Substituting the values, we get P(B|A) = (0.5) (0.3) / [(0.5) (0.3) + (0.8) (0.7)] ⇒P(B|A) = 0.15 / [0.15 + 0.56] ⇒P(B|A) = 0.15 / 0.71 ⇒P(B|A) = 0.2113. Therefore, P(B|A) = 0.2113.Learn more about probability:
brainly.com/question/13604758
#SPJ11
Find the volume of the prism, using a calculator if necessary.
4 cm
9 cm
5 cm
5 cm
12 cm
Answers
Answer:
where is the drawing l don't understand the measurements
ujalakhan01 can you answer these? 1. In Spencer’s garden, the number of rose bushes is 7 less than 1.5 times the number of carnation bushes. If the number of carnation bushes is c, then the expression representing the number of rose bushes is 2. Using the Distributive Property, the expression 9.78(4.3x + 5.15) simplifies to

Answers
Answer:
B
42.05x + 50.36
Step-by-step explanation:
1. It is 1.5c - 7 because tje mumber of rose bushes is 7 less that 1.5(c), not 1.5(7). So, it is (b).
2. 9.78(4.3x + 5.15)
42.05x + 50.36
Hope this helps:)
P.S. I am not ujalakhan01:(
Bill and his friends were super thirsty. They went to the store and bought a bunch of Gatorades for $4 each. They spent $20. How many Gatorades did they buy
Answers
Bill and his friends were thirsty and decided to buy Gatorade at the store. The cost of each bottle of Gatorade was $4. Bill and his friends spent $20 in total. Therefore, we can find out how many bottles of Gatorade they purchased by dividing the total amount spent by the cost per bottle. We can express this relationship as:
$$Total\ cost\ =\ Price\ per\ unit \times Quantity$$This relationship is also known as the cost-volume relationship. The cost-volume relationship indicates how changes in the quantity of goods or services purchased affect the total cost. Using the cost-volume relationship, we can find out how many bottles of Gatorade Bill and his friends purchased.
If they spent $20 in total, and each bottle of Gatorade cost $4, we can express this relationship as: $$20 = 4 \times Quantity$$where Quantity represents the number of bottles of Gatorade purchased. Solving for Quantity, we can divide both sides of the equation by 4: $$Quantity = 20/4 = 5$$Therefore, Bill and his friends bought 5 bottles of Gatorade.
To know more about dividing visit:
https://brainly.com/question/15381501
#SPJ11
The equation is y=
Graph of f(x)= |x|

Answers
The equation from the given graph is y=-2/3 x²+5.
From the given graph the vertex is (h, k)=(0, 5).
What is quadratic equation of graph?A quadratic function is one of the form f(x) = ax² + bx + c, where a, b, and c are numbers with a not equal to zero. The graph of a quadratic function is a curve called a parabola.
The vertex form of a quadratic function is f(x) = a(x - h)² + k, where (h, k) is the vertex of the parabola. The coefficient a determines whether the graph of a quadratic function will open upwards or downwards.
Here, point on the given line from the graph is (3, -1)
Put (x, y)=(3, -1) and (h, k)=(0, 5) in y = a(x - h)² + k, we get
-1=a(3-0)²+5
⇒ 9a=-6
⇒ a=-2/3
Now, y=-2/3(x-0)²+5
y=-2/3 x²+5
Hence, the equation from the given graph is y=-2/3 x²+5.
To learn more about the quadratic function visit:
https://brainly.com/question/27918223.
#SPJ1
binomial a lottery will be held. from 1000 numbers, one will be chosen as the winner. a lottery ticket is a number between 1 and 1000. how many tickets do you need to buy in order for the probability of winning to be at least 50%?
Answers
we need to buy at least 694 tickets to have a probability of winning at least 50%.
We can use the binomial distribution formula to solve this problem. Let X be the number of tickets we need to buy to have a probability of winning at least 50%. Then:
P(X ≥ 1) ≥ 0.5
This means that the probability of winning with at least one ticket is at least 50%. We can find this probability using the complement rule:
P(X ≥ 1) = 1 - P(X = 0)
The probability of not winning with any ticket is:
P(X = 0) = (999/1000)^n
where n is the number of tickets we buy. Therefore:
1 - (999/1000)^n ≥ 0.5
Simplifying this inequality, we get:
(999/1000)^n ≤ 0.5
Taking the logarithm of both sides, we get:
n log(999/1000) ≤ log(0.5)
n ≥ log(0.5) / log(999/1000)
n ≥ 693.15
Therefore, we need to buy at least 694 tickets to have a probability of winning at least 50%.
Learn more about Probability
brainly.com/question/30034780
#SPJ11
according to government data, 22% of american children under the age of six live in households with incomes less than the official poverty level. a study of learning in early childhood chooses an srs of 300 children. find the probability that more than 20% of the sample are from poverty households. be sure to check that you can use the normal approximation.
Answers
The probability that more than 20% of the sample are from poverty households is approximately 0.8365.
What is the probability?
Probability is simply how likely something is to happen. Whenever we're unsure about the outcome of an event, we can talk about the probabilities of certain outcomes—how likely they are. The analysis of events governed by probability is called statistics.
We can use the normal approximation to the binomial distribution to solve this problem, given that the sample size is relatively large (n=300) and the probability of success (p=0.22) is not too close to 0 or 1.
Let X be the number of children in the sample who live in poverty households. Then X follows a binomial distribution with parameters n=300 and p=0.22.
The mean of X is given by μ = np = 300 x 0.22 = 66, and the standard deviation is σ = sqrt(np(1-p)) = sqrt(300 x 0.22 x 0.78) ≈ 6.23.
We want to find the probability that more than 20% of the sample are from poverty households, which is equivalent to finding P(X > 0.2n) = P(X > 60).
To use the normal approximation, we can standardize X as follows:
Z = (X - μ) / σ
Then, we have:
P(X > 60) = P(Z > (60 - 66) / 6.23) ≈ P(Z > -0.96)
Using a standard normal table or calculator, we can find that the probability of Z being greater than -0.96 is approximately 0.8365.
Therefore, the probability that more than 20% of the sample are from poverty households is approximately 0.8365.
To learn more about the probability visit:
https://brainly.com/question/13604758
#SPJ1
what is the answer???????
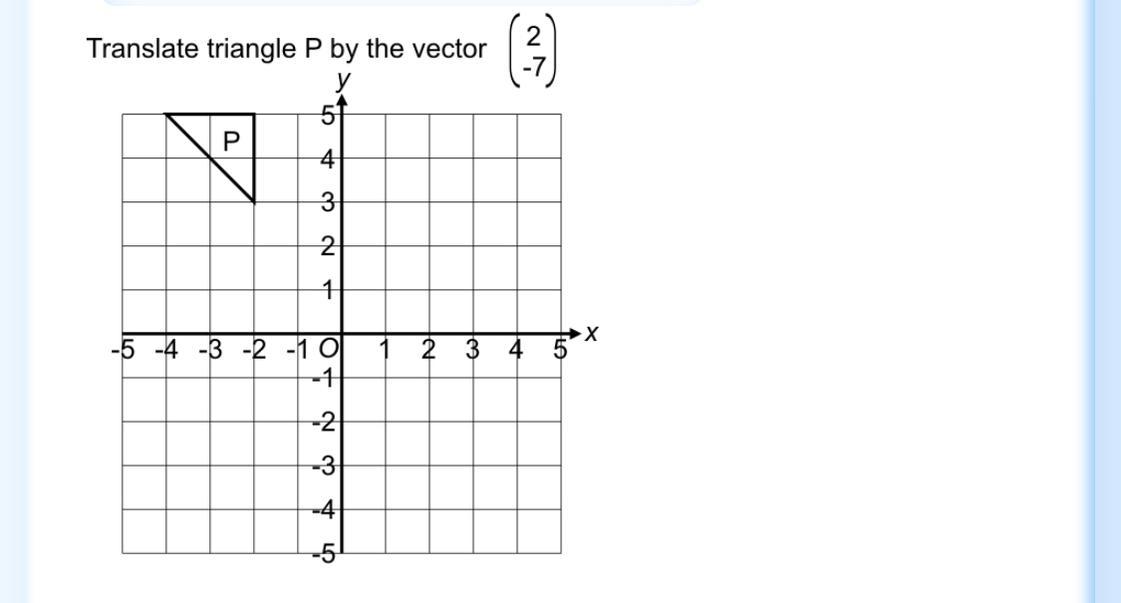
Answers
Answer: Where P is.
Step-by-step explanation
Show your work. please

Answers
Answer:
Opposite angles are equal
3x + 30 =162
-30
3x=132
÷3
x=44
3x44+30=162
Answer: 44
When two straight lines intersect, the opposite angles are equal... So we can create a formula with this that:
3x + 30 = 162 ( solve for x )
3x = 162 - 30
x = 132/3
x = 44
So the value of x is 44!
Brainliest please if I could make it clear for you! <3
2x^2 + 8x factor out the gcf
Answers
Answer:
2x(x + 4)
Step-by-step explanation:
The greatest common factor of 2x^2 and 8x is 2x. So, we can factor out 2x to get:
2x(x + 4)
The definition of a greatest common factor (GCF) is the largest number that is a factor of two or more numbers. In this case, 2x is the GCF of 2x^2 and 8x because it is the largest number that divides both numbers evenly.
Here are the steps on how to factor out the GCF:
Find the GCF of the two numbers. In this case, the GCF is 2x. Write the GCF as a factor of each number. Combine the factors to get the factored expression.In this case, the factored expression is 2x(x + 4).
The answer is:
⇨ 2x(x + 4)Work/explanation:
Let's find something that \(\sf{2x^2}\) and \(\sf{8x}\) have in common.
In other words, we find their GCF (greatest common factor).
The GCF of \(\sf{2x^2}\) and \(\sf{8x}\) is 2x.
So I factor it out :
\(\sf{2x(x+4)}\)
Hence, the answer is 2x(x + 4).I've forgotten how to do this! Please help meee

Answers
Answer:
x<13
Step-by-step explanation:
4x+12<64
Subtract 12 from both sides.
simplify 64 to 52.
Divide both sides by 4.
simplify 52/4 to 13
list and describe two specialized alternatives not often used as a continuity strategy. quizlet
Answers
1. P-adic Numbers:
P-adic numbers are a specialized alternative not commonly used as a continuity strategy in mathematics. They are an extension of the real numbers that provide a different way of measuring and analyzing numbers. P-adic numbers are based on a different concept of distance, known as the p-adic metric. This metric assigns a measure of closeness or distance between numbers based on their divisibility by a prime number, p. P-adic numbers have unique properties and can be useful in number theory, algebraic geometry, and other branches of mathematics. However, they are not typically employed as a continuity strategy in practical applications.
2. Nonstandard Analysis:
Nonstandard analysis is a mathematical framework that provides an alternative approach to calculus and analysis. It introduces new types of numbers called "infinitesimals" and "infinite numbers" that lie between the standard real numbers but are infinitely smaller or larger than any real number. Nonstandard analysis allows for more rigorous treatment of infinitesimal quantities and provides a different perspective on limits, continuity, and differentiation. While nonstandard analysis has theoretical implications and can provide valuable insights in mathematical research, it is not commonly used as a continuity strategy in practical applications where standard analysis and calculus are more prevalent.
To learn more about alternatives in mathematics click here brainly.com/question/17199039 #SPJ11
How many solutions does the following system of linear equations have?
6(x + 4) = 2(3x + 4)
Answers
6x + 24 = 6x + 8
Cancel equal terms
24=8
the statement is false(Ø)
A quarterback's pass completion percentage
in his first year in a league was 58%. His pass completion percentage was 1.5% times better each year thereafter. Find his pass completion
percentage in his 12th year in the league.
Answers
The quarterback's pass completion percentage is 74.5%.
How to find the quarterback's pass completion percentage?To find the quarterback's pass completion percentage in his 12th year in the league
We can use the information given about his first year and the fact that his completion percentage improved by 1.5% each year.
Let's start by finding his completion percentage in his second year:
In his second year, his completion percentage was 58% + 1.5% = 59.5%.
We can continue this pattern to find his completion percentage in each subsequent year:
In his third year: 59.5% + 1.5% = 61%
In his fourth year: 61% + 1.5% = 62.5%
In his fifth year: 62.5% + 1.5% = 64%
In his sixth year: 64% + 1.5% = 65.5%
In his seventh year: 65.5% + 1.5% = 67%
In his eighth year: 67% + 1.5% = 68.5%
In his ninth year: 68.5% + 1.5% = 70%
In his tenth year: 70% + 1.5% = 71.5%
In his eleventh year: 71.5% + 1.5% = 73%
In his twelfth year: 73% + 1.5% = 74.5%
Therefore, the quarterback's pass completion percentage in his 12th year in the league is 74.5%.
Learn more about quarterback's pass
brainly.com/question/13777591
#SPJ11
What solid is formed when rotating a square about a horizontal or vertical axis through the center of the square?
(select) = cylinder, cube, sphere, square
does this solid have a square for a base?
yes or no
does this solid have a square for a cross-section?
yes or no
Answers
A cylinder is the solid shape that is created when square is rotated about a horizontal or vertical axis passing through its center. This solid does have a square for a base but does not have a square for a cross-section.
When a square is rotated about a horizontal or vertical axis passing through the center of the square, it creates a solid called a cylinder. A cylinder is characterized by its curved lateral surface and two circular bases at each end.
The base of the cylinder is formed by the square that was rotated. Hence, the base of the cylinder formed by rotating a square about a horizontal or vertical axis through its center is indeed a square.
However, when we consider a cross-section of the cylinder, it is not a square. The cross-section of a cylinder is a circle, regardless of the orientation of the axis of rotation.
As we move along the height of the cylinder, the cross-section remains consistent and is always circular. Therefore, the solid formed by rotating a square about a horizontal or vertical axis through its center has a square for a base but does not have a square for a cross-section.
Learn more about axis here:
brainly.com/question/2491015
#SPJ11
Find an equation in spherical coordinates for the surface represented by the rectangular equation. x² + y² + 2² - 3z = 0 P = 3 cos (0) X Need Help? Read It Watch It DETAILS LARCALC11 11.7.062. Convert the point from cylindrical coordinates to spherical coordinates. (-4,-3) (p, 0, 4) = Read It 9. [-/1 Points] Need Help? 11. [-/1 Points] DETAILS LARCALC11 11.7.079. Convert the rectangular equation to an equation in cylindrical coordinates and spherical coordinates. x² + y² + z² = 8 (a) Cylindrical coordinates (b) Spherical coordinates Need Help? Read It Watch It MY NOTES
Answers
The equation x² + y² + z² = 8 represents a surface in both cylindrical and spherical coordinates. In cylindrical coordinates, the equation remains the same. In spherical coordinates, the equation can be expressed as ρ² = 8, where ρ is the radial distance from the origin.
In cylindrical coordinates, the equation x² + y² + z² = 8 remains unchanged because the equation represents the sum of squares of the radial distance (ρ), azimuthal angle (θ), and the height (z) from the z-axis. Therefore, the equation in cylindrical coordinates remains x² + y² + z² = 8.
In spherical coordinates, we can express the equation by converting the Cartesian variables (x, y, z) into spherical variables (ρ, θ, φ). The conversion equations are:
x = ρ sin φ cos θ
y = ρ sin φ sin θ
z = ρ cos φ
Substituting these expressions into the equation x² + y² + z² = 8:
(ρ sin φ cos θ)² + (ρ sin φ sin θ)² + (ρ cos φ)² = 8
Simplifying this equation:
ρ² (sin² φ cos² θ + sin² φ sin² θ + cos² φ) = 8
Using the trigonometric identity sin² θ + cos² θ = 1, we have:
ρ² (sin² φ + cos² φ) = 8
Since sin² φ + cos² φ = 1, the equation further simplifies to:
ρ² = 8
Thus, in spherical coordinates, the surface represented by the equation x² + y² + z² = 8 can be expressed as ρ² = 8, where ρ is the radial distance from the origin.
Learn more about equation here: brainly.com/question/29657983
#SPJ11
Solve the equation for all solutions in the interval. Write each answer in radians.


Answers
We are given a problem regarding trigonometric identities and asked to resolve for theta.
\(4\sec \theta-\sqrt[]{3}=\sqrt[]{3}+7\sec \theta\)Recall that:
\(\sec \theta=\frac{1}{\cos \theta}\)Therefore, we have:
\(\begin{gathered} \frac{4}{\cos\theta}-\sqrt[]{3}=\sqrt[]{3}+\frac{7}{\cos\theta} \\ \text{ We add }\sqrt[]{3}\text{ and subtract }\frac{7}{\cos\theta}\text{ from both sides to get:} \\ \frac{4}{\cos\theta}-\frac{7}{\cos\theta}=2\sqrt[]{3} \\ -\frac{3}{\cos\theta}=2\sqrt[]{3} \\ \text{Multiply both sides by }\cos \theta\text{ and divide both sides by }2\sqrt[]{3}\text{ to get:} \\ \cos \theta=-\frac{3}{2\sqrt[]{3}}=-\frac{\sqrt[]{3}}{2} \\ \theta=\cos ^{-1}(-\frac{\sqrt[]{3}}{2})=150^o \\ \end{gathered}\)In radians, we have:
\(\frac{150\pi}{180}=\frac{5\pi}{6}\)What is the surface area of a cuboid?
Answers
As the cuboid has six rectangular faces, the total surface area of the cuboid is calculated as follows: Assume that, l, w, h be the length, width, and height of the cuboid respectively. Therefore, the total surface area of the cuboid is 2 (lh + lw+ hw) square units.
7. Assume that when you take a bath, you fill a tub to the halfway point. The portion that you fill measures 6 feet by 2 feet by 2.2 feet. When you take a shower, your use a shower head with a flow rate of 2.23 gallons per minutes and you typically spend 8 minutes in the shower. There are 7.5 gallons in one cubic foot. a. Calculate the cubic feet of water for the bath. b. Calculate the cubic feet of water for the shower. C. How many minutes do you need in the shower to use as much water as the bath?
Answers
The volume of water filled in the bath tub is 6 feet × 2 feet × 2.2 feet = 26.4 cubic feet. You need 11.83 minutes in the shower to use as much water as the bath.
The volume of water filled in the bath tub is 6 feet × 2 feet × 2.2 feet = 26.4 cubic feet.
The amount of water used in shower = flow rate × time = 2.23 gallons/minute × 8 minutes = 17.84 gallons
Let's convert gallons to cubic feet: 1 cubic foot = 7.5 gallons
17.84 gallons = 17.84/7.5 cubic feet = 2.378 cubic feet
The volume of water used in the shower is 2.378 cubic feet. The volume of water used for taking a bath is 26.4 cubic feet.
To calculate how many minutes one would need in the shower to use as much water as the bath, divide the volume of water used in taking a bath with the amount of water used per minute in the shower as shown:
26.4/2.23=11.83 min
Therefore, one needs 11.83 minutes in the shower to use as much water as the bath.
To know more about volume, visit:
https://brainly.com/question/1578538
#SPJ11