Paolo purchased a shirt at store A. He paid $19.50 for the shirt. Raoul purchased the same shirt at store B for $22.35.
How much money did Paolo save by purchasing the shirt at store A instead of at store B?
Answers
Answer:
2.85
Step-by-step explanation:
Reason 19.50 - 22.35 = 2.85
Related Questions
What are the roots of the polynomial equation x cubed minus 5 x 5 = 2 x squared minus 5? use a graphing calculator and a system of equations. round noninteger roots to the nearest hundredth.
Answers
The solution to the equation of the polynomial function x³-5x+5 = 2x²-5 is (c) –2.24, 2, 2.24.
What is Polynomial Equation?
A polynomial is an expression consisting of indeterminates and coefficients, that involves only the operations of addition, subtraction, multiplication, and non-negative integer exponentiation of variables.
Here, The function is given as:
x³-5x+5 = 2x²-5
Split the function.
So, we have:
y = x³-5x+5
y = 2x²-5
Using a graphing calculator, we have the x coordinate at the point o intersection of both equations to be
x = –2.24, 2, 2.24
Hence, the solution to the equation is (c) –2.24, 2, 2.24
Learn more about system of equations at:
brainly.com/question/14323743
#SPJ1
What is the equation of a line parallel to the line that passes through the
points (1, 8) and (3, 14) and has ay intercept of 9
Answers
Answer:
We can write the equation of a line parallel to a given line if we know a point on the line and an equation of the given line. y=2x+3 . Parallel lines have the same slope. The slope of the line with equation y=2x+3 is 2 .
Step-by-step explanation:
how many natural numbers have no more than 4 digits
Answers
There are 9,999 natural numbers that have no more than 4 digits.
To determine the number of natural numbers that have no more than 4 digits, we consider the range of numbers from 1 to 9,999.
The natural numbers with no more than 4 digits include all numbers from 1 to 9 (which form the single-digit numbers), all numbers from 10 to 99 (which form the two-digit numbers), all numbers from 100 to 999 (which form the three-digit numbers), and all numbers from 1,000 to 9,999 (which form the four-digit numbers).
To calculate the total count, we can add the number of single-digit numbers, two-digit numbers, three-digit numbers, and four-digit numbers:
Single-digit numbers: 9 (from 1 to 9)
Two-digit numbers: 90 (from 10 to 99)
Three-digit numbers: 900 (from 100 to 999)
Four-digit numbers: 9,000 (from 1,000 to 9,999)
Adding these counts together:
9 + 90 + 900 + 9,000 = 9,999
Therefore, there are 9,999 natural numbers that have no more than 4 digits.
To know more about natural numbers, refer here:
https://brainly.com/question/16978976
#SPJ4
5500 trees were planted on 1st october 2018 only 5060 trees were alive on 1st october 2019 it is assumed that the number of trees alive is given by N = ar where N is the number of trees still alive t years after October 1 2018 What is the value of a
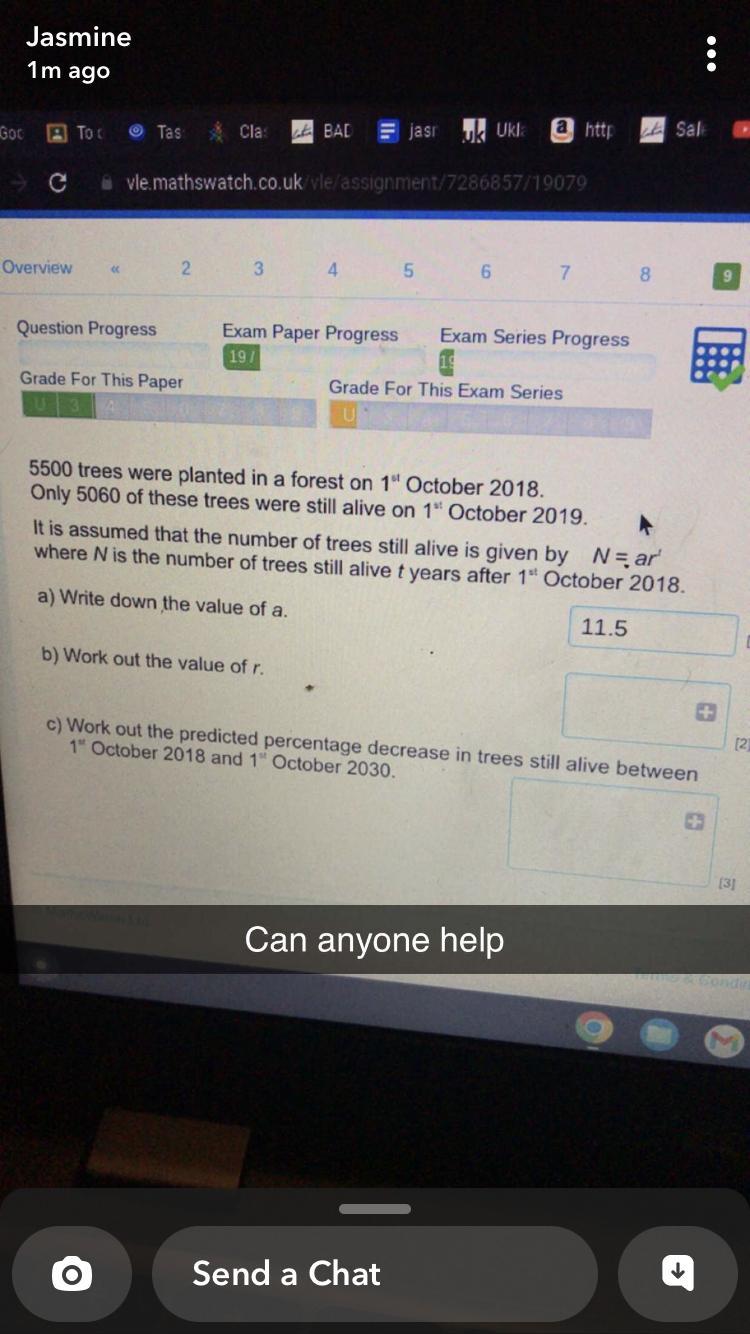
Answers
Considering the information about trees, The value of a is 5500
The value of r is calculated to be 0.92
In 1 October 2030 the number is 2022
How to find the value of aA mathematical function called an exponential function is employed frequently in everyday life. It is mostly used to compute investments, model populations, determine exponential decay or exponential growth, and so on.
Exponential function is a type of function of the form: f(x) = a(b)^x. It is made up of 3 main parts
a = the starting or initial value
b = the base function
x = the exponents
Considering the given problem, N = ar^t
the starting, a = 5500
the base, r =
the exponents = t
Solving for the base
N = ar^t
5500 = ar^t in 2018 t = 0
a = 5500
in 2019, t = 1
N = ar^t
5060 = 5500 * r
r = 5060/5500
r = 0.92
From 2018 to 2030 = 12 years, hence t = 12
N = 5500 * 0.92^12
N = 2,022.165132
N = 2022
Learn more about exponential function here:
https://brainly.com/question/29716012
#SPJ1
Seven seniors B, D, F, J, K, L and M are looking for positions after they graduate. The university has posted open positions for an accountant (a), consultant (c), editor (e), programmer (p), reporter (r), secretary (s), and teacher (t). Each of the seven students has applied for some of these positions: B:c,e D: a, c, p, s,t F: c,r J:c, e,r K: a, e, p, s L: e,r M: p, r, s, t - Page 3 of 3 Construct a graph representation of the problem and determine whether or not all seven students can be hired for the position they like.
Answers
A graph representation of the problem is shown in the image attached. The graph shows the seven seniors and the open positions posted by the university.
Each node in the graph represents a senior or a position. An edge connects a senior and a position if the senior has applied for that position. For instance, B has applied for positions c and e, so there are edges between node B and nodes c and e.
Similarly, there are edges between each senior and the positions they have applied for. The graph is bipartite since there are two sets of nodes, seniors and positions, and all edges connect a senior to a position (and vice versa). It is not possible to hire all seven students for the position they like since there are only four reporter positions available, but three students (F, J, and L) have applied for the reporter position. Therefore, at least one of these students will not be able to get the position they like.
Know more about graph representation here:
https://brainly.com/question/15710429
#SPJ11
ASAP PLEASEE The relationship between the number of pies-to-cakes chosen by middle school students as their favorite dessert is shown in the table.
Pie 36 42 60
Cake D 7 B
Total C A 70
What is the value of C in the table?
6
10
42
49
Answers
Answer: A) 6
Step-by-step explanation:
The ratio can be found by looking at the last column. If there are 60 pies and 70 items total, then the amount of pies would be 10.
This would make the ratio 6:1, or 6 pies for every 1 cake.
This can be confirmed by looking at the second column. If you treat the numbers like a fraction 42/7, you would once again get 6/1, as 42 divided by 7 is 6.
Daija is looking to fertilize her 24,000 square foot lawn. Super Lawn fertilizer costs $18. 49 and covers 6,000 square feet. Quick Fertilizer costs $23. 99 and covers 8,000 square feet.
Part A
Which fertilizer would be cheaper for Daija to purchase to fertilize her entire lawn? Show your work or explain your answer.
The cheapest fertilizer would be Super Lawn fertilizer because if you multiply the individual cost by her entire lawn and then divide it by the cost of one square feet, you will notice that she pays less with the Super Lawn.
Part B:
Daija has a 15% off coupon on the cheaper fertilizer. Excluding sales tax, what is the new cost of the fertilizer? Round to the nearest cent.
Answers
The new cost of the fertilizer after applying the coupon is $20.39 (excluding sales tax).
Part A:
To determine which fertilizer would be cheaper for Daija to purchase, we need to calculate the cost per square foot for each fertilizer.
Super Lawn fertilizer costs $18.49 and covers 6,000 square feet. Cost per square foot for Super Lawn fertilizer = $18.49 / 6,000 = $0.00308 per square foot.
Quick Fertilizer costs $23.99 and covers 8,000 square feet. Cost per square foot for Quick Fertilizer = $23.99 / 8,000 = $0.00299 per square foot.
Comparing the cost per square foot, we can see that Quick Fertilizer is cheaper. Therefore, Daija should purchase Quick Fertilizer to fertilize her entire lawn.
Part B:
Daija has a 15% off coupon on the cheaper fertilizer, which is Quick Fertilizer. To calculate the new cost of the fertilizer after applying the coupon, we need to subtract 15% of the original cost from the original cost.
Original cost of Quick Fertilizer = $23.99
15% of $23.99 = $23.99 * 0.15 = $3.599
New cost of Quick Fertilizer = $23.99 - $3.599 = $20.391
Rounded to the nearest cent, the new cost of the fertilizer after applying the coupon is $20.39 (excluding sales tax).
To know more about cost click here
brainly.com/question/19075809
#SPJ11
In a random sample of 190 people, 151 said that they watched educational television. Find the 90% confidence interval of the true proportion of people who watched educational television. Round intermediate answers to at least five decimal places. Round your final answers to at least three decimal places.
Answers
Answer:
(0.7465 , 0.8429 )
Step-by-step explanation:
Confidence Level - "P" values
90% 1.645
Confidence Interval - "P" values
(0.7465 , 0.8429 )
I need help solving |-5y+9|= 14
Answers
Answer:
-5 turns into 5 and the y is probably 1, so 5+9 is equal to 14.
Step-by-step explanation:
determine whether the relation r on the set of all integers is reflexive, symmetric, antisymmetric, and/or transitive, where (x,y) in r if and only if: x = y − 1 or y = x − 1.
Answers
The relation R is symmetric and antisymmetric, but not reflexive or transitive.
Let's examine each property of the relation R separately:
Reflexive: A relation R is reflexive if every element in the set is related to itself. In this case, we have (x, x-1) or (x-1, x) for any integer x. Therefore, the relation is not reflexive since x is not related to itself.
Symmetric: A relation R is symmetric if for any pair of elements x and y in the set, (x,y) being in R implies that (y,x) is also in R. In this case, we have (x, y-1) or (y, x-1) for any integers x and y. It is clear that if (x, y-1) is in R, then (y, x-1) is also in R, and vice versa. Therefore, the relation is symmetric.
Antisymmetric: A relation R is antisymmetric if for any distinct elements x and y in the set, if (x,y) is in R, then (y,x) cannot also be in R. In this case, if we have (x, y-1) and (y, x-1), then x = y-1 and y = x-1. This implies that x = y, which contradicts our assumption that x and y are distinct. Therefore, the relation is antisymmetric.
Transitive: A relation R is transitive if for any elements x, y, and z in the set, if (x,y) and (y,z) are in R, then (x,z) is also in R. In this case, we have (x, y-1) and (y, z-1) for any integers x, y, and z. If we add these two relations, we get (x, z-2).
However, this does not satisfy the original relation, which requires that (x, z-1) be in R. Therefore, the relation is not transitive.
In summary, the relation R is symmetric and antisymmetric, but not reflexive or transitive.
Click the below link, to learn more about the relation r of all integers:
https://brainly.com/question/30881382
#SPJ11
Help me solve this pleasee

Answers
First before replacing the variable let us rephrase the equation.
s = 1/2(v + u)t, can also be written as,
t/2(u + v)
Now replacing the variables,
5/2(6 + 20) = s
2.5 * 26 = s
hence,
s = 65m
Answer:
B. 65 mStep-by-step explanation:
\(s = \frac{1}{2} (u + v)t \\ s = \frac{1}{2} (6 + 20)5 \\ s = \frac{1}{2} \times 26 \times 5 \\ s = 13 \times 5 \\ s = 65 \\ \)
Prior to an election, 6,504 people vote in the advance polls for a riding. On election day, thepolling stations for that riding record an average of 407 voters per hour. How long were thepolls open on election day, if a total of 10,167 people voted in that riding?
**USE LET STATEMENTS, AND THEREFORE STATEMENTS**
Answers
Answer:
The polls were open for 9 hours on election day.
Step-by-step explanation:
10167 - 6504 = 3663
3663 / 407 = 9
If the observations have weights of 2, 3 and 1 respectively, solve these equations for the most probable values of A and B using weighted least squares method. Solve the problem using both algebraic approach and matrices and compare your results.
A+2B=10.50+V1
2A-3B=5.55+V2
2A-B=-10.50+V3
Answers
The results obtained using the algebraic approach and the matrix approach should be the same. Both methods are mathematically equivalent and provide the most probable values of A and B that minimize the sum of squared weighted residuals.
To solve the system of equations using the weighted least squares method, we need to minimize the sum of the squared weighted residuals. Let's solve the problem using both the algebraic approach and matrices.
Algebraic Approach:
We have the following equations:
A + 2B = 10.50 + V1 ... (1)
2A - 3B = 5.55 + V2 ... (2)
2A - B = -10.50 + V3 ... (3)
To minimize the sum of squared weighted residuals, we square each equation and multiply them by their respective weights:
\(2^2 * (A + 2B - 10.50 - V1)^2\)
\(3^2 * (2A - 3B - 5.55 - V2)^2\\1^2 * (2A - B + 10.50 + V3)^2\)
Expanding and simplifying these equations, we get:
\(4(A^2 + 4B^2 + 10.50^2 + V1^2 + 2AB - 21A - 42B + 21V1)\\9(4A^2 + 9B^2 + 5.55^2 + V2^2 + 12AB - 33A + 16.65B - 11.1V2)\\(A^2 + B^2 + 10.50^2 + V3^2 + 2AB + 21A - 21B + 21V3)\\\)
Now, let's sum up these equations:
\(4(A^2 + 4B^2 + 10.50^2 + V1^2 + 2AB - 21A - 42B + 21V1) +\\9(4A^2 + 9B^2 + 5.55^2 + V2^2 + 12AB - 33A + 16.65B - 11.1V2) +\\(A^2 + B^2 + 10.50^2 + V3^2 + 2AB + 21A - 21B + 21V3)\int\limits^a_b {x} \, dx\)
Simplifying further, we obtain:
\(14A^2 + 31B^2 + 1113 + 14V1^2 + 33V2^2 + 14V3^2 + 14AB - 231A - 246B + 21V1 - 11.1V2 + 21V3 = 0\)
Now, we have a single equation with two unknowns, A and B. We can use various methods, such as substitution or elimination, to solve for A and B. Once the values of A and B are determined, we can substitute them back into the original equations to find the most probable values of A and B.
Matrix Approach:
We can rewrite the system of equations in matrix form as follows:
| 1 2 | | A | | 10.50 + V1 |
| 2 -3 | | B | = | 5.55 + V2 |
| 2 -1 | | -10.50 + V3 |
Let's denote the coefficient matrix as X, the variable matrix as Y, and the constant matrix as Z. Then the equation becomes:
X * Y = Z
To solve for Y, we can multiply both sides of the equation by the inverse of X:
X^(-1) * (X * Y) = X^(-1) * Z
Y = X^(-1) * Z
By calculating the inverse of X and multiplying it by Z, we can find the values of A and B.
Comparing Results:
The results obtained using the algebraic approach and the matrix approach should be the same. Both methods are mathematically equivalent and provide the most probable values of A and B that minimize the sum of squared weighted residuals.
For more such questions on matrix visit:
https://brainly.com/question/1279486
#SPJ8
HELP PLEASE!! ALSO IF U CAN PLEASE ANSWER MY RECENT QUESTIONS OF TODAY IF UR GENEROUS THANKS BAES

Answers
Answer:b
Step-by-step explanation:
just took the quiz
Use the Pythagorean equation of
A^2 + B^2 = C^2
After 4 minutes of reading, Aaron was on page 14 of his book. After 8 minutes he was on page 20. Which equation models the page number, y in terms of minutes x?
A. y=-8x+1.5
B. y=1.5x+8
C. y=8x+1.5
D. y=-1.5x+8
Answers
Given:
After 4 minutes of reading, Aaron was on page 14 of his book.
After 8 minutes he was on page 20.
To find:
The equation that models the page number, y in terms of minutes x.
Step-by-step explanation:
Let y be the page number after x minutes of reading.
After 4 minutes of reading, Aaron was on page 14 of his book. So, the line must be passes through (4,14).
After 8 minutes he was on page 20. So, the line must be passes through (8,20).
The equation of line which passes through two points is
\(y-y_1=\dfrac{y_2-y_1}{x_2-x_1}(x-x_1)\)
The required line passes through (4,14) and (8,20), so the equation is
\(y-14=\dfrac{20-14}{8-4}(x-4)\)
\(y-14=\dfrac{6}{4}(x-4)\)
\(y-14=1.5(x-4)\)
\(y-14=1.5x-6\)
Add 14 on both sides.
\(y-14+14=1.5x-6+14\)
\(y=1.5x+8\)
Therefore, the correct option is B.
X=
2 Michael bakes a soft pretzel and a loaf of bread. Use the system of equations to
find c, the amount of flour, in cups, needed for the soft pretzel, and b, the amount
of flour, in cups, needed for the loaf of bread. Show your work.
b = 24c
5
16+ 4c = 2/
SOLUTION
Answers
The value of b is 3.
The value of c is 1/8.
What is an equation?An equation is a mathematical statement that is made up of two expressions connected by an equal sign.
Example:
2x + 5 = 9 is an equation.
We have,
Two equations given are:
b = 24c ____(1)
(1/4)b + 4c = 5/4 _____(2)
Putting (1) in (2) we get,
(1/4)24c + 4c = 5/4
6c + 4c = 5/4
10c = 5/4
c = 5/40
c = 1/8
Putting c = 1/8 in (1) we get,
b = 24/8
b = 3
Thus,
b = 3.
c = 1/8.
Learn more about equations here:
https://brainly.com/question/17194269
#SPJ1
Sydney has a quarters and y dimes, having no less than 18 coins worth a maximum of $3.60 combined. A minimum of 4 of the coins are quarters and at least 16 of the coins are dimes. Solve this system of inequalities graphically and determine one possible solution.
HELP ME ASAP PLEASE!!!
Answers
Step-by-step explanation:
x + y = 18 We have at least 4 quarters
0.25x + 0.1y = 3.6
If we graph both equations, the point of intersection will give us our answer.
In this case, the lines intersect at the point (12, 6) which means I have 12 quarters and 6 dimes. This solution is correct as it also satisfies the condition of having at least 4 quarters.
(got this from another website, maybe it's wrong..
Wishing you the best!! )
The quadrilateral is a trapezoid. What is the value of x?
A. 4
B. 5
C. 48
D. 25
Answers
If the quadrilateral is a trapezoid , then the value of x is = (b) 5 .
We know that the Midsegment of a trapezoid is parallel to each of the base and it's length is one half the sum of the lengths of the bases.
From the figure , we can observe that ⇒ side lengths are 21 units, 27 units , and the sides are parallel to each other.
From the given diagram of the trapezoid , the below expression is true:
that means : ⇒ 5x-1 = (21 + 27)/2 ;
⇒ 2(5x - 1) = 21 + 27 ;
⇒ 10x = 48 + 2 ;
⇒ 10x = 50
On Divide both sides by 10 ;
we have ;
⇒ x = 50/10 ;
⇒ x = 5 .
Therefore , for the quadrilateral the value of x is = 5 .
Learn more about Trapezoid here
https://brainly.com/question/8643562
#SPJ4
The given question is incomplete , the complete question is
The quadrilateral in the below figure is a trapezoid. What is the value of x ?
(a) 4
(b) 5
(c) 48
(d) 25

A group of 125 teenagers were asked which of the following activities they would most likely choose to spend their free time doing: reading a book, watching television, playing video games, or listening to music. The results are displayed in the circle graph below.
What is the difference in percent between those who chose reading a book and those who chose to listen to music?
a. 16%
b. 8%
c. 12%
d. 4%

Answers
Answer:
12%
Step-by-step explanation:
Read a book = 16%
Listen to music = 28%
We can read the question in different ways:
1. The simple difference between the two is 12%
2. Out of the sample, the two groups include:
15 chose books
35 chose music
Within this sample of 50 teenagers,
(15/50) or 30% chose books, and
(35/50) or 70% chose music
That makes a difference of 40%
I would chose the first interpretation, 12% [Especially since 40% is not an option.]
A triangle PQR is right angled at R, with PQ=80cm and R=60cm. find QR?
Step by step PLS PYTHAGORUS THEOREM
Answers
Answer:
Solution given:
A triangle PQR is right angled at R, with hypotenuse{h}PQ=80cm
and
base[b]PR=60cm.
perpendicular [P]= QR
by using Pythagoras law
h²=p²+b²
80²=QR²+60²
QR²=80²-60²
QR=\(\sqrt{2800}\)
QR=20\(\sqrt{7}\)=52.9=53cm
QR=53cm.
Consider a spring-mass system, with k=4000 N/m and m= 10 kg, subject to a harmonic force F(t) = 400 cos 30t N. Find the total response of the system under the initial conditions of xo = 0.1 m and to 10 m/s.
Answers
The equation that shows the total response of the system under the initial conditions of xo = 0.1 m and to 10 m/s is:
x(t) = (-1/5) * cos(30t) + 0.1 * cos(20t) + 0.5 * sin(20t).
How to solve Differential Equations?The equation that describes the motion of the system is given by:
m * x''(t) + k * x(t) = F(t),
where:
m is the mass
x(t) is the displacement of the mass from the equilibrium position
x''(t) is the second derivative of x(t) with respect to time
k is the spring constant
F(t) is the external force.
Given that k = 4000 N/m, m = 10 kg, and F(t) = 400 cos(30t) N, we can substitute these values into the differential equation:
10 * x''(t) + 4000 * x(t) = 400 cos(30t).
Using the method of undetermined coefficients, we assume the solution has the form:
x(t) = A * cos(30t) + B * sin(30t) + C
where A, B, and C are constants to be determined.
Taking the derivatives, we have:
x''(t) = -900 A * cos(30t) - 900 B * sin(30t),
Substituting these into the differential equation, we get:
-9000 A * cos(30t) - 9000 B * sin(30t) + 4000 (A * cos(30t) + B * sin(30t) + C) = 400 cos(30t).
Equating the coefficients of cos(30t), sin(30t), and the constant terms separately, we get the following equations:
-9000 A + 4000 A = 400,
-9000 B + 4000 B = 0,
4000 C = 0.
Solving these equations, we find A = -1/5, B = 0, and C = 0.
Thus, the particular solution to the differential equation is:
x_p(t) = (-1/5) * cos(30t).
Now, we need to find the general solution to the homogeneous equation:
10 * x''(t) + 4000 * x(t) = 0.
The characteristic equation is:
10 * r² + 4000 = 0,
r² = -400,
which has complex roots r₁ = 20i and r₂ = -20i.
The general solution to the homogeneous equation is:
x_h(t) = A * cos(20t) + B * sin(20t),
where A and B are constants to be determined.
To find the values of A and B, we apply the initial conditions:
x(0) = x₀ = 0.1 m,
x'(0) = v₀ = 10 m/s.
Substituting t = 0 into the general solution and its derivative, we get:
x_h(0) = A = x₀ = 0.1,
x_h'(0) = 20B = v₀ = 10,
B = 0.5.
Therefore, the general solution to the differential equation is:
x_h(t) = 0.1 * cos(20t) + 0.5 * sin(20t).
Finally, the total response of the system is the sum of the particular and homogeneous solutions:
x(t) = x_p(t) + x_h(t),
x(t) = (-1/5) * cos(30t) + 0.1 * cos(20t) + 0.5 * sin(20t).
Read more about Differential Equations at; https://brainly.com/question/1164377
#SPJ1
For 15-20, solve each equation. Identifyany extraneous roots. I’ve completed most of the problem, I just am struggling to find ‘x’

Answers
ANSWER
Solutions: x = -6, x = 2i, and x = -2i
EXPLANATION
To solve this equation, first, we have to raise both sides of the equation to the exponent 3,
\(\begin{gathered} \left({(8x-16)^{1\/3})^3}\right.=(x+2)^3 \\ \\ 8x-16=(x+2)^3 \end{gathered}\)Now, we have to expand the binomial cubed using the cube of a binomial rule,
\((a+b)^3=a^3+3a^2b+3ab^2+b^3\)So we have,
\((x+2)^3=x^3+3x^2\cdot2+3x\cdot2^2+2^3=x^3+6x^2+12x+8\)So the equation is,
\(8x-16=x^3+6x^2+12x+8\)Subtract 8x from both sides of the equation, and also add 16 to both sides,
\(\begin{gathered} 8x-8x-16+16=x^3+6x^2+12x-8x+8+16 \\ \\ x^3+6x^2+4x+24=0 \end{gathered}\)So, we have to find the zeros of this equation.
First, assuming at least one root is an integer, write the possible values. Since the constant is 24, the possible roots are factors of 24:
\(24:\pm2,\operatorname{\pm}3,\operatorname{\pm}4,\operatorname{\pm}6,\operatorname{\pm}8,\operatorname{\pm}12\)Now, let's test these values in the equation,
\(\begin{gathered} f(2)=64;f(-2)=32 \\ f(3)=117;f(-3)=39 \\ ... \\ f(-6)=0 \\ ... \end{gathered}\)*Note: I have not tested all the possible values in this answer to make the explanation shorter.
Now, we know that x = -6 is a zero, so (x + 6) is a factor. To find the quadratic factor, we can divide the 3rd-degree polynomial by the factor (x + 6):
\((x^3+6x^2+4x+24)\div(x+6)=x^2+4\)The zeros of the resulting factor are not real,
\(\begin{gathered} x^2+4=0 \\ x=\sqrt{-4}=\pm2i \end{gathered}\)Hence, the solutions of this equation are x = -6, x = 2i, and x = -2i.
Help please my moms going to kill me if I don’t get this right

Answers
Answer:
\(x=-\frac{41}{6}\)
Step-by-step explanation:
Pay attention to the two tick marks. This indicates that those sides are congruent to each other and so will the angles on the bottom and top. Therefore, we can set up the equation \(137+2(-3x+1)=180\) and solve for x:
\(137+2(-3x+1)=180\)
\(137+(-6x+2)=180\)
\(137-6x+2=180\)
\(139-6x=180\)
\(-6x=41\)
\(x=-\frac{41}{6}\)
juliet rented a car for one day from a company that charges $80 per day plus $0.15 per mile driven. if she was charged a total of $98 for the rental and mileage, for how many miles of driving w
Answers
Juliet was charged $18 for driving 120 miles.
Given,
The rent of car per day = $80
The charge for per miles driven = $0.15
Juliet was charged a total of $98 for the rental and mileage.
We have to find the total miles of driving;
Here,
Charge for miles driven = Total charge - Rent of car for a day
Charge for miles driven = 98 - 80
Charge for miles driven = $18
Now,
Total miles driven = Charge for miles driven / Charge for one mile
Total miles driven = 18/0.15
Total miles driven = 120
That is,
Juliet was charged $18 for 120 miles of driving.
Learn more about charge for driving here;
https://brainly.com/question/13250700
#SPJ4
Set up an amortization schedule for a $19,000 loan to be repaid in equal installments at the end of each of the next 3 years. The interest rate is 8% compounded annually. What percentage of the payment represents interest and what percentage represents principal for each of the 3 years? Why do these percentages change over time?
Answers
The problem involves setting up an amortization schedule for a $19,000 loan to be repaid in equal installments at the end of each of the next 3 years.
The interest rate is 8% compounded annually. The task is to determine the percentage of the payment that represents interest and principal for each year and explain why these percentages change over time.
To set up an amortization schedule, we need to calculate the equal installment payment for each year. The loan amount of $19,000 is divided by 3 years to determine the annual payment. In this case, the annual payment would be $6,333.33.
In the first year, the interest portion of the payment is calculated based on the outstanding loan balance, which is $19,000. The interest is 8% of $19,000, which is $1,520. The principal portion of the payment is the difference between the annual payment and the interest, which is $6,333.33 - $1,520 = $4,813.33.
For the second year, the interest portion is calculated based on the remaining loan balance after the first year's payment. The interest is 8% of the remaining balance, which is $19,000 - $4,813.33 = $14,186.67. The principal portion is the difference between the annual payment and the interest, which is $6,333.33 - $14,186.67 = -$7,853.34. Since the principal portion is negative, it means the loan will be fully paid off in the second year.
In the third year, there is no outstanding loan balance, so both the interest and principal portions of the payment will be zero.
The percentages of interest and principal change over time because the interest is calculated based on the remaining loan balance, which decreases with each payment. As the loan balance decreases, the interest portion becomes smaller, and the principal portion becomes larger. Therefore, the interest percentage decreases, while the principal percentage increases over the repayment period.
To learn more about percentage click here:
brainly.com/question/32197511
#SPJ11
Find the value of x that makes ABCD a parallelogram?
answers
a.) x=30
b.) x=20
c.) x=40
d.) x=60

Answers
Answer:
D) x=60
The choose
Step-by-step explanation:
360 =70+70+50+50+2x
360=240+2x
360-240=2x
120=2x
x=120/2
x=60
Which value of x makes the equation 2(x-9)-2x=-3(3+7) true?
Answers
Answer:
No solution
Step-by-step explanation:
a rotating sprinkler can reach up to 14 feet through a 300 degree angle. find the total area covered by the sprinkler in one sweep. round to the nearest tenth. What is the area of the lawn, to the nearest square foot, that receives water from this sprinkler?
Answers
In one sweep, the area covered by the sprinkler is 77.19 sq ft (approx). The area of the lawn, to the nearest square foot, that receives water from this sprinkler is 616 sq ft (approx).
We know that a rotating sprinkler can reach up to 14 feet through a 300-degree angle. Area covered by the sprinkler in one sweep = area of the sector whose radius = 14 feet and angle = 300°Area of sector = (θ / 360) × πr²Where θ = 300°, r = 14 ftArea of sector = (300/360)× π(14)²= 77.19 sq ft (approx) Therefore, the area covered by the sprinkler in one sweep is 77.19 sq ft (approx).
We need to find the total area of the lawn that receives water from this sprinkler. The sprinkler rotates 360 degrees, so it will cover a full circle whose radius is 14 feet. Area of a circle = πr²= π(14)²= 615.752 sq ft (approx) Therefore, the area of the lawn, to the nearest square foot, that receives water from this sprinkler is 616 sq ft (approx).
To know more about area visit:-
https://brainly.com/question/1631786
#SPJ11
Write the point-slope form of the given line that passes through the points (0, -3) and (4, 1). Identify (x1, y1) as (0, -3). Include your work in your final answer. Type your answer in the box provided or use the upload option to submit your solution.
Answers
Answer:
X1=0
Y1=-3
X2=4
Y2=1
Slope=(y2-y1)/(x2-x1)
Slope=(1-(-3))/(4-0)
Slope=4/4
Slope=1
Step-by-step explanation:
Mary, Katherine, and Alex share the bill at a restaurant after a meal. Mary pays for of the bill, Katherine pays for of the bill, and Alex
pays for the rest. What is the ratio of Mary's share to Katherine's share to Alex's share?
Answers
The ratio of Mary's share to Katherine's share to Alex's share is 5:4:1, which means Mary pays 5/10 of the bill, Katherine pays 4/10 of the bill, and Alex pays 1/10 of the bill.
To find the ratio, we can write their contribution as a fraction of the total parts and then solve the fractions then they'll have the same denominator.
So, Mary's share is 5/10, Katherine's share is 4/10, and Alex's share is 1/10.
To convert this as a ratio, we write 5:4:1, where each number represents the number of parts each person pays, and the colon separates each person's contribution.
Therefore, the ratio of Mary's share to Katherine's share to Alex's share is 5:4:1
To learn more about ratios:
https://brainly.com/question/12024093
#SPJ4