The mean lifespan is 71.45 years, and the standard deviation is 12.35 years. President Ronald Reagan lived to be 93 years old. Calculate and interpret his z-score
Answers
Answer:
The raw score of President Ronald Reagan is 1.745 which means that the President was older than approximately 96% of the population
Step-by-step explanation:
The z-score which is the standard score provides an indication the magnitude of the extent of a data point from the mean. It is calculated by measuring the number of standard deviations a data point is higher than or less than the mean.
The z-score, is given by the relation;
\(z = \dfrac{x - \mu}{\sigma}\)
Where;
x = The data point value
μ = The mean
σ = The standard deviation
Given that we have;
The mean lifespan = 71.45 years
The standard deviation = 12.35 years
We can find the raw score of President Ronald Reagan's age of 93 years as follows;
\(z = \dfrac{93 - 71.45}{12.35} \approx 1.745\)
The raw score of President Ronald Reagan is 1.745 which means that (by looking for the p value online) , the President was older than (1 - 0.040501) × 100 percent or approximately 96% of the population.
Related Questions
MA.912.FL.3.2: Solve real-world problems involving simple, compound and continuously compounded interest.
1. Earl opens a certificate of deposit with $1,500 that pays 2.75% compounded daily.
Part A: Write an equation to model this situation.
Part B. How much money will be in the account after 1 year?
Part C. How much money will be in the account after 5 years?
Answers
Part A: The formula for the future value of an investment with compound interest is given by:
A = P(1 + r/n)^(nt)
Where: A = the future value of the investment P = the principal investment amount r = the annual interest rate (as a decimal) n = the number of times the interest is compounded per year t = time in years
For this situation, P = $1,500 r = 2.75% = 0.0275 (since the interest rate is given as an annual rate, we need to divide it by 100 to convert it to a decimal) n = 365 (since interest is compounded daily) t = 1 (since we are looking for the value after one year)
Therefore, the equation to model this situation is:
A = 1500(1 + 0.0275/365)^(365*1)
Part B: To find the value of the account after one year, we can simply substitute t=1 into the equation:
A = 1500(1 + 0.0275/365)^(365*1) = $1,543.21
Therefore, the amount of money in the account after 1 year is $1,543.21.
Part C: To find the value of the account after 5 years, we need to substitute t=5 into the equation:
A = 1500(1 + 0.0275/365)^(365*5) = $1,805.59
Therefore, the amount of money in the account after 5 years is $1,805.59.
how many liters of a 25 % 25%, percent saline solution must be added to 3 33 liters of a 10 % 10, percent saline solution to obtain a 15 % 15, percent saline solution?'
Answers
Answer:
Here, x represents the amount (in liters) of the 25% saline solution to be added.
We can see that the 25% saline solution needs to be mixed with the 10% saline solution to obtain a mixture that is 15% saline. The ratio of the volumes of the 25% and 10% solutions can be found by subtracting the concentrations of the two solutions and dividing by the difference between the desired concentration and the concentration of the 10% solution:
x / (3.33 - x) = (15 - 10) / (25 - 10) = 5/15 = 1/3
Multiplying both sides by 3.33 - x, we get:
x = (1/3) (3.33 - x)
Multiplying both sides by 3, we get:
3x = 3.33 - x
Solving for x, we get:
x = 0.833 liters
Therefore, 0.833 liters of the 25% saline solution must be added to 3.33 liters of the 10% saline solution to obtain 4.163 liters of a 15% saline solution.
Step-by-step explanation:
Distributive Property to find (z-5)(z+3)
Answers
Answer:
z×(-5+3)then you complete the sum and that is your answer
Step-by-step explanation:
hope it helps you
Emily invested $810 in an account paying an interest rate of
Answers
Answer:
complete this
Step-by-step explanation:
yeah do it
Please help I need it I’ll give brainly please

Answers
PLZ ANSWER THESE U DONT HAVE TO PUT A EXPLANATION





Answers
Answer:
I believe it is the last choice.
Step-by-step explanation:
A baker made 27 blueberry muffins on Monday. What percent of the total number of muffins were blueberry if the baker made 90 muffins?
Answers
Answer: 0.3 or 30%
27/90 is 0.3
So therefore put into real perspective your answer is 30 percent
answerrrrrr plssss ill giveee brainliesttttt

Answers
\(m\angle E=\sin \dfrac{\sqrt{10}}{2\sqrt5}=\sin \dfrac{\sqrt2}{2}=45^{\circ}\)
For a project in his geometry class tom uses a mirror on the ground to measure the height of a school football goal post. he walks a distance of 12.65 m from his school then places a mirror flat on the ground marked with an x at the center. he then walks 6.3 more meters past a mirror so that when he turns around and looks down at the mirror he can see the top of the goalpost clearly marked by an x. his partner measures the distance from his eyes to the ground to be 1.45 m how tall is a goal post round your answer to the nearest hundredth of a meter
Answers
The height of the school football goal post is approximately 0.909 meters or 0.91 meters when rounded to the nearest hundredth which is obtained by using equation.
To determine the height of the goal post, Tom used the concept of similar triangles. When Tom stood 12.65 meters away from the mirror on the ground, he marked the center of the mirror with an "x." He then continued walking an additional 6.3 meters past the mirror. By turning around and looking down at the mirror, he could see the top of the goal post, also marked with an "x."
The key to solving this problem lies in the similarity of the triangles formed. The height of the goal post can be represented as 'h,' the distance between the mirror and Tom's eyes as 'd,' and the distance between Tom and the mirror as 'x.'
Using similar triangles, we can set up the following proportion:
h / (d - x) = x / d
Given that Tom's partner measured the distance from Tom's eyes to the ground as 1.45 meters, we substitute 'd' with 1.45 meters. Rearranging the equation, we can solve for 'h':
h = (x * 1.45) / (d - x)
Plugging in the values, we find:
h = (6.3 * 1.45) / (12.65 + 6.3) ≈ 0.909 meters
Therefore, the height of the school football goal post is approximately 0.909 meters or 0.91 meters when rounded to the nearest hundredth.
Learn more about equation here:
https://brainly.com/question/29174899
#SPJ11
evaluate: 3 /7 + ( −11 /4 ) + 16 /5 − ( −18 /7 )
Answers
Answer:
This is hard
Step-by-step explanation:
I'm so sorry I can't do it
Answer:
\(\frac{69}{20}\)
Step-by-step explanation:
\(\frac{3}{7} -\frac{11}{4} +\frac{16}{5} +\frac{18}{7}\)
= \(\frac{3}{7} +\frac{18}{7}-\frac{11}{4} +\frac{16}{5}\)
= \(\frac{21}{7} -\frac{11}{4} +\frac{16}{5}\) As both denominators have 7 you can add their numerators
=\(\frac{21}{7} -(-\frac{9}{20})\) L.C.M
=\(\frac{21}{7} +\frac{9}{20}\) L.C.M
=\(\frac{69}{20}\)
For a criminal trial, 8 active and 4 alternate jurors are selected. Two of the alternate jurors are male and two are female. During the trial, two of the active jurors are dismissed. The judge decides to randomly select two replacement jurors from the 4 available alternates. What is the probability that both jurors selected are female? 1/12 1/6 1/2 1/4
Answers
The probability that both jurors selected are female is 1/6. To calculate the probability that both jurors selected are female,.
We need to determine the number of favorable outcomes (two female jurors selected) divided by the total number of possible outcomes.
In this scenario, there are two female alternate jurors available out of a total of four alternates. Since we need to select two jurors, we can use combinations to calculate the number of possible outcomes.
The number of possible outcomes is given by selecting 2 jurors out of 4, which can be calculated as:
C(4, 2) = 4! / (2! * (4-2)!) = 6
Therefore, there are 6 possible outcomes.
Out of these possible outcomes, we are interested in the favorable outcome where both selected jurors are female. Since there are two female alternate jurors available, we can calculate the number of favorable outcomes by selecting 2 female jurors out of 2, which is:
C(2, 2) = 2! / (2! * (2-2)!) = 1
Therefore, there is 1 favorable outcome.
Now, we can calculate the probability:
Probability = Number of favorable outcomes / Number of possible outcomes
= 1 / 6
= 1/6
Thus, the probability that both jurors selected are female is 1/6.
Learn more about probability here:
https://brainly.com/question/32117953
#SPJ11
Find the equation of the line that passes through (4,4) and is parallel to y = 3 x + 4. Leave your answer in the form y = m x + c.
Answers
The equation of the line that passes through (4, 4) & parallel to y = 3x + 4 is y = 3x - 8 .
Slope intercept form:
The equation of line in slope intercept form is,
y = mx + c
Where m is slope of line and c is y-intercept.
Equation of line given that,
y = 3x + 4
So that, slope of line is 3.
We have to find the equation of the line that passes through (4,4) and is parallel to given lines.
Since, slope of all parallel lines are same.
Equation of required line is,
y = mx + c
Substitute point (4,4) in above line.
4 = 12 + c
c = 4 - 12
c = -8
So that, equation of line become,
y = 3x - 8 .
Learn more about the equation of line here:
brainly.com/question/18831322
#SPJ4
you put $250 into an account at the end of each year for 5 years. at the end of the 5th year the account was worth $1,750. what rate of return did you earn?
Answers
12.03% is the approximate amount rate of return earned.
Determining the rate of return on an amount investedWe can use the formula for the future value of an annuity to solve this problem. The formula is:
FV = P * ((1 + r)^n - 1) / r
where FV is the future value of the annuity, P is the payment (in this case, $250), r is the annual interest rate, and n is the number of years.
Using the information given in the problem, we know that:
P = $250
n = 5
FV = $1,750
Substituting these values into the formula, we get:
$1,750 = $250 * ((1 + r)^5 - 1) / r
Multiplying both sides by r and dividing both sides by $250, we get:
7 = ((1 + r)^5 - 1) / r
Multiplying both sides by r, we get:
7r = (1 + r)^5 - 1
Expanding the right side using the binomial theorem, we get:
7r = 1 + 5r + 10r^2 + 10r^3 + 5r^4 + r^5 - 1
Simplifying and rearranging, we get:
r^5 + 5r^4 + 10r^3 + 10r^2 - 7r = 0
We can solve this equation numerically using a calculator or a computer. One way to do this is to use the Newton-Raphson method, which is an iterative method that starts with an initial guess and refines it until it converges to a solution. Using this method with an initial guess of r = 0.1, we get:
r ≈ 0.1203
So the annual interest rate that you earned on the account is approximately 12.03%.
Learn more on future value here: https://brainly.com/question/24703884
#SPJ1
By looking to the top picture
what is the answer for my question
help asap please :)

Answers
Answer:
B and E
Step-by-step explanation:
Fit's, they multiplied both sides by 4/3 instead of 3/4. Then they divided the answer by 3 instead of taking the cube root of both sides.
If A = 5 and B = 3, what will be displayed when code corresponding to the following pseudocode is run? (In the answer options, new lines are separated by commas.)
Do
Write A^2
Set A = A - 1
While A >= B
Answers
The output when the given pseudocode is executed with A = 5 and B = 3 will be "25, 16, 9, 4, 1".
The given pseudocode includes a loop that iterates as long as A is greater than or equal to B. In each iteration, the square of A is displayed, and A is decremented by 1. We are asked to determine the output when A is initially 5 and B is 3.
Step 1: Initialization
A is set to 5 and B is set to 3.
Step 2: Iteration 1
Since A (5) is greater than or equal to B (3), the loop executes.
The square of A (5²) is displayed, resulting in the output "25".
A is decremented by 1, so A becomes 4.
Step 3: Iteration 2
A (4) is still greater than or equal to B (3).
The square of A (4²) is displayed, resulting in the output "16".
A is decremented by 1, so A becomes 3.
Step 4: Iteration 3
A (3) is still greater than or equal to B (3).
The square of A (3²) is displayed, resulting in the output "9".
A is decremented by 1, so A becomes 2.
Step 5: Iteration 4
A (2) is still greater than or equal to B (3).
The square of A (2²) is displayed, resulting in the output "4".
A is decremented by 1, so A becomes 1.
Step 6: Iteration 5
A (1) is still greater than or equal to B (3).
The square of A (1²) is displayed, resulting in the output "1".
A is decremented by 1, so A becomes 0.
Step 7: Loop termination
Since A (0) is no longer greater than or equal to B (3), the loop terminates.
Therefore, The output generated by the code execution will be "25, 16, 9, 4, 1" as the squares of A (starting from 5 and decreasing by 1) are displayed in each iteration of the loop.
To know more about pseudocode , visit:
https://brainly.com/question/14040924
#SPJ11
Find the area of the figure
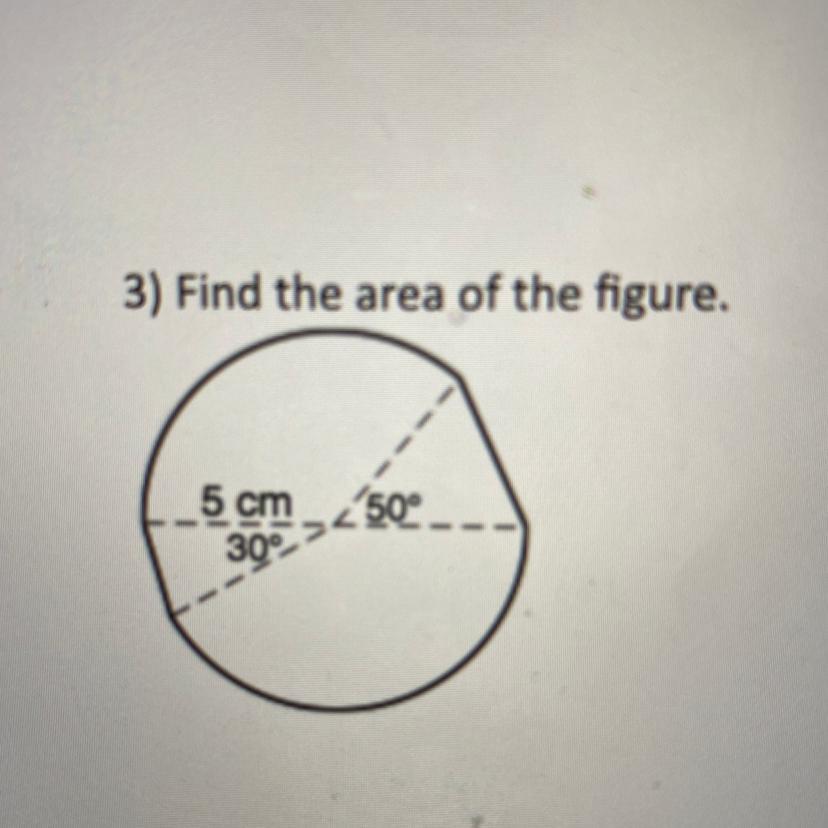
Answers
Answer:
A = 76.912Step-by-step explanation:
Area of triangle with angle of 30°:
\(A_1=\frac12\cdot 5^2\cdot\sin(30^o)=\dfrac{25}4=6.25\)
Area of triangle with angle of 50°:
\(A_2=\frac12\cdot 5^2\cdot\sin(50^o)=\dfrac{25}2\cdot0.766=9.575\)
Area of the rest of the figure:
\(A_3=\dfrac{(360-30-50)^o}{360^o}\cdot\pi\cdot5^2=\dfrac79\cdot\pi\cdot25 =61.087\)
Therefore:
\(A=A_1+A_2+A_3=6.25+9.575+61.087=76.912\)
use the kkt
Use the method of steepest ascent to approximate the solution to max z = -(x₁ - 3)² - (x₂ - 2)² s. t. (x₁, x₂) E R²
Answers
To approximate the solution and maximize the given objective function we need to find the steepest ascent direction and iteratively update the values of x₁ and x₂ to approach the maximum value of z.
The method of steepest ascent involves finding the direction that leads to the maximum increase in the objective function and updating the values of the decision variables accordingly. In this case, we aim to maximize the objective function z = -(x₁ - 3)² - (x₂ - 2)².
To find the steepest ascent direction, we can take the gradient of the objective function with respect to x₁ and x₂. The gradient represents the direction of the steepest increase in the objective function. In this case, the gradient is given by (∂z/∂x₁, ∂z/∂x₂) = (-2(x₁ - 3), -2(x₂ - 2)).
Starting with initial values for x₁ and x₂, we can update their values iteratively by adding a fraction of the gradient to each variable. The fraction determines the step size or learning rate and should be chosen carefully to ensure convergence to the maximum value of z.
By repeatedly updating the values of x₁ and x₂ in the direction of steepest ascent, we can approach the solution that maximizes the objective function z. The process continues until convergence is achieved or a predefined stopping criterion is met.
Learn more about fraction here:
https://brainly.com/question/10354322
#SPJ11
99 cookies were diveded into three piles in the ratios of 1:1/2:1/3. how many cookies were in the middle pile
Answers
To the total of 99 cookies, there are 27 cookies in middle pile.
Let's call the number of cookies in the first pile "x". Then, the number of cookies in the second pile is 1/2 of x, or (1/2)x, and the number of cookies in the third pile is 1/3 of x, or (1/3)x.
We know that the total number of cookies is 99, so we can write an equation:
x + (1/2)x + (1/3)x = 99
To solve for x, we can first find a common denominator:
(6/6)x + (3/6)x + (2/6)x = 99
(11/6)x = 99
x = (6/11) * 99
x = 54
So, there are 54 cookies in the first pile, (1/2)x = (1/2)*54 = 27 cookies in the second pile, and (1/3)x = (1/3)*54 = 18 cookies in the third pile. In the middle pile there are 27 cookies.
To know more about total number in pile:
https://brainly.com/question/14299907
#SPJ4
The area of the triangular

Answers
Answer:
24 \(cm^{2}\)
Step-by-step explanation:
a = \(\frac{bh}{2}\)
We have the base, we need the height. Use the Pythagorean Theorem
\(a^{2}\) + \(b^{2}\) = \(c^{2}\)
\(6^{2}\) + \(b^{2}\) = \(10^{2}\)
36 + \(b^{2}\) = 100 Subtract 36 from both sides
\(b^{2}\) = 64
\(\sqrt{b^{2} }\) = \(\sqrt{64}\)
b = 8
a = \(\frac{bh}{2}\)
a =\(\frac{6x8}{2}\) =\(\frac{48}{2}\) = 24
Step by step
The area of a triangle is found using
1/2 base x height
Since we don’t know height, we need to find the third leg of this right triangle first
Using Pythagorean theorem a^2 + b^2 = c^2
c^2 is the hypotenuse (diagonal) and b^2 is the base so our unknown is a^2
a^2 + 6^2 = 10^2
a^2 + 36 = 100
Subtract 36 from both sides to isolate our unknown variable
a^2 + 36 - 36 = 100 - 36
a^2 = 64
Now take square root of both sides to solve for a
a = 8 (height)
Now we have a height of 8 and a base of 6
Our formula again is
A = 1/2 base x height
A = (1/2) (6) (8)
A = 24
Problem solved!
gordon types 1800 words in 25 minutes. word per minute
Answers
Answer:
72
Step-by-step explanation:
words per minutes= 1800÷25=72
Match the vocabulary word with the correct definition.

Answers
Answer:
1=original image before transformation
2=shape or object that has been transformed
3=change made to shape or object
4=the mirror line
5=transformation in which figure flipped over line
Step-by-step explanation:
Answer:
1. pre-image the original shape or object that is being transformed
2. image is a shape or object that has been transformed
3. transformation is a change made to a shape or object.
4. line of reflection is the mirror line; the line across where a figure is flipped
5. reflection is a transformation in which the figure is flipped over a line to give a mirror image of the original figure
Step-by-step explanation:
How many different outcomes are there when
rolling?
A. Three standard dice?
B. Four standard dice?
c. Two 8 sided dice?
D. Three 12 sided dice?
Answers
a) There are three dice, the total number of different outcomes is 6 * 6 * 6 = 216.
b) The total number of different outcomes is 6 * 6 * 6 * 6 = 1296.
c) there are two dice, the total number of different outcomes is 8 * 8 = 64.
d) The total number of different outcomes is 12 * 12 * 12 = 1728.
A. When rolling three standard dice, each die has 6 possible outcomes (numbers 1 to 6). Since there are three dice, the total number of different outcomes is 6 * 6 * 6 = 216.
B. When rolling four standard dice, each die still has 6 possible outcomes. Therefore, the total number of different outcomes is 6 * 6 * 6 * 6 = 1296.
C. When rolling two 8-sided dice, each die has 8 possible outcomes (numbers 1 to 8). Since there are two dice, the total number of different outcomes is 8 * 8 = 64.
D. When rolling three 12-sided dice, each die has 12 possible outcomes (numbers 1 to 12). Therefore, the total number of different outcomes is 12 * 12 * 12 = 1728.
Learn more about standard dice here:
https://brainly.com/question/17273074
#SPJ11
Do the following points represent a function? (0,2) (1,4) (0,4) (3,9) (5,8)
Answers
Why not? Focus on the two points (0,2) and (0,4)
We have the x value x = 0 show up twice. Any time x repeats itself like this, it leads to "not a function" as the result.
In other words, the input x = 0 leads to multiple outputs y = 2 and y = 4 at the same time. A function is only possible if every x input leads to exactly one y output.
If you are a visual learner, then plot all of the points on the same xy grid. Then notice how (0,2) and (0,4) fail the vertical line test to show we don't have a function.
Side note: The y values can repeat themselves in a function.
the $5\times 5$ grid shown contains a collection of squares with sizes from $1\times 1$ to $5\times 5$. how many of these squares contain the black center square?
Answers
the total number of squares that contain the black center square is\($1 + 4 + 9 + 16 + 1 = \boxed{31}$.\)
To solve this problem, we need to count the number of squares of each size that contain the black center square.
There is only one square of size\($5\times 5$\), which is the entire grid and obviously contains the black center square.
For squares of size\($4\times 4$\), there are \($4$\)possible squares that contain the black center square (one for each corner).
For squares of size\($3\times 3$,\) there are 9 possible squares that contain the black center square (one for each position that the center square could occupy, and then each of those squares could be oriented in three different ways).
For squares of size $2\times 2$, there are $16$ possible squares that contain the black center square (one for each pair of adjacent squares).
For squares of size \($1\times 1$\), there is only one possible square that contains the black center square (the center square itself).
Therefore, the total number of squares that contain the black center square is\($1 + 4 + 9 + 16 + 1 = \boxed{31}$.\)
learn more about squares
https://brainly.com/question/14198272
#SPJ11
There are 11 squares containing the black center square in the 5x5 grid.
To find the number of squares that contain the black center square, we'll consider the sizes of the squares and their positions in the 5x5 grid.
The black center square is a 1x1 square itself, so that's 1 square.
For 2 x 2 squares containing the center square, there are 4 possible positions (the center square can be in any corner). So, that's 4 squares.
For 3x3 squares containing the center square, there is only 1 possible position (the center square is exactly in the middle). So, that's 1 square.
4. For 4x4 squares containing the center square, there are 4 possible positions (the center square can be in any corner). So, that's 4 squares.
5. For 5x5 squares containing the center square, there is only 1 possible position (the center square is exactly in the middle).
So, that's 1 square.
Now, we'll add up the number of squares we found in each step:
1 + 4 + 1 + 4 + 1 = 11.
For similar question on squares.
https://brainly.com/question/23305357
#SPJ11
Noah bought 5 CDs and a DVD for a total of $57. The DVD cost $12. The CDs were each the same price. How much did Noah pay for each CD?
•Equation:
•So, Noah paid ______ for each CD.
Answers
If x = -6, which equation is true?
A 0 = 2(x - 6)
B 36 = 3(6 - x)
C 27 = 3(x – 3)
D -30 = 6x - 6
Answers
Answer:
B
Step-by-step explanation:
A. 0 = 2((-6) - 6)
0 = -12 - 12
0 = -24
False.
B. 36 = 3(6 - (-6))
36 = 3(6+6)
36 = 3 * 12
36 = 36
True
Answer:
36 = 3(6 - x)
Step-by-step explanation:
Option A is false.
Option C is false.
Option D is false.
With all of the other options being false, we are left with option B. If we take the equation 36 = 3(6 - x) and change it to 35 = 3(6 - (-6)), we can confirm that it it correct.
Show that the triangles are similar and write a similarity statement.E1427AC 18D21BZACBACEDCSo AABC ~ A
Answers
Two triangles are similar if the ratio of their corresponding side equal'
Triangle
Because
Corresponding sides are
Therefore,
Triangle

Which answer choice correctly shows 579 written as a Roman Numeral? A. MLXXIV B. DLXXIX C. DLXXVIIII D. DLXXIV
Answers
Find the missing length of the triangle. 12 in 85 in.

Answers
Answer:
From Pythagoras Theorem
The square of the hypotenuse is equal to the sum of the squares of the other two sides
C² = 12² + 35²
C= √12²+35²
C= 37in
Answer:
side c = 37 in.
Step-by-step explanation:
side c is the hypotenuse as it is opposite of right angle (90 degree ).
12 and 35 are the two other smaller sides of the given right angles triangle.
using pythagoras theorem to find side c
a^2 + b^2 = c^2
12^2 + 35^2 = c^2
144 + 1225 = c^2
1369 = c^2
\(\sqrt{1369}\) = c
37 = c
HELP ASAP ILL MARK BRAINLIEST
What is the distance between tho y-Intercept of the function (x) = 3(2) and tho y-intercept of the the function g(x) represented by the table below?
х
g(x)
-5
15
- 2
3
2
-13
и |
-25
2 units
3 units
O 8 units
O 9 units

Answers
Im pretty sure its 8 units