Two solutions of the equation are Ax + By = 1 are (3, -1) and (-4, -2). Find A and B

Answer:

(1,7)

(0,2)

(-1,-3)

(-2,-8)

put dots on these points and put a line through all of them making on line

The statement "If the conclusion of an argument is a tautology, then the counterexample set of that argument must be inconsistent" is true.

Let's understand why?

Explanation:

An argument with a tautology conclusion is an argument that arrives at a conclusion that is always true, regardless of the truth values of the premises. In other words, it is impossible for the premises to be true while the conclusion is false.

This means that any attempt to find a counterexample that disproves the conclusion will always fail, as there is no possible scenario in which the conclusion is false.

The counterexample set of an argument is the set of all possible scenarios in which the premises are true but the conclusion is false. If the conclusion is a tautology, then there is no possible scenario in which the conclusion is false, and thus the counterexample set is empty. An empty counterexample set is equivalent to an inconsistent counterexample set, as it means that there is no consistent scenario in which the conclusion is false.

Therefore, if the conclusion of an argument is a tautology, then the counterexample set of that argument must be inconsistent.

Hence, the statement is true.

Learn more about tautology here:

https://brainly.com/question/30195011

#SPJ11

Answer:

b.332.2

Step-by-step explanation:

Therefore, The probability that the customer likes neither hot nor iced coffee is 0. This can be calculated by subtracting the probability of the customer liking hot coffee or iced coffee from 1.

The probability that the customer likes neither hot nor iced coffee can be calculated by subtracting the probability of the customer liking hot coffee or iced coffee from 1. Let A be the event that the customer likes neither hot nor iced coffee. Then, P(A) = 1 - P(H) - P(I). If P(H) = 0.6 and P(I) = 0.4, then P(A) = 1 - 0.6 - 0.4 = 0. Therefore, the probability that the customer likes neither hot nor iced coffee is 0.
To find the probability of an event, we need to divide the number of favorable outcomes by the total number of possible outcomes. Here, the customer can either like hot coffee, iced coffee, or neither. Since the customer can only like one of the two options, we can use the complement rule to find the probability of the customer not liking either. We subtract the sum of probabilities of the customer liking hot and iced coffee from 1.
Therefore, The probability that the customer likes neither hot nor iced coffee is 0. This can be calculated by subtracting the probability of the customer liking hot coffee or iced coffee from 1.

To know more about probability visit :

https://brainly.com/question/13604758

#SPJ11

Yes, both angles are equal—A = B = 148°—and the corresponding angles of two parallel lines are also equal—x = 25°.

How do you define an angle?

An angle in an aeroplane figure is a figure created by two shafts or lines that meet at the same endpoint. Angle is derived from the Latin word angulus, which also means corner. An angle's two shafts are referred to as its sides, and its common endpoint is known as its vertex. The angle that the plane is lying at need not be in Euclidean space. When two airplanes intersect in Euclidean or another space to form an angle, the angle is said to be a dihedral angle. The arc is

∠A = 6 x 25 - 2 = 148°

∠B = 4 x 25 + 48 = 148°

Therefore , proved that ∠A = ∠B .

Learn more about Angles click here:

brainly.com/question/25770607

#SPJ1

angle A equals 6x-2, angle b equals 4x+48​ both angles are the same

True/ false

The 354 ml bottle of nighttime cough suppressant contains approximately 147.5 mg of doxylamine succinate, based on a 30 ml dose containing 12.5 mg.



To find the number of milligrams of doxylamine succinate in the entire 354 ml bottle of nighttime cough suppressant, we can use a proportion based on the ratio of volume to dose.

Given:

Volume of the bottle = 354 ml

Dose of the bottle = 30 ml

Doxylamine succinate in one dose = 12.5 mg

Let x be the number of milligrams of doxylamine succinate in the entire 354 ml bottle.

Using the proportion:

(12.5 mg / 30 ml) = (x mg / 354 ml)

Cross-multiplying:

30 * x = 12.5 * 354

x = (12.5 * 354) / 30

x ≈ 147.5 mg

Therefore, there are approximately 147.5 milligrams of doxylamine succinate in the entire 354 ml bottle of nighttime cough suppressant.

To learn more about ratio click here

brainly.com/question/13419413

#SPJ11



Step-by-step explanation:

Let the number be x, then

\( \frac{x}{2 + 7} \\ \frac{x}{9} \)

Answer:

  non-linear

Step-by-step explanation:

The given points do not fall on a straight line when plotted on a graph.

__

If you realize that the x-values go up, and the y-values go down and up, then you know the relation cannot be linear. That is, its graph cannot be a straight line.

We get equation B from equation A by Multiplying /dividing both sides by the same non-zero constant i.e., 4.

A non-zero constant polynomial is written as: p(x) = c, where c is a non-zero real number. This means that for all possible values of x, p(x) = c, i.e. it is never 0. Thus, a non-zero constant polynomial does not have any zeroes.

Given

\(\frac{x}{4}+1 =-3\)

Multiply/divide both sides by the same non-zero constant i.e., 4.

⇒ \(4\times(\frac{x}{4}+1) =4\times-3\)

⇒ x + 4 = -12

Hence, We get equation B from equation A by Multiplying /dividing both sides by the same non-zero constant i.e., 4.

Find out more information about non-zero constant here

https://brainly.com/question/14686792

#SPJ3

The measure of the other diagonal line is 6.8 inches

A kite is a quadrilateral with two distinguishable consecutive sides. The area of a kite can be calculated by the multiplication of the two diagonal lines divided by 2.

Mathematically, we have:

\(\mathbf{A = \dfrac{pq}{2}}\)

where:

∴

Using the formula for an area of a kite to determine the other diagonal length, we have:

\(\mathbf{51.68 \ inches^2 = \dfrac{15.2 \ inches \times q}{2}}\)

\(\mathbf{q = \dfrac{51.86 \ inches^2 \times 2}{15.2 inches} }\)

q = 6.8 inches

Learn more about the area of kite here:

https://brainly.com/question/2292872

Answer:

x = -2

Step-by-step explanation:

3/2 (x-5) - 3/2 = 9x/2

3x/2 - 15/2 - 3/2 = 9x/2 ... alldenominator

are 2 so we can multiply all term by 2

2(3x/2 - 15/2 - 3/2 = 9x/2)

3x - 15 - 3 = 9x ... simplify it

3x - 12 = 9x

-12 = 9x - 3x ... take 3x to the left

-12 = 6x ... simplify

6x/6 = -12/6 ... dividing both side by 6

x = -2 ... simplify and solve x

The approximation range for the square root of 3 provided by Archimedes is quite good. The decimal value falls within the given range, demonstrating its accuracy.

What is Pi?

The reciprocal of the ratio of a circle's circumference to its diameter is known as pi (), a mathematical constant. Because it is irrational, it cannot be written as a fraction or a finite decimal. Pi has a value of roughly 3.14159, however it goes on forever without repeating any decimals.

To approximate the value of pi based on the inscribed figures, we can use the perimeter of the regular polygons as an approximation for the circumference of the unit circle.

Starting with a regular hexagon, we know its perimeter is 6. This is an approximation for the circle's circumference, 2 pi. Therefore, we can say that pi ≈ 6/2 = 3.

To calculate the perimeters of the subsequent inscribed polygons, we can double the number of sides each time. Let's go through the doubling process:

Hexagon: Perimeter = 6

Dodecagon (12-gon): Perimeter = 12

24-gon: Perimeter = 24

48-gon: Perimeter = 48

96-gon: Perimeter = 96

192-gon: Perimeter = 192

384-gon: Perimeter = 384

768-gon: Perimeter = 768

Now, we can use the formula for the perimeter of a regular polygon inscribed in a unit circle, which is given by:

Perimeter ≈ 2 * n * sin(π/n)

where n is the number of sides of the polygon.

Using this formula, we can calculate the approximate value of pi for each polygon:

Hexagon: pi ≈ 6/2 = 3.00 (as given)

Dodecagon: pi ≈ 12/(2 * sin(π/12)) ≈ 3.10582854123

24-gon: pi ≈ 24/(2 * sin(π/24)) ≈ 3.13262861328

48-gon: pi ≈ 48/(2 * sin(π/48)) ≈ 3.13935020305

96-gon: pi ≈ 96/(2 * sin(π/96)) ≈ 3.14103195089

192-gon: pi ≈ 192/(2 * sin(π/192)) ≈ 3.14145247229

384-gon: pi ≈ 384/(2 * sin(π/384)) ≈ 3.14155760791

768-gon: pi ≈ 768/(2 * sin(π/768)) ≈ 3.14158389215

As the number of sides increases, the approximation of pi becomes more accurate. The value of pi based on the inscribed 768-gon is approximately 3.14158389215.

Regarding Archimedes' approximation of the square root of 3, let's evaluate the range mentioned:

265/153 < √3 < 1351/780

To determine how good this approximation is as a decimal, we can calculate the actual value of the square root of 3 and compare it to the given range:

√3 ≈ 1.73205080757

Comparing this value to the range, we can see:

265/153 ≈ 1.73202614379

1351/780 ≈ 1.73205128205

Hence, the approximation range for the square root of 3 provided by Archimedes is quite good. The decimal value falls within the given range, demonstrating its accuracy.

To learn more about pi follow the given link:

https://brainly.com/question/457655

#SPJ4

Answer:

{(3, 5), (2, 5), (3,8)}

Step-by-step explanation:

separate the x's & y's & put them in separate brackets

Answer:

363.22

Step-by-step explanation:

Method 1:

You could find the whole figure surface area than divided by 1/2

Method 2: (the one I'm going to personally be doing)

Break the figure into two rectangular figures

Formula for surface area of rectangular prism:

A = 2(width x length + height x length + height x width)

Figure 1:

A = 2(width x length + height x length + height x width)

height = 3.8 yd

length = 10.1 yd

width = 4.3 yd

A = 2((4.3) x (10.1) + (3.8) x (10.1) + (3.8) x (4.3))

A = 2(98.15)

A = 196.3

Figure 2:

A = 2(width x length + height x length + height x width)

height = 8.4 yd

length = 10.1 yd

width = 2 yd

A = 2((2) x (10.1) + (8.4) x (10.1) + (8.4) x (2))

A = 2(121.84)

A = 243.68

There is overlapping surface area that shouldnt be include so we need to subtract it...

For one face of figure 1

3.8 x 10.1 = 38.38

Total:

Figure 1 + Figure 2 - 2(one face)

196.3 - 38.38 = 157.92

243.68 - 38.38 = 205.3

205.3 + 157.92 = 363.22

Answer: 14.1421356237

Step-by-step explanation: We should know that 200 can be written in radical form (√200 = q × q = q2).  To find the square root of 200, first you can ask yourself whether √200 is a perfect square, in which it isn’t because it doesn’t equal a whole number. Next, ask yourself if √200 is a rational or irrational number, in which it is an irrational number. After, determine whether √200 can be simplified, which in this case can be simplified to 200 = 10√2 which makes it easier to calculate the square root of 200. Lastly, the easiest and most boring way to calculate the square root of 200 is to use your calculator! Simply type in 200 followed by √x to get the answer. We did that with our calculator and got the following answer with 9 decimal numbers:

√200 ≈ 14.142135624

The percentage of those who were married were also obese is: 34.7% (147/424; Option B)

Now,

The percentage of number of married participants who were obese is calculated by: dividing the former (147) by the total number of married participants(424)

=> Percentage of married participants who were obese = 147/424.

Hence, The percentage of those who were married were also obese is: 34.7% (147/424; Option B)

To learn more about percentages, refer to the link: https://brainly.com/question/24304697

#SPJ4

(COMPLETE QUESTION:

A 2009 study analyzed data from the National Longitudinal Study of Adolescent Health. Participants were followed into adulthood. Each study participant was categorized as to whether they were obese (BMI >30) or not and whether they were dating, cohabiting, or married. The table below summarizes the results.

Dating Cohabiting Married Total

Obese 81 103 147 331

Not Obese 359 326 277 962

Total 440 429 424 1293

What percentage of those who were married were obese? (Round your answer to 1 decimal place.)

A. 32.8% (424/1293)

B. 34.7% (147/424)

C. 25.6% (331/1293)

D. 44.4% (147/331))

Sandy will need to purchase two sections of the siding, which will cost 2 x $27.30 = $54.60.

Sandy will need to purchase three sections of the special siding. To calculate the total cost of the siding, we first need to calculate the total area that needs to be covered.
The area of the shaded exterior wall can be calculated by multiplying its height by its width. Let's assume the wall is 8 feet high and 10 feet wide. Therefore, the area of the wall is 8 x 10 = 80 square feet.
The area of each rectangular face of the roof can be calculated by multiplying its length by its width. Let's assume each face is 8 feet by 6 feet. Therefore, the area of each face is 8 x 6 = 48 square feet.
To calculate the total area that needs to be covered, we add the area of the wall and the two faces of the roof. So, the total area that needs to be covered is 80 + 48 + 48 = 176 square feet.
Each section of the special siding covers 8 x 12 = 96 square feet. So, to cover the 176 square feet of the playhouse, Sandy will need to purchase two sections of the siding, which will cost 2 x $27.30 = $54.60.

Learn more about total cost here:

https://brainly.com/question/30355738

#SPJ11

9514 1404 393

Explanation:

The quadrilateral will be a parallelogram if the diagonals bisect each other. That will be the case if the sums of their end-point coordinates are the same.

  A + C = (-3, 6) +(9, -9) = (6, -3)

  B + D = (6, 0) +(0, -3) = (6, -3)

Both diagonals have their midpoint at (3, -1.5), so the diagonals are mutual bisectors. The figure ABCD must be a parallelogram.

___

The midpoint of AC is (A+C)/2 = (6, -3)/2 = (3, -1.5).

Answer:

b

Step-by-step explanation:

b is the answer

Answer:

27x + 45 + 9x

37x + 45

it's here

The simplified expression for (f ∘ g)(x) is 2 + x (option d).

To find and simplify (f ∘ g)(x), we need to substitute the expression for g(x) into f(x) and simplify.

Given:

f(x) = log₃(9x)

g(x) = \(3^x\)

Substituting g(x) into f(x):

(f ∘ g)(x) = f(g(x)) = log₃\((9 * 3^x)\)

Now, we simplify the expression:

log₃\((9 * 3^x)\) = log₃(9) + log₃\((3^x)\)

Since logₓ(a * b) = logₓ(a) + logₓ(b), we have:

log₃(9) + log₃\((3^x)\) = log₃\((3^2)\) + x

Using the property logₓ\((x^a)\) = a * logₓ(x), we get:

log₃\((3^2)\) + x = 2 * log₃(3) + x

Since logₓ\((x^a)\) = a, where x is the base, we have:

2 * log₃(3) + x = 2 + x

Therefore, (f ∘ g)(x) simplifies to:

(f ∘ g)(x) = 2 + x

So, the correct answer is (d) 2 + x.

To know more about expression, refer here:

https://brainly.com/question/31800038

#SPJ4

Complete Question:

Given f(x)=log₃(9x) and g(x)=\(3^x\). Find and simplify (f ∘ g)(x)

(a) 2x

(b) x

(c) \(27^x\)

(d) 2+x

(e) None of these.

Answer:

  a) see attached

  b) 15015 meters

Step-by-step explanation:

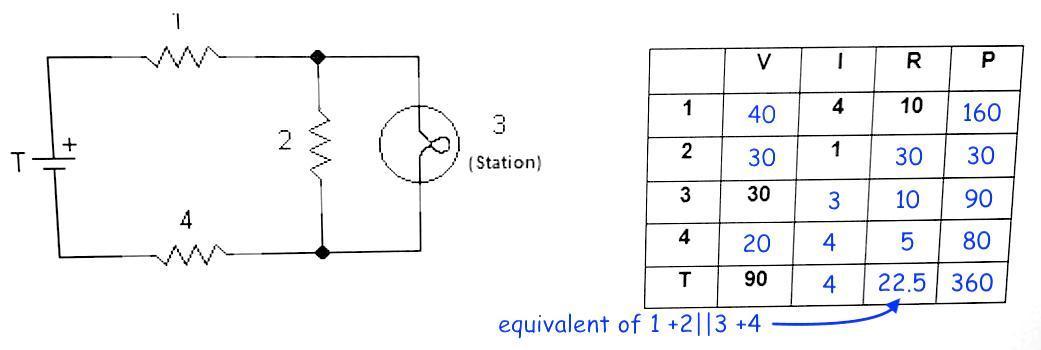
You want the voltage, current, resistance, and power for each component of the circuit shown in the diagram.

The relevant circuit relations are ...

Given current and resistance for element 1, we immediately know its voltage is ...

  V = IR = (4)(10) = 40 . . . . volts

Given the voltage on element 3, we know that parallel element 2 has the same voltage: 30 volts.

Given the voltage at T is 90 volts, the sum of voltages on elements 1, 2, and 4 must be 90 volts. That means the voltage on element 4 is ...

  90 -(40 +30) = 20

The current in elements 1, 4, and T are all the same, because these elements are in series. They are all 4 amperes.

That 4 ampere current is split between elements 2 and 3. The table tells us that element 2 has a current of 1 ampere, so element 3 must have a current of ...

  4 - 1 = 3 . . . . amperes

The resistance of each element is the ratio of voltage to current:

  R = V/I

Dividing the V column by the I column gives the values in the R column.

Note that power source T does not have a resistance of 22.5 ohms. Rather, it is supplying power to a circuit with an equivalent resistance of 22.5 ohms.

Power is the product of voltage and current. Multiplying the V and I columns gives the value in the P column.

Note that the power supplied by the source T is the sum of the powers in the load elements.

We found that the transmitter is receiving a power of 90 watts, so its operating frequency is ...

  (90 W)×(222 Hz/W) = 19980 Hz

Then the wavelength is ...

  λ = c/f

  λ = (3×10⁸ m/s)/(19980 cycles/s) ≈ 15015 m/cycle

The wavelength of the broadcast is about 15015 meters.

__

Additional comment

The voltage and current relations are "real" and used by circuit analysts everywhere. The relationship of frequency and power is "made up" specifically for this problem. You will likely never see such a relationship again, and certainly not in "real life."

Kirchoff's voltage law (KVL) means the sum of voltage rises (as at T) will be the sum of voltage drops (across elements 1, 2, 4).

Kirchoff's current law (KCL) means the sum of currents into a node is equal to the sum of currents out of the node. At the node between elements 1 and 2, this means the 4 amps from element 1 into the node is equal to the sum of the currents out of the node: 1 amp into element 2 and the 3 amps into element 3.

As with much of math and physics, there are a number of relations that can come into play in any given problem. You are expected to remember them all (or have a ready reference).

<95141404393>

The relation that can be formed by obersving the Cartesian Plane is y = 5x

What is Co-ordinate Geometry?

The study of geometry using coordinate points is known as coordinate geometry (or analytic geometry). It is possible to estimate the distance between two points, divide lines in a m:n ratio, identify the midpoint of a line, calculate the area of a triangle in the Cartesian plane, and so on using coordinate geometry.

Solution:

By analysing the given Cartesian Plane

it can be observed that the rate of change of y with respect to x

is 5 times

Therefore, the relation that can be formed by obersving the Cartesian Plane is y = 5x

To learn more about Co-ordinate Geometry from the given link

https://brainly.com/question/25042607

#SPJ1

Answer:

the answer is 71

Step-by-step explanation:

423/6

42÷6=7

42-42=0

6÷3=×

30÷6=5

70.5--> 71

The sum of the faces is going to fall in the range {2, 3, 4, …, 12}, which contains five prime numbers {2, 3, 5, 7, 11}. You can only have one sum at a time, so these outcomes are mutually exclusive. Then

Pr[sum is prime] = Pr[sum = 2] + Pr[sum = 3] + … + Pr[sum = 11]

• sum = 2 can only happen in 1 way (1 + 1)

• sum = 3 can happen in 2 ways (1 + 2, 2 + 1)

• sum = 5 can happen in 4 ways (1 + 4, 2 + 3, 3 + 2, 4 + 1)

• sum = 7 can happen in 6 ways (1 + 6, 2 + 5, …, 6 + 1)

• sum = 11 can happen in 2 ways (5 + 6, 6 + 5)

There are a total of 6² = 36 possible sums that can be rolled, each with probability 1/36 of occurring, so the probability of getting a prime sum is

(1 + 2 + 4 + 6 + 2)/36 = 15/36 = 5/12

To find an explicit particular solution to the given initial value problem, we can use the separation of variables and integration. The particular solution is (y^2)/2 = x tan^(-1)(x) - ln|1 + x^2|/2 + 1/2

Rearranging the equation, we have:

y dy = tan^(-1)(x) dx

Now, we can separate the variables and integrate both sides:

∫(y dy) = ∫(tan^(-1)(x) dx)

Integrating both sides, we get:

(y^2)/2 = ∫(tan^(-1)(x) dx)

To evaluate the integral on the right side, we can use integration by parts. Let u = tan^(-1)(x) and dv = dx. Then, du = dx/(1 + x^2) and v = x.

Applying the integration by parts formula, we have:

∫(tan^(-1)(x) dx) = x tan^(-1)(x) - ∫(x/(1 + x^2) dx)

Simplifying the expression, we get:

∫(tan^(-1)(x) dx) = x tan^(-1)(x) - ln|1 + x^2|/2

Substituting this result back into the previous equation, we have:

(y^2)/2 = x tan^(-1)(x) - ln|1 + x^2|/2 + C where C is the constant of integration.

Now, we can apply the initial condition y(0) = 1 to find the particular solution. When x = 0, the equation becomes:

(1^2)/2 = 0 tan^(-1)(0) - ln|1 + 0^2|/2 + C

Simplifying this equation, we have:

1/2 = C Therefore, the particular solution is:

(y^2)/2 = x tan^(-1)(x) - ln|1 + x^2|/2 + 1/2 This represents the explicit particular solution to the given initial value problem.

Learn more about integration here: brainly.com/question/31744185

#SPJ11

Answer:

47 is a prime number because it has only two factors, 1 and 47.

Step-by-step explanation:

Your welcome.

Answer: A prime number is a number that can only be divided evenly by 1 and itself. 47 is a prime number because it can only be divided evenly by 1 and 47. It cannot be divided evenly by any other number. That's why we say 47 is a prime number. ✅

PLEASE MAKE THIS A BRANLIEST ANSWER!!!

We can write the given partial equilibrium model on the form Ax = d, and then use Cramer's rule to solve for the values of Qs* and P*.

To write the model on the form Ax = d, we need to express the equations in a matrix form.

The given equations are:

Qd = a1 + b1P

Qs = a2 + b2(P - t)

We can rewrite these equations as:

-Qd + 0P + Qs = a1

0Qd - b2P + Qs = a2 - b2t

Now, we can represent the coefficients of the variables and the constants in matrix form:

| -1 0 1 | | Qd | | a1 |

| 0 -b2 1 | * | P | = | a2 - b2t |

| 0 1 0 | | Qs | | 0 |

Let's denote the coefficient matrix as A, the variable matrix as x, and the constant matrix as d. So, we have:

A * x = d

Using Cramer's rule, we can solve for the variables Qs* and P*:

Qs* = | A_qs* | / | A |

P* = | A_p* | / | A |

where A_qs* is the matrix obtained by replacing the Qs column in A with d, and A_p* is the matrix obtained by replacing the P column in A with d.

By calculating the determinants, we can find the values of Qs* and P*.

It's important to note that Cramer's rule allows us to solve for the variables in this system of equations. However, the applicability of Cramer's rule depends on the properties of the coefficient matrix A, specifically its determinant. If the determinant is zero, Cramer's rule cannot be used. In such cases, alternative methods like substitution or elimination may be required to solve the equations.

Learn more about matrix here:

https://brainly.com/question/29132693

#SPJ11