12.1.38 Find two vectors parallel to v with three times the magnitude of v v=(7,-3) Select the correct two vectors below. □ A. (-21,9) □B. 7 3 58 58 -7 3 158、158 n| □E· (9,-21) AT Click to select your answer(s) and then click Check Answer
Answers
Vector A: (-21, 9) and Vector E: (9, -21) are two vectors parallel to v with three times the magnitude of v. vectors A and E are two vectors parallel to v with three times the magnitude of v.
To calculate the two vectors, we need to first calculate the magnitude of vector v. Magnitude of v = √(7² + (-3)²) = √58 = 7.615.
Next, we multiply this magnitude by 3 to get the magnitude of the required vectors. Magnitude of the required vectors = 7.615 x 3 = 22.845.
We now have the magnitude and direction of the required vectors. To calculate the components of the vectors, we use the following formula:
A = (magnitude) x (cosθ, sinθ)
Where θ is the angle made by the vector with the x-axis.
For vector A:
Magnitude = 22.845
Angle made by vector A with x-axis = 0 degrees
Hence, components of vector A = (22.845 x cos0, 22.845 x sin0) = (-21, 9)
Similarly, for vector E:
Magnitude = 22.845
Angle made by vector E with x-axis = 180 degrees
Hence, components of vector E = (22.845 x cos180, 22.845 x sin180) = (9, -21)
To know more about vectors refer here:
https://brainly.com/question/29740341
#SPJ11
Related Questions
if you add 10 to every value of a data set, what happens to the standard deviation?
Answers
The standard deviation of the data set will increase by a factor of 10. This is because standard deviation measures how much variation or dispersion exists from the mean of a data set. Adding 10 to every value of the data set will increase the overall spread of the data and thus increase the standard deviation.
To prove this mathematically, let's consider a data set A with mean M and standard deviation SD. Let's add 10 to every value of the data set to get a new data set B. The mean of set B is M+10 and the standard deviation of set B is SD'. The formula for SD' is:
SD':\(\sqrt{(x_{1} -(M+10))^{2} +(x_{2} -(M+10))^2+ (x_{3}-(M+10))^2 +...+ (x_{n}-(M+10))^2)/n }\) We can simplify this by substituting the values for the xi:
SD' =\(\sqrt{(((x_{1}-M-10)^2 + (x_{2}-M-10)^2 + (x_{3}-M-10)^2 +...+ (x_{n}-M-10)^2)/n) }\) Now let's consider the original data set A and its standard deviation SD:
SD =\(\sqrt{(((x_{1}-M)^2 + (x_{2}-M)^2 + (x_{3}-M)^2 +...+ (x_{n}-M)^2)/n) }\) ,We can substitute the values for xi in this formula as well:
SD= \(\sqrt{ (((x_{1}-M-10)^2 + (x_{2}-M-10)^2 + (x_{3}-M-10)^2 +...+ (x_{n}-M-10)^2)/n)}\) If we compare SD and SD', we can see that they are identical, except that the value of M has been replaced with M+10. This means that when we add 10 to every value of the data set, the standard deviation increases by a factor of 10.
To know more about standard deviation refer to the link brainly.com/question/23907081
#SPJ4
1
3x +2y - 5z
If
y-42
X
=
find the value of x when y = 6 and z
2
3y
Answers
Answer:
hmmmm i saw something about 13?????
Step-by-step explanation:
Victor borrowed money at 5. 25 percent simple annual interest. At the end of the year, the interest on the loan is $255. 94. What was the amount of the loan? $13. 44 $134. 37 $1,343. 69 $4,875. 5.
Answers
Answer:
I think it is 1343.69.
Step-by-step explanation:
George is making a pennant for his favorite baseball team he wants the sbort edge to be 14 inches and full length to be 24 inches what is the length of diagonal said AB
Answers
The length of diagonal AB is approximately 24.4 inches.
We have,
If we assume that the pennant is a right triangle with one of the legs being 14 inches (the short edge) and the other leg is unknown, we can use the Pythagorean theorem to find the length of the diagonal.
According to the Pythagorean theorem,
14² + x² = 24²
where x is the length of the other leg (the one we are trying to find).
Solving for x,
x² = 24² - 14²
x² = 400
x = 20
The length of the other leg of the triangle is 20 inches, and using the Pythagorean theorem, we can find the length of the diagonal:
AB = √(14² + 20²) = √(596) ≈ 24.4 inches
Thus,
The length of diagonal AB is approximately 24.4 inches.
Learn more about the Pythagorean theorem here:
https://brainly.com/question/14930619
#SPJ1
You need to create a fenced off region of land for cattle to graze. The grazing area must be a total of 500 square feet, surrounded by a fence, and in the shape of a regular polygon. Within this grazing area, the length of the apothem must be 10 feet long. Part I. Find the total perimeter of the grazing area. Part II. If the cost of the fence is $7.95 per linear foot, how much will it cost to place a fence around the entire grazing area
Answers
Using area of regular Polygon, the perimeter of the total grazing area of regular polygon is 100 feet and the cost to place a fence around the entire grazing area is $795.
According to the question,
You need to create a fenced off region of land for cattle to graze. The grazing area must be a total of 500 square feet, surrounded by a fence, and in the shape of a regular polygon.
Within this grazing area, the length of the apothem must be 10 feet long.
In part 1 we asked to find the total perimeter of the grazing area using below polygon formulaThe formula of the area of regular polygon = ap/2
Where a is apothem and p is the perimeter.
500 = 10 x p/2
1,000 = 10 x p
100 = p
Hence the perimeter of regular polygon the total grazing area is 100 feet.
In part 2, the cost of the fence is $7.95 per linear foot, how much will it cost to place a fence around the entire grazing areaNow cost of fencing 1 foot = $7.59
So, cost of fencing 100 feet = 7.59 x 100 = 759
Hence, the cost to place a fence around the entire grazing area of polygon is $795.
Learn more about polygon here
https://brainly.com/question/13310667
#SPJ4
Celeste makes a conjecture that the perimeter of a square whose sides are an odd
integer is always even. Which choice is the best proof of her conjecture?
Answers
Answer:
top left
Step-by-step explanation:
1) If total costs for a product are given by C(x) = 1760 + 8x + 0.6x2 and total revenues are given by R(x) = 100x -0.4x2, find the break-even points. =
2) If total costs for a commodity are given by C(x) = 900 +25x and total revenues are given by R(x) = 100x - x2, find the break-even points. 3) Find the maximum revenue and maximum profit for the functions described in Problem #2.
Answers
a) The break-even points for the given cost and revenue functions are approximately x = 16.526 and x = 6.474.
b) The break-even points for the given cost and revenue functions are approximately x = 12.225 and x = 62.775.
c) The maximum profit for the given cost and revenue functions is approximately $843.75.
a) To find the break-even points, we need to determine the values of x where the total costs (C(x)) equal the total revenues (R(x)). We set C(x) = R(x) and solve for x:
C(x) = R(x)
1760 + 8x + 0.6x² = 100x - 0.4x²
Combining like terms and rearranging the equation, we get:
1x² - 92x + 1760 = 0
Solving this quadratic equation, we find two solutions for x:
x ≈ 16.526
x ≈ 6.474
b) Similarly, we set C(x) = R(x) and solve for x:
900 + 25x = 100x - x²
Rearranging the equation, we get:
x² - 75x + 900 = 0
Solving this quadratic equation, we find two solutions for x:
x ≈ 12.225
x ≈ 62.775
c) To find the maximum revenue, we need to determine the vertex of the revenue function R(x) = 100x - x². The x-coordinate of the vertex is given by x = -b / (2a), where a and b are the coefficients of the quadratic equation.
In this case, a = -1 and b = 100. Plugging in the values, we get:
x = -100 / (2 * -1) = 50
Substituting this value back into the revenue function, we find:
R(50) = 100(50) - (50)² = 5000 - 2500 = 2500
Therefore, the maximum revenue for the given cost and revenue functions is $2500.
To find the maximum profit, we need to subtract the total costs from the total revenues. Given that the cost function is C(x) = 900 + 25x, the profit function is P(x) = R(x) - C(x). Substituting the revenue and cost functions, we have:
P(x) = (100x - x²) - (900 + 25x)
P(x) = -x² + 75x - 900
To find the maximum profit, we need to determine the vertex of the profit function. Using the same formula as before, we find:
x = -75 / (2 * -1) = 37.5
Substituting this value back into the profit function, we find:
P(37.5) = -(37.5)² + 75(37.5) - 900 ≈ 843.75
To learn more about break-even points click on,
https://brainly.com/question/32090652
#SPJ4
Miguel has 3 1-gallon containers each 3/4 full of water how many cups of water are there
Answers
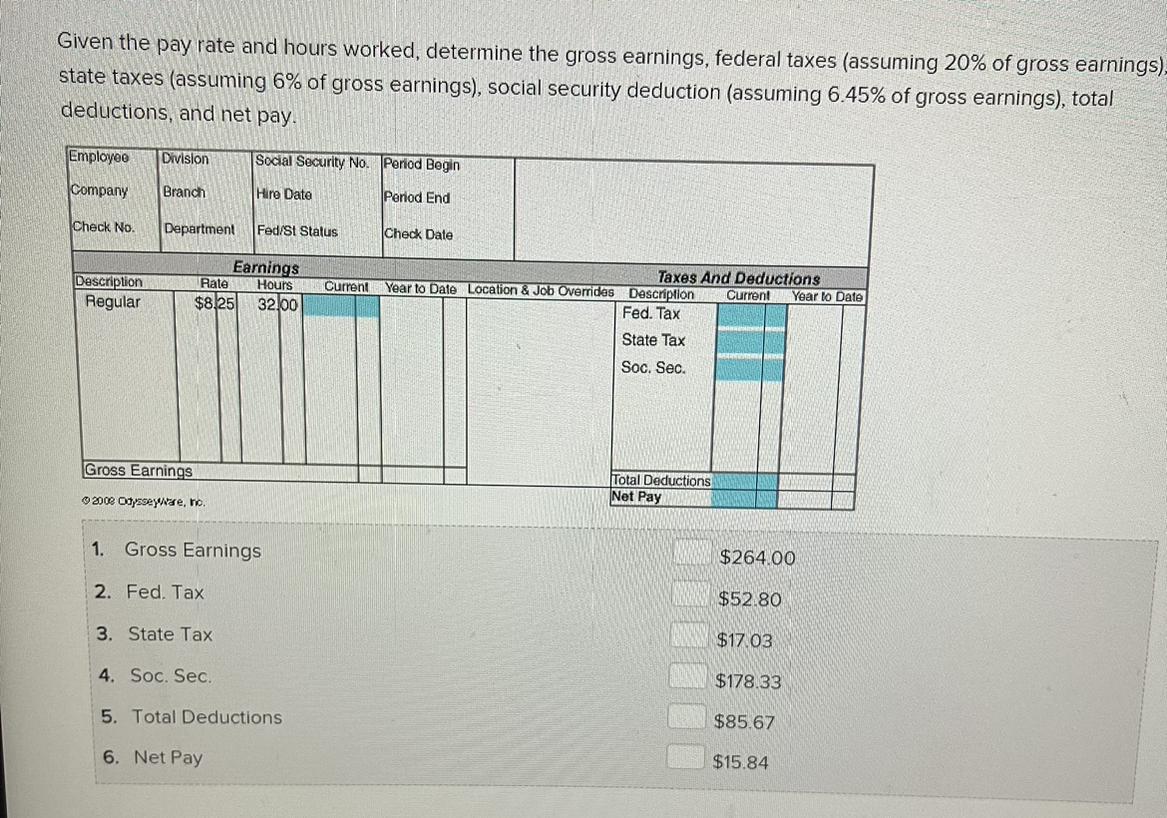
Given the pay rate and hours worked, determine the gross earnings, federal taxes (assuming 20% of gross earnings),
state taxes (assuming 6% of gross earnings), social security deduction (assuming 6.45% of gross earnings), total
deductions, and net pay.
1. Gross Earnings
2. Fed. Tax
3. State Tax
4. Soc. Sec.
5. Total Deductions
6. Net Pay
$264.00
$52.80
$17.03
$178.33
$85.67
$15.84
Answers
1. The gross income will be $264.
2. The federal tax will be $52.80.
3. The state tax will be $15.84.
4. The social security will be $7.03
5. The total deduction will be $85.67
6. The net pay is $178.33
How to calculate the values?Federal taxes = 20% of gross earnings
state taxes = 6% of gross earnings
social security deduction = 6.45% of gross earnings
Gross Income = $8.25 × 32
Gross Income = $264
Federal Tax will be
Federal Tax = 20% × $264
Federal Tax = $52.80
State Tax will be
State Tax = 6% × $264
State Tax = $15.84
Social Security will be
Social Security = 6.45% × $264.00
Social Security = $17.03
Total Deduction will be as
Total Deduction = Federal Tax + State Tax + Social Security
Total Deduction = $52.80 + $15.84 + $17.03
Total Deduction = $85.67
Net Pay = Gross Income - Total Deduction
Net Pay = $264.00- $85.67
Net Pay = $178.33
Learn more about tax on:
https://brainly.com/question/25783927
#SPJ1
A small box of muffins contains 2 blueberries, 1 cinnamon, and 3 chocolate. if a large batch of muffins contains 9 chocolate how many blue muffins are there?
PLS DO NOT JUST ADD THE ANSWER PLS ADD HOW U GOT IT TOO!!!
6th grade math
Answers
Answer: yo we have a problem
Step-by-step explanation:
im in 10th grade and i cant answer this problem 0.0
1) During the 1990s, the forested area Guatemala decreased at an Average Rate of 1.7%. The forested area on Guatemala was about 34,400 square Kilometers in 1990.
((Rest Picture))
2) From 1995 to 2005, the tuition at a college increased by about 7% per year. Tuition in 1995 was $12,000n

Answers
Answer:
A is correct answer
How to calculate this ?Here, we want to write an equation for a depreciation
The general form is;
V is the present value in 2005
I is the initial value in 1990 which is 34,400
r is the decrease rate which is 1.7/100 = 0.017
t is the difference in years which is 2005-1990 = 15
Substituting these values, we have
V = 34,400(1-0.017)^15
V = 22,407.65 km^2
To learn more about linear regression refers to
https://brainly.com/question/23268467
#SPJ1
solve the system of equations y=4x-3 and y=-2x+9 what is x and y will give brainliest
Answers
To solve the system of equations y=4x-3 and y=-2x+9, we can set the two equations equal to each other and solve for x:
4x - 3 = -2x + 9
Adding 2x and 3 to both sides, we get:
6x = 12
Dividing both sides by 6, we get:
x = 2
Now that we have the value of x, we can substitute it into either of the original equations to find the corresponding value of y. Let's use the first equation:
y = 4x - 3
y = 4(2) - 3
y = 8 - 3
y = 5
Therefore, the solution to the system of equations is x = 2 and y = 5. The solution is the ordered pair (2, 5).
The graph of y = f(x) is shown below. Determine the value of x when
f(x) = -2?

Answers
PLEASE HELP ME QUICK 40 POINTS
Find the missing side

Answers
The measure of the missing side length x in the right triangle is approximately 18.8 units.
What is the missing side length?The figure in the image is a right triangle.
Angle θ = 37 degrees
Adjacent to angle θ = 25 units
Opposite to angle θ = x
To solve for the missing side length x, we use the trigonometric ratio.
SOHCAHTOA
Note that: TOA → tangent = opposite / adjacent.
Hence:
tan( θ ) = opposite / adjacent
Plug in the values:
tan( 37 ) = x / 25
Solve for x by cross multiplying:
x = tan( 37 ) × 25
x = 18.838
x = 18.8 units
Therefore, the value of x is approximately 18.8.
Learn more about trigonometric ratio here: brainly.com/question/28016662
#SPJ1
Factorise each expression
a) 3x+12m
b) 6h²+18ah
Answers
After factorising the given expression we have the factors:
a) = 3(x + 4m)
b) = 6h(h + 3a)
What is factorising?Expanding brackets in reverse is a process known as factorising. Fully factorising an expression entails putting it in brackets by eliminating the factors with the highest common denominator.
The easiest method of factoring is:
Find the terms in the expression that have the highest common factor.Anytime there are any brackets, put the highest common factor (HCF) there.By multiplying out, fill in each term in the brackets.Factorisation:
a) 3x+12m
= 3(x + 4m)
b) 6h²+18ah
6h(h + 3a)
Thus, After factorising the given expression we have the factors:
a) = 3(x + 4m)
b) = 6h(h + 3a)
Learn more about factorising
https://brainly.com/question/20293447
#SPJ1
Select the TWO numbers that have a 4 in the thousandths place. *

Answers
Answer:
54,436.004 and 247,892.984
Step-by-step explanation:
Answer:
third and fourth
Step-by-step explanation:
if a retailer would like to estimate the proportion of their customers who bought an item after viewing their website on a certain day with a 90% confidence level and 5% margin of error, how many customers do they have to monitor? previous information has shown that 58% of users do this.
Answers
If customers bought an item after viewing their website on "certain-day" with 90% "confidence-level" and 5% "margin-of-error", then the number of customers they have to monitor is 264.
To estimate the proportion of customers who bought an item after viewing the retailer's website, the retailer needs to conduct a sample survey.
To determine the "sample-size" needed for the survey, we use the formula:
⇒ n = [Z² × p × (1 - p)]/E²,
where : n is = sample-size of customer,
Z is = z-score associated with confidence-level (90% confidence level corresponds to a z-score of 1.645),
p is = estimated proportion of customers who bought an item (in this case it is 58% = 0.58),
E is = margin-of-error (5% = 0.05),
Substituting the values,
We get,
⇒ n = [1.645² × 0.58 × (1 - 0.58)]/0.05²,
⇒ n = 263.67 ≈ 264,
Therefore, They have to monitor 264 customers.
Learn more about Confidence Level here
https://brainly.com/question/26962316
#SPJ4
what is 2x+10=38
if you answer correct i give brainlyest
Answers
Answer: X equals 14

Let $ABCD$ be a regular tetrahedron with side length 2. The plane parallel to edges $AB$ and $CD$ and lying halfway between them cuts $ABCD$ into two pieces. Find the surface area of one of these pieces.
Answers
The surface area of one of the pieces formed by the plane parallel to edges AB and CD and lying halfway between them in a regular tetrahedron with side length 2 is **4√3 square units**.
To find the surface area of one of the pieces, we need to calculate the area of the triangular face of the tetrahedron that is cut by the plane.
Since the tetrahedron is regular, all four triangular faces are congruent equilateral triangles. The side length of each triangular face is equal to the side length of the tetrahedron, which is given as 2 units.
To find the area of an equilateral triangle, we can use the formula A = (√3/4) * s^2, where A is the area and s is the side length. Plugging in s = 2 into the formula, we get A = (√3/4) * (2^2) = √3 square units.
Therefore, the surface area of one of the pieces is 4 times the area of the triangular face, which is 4 * √3 = 4√3 square units.
Know more about surface area here:
https://brainly.com/question/2835293
#SPJ11
if an indifference curve is straight (i.e., it doesn't "bow" inward), the marginal rate of substitution is always constant.
T/F
Answers
If an indifference curve is straight, the marginal rate of substitution (MRS) is indeed constant.
The MRS represents the rate at which a consumer is willing to exchange one good for another while maintaining the same level of satisfaction. A straight indifference curve means that the consumer is indifferent between two goods, regardless of the quantity of each good they have. Therefore, the MRS between these goods remains constant, regardless of the quantity of each good consumed. On the other hand, if an indifference curve is bowed inward, the MRS is not constant and changes as the consumer moves along the curve. Yes, if an indifference curve is straight and does not bow inward, it implies that the marginal rate of substitution (MRS) is constant. In this case, the consumer is willing to substitute one good for another at a fixed rate, regardless of the quantity of goods consumed. This constant MRS reflects the consumer's equal preference for both goods, and thus, the indifference curve remains linear.
To know more about MRS visit:
https://brainly.com/question/30763866
#S[PJ11
Write a function g whose graph represents the indicated transformation of the graph of f.
g(x)=____

Answers
Step-by-step explanation:
the simplest way to explain the transformation is a reflection across the x-axis and then a translation down by 4 units.
for the first (reflection across the x-axis) we only need to flip the sign (multiply by -1) of the functional result.
for the second we need them to subtract 4 from every functional value.
so, we get
g(x) = -f(x) - 4
y=1/4x + 8 what would be the slope and the y-intercept
Answers
Answer:
y= 1/4x + 8
comparing with
y= mx + c
slope = 1/4
for y intercept x=0
y=8
Step-by-step explanation:
The slope of the line is 1/4, The y-intercept is 8.
In the equation y = (1/4)x + 8, the coefficient of x is 1/4. This coefficient represents the slope of the line.
Therefore, the slope of the line is 1/4.
The equation is in the form y = mx + b, where m represents the slope and b represents the y-intercept.
In this equation, the y-intercept is the value of y when x is 0. By substituting x = 0 into the equation, find the y-intercept.
y = (1/4)(0) + 8
= 0 + 8
= 8
Hence, the y-intercept is 8.
To know more about line here
https://brainly.com/question/30003330
#SPJ6
What is the measure of circumscribed
O 45°
O 50°
O 90°
O 95°

Answers
The measure of the inscribed angle is equal to 90 degrees
What is an inscribed angleThe inscribed angle theorem mentions that the angle inscribed inside a circle is always half the measure of the central angle or the intercepted arc that shares the endpoints of the inscribed angle's sides. In a circle, the angle formed by two chords with the common endpoints of a circle is called an inscribed angle and the common endpoint is considered as the vertex of the angle.
In this problem, the side length of the square is 5 which forms 90 degrees to all the other sides.
The measure of the circumscribed angle is 90 degree
Learn more on inscribed angle here;
https://brainly.com/question/3538263
#SPJ1
Evaluate the indefinite integral. (Use C for the constant of integration.)
eu
∫(7 − eu)2du
integral.gif
Answers
The indefinite integral of (7 - eu)^2 du is 49u - 14(e^u)/1 + e^2u/2 + C.
The indefinite integral of (7 - eu)^2 du is:
∫(7 - eu)^2 du = ∫(49 - 14eu + e^2u) du = 49u - 14(e^u)/1 + e^2u/2 + C
To evaluate the indefinite integral of (7 - eu)^2 du, we use the formula for integrating powers of exponential functions, which states that ∫e^au du = (1/a)e^au + C, where C is the constant of integration. By applying this formula, we can expand the given expression and integrate term by term.
First, we expand (7 - eu)^2 using the binomial theorem, which gives us 49 - 14eu + e^2u. Then, we integrate each term using the formula above, which gives us 49u - 14(e^u)/1 + e^2u/2 + C, where C is the constant of integration.
Therefore, the indefinite integral of (7 - eu)^2 du is 49u - 14(e^u)/1 + e^2u/2 + C.
Learn more about indefinite integral here
https://brainly.com/question/27419605
#SPJ11
Alberto started out bench pressing 60 pounds. He then added 5 pounds every week. Determine whether the situation is linear or nonlinear, and proportional or nonproportional
Answers
Answer
linear
nonproportional
Step-by-step explanation:
Since for each equal change in time (1 week), there is an equal change in weight (5 lb), the situation is linear.
At time zero, the first week, the weight was not zero. It was 60 lb, so it is not proportional.
Answer:
linear
nonproportional
QUESTION 6-1 POINT
The probability that Lou is on time for a given dass is 75 percent. If there are 32 classes during the semester, what is the
best estimate of the number of times out of 32 that Lou is on time to class? Round your answer to the nearest integer,
Provide your answer below.
help me
Answers
To find the answer, we use the formula:
Number of times on time = Probability of being on time x Number of classes
Substituting the given values, we get:
Number of times on time = 0.75 x 32
Number of times on time = 24
Therefore, the best estimate of the number of times out of 32 that Lou is on time to class is 24.
What is the best estimate of the number of times out of 32 that Lou is on time to class if the probability of him being on time for a given class is 75%? To explain why we used the formula, we note that the problem provides us with the probability of Lou being on time to class for a given day, which is 0.75 or 75%. We are also given the number of classes during the semester, which is 32. To estimate the number of times Lou is on time out of 32 classes, we simply multiply the probability of being on time by the total number of classes. This gives us an expected value of 24 classes out of 32 where Lou is on time. This approach is based on the assumption that Lou's probability of being on time is independent across classes, which may or may not be true in practice.Learn more about Probability
brainly.com/question/30034780
#SPJ11
Jackson is working two summer jobs, making $10 per hour washing cars and $12 per hour landscaping. Last week jackson worked a total of 14 hours and earned a total of $152. Determine the number of hours jackson worked washing cars last week and the number of hours he worked landscaping last week.
Answers
The number of hours Jackson worked washing cars is 8 hours and the number of hours he worked landscaping is 6 hours
The payment of car washing per hour = $10
The payment for landscaping = $12
Total number of hours worked = 14 hours
Number of hours worked in car washing = x
Number of hours worked in landscaping = y
Then the first equation will be
x + y = 14
x = 14 - y
Total amount he earned = $152
Next equation will be
10x + 12y = 152
Here we have to use substitution method
10(14-y) + 12y = 152
140 - 10y +12y = 152
140 + 2y = 152
2y = 152 - 140
2y = 12
y = 12/2
y = 6 hours
Then
x = 14 - y
x = 14 -6
x = 8 hours
Hence, the number of hours Jackson worked washing cars is 8 hours and the number of hours he worked landscaping is 6 hours
Learn more about substitution method here
brainly.com/question/14619835
#SPJ1
eacher: ""the first triangle is an isosceles triangle. the second triangle is an isosceles triangle. the third triangle is not an isosceles triangle. based on your observations alone what should be the definition of an isosceles triangle?""what does this question illustrate about the geometry teacher’s questioning techniques?
Answers
We have demonstrated the definition of an isosceles triangle.
What is an isosceles triangle?
An isosceles triangle is a triangle with at least two equal-length sides in geometry. It is sometimes specified as having exactly two equal-length sides, and sometimes as having at least two equal-length sides, with the latter version including the equilateral triangle as a special case.
The isosceles triangle has both two equal sides and two equal angles. The name derives from the Greek iso (same) and Skelos (leg). A triangle with all sides equal is called an equilateral triangle, and a triangle with no sides equal is called a scalene triangle.
The given diagram shows an isosceles triangle.
Hence, we have demonstrated the definition of an isosceles triangle.
To learn more about an isosceles triangle, visit:
https://brainly.com/question/1475130
#SPJ4

a rectangle has a height of 222 and a width of 5x^2-2x 35x 2 −2x 35, x, squared, minus, 2, x, plus, 3.
Answers
The area of the rectangle with a height of 222 and a width of 5x^2 - 2x + 35 is given by the expression 1110x^2 - 444x + 7770.
The rectangle has a height of 222 and a width of 5x^2 - 2x + 35.
To find the area of the rectangle, we multiply the height by the width. Let's substitute the given values:
Area = height * width
Area = 222 * (5x^2 - 2x + 35)
To simplify the expression, we can distribute the 222 to each term within the parentheses:
Area = 222 * 5x^2 - 222 * 2x + 222 * 35
Now, let's further simplify each term:
Area = 1110x^2 - 444x + 7770
Therefore, the area of the rectangle with a height of 222 and a width of 5x^2 - 2x + 35 is given by the expression 1110x^2 - 444x + 7770.
Learn more about rectangle here
https://brainly.com/question/25292087
#SPJ11
What is the sum of -4/5 and -3/5
Answers
Answer:
-7/5
Step-by-step explanation:
It is given that,
→ (-4/5) + (-3/5) = ?
Let's solve the problem,
→ (-4/5) + (-3/5)
→ (-4/5) - (3/5)
→ (-4 - 3)/5 = -7/5
Thus, the answer is -7/5.