Suppose a homogeneous system of equations has 13 variables and 8 equations. How many solutions will it have
Answers
The number of solutions that a homogeneous system of equations with 13 variables and 8 equations will have depends on the rank of the coefficient matrix.
If the rank of the coefficient matrix is less than the number of variables (13), then the system will have infinitely many solutions.
If the rank is equal to the number of variables, then the system will have a unique solution. If the rank is less than the number of variables but greater than the number of equations (8), then the system will have a nontrivial solution.
It is not possible to determine the rank of the coefficient matrix or the number of solutions without actually solving the system or knowing more information about the specific equations involved.
for such more question on word problem
https://brainly.com/question/1781657
#SPJ11
Related Questions
If two angles are supplementary and one of the angles measures 62°, what is the measure of the other angle?
Answers
Answer:118 for the other angle
Step-by-step explanation:trust me bro
On the provided grid, label and scale the axes and groan this situation with M on the vertical axis and R on the horizontal axis. Make sure the scale is large enough to see how much they would raise if they sell 1000 tickets.
Answers
On solving the provided question, we can say that the money they would raise if they sell 1000 tickets will be given the equation that is y = 24R/10
What is equation?A mathematical equation is a formula that joins two statements and uses the equal symbol (=) to indicate equality. A mathematical statement that establishes the equality of two mathematical expressions is known as an equation in algebra. For instance, in the equation 3x + 5 = 14, the equal sign places the variables 3x + 5 and 14 apart. The relationship between the two sentences on either side of a letter is described by a mathematical formula. Often, there is only one variable, which also serves as the symbol. for instance, 2x – 4 = 2.
the money they would raise if they sell 1000 tickets
will be given the equation that is
M = 24/10R
y = 24R/10
To know more about equation visit:
https://brainly.com/question/649785
#SPJ1
In the equation 6x-2=-4x 2 spencer claims that the first step is to add 4x to both sides
Answers
yes, for your x to be positive and to make it remain on the left hand side you actually have to add 4x to both side to eliminate x from the right hand side.
Which of the following are equivalent to the function y = 3cOS X + 2? Check all that apply. A. y = 3cos(-x) + 2 B. y = -3cOS X-2 C. y = 3sin(x + 1) +2 + D. y = 3sin(x-7)+2

Answers
We need to plot the graphs of these functions on the same axis:
\(\begin{gathered} \text{From the graph, we s}e\text{ the function} \\ y\text{ = 3cosx + 2 has the same grap as } \\ y\text{ = 3sin(x + }\frac{\pi}{2})\text{ + 2} \\ \\ \text{Please note from angles in trigonometry:} \\ \sin \text{ (90 + }\theta)\text{ = cos }\theta \\ \cos x\text{ = sin (90 + x)} \end{gathered}\)Hence, the correct option
\(y\text{ = 3sin(x + }\frac{\pi}{2})\text{ + 2 (option }C)\)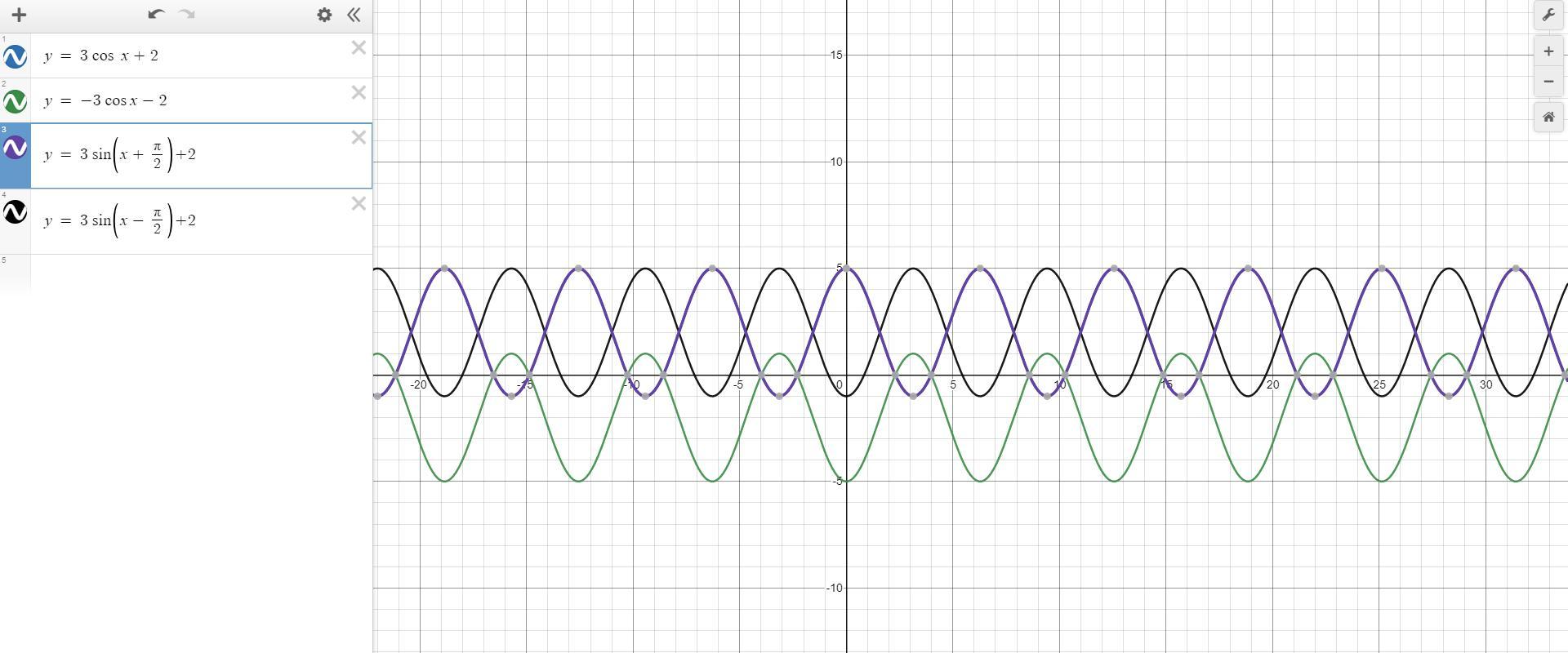

traffic engineers in florida want to reduce the rate of accidents between pedestrians and cars at intersections. research has shown that replacing stoplights with roundabouts (also called traffic circles) can improve safety for bikers and pedestrians. engineers wanted to test this concept so it can be applied across florida, and last year, they replaced five timed stoplights in a florida city with roundabouts. the accident rates at five intersections before the intervention were 5.1, 3.4, 6.1, 4.9, and 4.1 accidents per month. after installing roundabouts, the new rates of pedestrian accidents were 4.5, 3.6, 5.5, 4.8, and 4.1 accidents per month. does replacing stoplights with roundabouts significantly reduce the rate of accidents at intersections? use an alpha value of 0.05 in your decision.
Answers
Replacing stoplights with roundabouts does not significantly reduce the rate of accidents at intersections based on the given data.
Based on the statistical analysis, replacing stoplights with roundabouts does not significantly reduce the rate of accidents at intersections.
To test this hypothesis, we will use a paired t-test, which compares the means of two sets of paired data. The null hypothesis is that there is no significant difference between the mean accident rates before and after installing roundabouts, while the alternative hypothesis is that the mean accident rate after installing roundabouts is significantly lower than before.
Here are the steps to conduct the paired t-test:
Calculate the difference between the accident rates before and after installing roundabouts for each intersection.Calculate the mean and standard deviation of the differences.Calculate the t-value using the formula: t = (mean of the differences) / (standard deviation of the differences / sqrt(n)), where n is the number of paired observations.Calculate the degrees of freedom using the formula: df = n - 1.Find the critical t-value at a 0.05 level of significance and df from a t-distribution table.Compare the calculated t-value with the critical t-value. If the calculated t-value is greater than the critical t-value, reject the null hypothesis. If the calculated t-value is less than or equal to the critical t-value, fail to reject the null hypothesis.Using the given data, the differences between the accident rates before and after installing roundabouts are:
-0.6, 0.2, 0.6, -0.1, 0
The mean of the differences is 0.02, and the standard deviation is 0.43. There are 5 paired observations, so the degrees of freedom are 4.
Using the formula, we get:
t = 0.02 / (0.43 / √(5)) = 0.14
The critical t-value at a 0.05 level of significance and 4 degrees of freedom is 2.776 from a t-distribution table.
Since the calculated t-value (0.14) is less than the critical t-value (2.776), we fail to reject the null hypothesis. Therefore, we can conclude that replacing stoplights with roundabouts does not significantly reduce the rate of accidents at intersections based on the given data.
Learn more about the null hypothesis
https://brainly.com/question/25263462
#SPJ4
BRAINLIEST,
PLZ HELP
the function f(x) is given by
f(x)= 3x-1
find it's simplest form
a. f^-1 f(x)
b.ff(x)
Answers
f(x) = 3x - 1
a) let y = f(x)
y = 3x - 1
solve for x
3x = y + 1
x = (y+1) / 3
interchange x's and y's
y = (x+1) / 3
f inverse = (x+1) / 3
b) f inverse of f(x) = (3x-1+1) / 3
f inverse of f(x) = 3x / 3
f inverse of f(x) = x
Identify all of the root(s) of g(x) = (x2 3x - 4)(x2 - 4x 29). -1 1 -4 4 2 5i 2 - 5i -2 10i -2 - 10i
Answers
The roots are (x + 1), (x - 4), (2 + 5i), and (2 - 5i).
g(x) = (x2 - 3x - 4)(x2 - 4x + 29)
Let us first consider x^2 - 3x - 4
By splitting the middle term
= x^2 + 1x - 4x - 4
= x(x + 1) - 4(x + 1)
= (x + 1)(x - 4)
Now let us consider x^2 - 4x + 29
First group the terms with variable on LHS and move the constant on the other side
x^2 - 4x = -29
Add 4 on both sides
x^2 - 4x + 4 = -29 + 4
x^2 - 4x + 4 = -25
It can be written as perfect squares
(x - 2)^2 = -25
We know that
i =√1
Take square root on both sides
x - 2 = ± 5i
x = 2 ± 5i
So we get,
x = 2 + 5i and x = 2 - 5i
g(x) = (x + 1)(x - 4)(2 + 5i)(2 - 5i)
A square root of a number is a price that, whilst extended by means of itself, offers variety. instance: four × four = 16, so a square root of 16 is four. The word that (−four) × (−four) = 16 too, so −four is likewise a square root of sixteen. The symbol is √ usually way the wonderful rectangular root. example: √36 = 6 (because 6 x 6 = 36).
Learn more about the square roots here https://brainly.com/question/3617398
#SPJ4
Suppose that y₁ (t) is solution of L(y1) = 0 and y2 (t) is solution of L(y2) b(t) = 0, where L(y) = 2y+3y + 4y. Choose all the statements below that are correct. The function 2 y1 is a solution of the non-homogeneous equation L(y) = 2b(t). The function Y₁ + y2 is solution of the homogenous equation L(y) = 0. The function 7 y₁ - 7y2 is solution of the homogenous equation L(y) = 0 The function 2 y2 is a solution of the non-homogeneous equation L(y) = 2b(t). The function 3 y₁ is solution of the homogenous equation L(y) = 0. The function 2 y₁ is a solution of the non-homogeneous equation L(y) = 2b(t). The function Y₁ + y2 is solution of the homogenous equation L(y) = 0. The function 7 y1 - 7y2 is solution of the homogenous equation L(y) = 0 The function 2 y2 is a solution of the non-homogeneous equation L(y) = 2b(t). The function 3y₁ is solution of the homogenous equation L(y) = 0. The function 7y₁ + y2 is solution of the non-homogenous equation L(y) = b. The function 3 y2 is solution of the non-homogenous equation L(y) = b. The function Y1 Y2 is solution of the non-homogenous equation L(y) = -b
Answers
The correct statements of these functions are:
The function 2y₁ is a solution of the non-homogeneous equation L(y) = 2b(t).The function y₁ + y₂ is a solution of the homogeneous equation L(y) = 0.The function 7y₁ - 7y₂ is a solution of the homogeneous equation L(y) = 0.The function 3y₁ is a solution of the homogeneous equation L(y) = 0.Let's go through each statement and determine its correctness:
1. The function 2y₁ is a solution of the non-homogeneous equation L(y) = 2b(t).
This statement is correct. If y₁ is a solution of L(y) = 0, then multiplying it by 2 gives 2y₁, which is a solution of L(y) = 2b(t) (non-homogeneous equation).
2. The function y₁ + y₂ is a solution of the homogeneous equation L(y) = 0.
This statement is correct. Since both y₁ and y₂ are solutions of L(y) = 0 (homogeneous equation), their sum y₁ + y₂ will also be a solution of L(y) = 0.
3. The function 7y₁ - 7y₂ is a solution of the homogeneous equation L(y) = 0.
This statement is correct. Similar to statement 2, since both y₁ and y₂ are solutions of L(y) = 0, their difference 7y₁ - 7y₂ will also be a solution of L(y) = 0.
4. The function 2y₂ is a solution of the non-homogeneous equation L(y) = 2b(t).
This statement is incorrect. Multiplying y₂ by 2 does not make it a solution of the non-homogeneous equation L(y) = 2b(t).
5. The function 3y₁ is a solution of the homogeneous equation L(y) = 0.
This statement is correct. If y₁ is a solution of L(y) = 0, then multiplying it by 3 gives 3y₁, which is still a solution of L(y) = 0 (homogeneous equation).
6. The function 7y₁ + y₂ is a solution of the non-homogeneous equation L(y) = b.
This statement is incorrect. The function 7y₁ + y₂ is a linear combination of two solutions of the homogeneous equation L(y) = 0, so it cannot be a solution of the non-homogeneous equation L(y) = b.
7. The function 3y₂ is a solution of the non-homogeneous equation L(y) = b.
This statement is incorrect. The function 3y₂ is a linear combination of y₂, which is a solution of L(y) = 0 (homogeneous equation), so it cannot be a solution of the non-homogeneous equation L(y) = b.
8. The function y₁y₂ is a solution of the non-homogeneous equation L(y) = -b.
This statement is incorrect. The function y₁y₂ is a product of two solutions of the homogeneous equation L(y) = 0, so it cannot be a solution of the non-homogeneous equation L(y) = -b.
To summarize, the correct statements are:
The function 2y₁ is a solution of the non-homogeneous equation L(y) = 2b(t).
The function y₁ + y₂ is a solution of the homogeneous equation L(y) = 0.
The function 7y₁ - 7y₂ is a solution of the homogeneous equation L(y) = 0.
The function 3y₁ is a solution of the homogeneous equation L(y) = 0.
Learn more about functions
https://brainly.com/question/31062578
#SPJ11
The correct statements are:
1. The function 2y₁ is a solution of the non-homogeneous equation L(y) = 2b(t).
2. The function Y₁ + y₂ is a solution of the homogeneous equation L(y) = 0.
3. The function 7y₁ - 7y₂ is a solution of the homogeneous equation L(y) = 0.
4. The function 2y₂ is a solution of the non-homogeneous equation L(y) = 2b(t).
5. The function 3y₁ is a solution of the homogeneous equation L(y) = 0.
How to determine the correct statementsThe remaining statements are incorrect:
1. The statement "The function 2y₁ is a solution of the non-homogeneous equation L(y) = 2b(t)" is already mentioned above and is correct.
2. The statement "The function Y₁ + y₂ is a solution of the homogeneous equation L(y) = 0" is correct.
3. The statement "The function 7y₁ - 7y₂ is a solution of the homogeneous equation L(y) = 0" is correct.
4. The statement "The function 2y₂ is a solution of the non-homogeneous equation L(y) = 2b(t)" is correct.
5. The statement "The function 3y₁ is a solution of the homogeneous equation L(y) = 0" is correct.
6. The statement "The function 7y₁ + y₂ is a solution of the non-homogeneous equation L(y) = b" is incorrect because the non-homogeneous term should be 2b(t) according to the given information.
7. The statement "The function 3y₂ is a solution of the non-homogeneous equation L(y) = b" is incorrect because the non-homogeneous term should be 2b(t) according to the given information.
8. The statement "The function Y₁Y₂ is a solution of the non-homogeneous equation L(y) = -b" is incorrect because the non-homogeneous term should be 2b(t) according to the given information.
Therefore, the correct statements are 1, 2, 3, 4, and 5.
Learn more about functions at https://brainly.com/question/11624077
#SPJ4
Complete the inequality with >, <,>,<,is greater than, comma, is less than, comma or ==equals. 2^52 5 2, start superscript, 5, end superscript 5^25 2 5, squared
Answers
Answer:
\(2^5 > 5^2\)
Step-by-step explanation:
Given the expression \(2^5 \ 5^2\), we are to complete the inequality by inserting the correct inequality signs in between the values.
Before we do that, we must know the value of each indicinal expressions.
\(2^5 = 2*2*2*2*2\\\\2^5 = 4*4*2\\\\2^5 = 16*2\\\\2^5 = 32\)
Also,
\(5^{2} = 5*5\\\\5^2 = 25\)
From the values gotten, we can clearly see that 32 is greater than 25. This means that 2⁵ is greater than 5². Hence the inequality sign that will complete the expression is a greater than sign (>).
The inequality will be \(2^5 > 5^2\)
Answer:
its this
over here...

The domain of y = x2 is The range of y = x2 is
Answers
Answer:
The domain is: (-∞,∞)
The range is: (0,∞)
Step-by-step explanation:
Answer:
The domain of y = x2 is
✔ all real numbers
The range of y = x2 is
✔ y >= 0
Step-by-step explanation: Hope this helps!
what is the volume of this figure?help asap!!!!!

Answers
Answer:
50
Step-by-step explanation:
Answer:
vol. = 875 ft³Step-by-step explanation:
you to divide the figure into 3 parts (see attached image)
volume = L*W*H
where:
L = 5 ft
W = 5 ft.
H = 10 + 15 + 10 = 35 ft.
plug in values into the formula:
vol. = 5 x 5 x 35
vol. = 875 ft³

solve pls brainliest

Answers
Answer:
48.95
Step-by-step explanation:
I AM SO THANKFUL IF YOU HELP MEE!!!

Answers
Answer:
Step-by-step explanation:
i think its D
A concession stand charges $6 for popcorn and $8 for a hotdog. They made $100 in one night and sold 10 bags of popcorn. How many hotdogs did they sell?
Answers
Answer:
They sold 5 hotdogs.
Step-by-step explanation:
Answer:
5
Step-by-step explanation:
10 bags of popcorn would equal 60 dollars. That would leave 40 dollars. So 40 divided by 8 is 5
How is the product of 2 and-5 shown on a number line
Answers
Answer:
-10
Step-by-step explanation:
start at 0 and move backwards 5(gives you -5) then move backwards 5 more(-10)
1600 ÷ 4 equals 400 which number is the divisor
Answers
which of the following is the correct factorial notation for dr. elder’s new study?
Answers
Factorial notation is used to represent the product of a series of descending positive integers, and is denoted by an exclamation mark.
For example, 5! represents 5 x 4 x 3 x 2 x 1, which equals 120. If the study involves counting the number of ways a certain group of items can be arranged, factorial notation may be used to express the total number of possible arrangements. However, without knowing the specifics of Dr. Elder's study, it is impossible to provide the correct factorial notation. Therefore, I would recommend providing more details about the study in order to receive a more accurate answer.
To know more about factorial notation visit:
https://brainly.com/question/31876029
#SPJ11
a farmer can buy two types of plant​ food, mix a and mix b. each cubic yard of mix a contains pounds of phosphoric​ acid, pounds of​ nitrogen, and pounds of potash. each cubic yard of mix b contains pounds of phosphoric​ acid, pounds of​ nitrogen, and pounds of potash. the minimum monthly requirements are pounds of phosphoric​ acid, pounds of​ nitrogen, and pounds of potash. if mix a costs ​$ per cubic yard and mix b costs ​$ per cubic​ yard, how many cubic yards of each mix should the farmer blend to meet the minimum monthly requirements at a minimum​ cost? what is this​ cost?
Answers
To solve this problem, we need to set up a system of equations based on the given information. Let's assume that the farmer needs x cubic yards of mix a and y cubic yards of mix b.
For phosphoric acid, the equation would be:
x * pounds of phosphoric acid in mix a + y * pounds of phosphoric acid in mix b = pounds of phosphoric acid required
For nitrogen, the equation would be:
x * pounds of nitrogen in mix a + y * pounds of nitrogen in mix b = pounds of nitrogen required
For potash, the equation would be:
x * pounds of potash in mix a + y * pounds of potash in mix b = pounds of potash required
We can solve this system of equations using substitution or elimination method. Once we find the values of x and y, we can calculate the total cost.
Since the question asks for the answer in more than 100 words, I'll provide an explanation for the solution process.
1. Set up the equations using the given information.
2. Solve the system of equations to find the values of x and y.
3. Substitute the values of x and y into the cost equation to find the total cost.
The solution to the problem is to blend x cubic yards of mix a and y cubic yards of mix b to meet the minimum monthly requirements at a minimum cost. The total cost can be calculated by substituting the values of x and y into the cost equation.
To know more about equations visit
https://brainly.com/question/14686792
#SPJ11
A train travels 60 km in 1 hour. How long will it take to go 150 km, if the speed is uniform
Answers
Answer:
2.5 hour for 150 kilometers
a rectangular rug covers 1200 square inches on the floor. The length of the rug is 30 inches .What is the length in inches of the rug
Answers
Answer:
The length is 30 (which you aready said) and the width is 40
Step-by-step explanation:
1200/30=40
(another way)
120/30=4 (multiply each side by ten)
Finding the side length of a cube from its Volume in liters A technical machinist is asked to build a cubical steel tank that will hold 275 L of water. Calculate in meters the smallest possible inside length of the tank. Round your answer to the nearest 0.001 m. X 5 ?
Answers
The smallest possible inside length of the cubical steel tank that can hold 275 liters of water is approximately 0.640 meters.
The side length of the cube is found by converting the volume of water from liters to cubic meters, as the unit of measurement for the side length is meters.
Given that the volume of water is 275 liters, we convert it to cubic meters by dividing it by 1000 (1 cubic meter = 1000 liters):
275 liters / 1000 = 0.275 cubic meters
Since a cube has equal side lengths, we find the side length by taking the cube root of the volume. In this case, we find the cube root of 0.275 cubic meters:
∛(0.275) ≈ 0.640
Rounded to the nearest 0.001 meters, the smallest possible inside length of the tank is approximately 0.640 meters.
To know more about smallest possible inside length, refer to the link :
https://brainly.com/question/17304098#
#SPJ11
Find the missing side lengths. Leave your answer as radicals in simplest form.

Answers
The values of the sides are;
41. x = 18√3. Option D
42. x = 6√3. Option A
How to determine the valuesUsing the different trigonometric identities, we have;
41. Using the tangent identity, we have;
tan 60 = 9√2/y
cross multiply the values
y =9√2 ×√3
y = 9√6
Using the sine identity;
sin 45 = y/x
1/√2 = 9√6/x
cross multiply the values, we have;
x = 9√2 ×√3 ×√2
x = 18√3
42. Using the cosine identity
cos 60 = 3√3 /x
cross multiply, we have;
x = 6√3
Learn more about trigonometric identities at: https://brainly.com/question/7331447
#SPJ1
need some help with this

Answers
Answer:
the slope is 1
Step-by-step explanation:
Answer:
slope = 1
Step-by-step explanation:
Calculate the slope m using the slope formula
m = \(\frac{y_{2}-y_{1} }{x_{2}-x_{1} }\)
with (x₁, y₁ ) = (- 1, 4) and (x₂, y₂ ) = (4, 9)
m = \(\frac{9-4}{4-(-1)}\) = \(\frac{5}{4+1}\) = \(\frac{5}{5}\) = 1
Which statements below are TRUE?
I. To “undo” division, you must do the inverse operation, which is subtraction.
II. The inverse operation of multiplication is division
III. An equation is two equivalent expressions.
IV. When solving an equation, the goal is to determine the value of the coefficient.
Answers
Can someone please help?

Answers
Answer: C = 40
A = 100
Step-by-step explanation:
Answer:
40
Step-by-step explanation:
one thing rsLtd do I FTC Ted e. xrtd dt
I NEED ASAPP ILL MAKE YOU BRAINLIEST ANSWERRR
Determine the intercepts of the line.
X-intercept: ( , )
y-intercept: ( , )

Answers
Answer:
x-int (-250, 0)
y-int (0, 100)
General Formulas and Concepts:
Algebra
The x-intercept is the x value when y = 0. Another way to reword that is when the graph crosses the x-axis. The y-intercept is the y value when x = 0. Another way to reword that is when the graph crosses the y-axis.Step-by-step explanation:
According the the line on the graph, we see that our x-intercept occurs when x = -250. We also see that our y-intercept occurs at y = 100.
x-int (-250, 0)
y-int (0, 100)
Answer:
X-intercept: (-250,0) and Y-intercept: (0,100)
Step-by-step explanation:
The x-intercept is where the line goes through the x line and the y-intercept is where the line goes through the y line. Please mark me brainliest. Also I hope it helped!
Least Value {15, 12, 21, 18, 25, 11, 17, 19, 20}
Answers
Answer:
11
Step-by-step explanation:
The number with the last value in this data set is 11. All the other numbers are greater than it in terms of numerical value. Imagine if all the numbers were represented through pennies. 11 would have the least amount of pennies.
What is the FV of $100 invested at 7% for one year (simple interest)? O $107 O $170 O$10.70 $10.07 k
Answers
The FV is $107 for the simple interest.
The formula to calculate simple interest is given as:
I = P × R × T
Where,I is the simple interest, P is the principal or initial amount, R is the rate of interest per annum, T is the time duration.
Formula to find FV:
FV = P + I = P + (P × R × T)
where,P is the principal amount, R is the rate of interest, T is the time duration, FV is the future value.
Given that P = $100, R = 7%, and T = 1 year, we can find the FV of the investment:
FV = 100 + (100 × 7% × 1) = 100 + 7 = $107
Therefore, the FV of $100 invested at 7% for one year (simple interest) is $107.
#SPJ11
Let us know more about FV : https://brainly.com/question/27941044.
use the trapezoidal rule, the midpoint rule, and simpson's rule to approximate the given integral with the specified value of n. (round your answers to six decimal places.) 3 0 1 10 y5 dy, n
Answers
Therefore, the degree of the resulting polynomial is m + n when two polynomials of degree m and n are multiplied together.
What is polynomial?
A polynomial is a mathematical expression consisting of variables and coefficients, which involves only the operations of addition, subtraction, multiplication, and non-negative integer exponents. Polynomials can have one or more variables and can be of different degrees, which is the highest power of the variable in the polynomial.
Here,
When two polynomials are multiplied, the degree of the resulting polynomial is the sum of the degrees of the original polynomials. In other words, if the degree of the first polynomial is m and the degree of the second polynomial is n, then the degree of their product is m + n.
This can be understood by looking at the product of two terms in each polynomial. Each term in the first polynomial will multiply each term in the second polynomial, so the degree of the resulting term will be the sum of the degrees of the two terms. Since each term in each polynomial has a degree equal to the degree of the polynomial itself, the degree of the resulting term will be the sum of the degrees of the two polynomials, which is m + n.
To know more about polynomials,
brainly.com/question/11536910
#SPJ1
what are the minimum and maximum numbers of elements in a heap of height h?
Answers
In a heap, the height is defined as the number of edges on the longest path from the root to a leaf node. The height of a heap with n elements is at most log₂(n+1).
To find the minimum and maximum numbers of elements in a heap of height h, we can use the formula:
The minimum number of elements in a heap of height h is 2^h (a complete binary tree of height h with the minimum number of nodes).
The maximum number of elements in a heap of height h is 2^(h+1) - 1 (a complete binary tree of height h with the maximum number of nodes).
Therefore, the minimum and maximum numbers of elements in a heap of height h are:
Minimum: 2^h
Maximum: 2^(h+1) - 1
Note that not all values of h are valid heap heights. A heap must be a complete binary tree, so its height can only take on values that satisfy the formula: \(h < = log₂(n+1),\)where n is the number of elements in the heap.
Learn more about height here:
https://brainly.com/question/10726356
#SPJ11